Russian Journal of Earth Sciences
Vol 1, No. 1, July 1998
Translated December 1998
On the effects of the inertia ellipsoid triaxiality in the theory
of nutation
S. M. Molodensky
Joint Institute of the Physics of the Earth, 10 Bolshaja Gruzinskaja,
Moscow 123810
Contents
Abstract
Modern nutation theories of the Earth and planets use the assumption, that the planetís
inertia
ellipsoid is symmetrical about the axes of rotation. Below we estimate the effects
of the inertia
ellipsoid triaxiality accurate to
((B-A)/(C-A))4, where
A, B, C are equatorial and polar principal
moments of inertia, respectively.
1. Introduction
As known, the nutational motion of the Earth and planets in space is fully determined
by
Euler angles
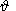 E, fE,
yE, which describe the position
of the body-fixed (Tesserand's) axes ( x, y, z ) with
respect to an immobile reference frame. At the same time, dynamic equations of motion
of an actual
planet model define only the components
(wx,
wy,
wz) of the angular velocity
vector
w with respect
to a moving reference frame. In the case of an axially symmetrical planet (equatorial
moments of
inertia satisfy the condition
A = B ) the Euler angles are connected with these components through
well-known Poinsot's formulae (see, for example, [Landau and Lifshitz, 1964]), but in the case
A
E, fE,
yE, which describe the position
of the body-fixed (Tesserand's) axes ( x, y, z ) with
respect to an immobile reference frame. At the same time, dynamic equations of motion
of an actual
planet model define only the components
(wx,
wy,
wz) of the angular velocity
vector
w with respect
to a moving reference frame. In the case of an axially symmetrical planet (equatorial
moments of
inertia satisfy the condition
A = B ) the Euler angles are connected with these components through
well-known Poinsot's formulae (see, for example, [Landau and Lifshitz, 1964]), but in the case
A 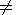 B Euler's relations between
B Euler's relations between
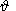 E, fE,
yE and
(wx, wy,
wz) present a rather complicated
(nonlinear)
system of ordinary differential equations which has not been investigated in all
details as yet.
E, fE,
yE and
(wx, wy,
wz) present a rather complicated
(nonlinear)
system of ordinary differential equations which has not been investigated in all
details as yet.
As was shown by Zharkov et al. [1996], in the case of
small violation of the
axial symmetry (if the parameter
h = (A-B)/(C-A)
satisfies the condition
|h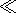 1| ) Euler's
equations can be solved by using the
perturbation method in
powers of this parameter; in such an approach, first-order (in
h ) corrections describe
only short-period (semidiurnal) perturbations of the values
1| ) Euler's
equations can be solved by using the
perturbation method in
powers of this parameter; in such an approach, first-order (in
h ) corrections describe
only short-period (semidiurnal) perturbations of the values
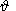 E,
fE,
yE. Nevertheless, this result
cannot be considered as a final solution of the problem under consideration, because
second-order corrections of
the order of
h2 can contain also long-period terms,
which perturb not only instant
values of the nutational amplitudes, but also their mean values. Modern VLBI measurements
are
most sensible just to these terms, and their analysis is most interesting for any
practical
purposes. Below we present a simple analytical expression that describes these corrections
with the accuracy of the order of
h4.
E,
fE,
yE. Nevertheless, this result
cannot be considered as a final solution of the problem under consideration, because
second-order corrections of
the order of
h2 can contain also long-period terms,
which perturb not only instant
values of the nutational amplitudes, but also their mean values. Modern VLBI measurements
are
most sensible just to these terms, and their analysis is most interesting for any
practical
purposes. Below we present a simple analytical expression that describes these corrections
with the accuracy of the order of
h4.
2. Statement of the Problem
As mentioned above, modern astrometric measurements determine the motion of fixed
points
of a planetary surface
R with respect to an immobile reference frame
usually connected with extragalactic objects. At the same time, well-known
Liouville's equation
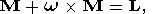 | (1) |
(where
w is the angular velocity of the Tesserand's
reference frame
(x, y, z),
M is the angular momentum of the planet,
L is the torque of external forces,
and the dot above symbol denotes the
time derivative) determines only the motion of the vector with respect to the moving
system
of coordinates
(x, y, z). To express the components of the vector
R in terms of the
known values
(wx, wy,
wz),
it is convenient to use the well-known Poinsot's kinematic relations (see, for example,
[Zharkov et al., 1996]) which connect the trajectory of
the vector
w with
respect to the moving reference frame
(x, y, z) (polhode) and the trajectory of the same
vector in space (herpolhode).
In the case of an axially symmetrical rigid planet (A=Bā and the products of inertia
Iik vanish), the components
M and
w are connected by the
well-known relation
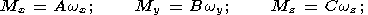 | (2) |
and the torque
L may be represented in the form
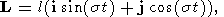 | (3) |
where
i,
j are unit vectors oriented along the axes
x and
y, respectively,
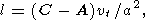 | (4) |
vt is the amplitude of the nearly diurnal tidal potential,
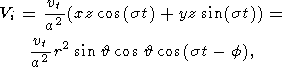 | (5) |
† is the mean radius of the planet,
(r, 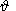 , f )
are spherical coordinates, and
s is tidal frequency.
, f )
are spherical coordinates, and
s is tidal frequency.
In the most general case, Liouville equation (1) represents a system of three nonlinear
ordinary differential equations with respect to three unknown functions
wx(t), wy(t),
wz(t). In the
case
h = 0, it has a very simple exact solution. In
fact, substituting (2)-(4) into (1), we obtain
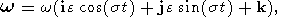 | (6) |
where
k is a unit vector that coincides with the
z axis and
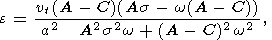 | (7) |
is the amplitude of nutational motion with respect to the moving reference frame
(x, y, z).
The fact that the amplitudes the
x and
y components of vector
w in (6)
are equivalent is a direct consequence of the axial symmetry of the problem under
consideration. In view of this, the
surfaces of polhode and herpolhode are exactly conical; in accordance with Poinsot's
kinematic
relations, the ratio of apex angles of these cones is defined by the relation
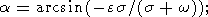 | (8) |
the amplitude of nutational motion of a vector
R in the body-fixed reference frame
(x, y, z) is equal to
a + e in the
case of prograde nutational motion (if the directions of the
w motion and
nutation coincide) and to in the opposite case of retrograde motion.
At
h = 0 the solutions of dynamic and kinematic nonlinear
equations can be
rather complicated. Because long-period perturbations are most important in practical
applications, below we use the method of its approximate solution based on the following
procedure:
- Dynamic equations (1) provide expressions for the components
wx(t),
wy(t),
wz(t) of the vector
w with respect to the moving reference
frame,
in which the effects of the inertia ellipsoid triaxiality are taken into account;
- Inverting Euler's kinematic relations between the known components
wx(t), wy(t),
wz(t) of the vector
w in the moving reference frame, the components
w1(t),
w2(t),
w3(t) of the same vector in
space,
and Euler's angles
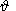 E, fE,
yE, these angles
can be expressed in terms of
wx(t), wy(t),
wz(t).
Taking into account, that the kinematic
relations are nonlinear, we use the first-order method of perturbations with respect
to the small parameter
h.
E, fE,
yE, these angles
can be expressed in terms of
wx(t), wy(t),
wz(t).
Taking into account, that the kinematic
relations are nonlinear, we use the first-order method of perturbations with respect
to the small parameter
h.
- To connect short-period first-order perturbations of the functions
w1(t), w2(t),
w3(t) and long-period second-order
perturbations of the same
functions, we use the well-known Poinsot's theorem stating that the rotation
of an arbitrary triaxial rigid body may be represented as the rolling of the
polhode over the herpolhode without sliding. In accordance with this theorem,
the ratio of trajectory lengths of the vector
w in the moving and
fixed reference frames
L1 and
L2 is equal to the ratio of the corresponding
periods. The perturbation of the trajectory
L2 in turn consists of (1) the known
terms which describe semidiurnal oscillations and (2) unknown terms of higher
orders of smallness which describe the mean radius of this trajectory. As is shown
below, this permits the mean radius of the trajectory
L2 to be found with
sufficient accuracy (of the order of
h4 ).
3. Tidal Torque for a Triaxial Body
Using expression (5) for the components of tidal potential in Cartesian
coordinates, it is easy to find the tidal torques which act on an axially
nonsymmetrical planet
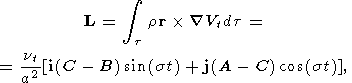 | (9) |
where
t is the total volume of the Earth. Replacing
the relation
between
wy and
My in equations (2) by the formula
My = Bwy
and then substituting (2) and (9) in Liouville's equation (1),
we obtain
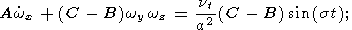 | (10a) |
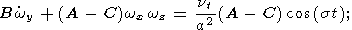 | (10b) |
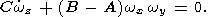 | (10c) |
Using relations (6) and (7), it is easy to see that the ratio of terms
Cwz and ( B-A)wxwy
in (10c) is
of the order of
hevt /(ga), where
e is the flattening of the planet and
g is the gravity on its surface. This ratio is negligibly small for all planets
of the
solar system, and the approximation
wz = w
= const is valid with
a very high accuracy. In this approximation, the solution of equations
(10a) and (10b) describing forced nutation and precession is
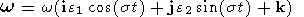 | (11a) |
where
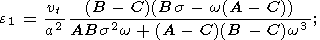 | (11b) |
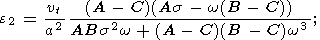 | (11c) |
Substituting relations (11) in the well-known Euler relations between Euler
angles ( 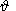 E, fE,
yE ) and ( wx, wy,
wz ) [Landau and Lifshitz,
1964]
E, fE,
yE ) and ( wx, wy,
wz ) [Landau and Lifshitz,
1964]
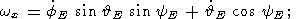 | (12a) |
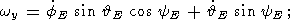 | (12b) |
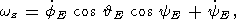 | (12c) |
we obtain a system of three nonlinear ordinary differential equations with
respect
to three unknown functions
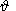 E, fE,
yE.
In the case of an axially symmetrical body ( A=B and
e1 = e2
= e, where
e is defined by (7))
these equations have an elementary (Poinsot) solution in the form
E, fE,
yE.
In the case of an axially symmetrical body ( A=B and
e1 = e2
= e, where
e is defined by (7))
these equations have an elementary (Poinsot) solution in the form
 | (13a) |
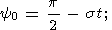 | (13b) |
and
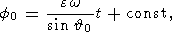 | (13c) |
which show, that the angular frequency and amplitude of nutational
motion in space are
and
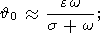 | (13d) |
(if this amplitude satisfies the condition
|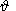 0|
0| 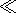 1 )
1 )
4. First-order Approximation for a Slightly Triaxial
Body
To estimate the effects of triaxiality of the planet in the first approximation,
we first perform some simple transformations. Multiplying (12a) and (12b) by
cosyE and
sinyE and then subtracting
the
results, we express
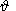 E in terms of
e1, e2
as follows:
E in terms of
e1, e2
as follows:
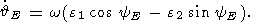 | (14a) |
Analogously, multiplying (12a) and (12b) by
sinyE and
cosyE and then summing the results,
we have
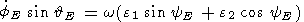 | (14b) |
To linearize these equations, their solutions are represented by the superposition
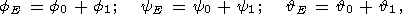 | (15) |
where
f0, y0,
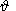 0 are the solutions of axially
symmetrical problem (13a)-(13c), and
f1, y1,
0 are the solutions of axially
symmetrical problem (13a)-(13c), and
f1, y1,
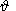 1 are
small corrections due to the triaxiality effects of the inertia ellipsoid.
1 are
small corrections due to the triaxiality effects of the inertia ellipsoid.
Substituting (15) and (11a) into (14a), (14b), and (12c) and neglecting the terms
of the order
of
h2, we obtain
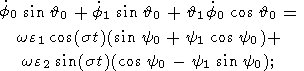 | (16a) |
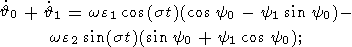 | (16b) |
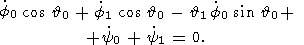 | (16c) |
Transforming, in accordance with (13b), the main terms in the right-hand sides of
these equations,
and taking into account, that the zero-order values of
f0, 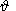 0,
y0 are connected with
e, w and
s by relations (13), we obtain, after differentiation
of these relations
with respect to the time,
0,
y0 are connected with
e, w and
s by relations (13), we obtain, after differentiation
of these relations
with respect to the time,
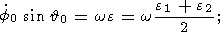 | (17a) |
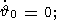 | (17b) |
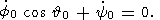 | (17c) |
Using these relations, equations (16) can be rewritten as follows:
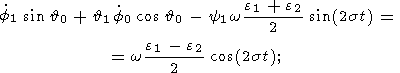 | (18a) |
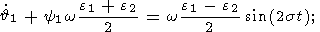 | (18b) |
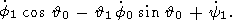 | (18c) |
Eliminating
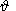 0 and
f0 from these relations with the
help of (13a) and (17c), we finally obtain the
system of three inhomogeneous linear ordinary differential equations
0 and
f0 from these relations with the
help of (13a) and (17c), we finally obtain the
system of three inhomogeneous linear ordinary differential equations
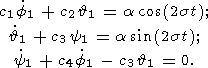 | (19) |
with the coefficients
and
Since the system of equations (19) is of the third order, it has three linearly independent
homogeneous
solutions. It is easy to show, however, that these solutions are not interesting
for the problem under
consideration, because they describe the small variations in Euler angles caused
by an arbitrary
infinitesimal rotation of the fixed reference frame.
The inhomogeneous solution of (19) has the form
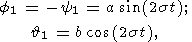 | (20) |
where
and
These expressions fully determine first-order short-period perturbations of the nutational
and
precessional motion caused by the triaxiality of the planetís figure.
To find short-period motion perturbations of the vector
w,
we introduce a fixed Cartesian reference frame ( e1, e2, e3 )
in such a way that the axis
e3 coincides with the axis of the unperturbed
cone of herpolhode, and
fE is equal to the angle between
the nodal
line and vector
e1. Then the
relations between components ( w1, w2,
w3 ) and Euler
angles ( 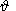 E, fE,
yE ) are completely analogous
to (12a)-(12c) after replacement of
fE by
yE and
yE by
fE :
E, fE,
yE ) are completely analogous
to (12a)-(12c) after replacement of
fE by
yE and
yE by
fE :
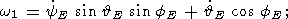 | (21a) |
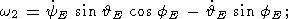 | (21b) |
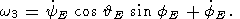 | (21c) |
In the case of nutational motion of any actual planet, its spatial amplitude
ew / (s
+ w) does not
exceed a few seconds of arc, and we can use, instead of (13a), a more simple expression
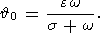 | (22) |
Substituting (15), (13b), (13c), (22), and (17) into (21), we have
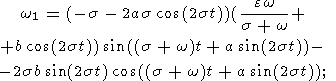 | (23a) |
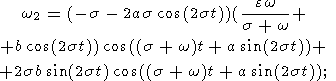 | (23b) |
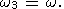 | (23c) |
Like the first-order corrections to Euler angles (20), these expressions contain
only short-period
(semidiurnal) perturbations.
5. Long-period terms in the second-order approximation
Now, we will use the well-known Poinsot's theorem stating that the rolling of polhode
over
herpolhode takes place without sliding. On the strength of this theorem, a general
method for
the calculation of long-period herpolhode perturbations may be formulated as follows.
Let the
total length of the vector
w trajectory in the moving reference frame
( x, y, z )
is defined by the expression
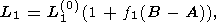 | (24a) |
where
L1(0) is the length of the vector in the case of an
axially symmetrical planet ( A=B ) and
f1(B-A) is a small correction due to +effects of
triaxiality. Because this trajectory coincides with circle (6) if
A=B and with ellipse (11a) if
A 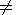 B, the function
f1 actually describes the known
difference between the length of ellipse (11a) with the semiaxes
we1,
we2
and the length
2pwe
of
circle (6).
B, the function
f1 actually describes the known
difference between the length of ellipse (11a) with the semiaxes
we1,
we2
and the length
2pwe
of
circle (6).
Likewise, using relations (23), the total length of the
w trajectory in
the fixed reference frame ( e1, e2, e3 ) can be
represented
in the form
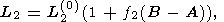 | (24b) |
where
L2(0) = |s / (s + w)| L1(0)
is the
total length of the herpolhode in the biaxial case and
f2(B-A) describes the difference between the lengths
in the triaxial and biaxial cases.
As mentioned before, the absence of exact expressions for the Euler angles in terms
of known components
wx(t), wy(t)
precludes direct determination
of this function. However, expressions (23)
readily provide the part of this function
f2(s)(B-A) which is connected
with short-period (semidiurnal) perturbations of herpolhode. Using this value,
the total perturbation of herpolhode length can be represented as a sum of the
known short-period perturbation
L2(0)f2(s)(B-A)
and
unknown long-period perturbation
L2(0)f2(1)(B-A)
that describes
variation in the "mean'' herpolhode radius:
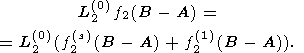 | (25a) |
In accordance with Poinsot's theorem, the condition of the polhode rolling over herpolhode
without
sliding is that the trajectories described by the angular velocity vector during
equal time intervals have
the same lengths in moving and fixed reference frames:
where
T1 and
T2 are full revolution periods of
the vector
w in the moving and fixed reference
frames, respectively. Since these values are connected through the relation
the unknown value
f2(1)(B-A) can be expressed in terms
of the known
functions
f1(B-A) and
f2(s)(B-A) in the following, very
simple form:
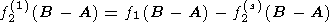 | (25b) |
Then, variation in the mean radius of herpolhode (which coincides with variation
in the
nutation amplitude
dA multiplied by
w ) may be represented in the form
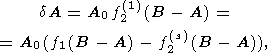 | (26) |
where
A0 is the unperturbed nutation amplitude corresponding
to the axially symmetrical approximation.
In accordance with (11), the complete trajectory length of the vector
w in the moving reference frame
( x, y, z ) is
Developing the integrand function as the Taylorís series in small parameter
k = (e12
- e22)/(e12
+ e22)
with the help of (11b) and (11c) and neglecting terms of the order of
k4, we have
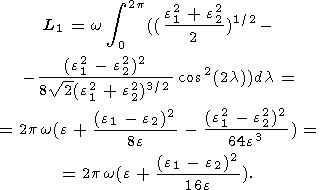 | (27a) |
Comparing this expression and relation (24a) yields
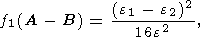 | (27b) |
where the nutation amplitudes
e1, e2
and
e are defined by expressions (11b), (11c), and
(7), respectively.
Strictly speaking, the definition of the complete trajectory length of the vector
w in the fixed reference frame ( e1, e2, e3 needs some refinement,
because this trajectory is generally nonclosed.
In fact, it is obvious that, since the period of short-period perturbations is equal
to
p/s and the
period of nutational motion is equal to
2p/|s + w|, this trajectory is closed only if
s = k(s
+ w), where
k is any integer number. Of course,
nutation frequencies of actual planets do not satisfy this condition, and
the herpolhode is not a closed curve.
In order to apply Poinsot's theorem to the case of nonclosed trajectory of the
angular velocity vector in space, we define the "mean length'' of this trajectory
as follows:
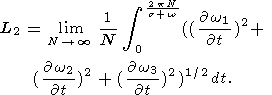 | (28) |
Substituting (23) into (28) and expanding, as before, the integrand function in Taylor's
series with
the accuracy of the order of
k4, we obtain
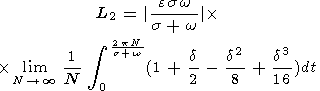 | (29a) |
where
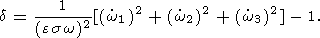 | (29b) |
Substituting (20a-c) into (26a, b), we have
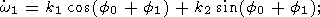 | (30a) |
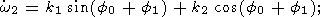 | (30b) |
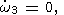 | (30c) |
where
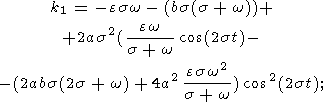 | (31a) |
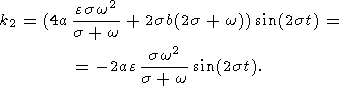 | (31b) |
Substituting these expressions into (29), (30a), and (30b) and neglecting the terms
of the
fourth and higher orders, we have
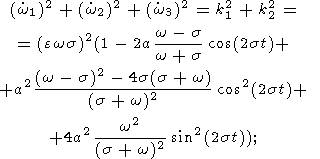 | (32a) |
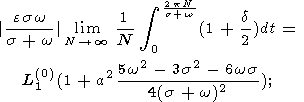 | (32b) |
)
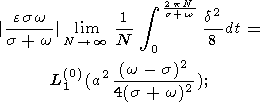 | (32c) |
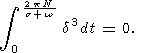 | (33) |
Summing these expressions, we finally obtain
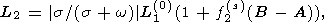 | (34a) |
where
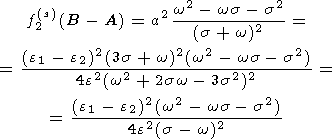 | (34b) |
Substituting (34b) and (26b) into (23), we obtain the final value of the correction
to the mean
nutation amplitudes
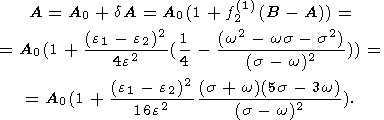 | (35) |
Note that this correction vanishes if
s = -w or
s = 3w/5.
The first root corresponds to the precession frequency. Vanishing of this expression
for the precession frequency implies that the precessional constant depends
only on the value
Ď - (A+B)/2 but not on the difference of equatorial moments of inertia
B-A.
The second root, as well as the denominator root
s = -w, corresponds
to the case of high nutation frequencies in space as compared with the period of
diurnal
rotation (these frequencies correspond to the spatial periods of nutational motion
Ts = 5T0/8 and
Ts = T0/2,
respectively, where
T0 = 2p/w
is one sidereal day).
Nutational motion with the period
Ts = T0/2 takes place only
in the case of synchronised diurnal and orbital rotation (if at the points of equinoxes
the orientation of the planet's principal equatorial moments of inertia is invariable
in space).
In this case, the nutation amplitudes are obviously determined not by the mean values
of
A,
B averaged over the total period, but by their "effective'' values in the
vicinity of points at which the tidal torque is maximum. In this specific case,
the corrections to the mean nutation amplitudes are proportional to
(e1 e2)/e rather than
(e1 e2)2/e2. This qualitative consideration
explains, why second-order correction (35) tends to infinity in the limiting case
s w.
w.
Acknowledgment
This work was supported by the Russian Foundation for Basic Research, project No.
98-05-64419.
References
Landau, L. D. and E. M. Lifshitz, Mechanics, Moscow, Nauka, 1964 (in Russian).
Molodensky, S. M., Tides, Nutation, and Internal Structure of the Earth,
Moscow,
Nauka, 1980, 214 pp. (in Russian).
Zharkov V. N., S. M. Molodensky, E. Groten, A. Brzezinski, and P. Varga.
The Earth and its rotation. Low-frequency geodynamics,
Heidelberg, Wichman Verlag, 1996, 531 pp.
Load files for print and local use.
This document was generated by TeXWeb
(Win32, v.1.0) on February 26, 1999.
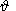 E, fE,
yE, which describe the position
of the body-fixed (Tesserand's) axes ( x, y, z ) with
respect to an immobile reference frame. At the same time, dynamic equations of motion
of an actual
planet model define only the components
(wx,
wy,
wz) of the angular velocity
vector
w with respect
to a moving reference frame. In the case of an axially symmetrical planet (equatorial
moments of
inertia satisfy the condition
A = B ) the Euler angles are connected with these components through
well-known Poinsot's formulae (see, for example, [Landau and Lifshitz, 1964]), but in the case
A
E, fE,
yE, which describe the position
of the body-fixed (Tesserand's) axes ( x, y, z ) with
respect to an immobile reference frame. At the same time, dynamic equations of motion
of an actual
planet model define only the components
(wx,
wy,
wz) of the angular velocity
vector
w with respect
to a moving reference frame. In the case of an axially symmetrical planet (equatorial
moments of
inertia satisfy the condition
A = B ) the Euler angles are connected with these components through
well-known Poinsot's formulae (see, for example, [Landau and Lifshitz, 1964]), but in the case
A  B Euler's relations between
B Euler's relations between
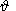 E, fE,
yE and
(wx, wy,
wz) present a rather complicated
(nonlinear)
system of ordinary differential equations which has not been investigated in all
details as yet.
E, fE,
yE and
(wx, wy,
wz) present a rather complicated
(nonlinear)
system of ordinary differential equations which has not been investigated in all
details as yet.
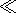 1| ) Euler's
equations can be solved by using the
perturbation method in
powers of this parameter; in such an approach, first-order (in
h ) corrections describe
only short-period (semidiurnal) perturbations of the values
1| ) Euler's
equations can be solved by using the
perturbation method in
powers of this parameter; in such an approach, first-order (in
h ) corrections describe
only short-period (semidiurnal) perturbations of the values
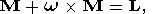
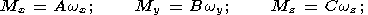
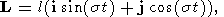
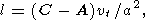
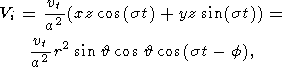
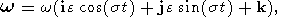
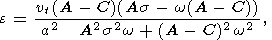
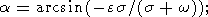
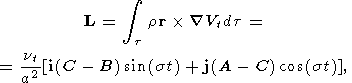
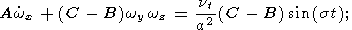
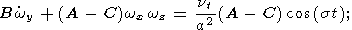
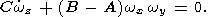
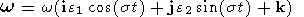
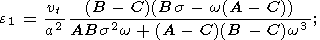
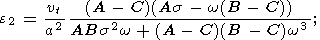
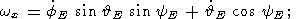
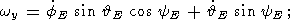
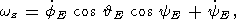

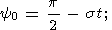
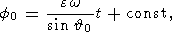
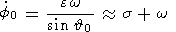
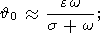
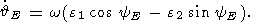
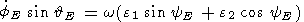
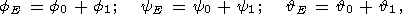
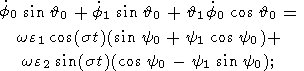
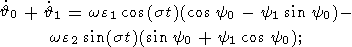
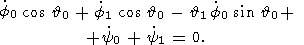
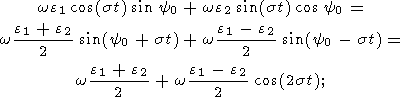
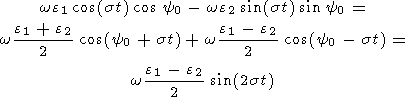
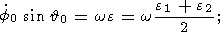
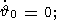
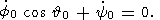
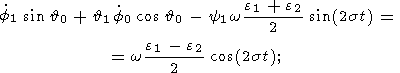
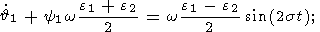
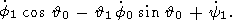
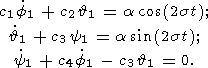
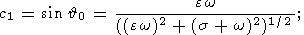
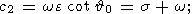
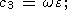
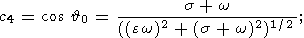
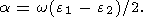
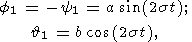
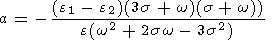
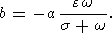
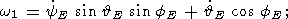
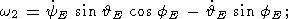
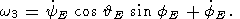
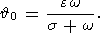
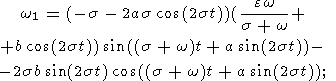
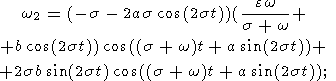
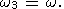
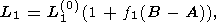
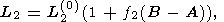
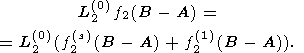
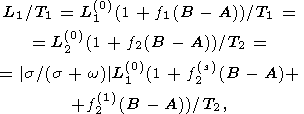
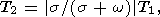
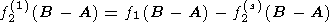
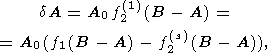
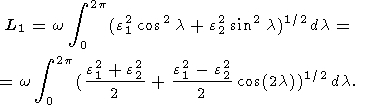
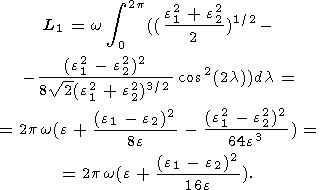
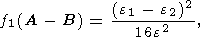
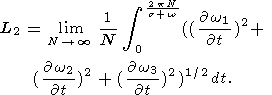
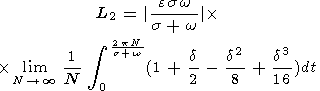
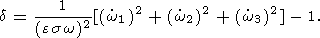
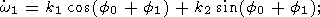
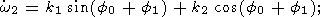
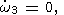
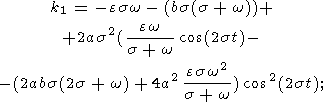
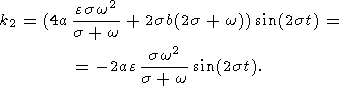
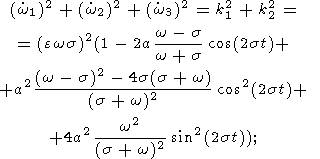
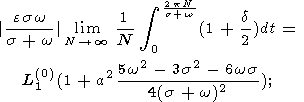
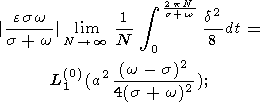
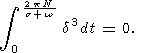
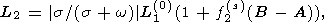
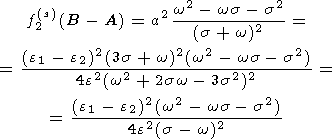
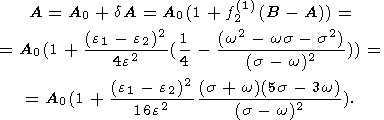
 w.
w.
