11. Thermodynamic Grüneisen Parameter

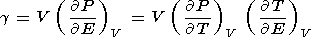
The thermodynamic Grüneisen parameter is defined by (8) or (14), which further lead to several useful identities

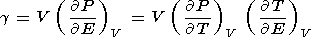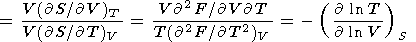(105)

The typical values of g by (8) or (14) range from 1 to 2 (see, e.g., Table 2 and Pankov et al. [1997]). Of 54 minerals treated by D. Anderson [1989], only five have g greater than 2, and none has g over 3. Low values of g are seldom encountered: e.g., g = 0.4 for a -quartz, 0.3 for coesite, and even g< 0 for U ₂ O, AgJ, and b -quartz.

11.1. P- V- T derivatives of g

The logarithmic derivatives of g with respect to V (or P ) are characterized by the parameter q, for which from (8) and (100), we find

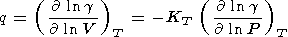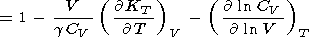(106)

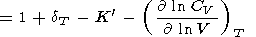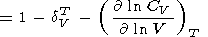(107)

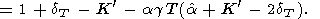(108)

As noted earlier (see (57) or (69) and (8)), in general, the C_V = constant case leads to g = g(V), and therefore, q = q(V) or q = constant. If C_V is only temperature-dependent, there are three possibilities: (1)  q = q(V), (2)  q = constant 1 (i.e., d_V^T = constant 0 ), and (3)  q = 1 ( d_V^T = 0, K = d_T(V), and t = aK_T = constant). Thus, both C_V = constant and C_V = C_V(T) conditions result in the case that the two inequalities are equivalent:

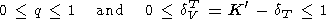(109)

If we simply assume that g is only volume-dependent, then from (14), (33), and (106),

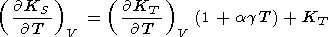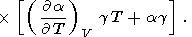(110)

Placing in (110) for (K_S/ T)_V by identity (99),

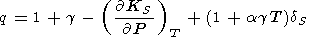(111)

However, in the general case, g = g(V, T), and from the formula for g in (18), we find

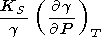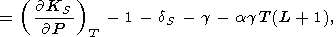(112)

which, upon excluding L by (85), yields the important identity [Bassett et al., 1968]

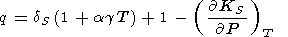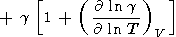(113)

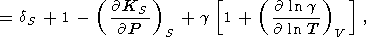For g = g(V), this identity is reduced to (111).

In section 6, we have already referred to some data on values of q. In general, values of q can be inferred from the following sources: 1) thermodynamic estimation by (108) or (111), 2) fit of the Mie-Grüneisen type EOS to data on a(T), C_P(T), and K_S(T) at P = 0, 3) shock wave data [e.g., McQueen, 1991; Duffy and Ahrens, 1992a], 4) adiabatic temperature gradient measurements [Boehler, 1982, 1983], 5) spectroscopy of solids [e.g., Reynard et al., 1992; Williams et al., 1987], 6) theoretical EOS models [e.g., Isaak et al., 1990], 7) analysis of geophysical data [O. Anderson, 1979b; D. Anderson, 1989]. The values of q estimated by (108) and given in Table 3 and Pankov et al. [1997], fall into the interval 0.5-2, except for the high values for coesite (about 17), fayalite (2-3), and Fe-perovskite (4-5). Small negative values were also found for enstatite and FeO (probably, due to inaccurate input data). With increasing T at P = constant or with increasing P at T (or S = constant), q decreases (see also section 6).

For the temperature derivative of g, we again have the expansion of type (29)

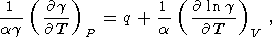(114)

where the intrinsic anharmonicity term can be evaluated using (18) and (85)

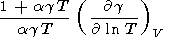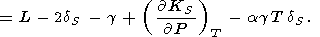(115)

This term is usually negative and completely prevails in (114) at T < Q, but at high temperatures, its value is comparable to q. Thus, the frequently used assumption that g = g(V) is unsatisfactory in the general case, and the temperature effect on the Grüneisen parameter can serve as a measure of the validity of the Mie-Grüneisen EOS [Molodets, 1998].

Another suitable representation of (g/ T)_V follows from (8) and (69) [Stacey, 1977b]

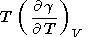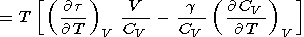(116)

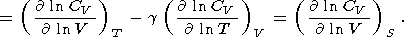If g = g(V), then either C_V = C_V(S) or C_V = constant. The case C_V(S) results in

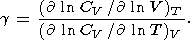(117)

Moreover, (117) leads to C_V(V, T) = C_V(Q/T) and Q/T = f(S), so that g is represented as g = -d lnQ/d ln V, where Q is a characteristic temperature.

11.2. Some explicit volume dependences of g

The frequently used volume dependences of the latice Grüneisen parameter were given in section 6. The Rice [1965] formula is also of interest

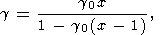(118)

which is derived from (110) under the condition that

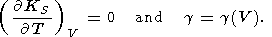The inequality ( K_S/ T)_V > 0 (see section 10 and D. Anderson [1989]) holds true of many materials and therefore gives a lower limit for their dependence g(V), i.e., q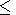 1 + g and g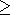 g(x) by (118). This limit was previously found from the Mie-Grüneisen EOS [Kalinin and Panov, 1972], but it also follows from the given thermodynamic consideration.

Equation (118) can be considered a partial case of the more general representation g = g(V, S). We introduce a parameter l defined as

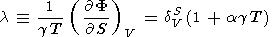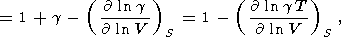(119)

where F = K_S/r. Assuming that l = l(S) or l = constant and using (119) and (105), we find by integration that

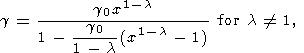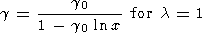(120)

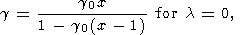where g₀ = g₀(S) and V₀ = V₀(S). These dependences of g(x) for various l are illustrated in Figure 10. One can see that they are quite sensitive to variations of l in the interval from 0 to 1.

12. Adiabatic Temperature Gradient

In geophysics, the conditions close to adiabatic are realized in the convecting mantle and core, as well as in seismic wave propagation. Furthermore, the state at the initial part of Hugoniot are close to adiabatic. Adiabats of a given material form a one-parametric family of curves. In this case, the temperature and pressure are related by the adiabatic gradient t_S, which, considering its definition by (10) and relations in section 2, can be written in the form

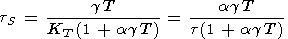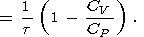(121)

Typical values of t_S found by (121) are given in Table 2 and Pankov et al. [1997].

Direct measurements of t_S at high pressures and temperatures were made in a series of works [Dzhavadov, 1986; Boehler and Ranakrishnan, 1980; Boehler, 1982, 1983]. Chopelas and Boehler [1992] reported corrections to the Boehler [1982] initial results on t_S.

12.1. P-V-T derivatives of t_S

We consider the basic identities and approximaions for the derivatives. Denoting by n the logarithmic volume derivative of t_S and using q by (106), we have

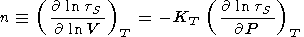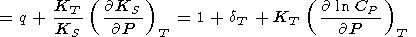(122)

(compare with (45)).

Formula (122) can be represented in various forms, using q by (113), (115), and (58). It is clear that n decreases by isothermal or adiabatic compression. The simplest estimate of n is given by assuming that

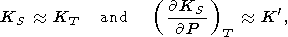hence,

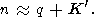(123)

The typical values of q = 1-2 and K = 4-5 yield n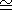 5-7. If we neglect the last term in (122) at T > Q, then n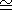 1 + d_T [Chopelas and Boehler, 1992].

Changing from variables (V, S) to (V, T), the adiabatic derivative with respect to volume takes the form

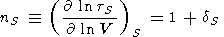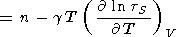(124)

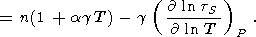Approximation (89) and n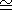 1 + d_T give n_S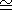 n - g. Writing the derivative of t_S with respect to T in the form of (29),

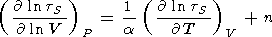(125)

or after substituting ( lnt_S/ T)_V by (124),

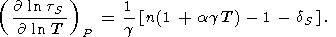(126)

The values of (( lnt_S)( ln V))_P and n (an extrinsic anharmonic contribution) calculated by (126) and (122) are given in Table 2 and Pankov et al. [1997]. They show that the intrinsic anharmonic term dominates in (125).

Note that the t_S parameter occurs in any expression when changing variables P, S to P, T : for example,

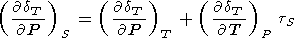(127)

which was used in deriving (98).

12.2. Explicit volume dependences of t_S

For a moderate compression, the volume dependence of t_S can be described by the power law

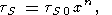(128)

where n = n (T) or constant, t_S0 = t_S0 (T) and V₀ = V₀ (T). This formula was used to fit the measured t_S values to P = 50 kbar and T = 1000 K [Boehler and Ramacrishnan, 1980; Boehler, 1982].

However, Chopelas and Boehler [1992], accounting for the variation of d_T with V (see (46) and (47)), found that the linear dependence of lnt_S on V (n = mx) better describes teir data on t_S than the power law, and consequently,

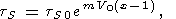(129)

where constant m is determined by the approximation

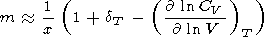(130)

(see (122), where C_P is approximately C_V ). Thus, on the condition that ( ln C_V/ ln V)_T is independent of V, the derivative (d_T/ x)_T can be found given knowledge of the m value. Isaak [1993] applied this method to evaluate the derivative ²K_S/ P T with the help of (91).

12.3. EOS based on data for t_S (P, T).

Measured values of t_S(P, T) allow us first to find the isobaric specific heat [Dzhavadov, 1986]

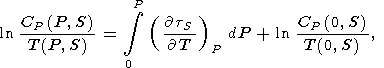(131)

which is deduced from the identity ² T/ P S = ² T/ S P. The integral in (131) is taken over an adiabat, and the specific heat versus temperature, C_P(T), for P = 0, is assumed to be known. Then, given a reference isotherm V(P, T₀ ), from (14), we can find the thermal EOS in the form

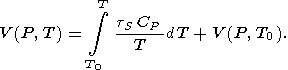(132)

Conversely, given the thermal EOS and t_S(T) at P = 0, (14) gives C_P(T) at P = 0, and thus, the caloric EOS can be determined.

This document was generated by TeXWeb (Win32, v.1.0) on February 10, 1999.