
Here, we consider the two useful Anderson-Grüneisen parameters in more detail [Grüneisen, 1926; O. Anderson, 1966a, 1967]: the isothermal dT parameter introduced above (see (31)) and the adiabatic dS parameter defined as
 | (82) |
Both parameters are used in geophysical and physical studies [Chung, 1973; Barron, 1979]. The parameter dT is largely applied in analyzing the P-T behavior of a, KT, and t, and dS is used to estimate the temperature dependence of KS and to treat the relations between elastic properties (elastic wave velocities) and thermodynamic data [D. Anderson, 1987; O. Anderson et al., 1987; Isaak et al., 1992; Duffy and Ahrens, 1992a, 1992b; Agnon and Bukowinski, 1990b].
As the temperature decreases in the range T 300 K at P = constant, both parameters dS and dT sharply increase due to decreasing a, but at high temperatures, T > Q, they become more or less constant [O. Anderson et al., 1992a]. From (16), we derive the identity relating dT and dS [Birch, 1952]
 |
 | (83) |
which was used to calculate the dT values listed in Table 3 and Pankov et al. [1997]. Deriving (83), we find in passing that
 |
 |
 | (84) |
 |
where, for convenience, the notation
 | (85) |
is introduced.
The values of
L and
( g/
g/ T)P at
P = 0,
calculated by (84) and (85),
are also presented in Table 3 and Pankov et al. [1997].
T)P at
P = 0,
calculated by (84) and (85),
are also presented in Table 3 and Pankov et al. [1997].
Data for some minerals [O. Anderson et al., 1992a]
show that
( g/
g/ T)P=0
T)P=0 0 over a wide temperature range. Assuming that
(
0 over a wide temperature range. Assuming that
( g/
g/ T)P = 0 for
CV = constant
(T > Q), (84) gives
T)P = 0 for
CV = constant
(T > Q), (84) gives
 | (86) |
Moreover, since CV = constant, this case results in q = 0, and consequently, according to (35) and (42),
 | (87) |
However, the estimation of
dT by (42) for
q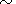 1 is more
accurate than the values from (87). Then, one might expect that
in (84)
1 is more
accurate than the values from (87). Then, one might expect that
in (84)
 |
for CV constant.
Using (83), identity (84) can be rearranged to the form
 |
 | (88) |
If the last term in (88) is small, then [O. Anderson et al., 1992a]
 | (89) |
This approximation is recommended for evaluating of the Anderson-Grüneisen parameters at high temperatures, when there are no sufficient data for applying (83) or (88).
In addition to the analysis of the parameter
dT(P, T) described
in sections 6 and 8, we consider the following
features in the behavior of
dT. 1) If
g = g(V),
then
q = q(V), but generally speaking,
dT = dT(V,
T) since
CV = CV(V, T) and
K = K
= K (V, T). 2) If
CV = CV(T),
then (42) holds true, and moreover,
g = f(V)/CV(T),
q = q(V),
although, generally speaking,
K
(V, T). 2) If
CV = CV(T),
then (42) holds true, and moreover,
g = f(V)/CV(T),
q = q(V),
although, generally speaking,
K = K
= K (V, T) and
dT = dT(V,
T). Combining the former of these assumptions
with the condition
KT = KT(V) (i.e.,
dT = K
(V, T) and
dT = dT(V,
T). Combining the former of these assumptions
with the condition
KT = KT(V) (i.e.,
dT = K ), we
find
), we
find
 | (90) |
and CV therefore takes the form
 |
In section 6.2.2, the arguments were given for decreasing
dT with pressure. The same behavior
of this parameter
follows from the approximation (42) since both
K and
q decrease with pressure. The exact relations for the
P and
T derivatives of
dT result from the definition
of
dT by (31)
and
q decrease with pressure. The exact relations for the
P and
T derivatives of
dT result from the definition
of
dT by (31)
 | (91) |
 | (92) |
If the first term in (91) prevails, we have an unusual case
(( dT)/(
dT)/( P))T > 0.
Neglecting the second temperature derivative in (92) (at
least at room temperature), we find that
(
P))T > 0.
Neglecting the second temperature derivative in (92) (at
least at room temperature), we find that
( dT/
dT/ T)P < 0.
However, the approximation
dT = K
T)P < 0.
However, the approximation
dT = K (more realistic at
T > Q )
gives, by constast,
(
(more realistic at
T > Q )
gives, by constast,
( dT/
dT/ T)P > 0 because of
(
T)P > 0 because of
( K
K /
/ T)P > 0. Experimental
data
indicate that
((
T)P > 0. Experimental
data
indicate that
(( 2 KT)/(
2 KT)/( T2))P for
T > Q is negative and small in value
[O. Anderson et al., 1992a].
T2))P for
T > Q is negative and small in value
[O. Anderson et al., 1992a].
Finally, the EOS of type (28), which we used to calculate the
thermal expansion coefficient by (36), allows us to determine
the explicit pressure (or volume) dependence of
KT along an
isotherm. Retaining in (36) only the terms involving
dK 0/dT,
we obtain
0/dT,
we obtain
 |
 | (93) |
where
f denote the derivative of
f with respect to
x. This
approximation generalizes the similar Birch formula that follows
from (93) for
dK
denote the derivative of
f with respect to
x. This
approximation generalizes the similar Birch formula that follows
from (93) for
dK 0/dT =
0 [Birch, 1968].
However, when using usual EOS
types,
dT from the Birch formula increases
with
P (except for the Murnaghan EOS for which the behavior of
dT depends on the sign of the
difference
K
0/dT =
0 [Birch, 1968].
However, when using usual EOS
types,
dT from the Birch formula increases
with
P (except for the Murnaghan EOS for which the behavior of
dT depends on the sign of the
difference
K - dT0 ).
Again, we convince ourselves that the term with
derivative
dK
- dT0 ).
Again, we convince ourselves that the term with
derivative
dK 0/dT is
important in analyzing
the thermal expansion by (28).
0/dT is
important in analyzing
the thermal expansion by (28).
 Figure 8 shows several curves of
dT(x) calculated using
(93) and EOS (37), which correspond to the curves of
a in
Figures 1 and
3 (the straight line
dT = 6x - 1 by (47) is
also drawn for comparison). The favored value of
dK
Figure 8 shows several curves of
dT(x) calculated using
(93) and EOS (37), which correspond to the curves of
a in
Figures 1 and
3 (the straight line
dT = 6x - 1 by (47) is
also drawn for comparison). The favored value of
dK 0/dT is
2
0/dT is
2 10-3 K
-1 (see section 6.2), and deviations from it
substantially affect the
dT values at compressions in
the lower mantle. At high temperatures, according to (42), we
have also the lower limit for
dT,
dT > K
10-3 K
-1 (see section 6.2), and deviations from it
substantially affect the
dT values at compressions in
the lower mantle. At high temperatures, according to (42), we
have also the lower limit for
dT,
dT > K - 1 [O. Anderson et al., 1992a].
- 1 [O. Anderson et al., 1992a].
Elastic moduli and their
P-V-T derivatives are the
characteristics constituting the basis of the Earth's interior
thermodynamics [Birch, 1952, 1961;
Sumino and O. Anderson, 1984;
D. Anderson, 1967, 1987, 1989;
O. Anderson et al., 1992a;
Duffy and D. Anderson, 1989;
Bina and Helffrich, 1992;
Duffy and Ahrens, 1992a, 1992b].
These quantities also serve as
parameters of EOS's. The simplest estimates of adiabatic and
isothermal bulk moduli at high pressure are given by their
linear pressure dependences, which, however, begin to
overestimate the bulk modulus at a compression of about
x < 0.85.
The
P-T variation of the pressure derivative was
considered in many papers devoted to EOS's (see section 3). In
order to assess the applicability of empirical EOS's, one
often uses a relation between the first
K
 (
( KT/
KT/  R)T and second
K
R)T and second
K

 (
( 2KT/
2KT/
 P2)T
pressure derivatives at
P = 0 [Pankov and Ullmann, 1979a;
Jeanloz, 1989;
O. Anderson, 1986;
Hofmeister, 1991b]. Values of
K
P2)T
pressure derivatives at
P = 0 [Pankov and Ullmann, 1979a;
Jeanloz, 1989;
O. Anderson, 1986;
Hofmeister, 1991b]. Values of
K and
KK
and
KK
 at
P = 0 generally lie in the intervals 4-6 and
-(5-10), respectively. The uncertainty in
(
at
P = 0 generally lie in the intervals 4-6 and
-(5-10), respectively. The uncertainty in
( KS/
KS/ P)T (measured by ultrasonic or Brillouin
scattering methods) can reach 1-5%
(with allowance for data from various laboratories) or, in some
cases, 20% and even 50%. Anomalous values of
K
P)T (measured by ultrasonic or Brillouin
scattering methods) can reach 1-5%
(with allowance for data from various laboratories) or, in some
cases, 20% and even 50%. Anomalous values of
K and
K
and
K
 are sometimes reported (see references in tables of
Pankov et al. [1997]): for example,
K
are sometimes reported (see references in tables of
Pankov et al. [1997]): for example,
K = 5-7 (garnet),
K
= 5-7 (garnet),
K = 9-14 (pyroxene),
and
KK
= 9-14 (pyroxene),
and
KK
 = -60 (spinel), which are assumed to take
on more usual values as pressure increases.
= -60 (spinel), which are assumed to take
on more usual values as pressure increases.
Let us turn our attention to the relations between the adiabatic-isothermal derivatives of KS and KT. Changing the variables P and S to P and T, we find
 | (94) |
where
dS is defined by (82). The derivative
( KS/
KS/ P)S characterizes the curvature of an adiabatic
P-V or a Hugoniot
curve. Further, from (16)
P)S characterizes the curvature of an adiabatic
P-V or a Hugoniot
curve. Further, from (16)
 |
 | (95) |
Eliminating
( g/
g/ P)T with the help of (8) and (17) (or (122))
and using
(58), we find
P)T with the help of (8) and (17) (or (122))
and using
(58), we find
 |
 | (96) |
Substituting (94) for
( KS/
KS/ P)T and (93) for
dS, we arrive at the Birch
[1952] formula
P)T and (93) for
dS, we arrive at the Birch
[1952] formula
 |
 | (97) |
The difference between the adiabatic-isothermal derivatives of KS and KT at normal conditions are generally small (1-2% for mantle minerals). Data and estimations by (94)-(97) show that we usually have
 |
(except for FeO for which
( KS/
KS/ P)T is poorly known [Pankov et al.,
1997]);
however, D. Anderson [1989] indicated the inverse
inequality
P)T is poorly known [Pankov et al.,
1997]);
however, D. Anderson [1989] indicated the inverse
inequality
 |
For our high-temperature estimates given in Table 3 and Pankov et al. [1997], it was arbitrarily assumed that
 |
Hence, using (94)-(97), we found substantial differences (up to
10-30%) between the pressure derivatives of
KS and
KT at
high temperatures. In fact, the differences are of the same
order of magnitude as the derivative increments due to
increasing temperature. Specifically, the estimated
 2KT/
2KT/ P
P T values are
3.5
T values are
3.5 10-4 (stishovite),
2
10-4 (stishovite),
2 10-4 (ilmenite),
3
10-4 (ilmenite),
3 10-4 (Mg-perovskite), and
1.7
10-4 (Mg-perovskite), and
1.7 10-4 (MgO)
and do not exceed
1
10-4 (MgO)
and do not exceed
1 10-4 for other minerals
(although some estimates appear to be negative).
10-4 for other minerals
(although some estimates appear to be negative).
Isaak [1993] estimated
 2KT/
2KT/ P
P T using an identity of type (91) and
Boehler's data on the adiabatic temperature gradient (see also
section 12.2). He found
T using an identity of type (91) and
Boehler's data on the adiabatic temperature gradient (see also
section 12.2). He found
 2 KT/
2 KT/ P
P T = (3.9
T = (3.9 1.0)
1.0)  10-4 and
(3.3
10-4 and
(3.3 0.9)
0.9) 10-4
K
-1 for MgO and olivine, respectively.
Furthermore, he showed this derivative to decrease 30% as the
pressure increases isothermally to 100 GPa. A similar order of
magnitude was found from shock wave data to be a lower limit
for this derivative value [Duffy and Ahrens, 1992a] (see
also
sections 6 and 9).
10-4
K
-1 for MgO and olivine, respectively.
Furthermore, he showed this derivative to decrease 30% as the
pressure increases isothermally to 100 GPa. A similar order of
magnitude was found from shock wave data to be a lower limit
for this derivative value [Duffy and Ahrens, 1992a] (see
also
sections 6 and 9).
In addition to the analysis of the mixed derivatives, we give the following identity
 |
 | (98) |
which we derived from (94), using (127) and
( g/
g/ T)P from (88). Note
that a similar relation of Bukowinski and Wolf [1990]
is
different from (98) (because of either a reprint or mistake). To
give an example, we substitute in (98) the values typical of
the lower mantle:
(
T)P from (88). Note
that a similar relation of Bukowinski and Wolf [1990]
is
different from (98) (because of either a reprint or mistake). To
give an example, we substitute in (98) the values typical of
the lower mantle:
( KS/
KS/ P)S = 4,
agT =
0.1,
((
P)S = 4,
agT =
0.1,
(( lndS)/(
lndS)/( lnr))S
= -1,
and
dS = 3 for
x = 1 and
dS 2 for
x = 0.7. Then,
lnr))S
= -1,
and
dS = 3 for
x = 1 and
dS 2 for
x = 0.7. Then,
 |
which is in agreement with the preceding estimates.
When considering the temperature behavior of KS and KT, the Anderson-Grüneisen parameters dS and dT are represented in the form of (29) [D. Anderson, 1987; Duffy and D. Anderson, 1989; O. Anderson et al., 1992a], which can be rewritten as
 |
 | (99) |
 |
 |
 | (100) |
In section 9, we considered the principal regularites in the
variation of
dS and
dT with pressure and
temperature (some decrease of them with
T in the vicinity of
T = 300 K,
the trend to constant values at
T > Q, and the
decrease with pressure). Now we dwell on the contributions of
the intrinsic
dVS and
dVT and extrinsic
K anharmonic terms in (99)
and (100).
anharmonic terms in (99)
and (100).
D. Anderson [1988, 1989]
pointed out that the temperature
variation of the bulk modulus at
P = constant mostly occurs by
the variation in
a ; i.e., here, the extrinsic
anharmonicity generally prevails and enhances with temperature
(due to increasing
K ). The estimates given
in Table 3 and
Pankov et al. [1997] show that, at
T = 300 K, we have
dVT < 0 (except
very uncertain data for FeO); most of
the estimates falls into an interval between
-1 and
-2 (although it was found
dVT = -17,
-5, and
-3.9 for
coesite, stishovite, and fictive Fe-perovskite phase,
respectively). According to D. Anderson [1989],
the values of
dVT are typically
between
-4 and
-1 (his table 5,
however, contains values outside this interval: 2.2 for
orthopyroxene,
-5.3 for SrTiO
3, and
-19 for CaCO
3 ). The
parameter
dVS satisfies
the inequality
|dVS| > 2 for
11 out of 54 minerals considered by D. Anderson
(specifically,
dVS = -4.1
(GeO
2 ), 3.8 (orthopyroxene),
-3.1 (SrTiO
3 ), and
-18 (CaCO
3 ). At high temperatures,
dVT can be
either positive or negative (between
-1 and
1), and
|dVS| is generally
positive, lying in the
interval 0-1.5 [Pankov et al., 1997]. Thus, as temperature
increases,
|dVT|, on average,
decreases, but
|dVS| increases.
The contribution of
dVS/dS
to (99)
is usually less than 10-30% at 300 K and does not exceed
15-60% at high temperatures. Accordingly,
dVT contributes
no more than 30-40% in (100) at 300 K and
usually less than 10% at high temperatures. From this analysis,
it follows that the extrinsic anharmonic term, although it
generally dominates in the derivatives of
KS and
KT,
decreases its contribution in the case of
KS and increases its
contribution in the case of
KT. The decrease of
dVT with temperature
leads to the approximation
). The estimates given
in Table 3 and
Pankov et al. [1997] show that, at
T = 300 K, we have
dVT < 0 (except
very uncertain data for FeO); most of
the estimates falls into an interval between
-1 and
-2 (although it was found
dVT = -17,
-5, and
-3.9 for
coesite, stishovite, and fictive Fe-perovskite phase,
respectively). According to D. Anderson [1989],
the values of
dVT are typically
between
-4 and
-1 (his table 5,
however, contains values outside this interval: 2.2 for
orthopyroxene,
-5.3 for SrTiO
3, and
-19 for CaCO
3 ). The
parameter
dVS satisfies
the inequality
|dVS| > 2 for
11 out of 54 minerals considered by D. Anderson
(specifically,
dVS = -4.1
(GeO
2 ), 3.8 (orthopyroxene),
-3.1 (SrTiO
3 ), and
-18 (CaCO
3 ). At high temperatures,
dVT can be
either positive or negative (between
-1 and
1), and
|dVS| is generally
positive, lying in the
interval 0-1.5 [Pankov et al., 1997]. Thus, as temperature
increases,
|dVT|, on average,
decreases, but
|dVS| increases.
The contribution of
dVS/dS
to (99)
is usually less than 10-30% at 300 K and does not exceed
15-60% at high temperatures. Accordingly,
dVT contributes
no more than 30-40% in (100) at 300 K and
usually less than 10% at high temperatures. From this analysis,
it follows that the extrinsic anharmonic term, although it
generally dominates in the derivatives of
KS and
KT,
decreases its contribution in the case of
KS and increases its
contribution in the case of
KT. The decrease of
dVT with temperature
leads to the approximation
 | (101) |
and additionally, in view of (89) and (99),
 | (102) |
Thus, at high temperatures, namely the isothermal, rather than adiabatic bulk modulus becomes depending mostly on volume (i.e., temperature-independent function).
In his analysis of the thermodynamic properties of the lower mantle, D. Anderson [1987, 1988, 1989] relies on seismic tomography and geoid data and assumes that the observed horizontal velocity anomalies are caused by temperature variations. Stacey [1992] showed, however, that it is not possible to explain the anomalies with a purely temperature effect, since in such a case, the geoid highs would be too great. Other hypotheses proposed to interpret the seismic anomalies were related to inhomogeneities of composiion, or partial melting, or even the presence of small amounts of fluids [Price et al., 1989; Duffy and Ahrens, 1992b; and others]. Nevertheless, following D. Anderson, below, we estimate the thermodynamic parameters for the lower mantle, considering the temperature effect formally as a limiting case.
Based on the PREM model, the formula for the acoustic
Grüneisen parameter, and tomography data,
we have in the lower
mantle
( KS/
KS/ P)S = 3-3.8,
g = 1.2
P)S = 3-3.8,
g = 1.2 0.1, and
dS = 1-1.8.
Consequently, using (89), (94), (96), (99), and (100),
we find
dT
0.1, and
dS = 1-1.8.
Consequently, using (89), (94), (96), (99), and (100),
we find
dT dS + g
= 2.2-3.0,
K
dS + g
= 2.2-3.0,
K = 3-3.8 (a small correction
can be introduced with the help of
a = a0xdT for
a0 = 4
= 3-3.8 (a small correction
can be introduced with the help of
a = a0xdT for
a0 = 4 10-5 K
-1 and
T
10-5 K
-1 and
T 2000-3000 K),
dVS
2000-3000 K),
dVS K
K - dS
= 1.2-2.8, and
dVT = dVS- g
= -0.1-1.7.
If a greater uncertainty is assumed for
g, say
- dS
= 1.2-2.8, and
dVT = dVS- g
= -0.1-1.7.
If a greater uncertainty is assumed for
g, say
 0.4, then
dT
0.4, then
dT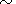 1.9-3.3 and
dSV
1.9-3.3 and
dSV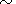 -0.4-2.0.
Thus, although the extrinsic anharmonic effects weaken with
pressure, they still prevail under the lower mantle conditions
( K
-0.4-2.0.
Thus, although the extrinsic anharmonic effects weaken with
pressure, they still prevail under the lower mantle conditions
( K > dSV
or
|dTV| ).
The intrinsic anharmonic term
dVS significantly
increases with pressure, but its isothermal analog
dVT can either
increase or decrease and reach zero.
D. Anderson, by reference to experimental data, points out the
case of
dVT
> dSV
or
|dTV| ).
The intrinsic anharmonic term
dVS significantly
increases with pressure, but its isothermal analog
dVT can either
increase or decrease and reach zero.
D. Anderson, by reference to experimental data, points out the
case of
dVT 0, which yields
dVS
0, which yields
dVS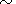 g = 1.2.
g = 1.2.
However, this value of
dSV disagrees
with data for such a
representative lower-mantle material as periclase. Using
dVT = 0 and
dT = K
 3.2-3.5 for
x = 0.7 and the Birch-Murnaghan EOS for MgO, we find
dS
3.2-3.5 for
x = 0.7 and the Birch-Murnaghan EOS for MgO, we find
dS dT- g
= 2.2-2.5 for
g = g0x
( q = 1,
see (119)). These values of
dT and
dS are, on average, still exceed
the results inferred from seismic
models. O. Anderson et al. [1992b]
noted that data for MgO can be
reconciled with seismic results by assuming that
q < 1. In
particular, our analysis leads to the following consistent
sequence of values:
dVT 0.2,
q 0.8,
g = g0xq
1.1 (for
x = 0.7 ),
dT = K
dT- g
= 2.2-2.5 for
g = g0x
( q = 1,
see (119)). These values of
dT and
dS are, on average, still exceed
the results inferred from seismic
models. O. Anderson et al. [1992b]
noted that data for MgO can be
reconciled with seismic results by assuming that
q < 1. In
particular, our analysis leads to the following consistent
sequence of values:
dVT 0.2,
q 0.8,
g = g0xq
1.1 (for
x = 0.7 ),
dT = K - dVT
3-3.3, and
dS 1.9-2.2.
In any case, the consistency to seismic data could be found in this manner if
the values derived from seismic tomography were explained by
only horizontal variations of temperature.
- dVT
3-3.3, and
dS 1.9-2.2.
In any case, the consistency to seismic data could be found in this manner if
the values derived from seismic tomography were explained by
only horizontal variations of temperature.
The consideration of the temperature behavior of
KS at
P = 0 will be added by the following two methods. One of
them uses the condition
dS = d S = constant
[O. Anderson, 1988;
Duffy and D. Anderson, 1989], and in
view of (99), yields the power law
S = constant
[O. Anderson, 1988;
Duffy and D. Anderson, 1989], and in
view of (99), yields the power law
 | (103) |
which we used to estimate the values listed in Table 2 and Pankov et al. [1997].
Another approach proposed by O. Anderson [1989]
and extended by
O. Anderson et al. [1992a] is based on data for
enthalpy. We
obtain the relation of
KS to enthalpy using a somewhat
different procedure, namely, the formula
g = aKSV/CP
from which the derivative
( KS/
KS/ H)P is found, and thus, approximately,
H)P is found, and thus, approximately,
 | (104) |
where the asterisk marks the values at a fixed temperature. By
using the parameter values from Table 2
and Pankov et al. [1997],
as well as data for enthalpy, we estimated
KS by
(104) for a number of minerals (Table 4). One can see that the
O. Anderson's method is quite efficient: the
uncertainty of the estimated values at high temperatures is
2-5%. It is also clear that both methods described above would
give more accurate results when high-temperature values for
KS ,
r
,
r ,
g
,
g ,
H
,
H , and
dS
, and
dS are used in
the respective formulas.
are used in
the respective formulas.
 In conclusion to this analysis, we show the dependence
of
KS versus
T at
P = 0 (Figure 9) calculated by the
Mie-Grüneisen EOS with
g = g0xq
for three
minerals considered in sections 6-8. Comparing the
KS curves for various values of
q = 0-2 with experimental data,
we see that it is possible to choose appropriate values of
q consistent to the data. However, considering the results
presented for the same EOS's in sections 6-8, it is not
always possible to find such values of
q for which the EOS
becomes consistent to data simultaneously for
a,
CP,
t, and
KS. Thus, as in sections 6-8, we conclude that
the thermal part of the Mie-Grüneisen EOS
does not provide
suffuciently high accuracy of all the thermodynamic parameters
calculated from this EOS.
In conclusion to this analysis, we show the dependence
of
KS versus
T at
P = 0 (Figure 9) calculated by the
Mie-Grüneisen EOS with
g = g0xq
for three
minerals considered in sections 6-8. Comparing the
KS curves for various values of
q = 0-2 with experimental data,
we see that it is possible to choose appropriate values of
q consistent to the data. However, considering the results
presented for the same EOS's in sections 6-8, it is not
always possible to find such values of
q for which the EOS
becomes consistent to data simultaneously for
a,
CP,
t, and
KS. Thus, as in sections 6-8, we conclude that
the thermal part of the Mie-Grüneisen EOS
does not provide
suffuciently high accuracy of all the thermodynamic parameters
calculated from this EOS.