Thermodynamics of deep geophysical media
V. Pankov, W. Ullmann, R. Heinrich, and D. Kracke
7. Specific Heat
The lattice specific heat of minerals at
T 1000 K is close to
the classic limit
3Rn = 3RM/m (the molar value, where
R is the gas constant and
n is the number of atoms in chemical
formula). From calorimetry, we have information on the
isobaric heat capacity
CP, which exceeds
CV by 1-3% at
300 K and 10-15% at
T > Q (Table 2 and
Pankov et al., 1997]. Since
m 20-22 g/mole
for mantle minerals, the
classic value of
CV for them is 1.13-1.25 J/g K.
Depending on mineral, the high-temperature anharmonic
corrections to
CV become singnificant either near the melting
point or even at room temperature (sometimes, at
T equal 1/6 of
the melting point) [Mulargia and Boschi, 1980;
Quareni and Mulargia, 1988;
Reynard et al., 1992;
Fiquet et al., 1992].
20-22 g/mole
for mantle minerals, the
classic value of
CV for them is 1.13-1.25 J/g K.
Depending on mineral, the high-temperature anharmonic
corrections to
CV become singnificant either near the melting
point or even at room temperature (sometimes, at
T equal 1/6 of
the melting point) [Mulargia and Boschi, 1980;
Quareni and Mulargia, 1988;
Reynard et al., 1992;
Fiquet et al., 1992].
7.1. P- V- T
derivatives of specific heat
From the identities
 2E/
2E/ V
V T =
T =  2E/
2E/  T
T V and
V and
 2S/
2S/ P
P T =
T =  2S/
2S/ T
T P, using the Maxwell
relations, we find
P, using the Maxwell
relations, we find
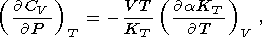 | (57) |
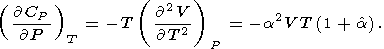 | (58) |
Note that (57) and (58) are the alternate forms of (33) and
(34), repectively. The logarithmic volume derivatives at
T = constant
can be expressed as follows:
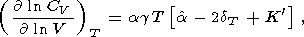 | (59) |
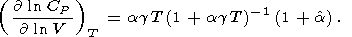 | (60) |
These identities were used to compute the derivative values
given in Tables 3 and in Pankov et al. [1997].
O. Anderson et al. [1993] noted that, for the Debye
model,
( CV/
CV/ P)T 0 and
therefore
a 2dT
- K
P)T 0 and
therefore
a 2dT
- K .
.
The difference
CP - CV satisfies the identity
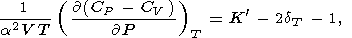 | (61) |
i.e., it decreases with pressure for usual values of
K and
dT (see Table 3 and
Pankov et al. [1997]).
and
dT (see Table 3 and
Pankov et al. [1997]).
Birch [1952] estimated the decrease in
CP with pressure in
the lower mantle, setting
a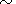 4 and
agT
4 and
agT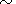 0.1.
By the power law for
CP, this gives a 13-16% decrease in
CP along an isotherm, for
x descending from 1.0 to 0.7.
According to Birch, the maximum decrease in
CP in the mantle
does not appear to exceed 20%.
0.1.
By the power law for
CP, this gives a 13-16% decrease in
CP along an isotherm, for
x descending from 1.0 to 0.7.
According to Birch, the maximum decrease in
CP in the mantle
does not appear to exceed 20%.
The adiabatic volume derivative of
CP is
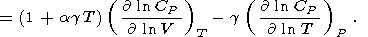 | (62) |
Substituting
( ln CP/
ln CP/ ln T)P
ln T)P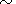 0.15 (the typical value for minerals for
T 1000 K),
g
0.15 (the typical value for minerals for
T 1000 K),
g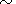 1-1.5,
agT
1-1.5,
agT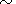 0.1, and
(
0.1, and
( ln CP/
ln CP/ ln V)T
ln V)T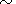 0.5 (for
a
0.5 (for
a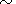 4 ),
we find
(
4 ),
we find
( ln CP/
ln CP/ ln V)S
ln V)S 0.3-0.4.
Consequently, the power law for
CP yields a 8-13% decrease of this value along the mantle
adiabat
(to
x
0.3-0.4.
Consequently, the power law for
CP yields a 8-13% decrease of this value along the mantle
adiabat
(to
x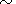 0.7 ).
0.7 ).
By using (29), the temperature derivative of
CP can be
represented in the form
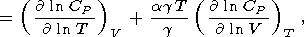 | (63) |
The second term arising from the extrinsic anharmonicity can be
estimated by making use of (58), so that (63) in conjuction with
data for
( CP/
CP/ T)P allows the first term coming from the
intrinsic anharmonicity to be evaluated. At room temperature,
(
T)P allows the first term coming from the
intrinsic anharmonicity to be evaluated. At room temperature,
( ln CP/
ln CP/  ln V)T is on the order of
(
ln V)T is on the order of
( ln CP/
ln CP/ ln T)P,
but nevertheless, the contribution of the
second term to the sum (63) is small because of the small factor
agT. At
high temperatures, this contribution
generally increases to 15-30% (perhaps, 60-70% for ilmenite
and perovskite, according to our estimates)
[Pankov et al., 1997]. In the classical limit,
CV = constant, assuming that
a
ln T)P,
but nevertheless, the contribution of the
second term to the sum (63) is small because of the small factor
agT. At
high temperatures, this contribution
generally increases to 15-30% (perhaps, 60-70% for ilmenite
and perovskite, according to our estimates)
[Pankov et al., 1997]. In the classical limit,
CV = constant, assuming that
a a(V)
and
g
a(V)
and
g g(V),
we find
(
g(V),
we find
( CP/
CP/ T)V
T)V agCV.
agCV.
Further, from (17) and (18), it is easy to obtain the identity
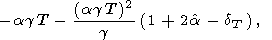 | (64) |
which we used to estimate the values of this derivative
presented in Table 3 and Pankov et al. [1997].
Then, with the
help of the identity
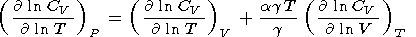 | (65) |
it is possible to compute
(( ln CV)/(
ln CV)/( ln T))V,
provided that the second term in
(65) is given by (59).
ln T))V,
provided that the second term in
(65) is given by (59).
An explicit dependence
CV(V, T) can be derived from models
and measurements of the vibrational spectra of solids (e.g.,
Pitzer and Brewer, 1961]):
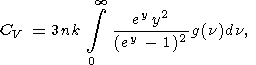 | (66) |
where
k is the Boltzman constant,
y = hn/kT,
g(n) is the
spectrum density, and
n are the lattice frequencies
including optic and acoustic modes
[Kieffer, 1979a, 1979b, 1979c,
1980;
Hofmeister, 1991a, 1991b;
Richet et al., 1992]. This method provides
information on the inadequacy of the Debye theory and the
related approximation
g = -d lnQ/d
ln V. The characteristic
temperature
Q in the Debye theory is usually estimated
from acoustic data, but
Q found from data for
CV at
T 300 K
(labelled
Qth ), on average, exceeds
the acoustic
Q (labelled
Qa ) by about 20% (larger
deviations
are common to quartz and coesite, see Table 2 and
Pankov et al. [1997] and
Watanabe [1982]).
Chopelas [1990b] found, however,
good agreement of the Debye model with the spectrum data for MgO
at pressures to 200 kbar, provided that
Q
300 K
(labelled
Qth ), on average, exceeds
the acoustic
Q (labelled
Qa ) by about 20% (larger
deviations
are common to quartz and coesite, see Table 2 and
Pankov et al. [1997] and
Watanabe [1982]).
Chopelas [1990b] found, however,
good agreement of the Debye model with the spectrum data for MgO
at pressures to 200 kbar, provided that
Q Vg,
i.e.,
q = 0.
Vg,
i.e.,
q = 0.
Spectroscopic measurements at high pressures allow us to
estimate the derivative
( CV/
CV/ P)T.
For example, the data of Chopelas [1990a, 1990b]
to 200 kbar show that
CV linearly decreases
with
P, so that the gradient
-(
P)T.
For example, the data of Chopelas [1990a, 1990b]
to 200 kbar show that
CV linearly decreases
with
P, so that the gradient
-( CV/
CV/ P)T is
17.6
P)T is
17.6 10-3 ( T = 300 K) and
0.91
10-3 ( T = 300 K) and
0.91 10-3 ( T = 1800 K) for MgO and
49.8
10-3 ( T = 1800 K) for MgO and
49.8 10-3 ( T = 300 K)
and
3.4
10-3 ( T = 300 K)
and
3.4 10-3 ( T = 1800 K) J/(mole K kbar) for forsterite.
With these values,
CV being extrapolated (by the power volume
dependence) to the maximum pressure
P = 1357 kbar in the
mantle will decrease 40-60, 8-12, and 2-3% on the 300, 1000,
and 1700 K isotherms, respectively. Comparing these results with
the decrease in
CP estimated above, we verify that the
difference
CP-CV in the lower mantle must
be exceedingly
small. From the same Chopelas' data, using also the
KT and
CV values from Table 2, we find
(
10-3 ( T = 1800 K) J/(mole K kbar) for forsterite.
With these values,
CV being extrapolated (by the power volume
dependence) to the maximum pressure
P = 1357 kbar in the
mantle will decrease 40-60, 8-12, and 2-3% on the 300, 1000,
and 1700 K isotherms, respectively. Comparing these results with
the decrease in
CP estimated above, we verify that the
difference
CP-CV in the lower mantle must
be exceedingly
small. From the same Chopelas' data, using also the
KT and
CV values from Table 2, we find
( ln CV/
ln CV/ ln V)T = 0.77 ( T = 300 K) and
0.022 ( T = 1800 K) for MgO and 0.54 ( T = 300 K) and 0.022 ( T = 1700 K)
for forsterite. These results are comparable to our
estimates of this derivative from thermodynamic data (Table 3).
ln V)T = 0.77 ( T = 300 K) and
0.022 ( T = 1800 K) for MgO and 0.54 ( T = 300 K) and 0.022 ( T = 1700 K)
for forsterite. These results are comparable to our
estimates of this derivative from thermodynamic data (Table 3).
7.2. An explicit temperature dependence of C
P at P = 0
Calorimetric data for
CP versus temperature at
P = 0 are
commonly fitted to various empirical expressions
[e.g., Fei and Saxena, 1987;
Berman, 1988;
Saxena, 1989;
Richet and Fiquet, 1991]:
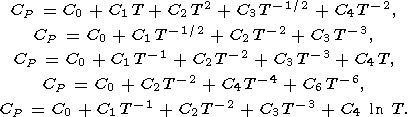 | (67) |
Richet and Fiquet [1991] showed that the last of the
above
formalas are favored but no one of them provides an accurate
description of
CP over a wide temperature range.
 In addition, Figure 6 compares
CP(T) found by the
simpler formula used by Watanabe [1982] to fit the
measurement
in the temperature interval of 350-700 K. An example of MgO
shows that the extrapolation by this formula can lead to
series errors.
In addition, Figure 6 compares
CP(T) found by the
simpler formula used by Watanabe [1982] to fit the
measurement
in the temperature interval of 350-700 K. An example of MgO
shows that the extrapolation by this formula can lead to
series errors.
As well as in the analysis of thermal expansivity in section
6.3, we calculated
CP(T) (Figure 6) from the same
Mie-Grüneisen EOS as was used to compute
a. One can see
that the theoretical curves can be reconciled with the data
shown by varying parameter
q in the limits 1-2. In so doing,
we find
q 0 for MgO,
q = 1-2 for Al
2 O
3, and
q
0 for MgO,
q = 1-2 for Al
2 O
3, and
q 0.5 for forsterite. However, these
values of
q are not always
consistent to data on
a (see section 6.3), and this fact
also suggests a certain inaccuracy of the Mie-Grüneisen
EOS
model.
0.5 for forsterite. However, these
values of
q are not always
consistent to data on
a (see section 6.3), and this fact
also suggests a certain inaccuracy of the Mie-Grüneisen
EOS
model.
8. Thermal Pressure
8.1. P- V- T
derivatives of the thermal
pressure coefficient
The thermal pressure coefficient defined by (9) or (12) is the
basic characteristic of the thermal pressure and can also be
defined as
t = ( Pth/
Pth/ T)V.
Note that
t has also the meaning of
the latent heat of expansion per 1 K. O. Anderson and his
co-workers
[O. Anderson, 1982, 1984, 1988;
O. Anderson and Sumino, 1980;
O. Anderson and Goto, 1989;
O. Anderson et al., 1982, 1991,
1992a]
paid special attention to this parameter, in
particular, in relation to their development of the rectangular
parallelepiped resonance technique for measuring elastic
properties of minerals at high temperatures.
T)V.
Note that
t has also the meaning of
the latent heat of expansion per 1 K. O. Anderson and his
co-workers
[O. Anderson, 1982, 1984, 1988;
O. Anderson and Sumino, 1980;
O. Anderson and Goto, 1989;
O. Anderson et al., 1982, 1991,
1992a]
paid special attention to this parameter, in
particular, in relation to their development of the rectangular
parallelepiped resonance technique for measuring elastic
properties of minerals at high temperatures.
The basic identities for the derivatives of
t can easily be
derived from those given in sections 6 and 7. The following
identities are especially suitable
[Brennan and Stacey, 1979;
Birch, 1978;
O. Anderson and Yamamoto, 1987]:
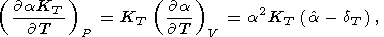 | (68) |
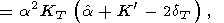 | (69) |
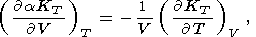 | (70) |
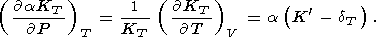 | (71) |
Formula (68) is obtained by expanding the derivative at the left
side and then by using (30); (69) is a consequence of (57), and
(70) is easily derived by equating the second derivatives of
P with respect to
V and
T taken in one order or another;
finally, (71) follows from (31) and (70).
Combining (68) and (69), we have
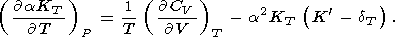 | (72) |
According to (71), for the common inequality
dT > K ,
parameter
t decreases with pressure along an isotherm.
However, at high pressure, the decrease can change to an
increase, as, e.g., in the PIB model for MgO
[O. Anderson et al., 1993].
It is clear from (68) that
t increases with
temperature at constant pressure, at least for
T < Q.
,
parameter
t decreases with pressure along an isotherm.
However, at high pressure, the decrease can change to an
increase, as, e.g., in the PIB model for MgO
[O. Anderson et al., 1993].
It is clear from (68) that
t increases with
temperature at constant pressure, at least for
T < Q.
As follows from (29), the logarithmic temperature derivative of
t at
P = constant is represented as
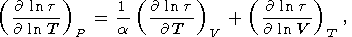 | (73) |
where the first, intrinsic anharmonic term is positive due to
(69) and can be written as the sum of two terms
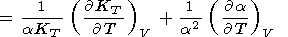 | (74) |
and the second term in (73), in view of (70) and (71), is
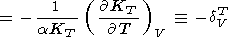 | (75) |
Here, the symbol
dVT is introduced
for convenience (see
a further analysis in section 9). Although due to large values
of
a, the intrinsic anharmonic term in (73) is dominant
in value at
T < Q, the sign of (73) at high
temperatures can be either positive or negative.
The temperature behavior of
t resembles that of
CV, so
that at
T > Q,
t tends to be independent of
temperature [O. Anderson, 1984]. Accordingly, the
thermal
pressure
Pth tends to a linear dependence on
T.
Our estimates
of
t (Table 2 and Pankov et al. [1997]) show that the
nonlinear terms in
Pth versus
T makes a contribution not
greater than 1-3% at the highest temperatures indicated in
Table 3 and Pankov et al. [1997]. The linear temperature
behavior of
Pth is considered to be the universal property of
solids at high temperatures [O. Anderson et al., 1992a].
Unlike
the temperature dependence, the extent to which
t depends
on volume at
T = constant varies from one type of solid to
another. According to O. Anderson et al. [1992a],
the earth
minerals fall into an intermediate group between
materials with significant (e.g., gold) and relatively weak
(e.g., sodium chloride, alkali metals, noble elements) volume
dependences of
t. It is important that these inferences
are based on both
P-V-T data (analysis of
Pth(V, T) )
and high-temperature data for
KT and
aKT at
P = 0 (analysis of (70)).
At first glance, the observed regularity in
t(T) at
T > Q is explained by the fact that
CV constant in this
temperature range, where, in view of (8) and (69),
g is
therefore independent of temperature. In other words, the
quasiharmonic Mie-Grüneisen EOS is seemingly
justified at high
temperatures. However, this is not quite true to be the general
case when we start with the condition
t = constant or
t = t(V)
which are compatible with the case of
CV(T) (see (69)) and therefore with a dependence
of
g on both volume and temperature [O. Anderson
and Yamamoto, 1987].
Theoretically, the departure of
CV from the Dulong and Petit
law [e,g., Mulargia and Broccio, 1983;
O. Anderson and Suzuki, 1983;
Gillet et al., 1991;
Reynard et al., 1992] is in part
related to the intrinsic anharmonicity described by the third
and higher order terms in the lattice Hamiltonian expansion. In
describing experimental data, the thermal EOS generally requires
smaller number of terms in this expansion than the caloric EOS
[Leibfried and Ludwig, 1961;
Wallace, 1972;
Davies, 1973]. Thus,
when anharmonicity in
Pth versus
T and the temperature
dependence of
g are not observed, this may suggest that
either the quasiharmonic limit for the vabrational
g has
not yet been achieved or the higher order terms in the thermal
part of the EOS are mutually cancelled
[O. Anderson et al., 1982].
constant in this
temperature range, where, in view of (8) and (69),
g is
therefore independent of temperature. In other words, the
quasiharmonic Mie-Grüneisen EOS is seemingly
justified at high
temperatures. However, this is not quite true to be the general
case when we start with the condition
t = constant or
t = t(V)
which are compatible with the case of
CV(T) (see (69)) and therefore with a dependence
of
g on both volume and temperature [O. Anderson
and Yamamoto, 1987].
Theoretically, the departure of
CV from the Dulong and Petit
law [e,g., Mulargia and Broccio, 1983;
O. Anderson and Suzuki, 1983;
Gillet et al., 1991;
Reynard et al., 1992] is in part
related to the intrinsic anharmonicity described by the third
and higher order terms in the lattice Hamiltonian expansion. In
describing experimental data, the thermal EOS generally requires
smaller number of terms in this expansion than the caloric EOS
[Leibfried and Ludwig, 1961;
Wallace, 1972;
Davies, 1973]. Thus,
when anharmonicity in
Pth versus
T and the temperature
dependence of
g are not observed, this may suggest that
either the quasiharmonic limit for the vabrational
g has
not yet been achieved or the higher order terms in the thermal
part of the EOS are mutually cancelled
[O. Anderson et al., 1982].
In conclusion to the above analysis of
t, we formulate the
following important assumptions and their consequences that can
easily be verified: (1) Let
CV be independent of
V, i.e.,
either
CV = CV(T) or
CV = constant. (2) Assume that
KT = KT(V) that is equivalent
to
dT = K . From (1), it
follows that either
t = t(V)
or
t = constant,
and in addition,
KT is either a linear function of
T or
KT(V), which leads to
q = q(V) (or
q = 1 ) and either
g = Vt(V)/CV(T)
or
g = g(V).
The
statement (2) is equivalent to either
t = t(T)
or
t = constant. If both (1) and (2) statements are
valid
(but
CV constant), then
g = const
. From (1), it
follows that either
t = t(V)
or
t = constant,
and in addition,
KT is either a linear function of
T or
KT(V), which leads to
q = q(V) (or
q = 1 ) and either
g = Vt(V)/CV(T)
or
g = g(V).
The
statement (2) is equivalent to either
t = t(T)
or
t = constant. If both (1) and (2) statements are
valid
(but
CV constant), then
g = const V/CV(T)
and
q = 1. The conditions
CV = constant and
KT = KT(V) yield
g = const
V/CV(T)
and
q = 1. The conditions
CV = constant and
KT = KT(V) yield
g = const V.
V.
8.2. Thermal pressure model
The thermal EOS resulting directly from integrating (12) is of
the form
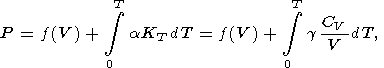 | (76) |
where
f(V) is the static lattice pressure plus the zero
oscillation pressure. The second term in (76) is the total
thermal pressure
Pth accounting for all anharmonic
contributions. This EOS can be rewritten in the form
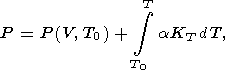 | (77) |
where, for example,
T0 = 300 K. In accordance with the
behavior of
t described above, the thermal pressure can be
approximated as [O. Anderson, 1984, 1988]
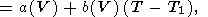 | (78) |
where
T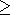 T1
T1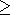 Q. As already noted, the variation with
volume in (78) is insignificant for some solids.
Q. As already noted, the variation with
volume in (78) is insignificant for some solids.
In the Mie-Grüneisen EOS, the thermal pressure
is however
defined as
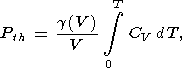 | (79) |
where the quasiharmonic approximation for
CV is used. Thus,
here, at high temperatures
T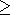 T2
T2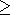 Q, when
CV
Q, when
CV constant,
constant,
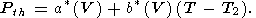 | (80) |
Even when
b(V) = b (V)
in some temperature range, the
distinction between (78) and (80) is retained since, in the general case,
g = g(V,
T) in (78) and
a
(V)
in some temperature range, the
distinction between (78) and (80) is retained since, in the general case,
g = g(V,
T) in (78) and
a a.
In practice, for certain minerals and for the present accuracy
of measurements,
Pth from (78) and the Mie-Grüneisen
theory
can be indistinguishable [Fei et al., 1992a, 1992b;
Mao et al., 1991],
especially for minerals with low Debye Temperature.
a.
In practice, for certain minerals and for the present accuracy
of measurements,
Pth from (78) and the Mie-Grüneisen
theory
can be indistinguishable [Fei et al., 1992a, 1992b;
Mao et al., 1991],
especially for minerals with low Debye Temperature.
The term
DPth in (77) can be approximated
in various
ways. For example, with given volume dependences of
K and
dT, by integrating (75), we can
find
t(V) at
T = constant
[O. Anderson et al., 1992a, 1993].
The temperature
dependence of
t is derived from data on
a(T) and
KT(T) at
P = 0. Another possibility to explicitly
approximate the thermal pressure is given by the power law for
t(V) on an isotherm.
and
dT, by integrating (75), we can
find
t(V) at
T = constant
[O. Anderson et al., 1992a, 1993].
The temperature
dependence of
t is derived from data on
a(T) and
KT(T) at
P = 0. Another possibility to explicitly
approximate the thermal pressure is given by the power law for
t(V) on an isotherm.
Fei et al. [1992a, 1992b] and
Mao et al. [1991] used a number of
models for
Pth in order to describe
P-V-T X-ray data.
Specifically, they assumed
( KT/
KT/ T)V = constant. Then, (70) yields
T)V = constant. Then, (70) yields
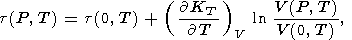 | (81) |
where
t(0, T) is determined from data on
a provided
that
(dKT/dT)P = constant,
the condition assumed over the entire
P-V-T range of measurements. From the assumption that both
temperature derivatives of
KT are constant, it follows that
tK = const. However, in such a case,
K
= const. However, in such a case,
K will increase
with pressure along an isotherm and decrease with temperature
along an isobar--the behavior that disagrees with the usual
properties of this parameters (see section 6). Note that the
estimated
dT values can be very sensitive
to the adopted
model of
Pth [e.g., Mao et al., 1991],
although the
Pth values themselves from various models can be close.
will increase
with pressure along an isotherm and decrease with temperature
along an isobar--the behavior that disagrees with the usual
properties of this parameters (see section 6). Note that the
estimated
dT values can be very sensitive
to the adopted
model of
Pth [e.g., Mao et al., 1991],
although the
Pth values themselves from various models can be close.
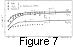 Finally, in Figure 7, we illustrate the temperature dependences of
t at
P = 0, calculated from the Mie-Grüneisen
EOS for
periclase, corundum, and forsterite, described in section 6,
with various values of
q in the interval 0-2. Although this
type EOS gives correct orders of magnitude and the
correct regularities in the
P-T variations of
t, it is
difficult to achieve the complete consistency for all of the
data given, as well as in the cases of specific heat (section 7)
and thermal expansivity (section 6). A better accuracy of the
EOS is undoubtedly required than that of the Mie-Grüneisen
EOS
in order to describe experimental data, to reliably predict
unmeasured properties, and in particular, to calculate the
phase diagrams at high pressures (when a 10% error in
Pth can
substantially affect the estimated phase boundary
slopes and positions).
Finally, in Figure 7, we illustrate the temperature dependences of
t at
P = 0, calculated from the Mie-Grüneisen
EOS for
periclase, corundum, and forsterite, described in section 6,
with various values of
q in the interval 0-2. Although this
type EOS gives correct orders of magnitude and the
correct regularities in the
P-T variations of
t, it is
difficult to achieve the complete consistency for all of the
data given, as well as in the cases of specific heat (section 7)
and thermal expansivity (section 6). A better accuracy of the
EOS is undoubtedly required than that of the Mie-Grüneisen
EOS
in order to describe experimental data, to reliably predict
unmeasured properties, and in particular, to calculate the
phase diagrams at high pressures (when a 10% error in
Pth can
substantially affect the estimated phase boundary
slopes and positions).
This document was generated by TeXWeb
(Win32, v.1.0) on February 10, 1999.
 20-22 g/mole
for mantle minerals, the
classic value of
CV for them is 1.13-1.25 J/g K.
Depending on mineral, the high-temperature anharmonic
corrections to
CV become singnificant either near the melting
point or even at room temperature (sometimes, at
T equal 1/6 of
the melting point) [Mulargia and Boschi, 1980;
Quareni and Mulargia, 1988;
Reynard et al., 1992;
Fiquet et al., 1992].
20-22 g/mole
for mantle minerals, the
classic value of
CV for them is 1.13-1.25 J/g K.
Depending on mineral, the high-temperature anharmonic
corrections to
CV become singnificant either near the melting
point or even at room temperature (sometimes, at
T equal 1/6 of
the melting point) [Mulargia and Boschi, 1980;
Quareni and Mulargia, 1988;
Reynard et al., 1992;
Fiquet et al., 1992].
 2E/
2E/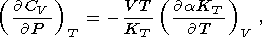
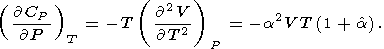
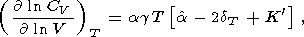
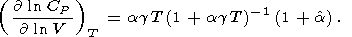
 .
. 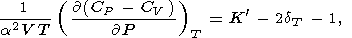
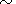 4 and
agT
4 and
agT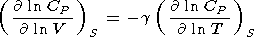
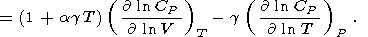
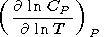
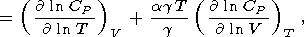
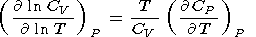
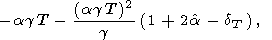
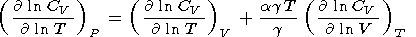
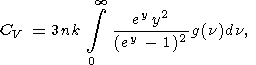
 300 K
(labelled
Qth ), on average, exceeds
the acoustic
300 K
(labelled
Qth ), on average, exceeds
the acoustic 10-3 ( T = 300 K) and
0.91
10-3 ( T = 300 K) and
0.91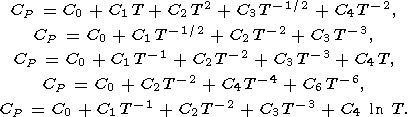

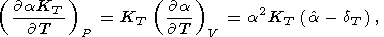
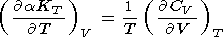
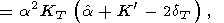
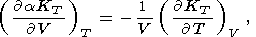
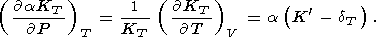
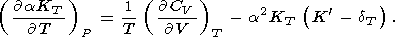
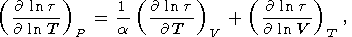
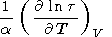
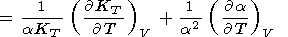
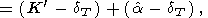
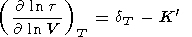
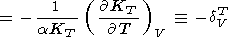
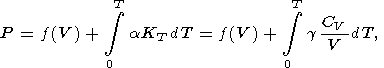
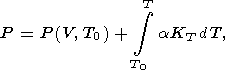
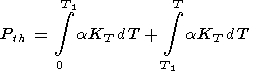
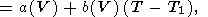
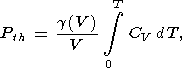
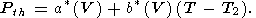
 (V)
in some temperature range, the
distinction between (78) and (80) is retained since, in the general case,
g = g(V,
T) in (78) and
a
(V)
in some temperature range, the
distinction between (78) and (80) is retained since, in the general case,
g = g(V,
T) in (78) and
a