2 V/ T P = 2 V/
P T that [Birch, 1952]
It follows from the identity
2 V/ T P = 2 V/
P T that [Birch, 1952]
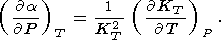 | (30) |
This fundamental relation is written in the dimensionless form
 |
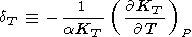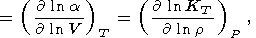 | (31) |
where the isothermal Anderson-Grüneisen parameter dT is introduced [O. Anderson, 1966a, 1967; Barron, 1979].
The variation of a with temperature at P = const is characterized by the parameter a Fürth, 1944; O. Anderson, 1966b; Birch, 1986; O. Anderson et al., 1993]
 |
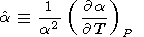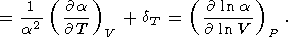 | (32) |
The term
 |
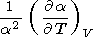can be related to the derivatives of
CV and
KT,
by making use of the identity
2S/ V T = 2 S/
T V, which leads to
 |
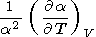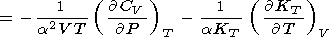 | (33) |
 |
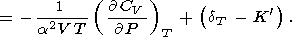Similarly, the identity
2S / P
T = 2S /
T
P yields
 |
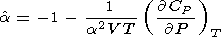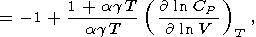 | (34) |
where the convenient dimensionless product is used
 |
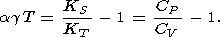Birch [1952] pointed out that parameter
dT for various
materials usually lies between 4 and 8 (at normal conditions),
which was borne out by subsequent studies
[see, e.g., Sumino and O. Anderson, 1984;
O. Anderson et al., 1992a]
some exclusions are also encountered: e.g.,
dT
1 for
KMnF
3 and
dT 77 for Re
2 O
3.
The parameter a values at normal conditions are commonly greater than the dT values [Birch, 1952; O. Anderson et al., 1992a]. The data and estimates listed in the tables of Pankov et al. [1997] for 25 minerals fall into the range 10 a 270. However, at high temperatures ( T > Q ), the dT and a values become closer to each other, and their concidence would mean that a were dependent only on volume (i.e., the intrinsic anharmonicity were suppressed).
The following three assumptions and their consequences are of interest:
(1) The specific heat CV is independent of pressure, i.e., CV = CV(T), as in the Van der Vaals or Hildebrand EOS's [O. Anderson, 1979a], or alternatively, CV = const, as in the classical limit at T > Q. Then, from (32) and (33),
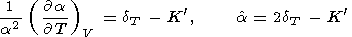 | (35) |
At
P = 0,
dT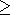
K
is the common case.
(2)
KT depends only on volume; the
KT(V) approximation is
often warranted at
T > Q [O. Anderson, 1982;
D. Anderson, 1988, 1989].
Then,
( KT/ T)V = 0,
and from (29) and (31), we have
K = dT;
i.e.,
dT either depends
only on
volume or is a constant (leading to the Murnaghan EOS (44)).
(3) If both conditions (1) and (2) take place, then
a = a(V)
and
K = dT
= a (that is either volume-dependent
or a constant).
In most of the interiror of the Earth, T > Q and a minimally depends on temperature. Consider a few approximate relations for evaluating the isothermal or adiabatic variation of a.
By using the general EOS form of (28) and the formula (12), we find the expansion for a
 |
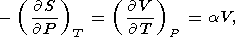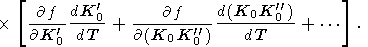 | (36) |
If only two first terms are retained in (36), then the formula of Birch [1952, 1968] derives. It should be noted that a in this formula changes its sign at KT/P = dT0 (the condition that may be achieved in the lower mantle at KT/P = 4.7 ). Moreover, in this case, dT given by most of the type (28) EOS's increases with pressure instead of its usual decrease (see section 9). It was shown, however, that such a change in the a sign is forbidden thermodynamically [Pankov, 1992].
As an example of using (36), we calculated a(P/K0) with the help of the EOS form proposed by Ullmann and Pankov [1976, 1980], for which
 |
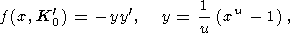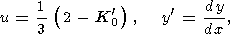 | (37) |
so that
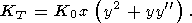 | (38) |
First, we set
dK0/ T = 0 and neglect terms containing
K0,
K0,
. The
a/a0
versus
P/K0 curves, obtained for
resonable values
K0
= 3 and 4 and
dT0 = 2, 4, and
6,
are shown in Figure 1. For change from
P to volume, Figure 2 gives
the variation of
P/K0 with
x. We see, in particular, that
the
dT0 values significantly
affect the estimated
a under lower-mantle conditions (at the base of
the
mantle compressed along its "hot" adiabat,
x 0.7 and
P/K0
0.70 for
K0 1.9-2.0
Mbar and
K0
= 3.8-4.1 [D. Anderson, 1989]). Furthermore, the
approximation used for
a may lead to the nonrealistic result
a< 0 within
the lower mantle.
To illustrate the influence of the non-zero
dK0/ T values,
now we allow for the third term in (36), with the setting
dK0/ T = 
2
10-3 K
-1 (the values that we estimated for NaCl
from data discussed by Birch [Birch, 1978]). The value
2 10-3 K
-1 is not realistic since it results in the increase of
a with pressure (Figures 1 and 3). On
the other hand, the
negative value
-2 10-3 K
-1 is too small, since it considerably
lessens the pressure at which the condition
a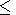
0 mentioned
above is reached.
The approximations
K = dT
(see above) and
dT constant at
T > Q imply a very weak temperature
dependence of
K. The lattice
dynamics models show
that
K for
MgSiO
3 perovskite varies less than 10%
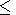in the temperature range of 300-2000 K ( dK0/ T 2 10-4 K
-1 ). The theoretical PIB model for MgO
[Isaak et al., 1990;
O. Anderson et al., 1993] shows that
dK0/ T somewhat increases
with temperature in the same interval of 300-2000 K, with the
values ranging, on average, from
2.8 10-4 to
4.2 10-4 K
-1.
Values of a similar order follow from the approximation
d ln K0/d
lnr = -1 indicated by D. Anderson
[1989] for PREM.
The derivative
dK0/d
T can also be estimated by the
approximation
KT = KT(V)
(i.e.,
K = dT
and (70) are
allowed for) noted above
 |
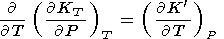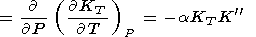 | (39) |
where the primes indicate pressure derivatives. With
a 3 10-5 K
-1 and
-KTK 5-10 [e.g., Pankov and Ullmann, 1979a;
Hofmeister, 1991b], we find
dK0/ T (1-3) 10-4 K-1, which is
close to the estimates found above.
Finally, we can use identity (91) from section 9, which
of course leads to (39) for
K = dT
(see (71)). Although
the terms in (91) are close to each other, the reasons given
below justify the inequality
(dT/ P)T 0,
and consequently,
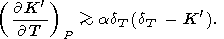 | (40) |
Substituting the parameter values from Tables 2 and 3 (see also tables in Pankov et al. [1997]) into the right side of the above, we find
 |
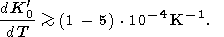It should be emphasized that the correction to
a in (36)
related to this derivative enables us to avoid negative
or increased values of
a at high pressures. The effect of
the value
dK0/dT
= 2 10-4 K
-1 on the
a curve for
K0
= dT0 = 4 is
shown in Figure 1.
O. Anderson [1967] derived the power law
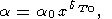 | (41) |
by integrating (30) and (8), provided that
 |
which yields
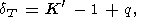 | (42) |
where parameter q is defined as
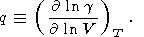 | (43) |
Moreover, he assumed that
dT K const.
The constancy of
K (or alternatively,
K = K(T) ) leads to the
Murnaghan EOS (of a type of (28))
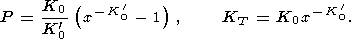 | (44) |
It is clear that (41) simply follows from the definition of dT by (31) on the condition that dT is either only temperature-dependent, dT = dT(T), or is a constant; moreover, (44) can be replaced with any suitable approximation to the isotherm P(V, T0).
The two functions
a(V, T) and
P(V, T), however,
cannot be picked independently. For example, the EOS can
apparently be defined by specifying
a(V, T) and
P(V, T0).
At this point, it is appropriate to discuss the
following generalization of the results mentioned in various
papers
[Birch, 1968;
Clark, 1969;
O. Anderson, 1986;
D. Anderson, 1989]. Consider four statements:
( 1) the Murnaghan
EOS (44) is valid, where it is assumed that
K0 is a function
of temperature,
K0(T), and
K0
is either a constant or
depends only on temperature; ( 2)
(dT/ P)T = 0
(i.e.,
dT = const or
dT = dT(T) );
( 3)
( K/ T)P
= 0 ; ( 4)
dT = K that, according to (71), is equivalent
to
KT = KT(V)
(i.e.,
t(T) = aKT
or
t = const).
Then, by making use of identities (44), (71), (91), and (92), it
can be proved that, if any two (except the pair ( 1) and ( 3))
of the four statements above hold true, then the other two
statements are also valid. Moreover, then
dT = K =
const and (44) always takes place. If, in addition to these two
statements, it is assumed that
CV = const or
CV = CV(T),
then we have
a = a(V),
K = dT
= a = const and
t = const (see section 6.1 and (69) and (71)).
It is clear that such statements place constraints on the EOS
formulation. For example, when an equation of type (28) is
accepted instead of the Murnaghan EOS, only one of the above
statements can strictly be true. Specifically, the concurrent
use of the Birch-Murnaghan EOS and the assumption
dT = dT(T)
(or
dT = const) is
incompatible with the
condition
dT = K or
K = K(P).
Another not obvious inference is that the Murnaghan equation (44) uniquely follows from the assumptions KT = f(P) + aT ( a being a constant) and t = t(T) or const.
It is interesting to consider the use of the Murnaghan formula as the potential (lattice) part of the P-V-T EOS in the classical high-temperature approximation. In general, for CV = const, we have a linear dependence of KT(V, T) on T (see (69) and (70)), and only for g/x = const ( q = 1 ) and the Murnaghan potential, we obtain
where
a,
b, and
c are constants ( K = const).
Hence, it is
seen that all isotherms
(T 0) are also represented by formula
(44), but for a nonlinear
g (x) behavior, this is,
strictly speaking, not the case.
The consideration presented above concerns also the Birch's law,
which for minerals with the mean atomic mass of
m = 20-22
g/mole can be written in the power form
KT = aVb
(where
a and
b are constants and the distinction between
KS and
KT is neglected). Since here
K = const and
KT = KT(V)
and
(44) is used, this law gives rise to
dT = K = const,
formula (41), and for
CV = const,
a = a (V).
Figure 1 shows the behavior
a determined by (41), where
the EOS is found by (37) with
K0
= 3 and 4 (the respective
a curves pass through the ends of the bars in
Figure 1).
The original assumption of O. Anderson [1967] dT = const was justified by the ultrasonic and shock-wave data of that time and was seemingly corroborated by later ultrasonic and resonance measurements [O. Anderson et al., 1990; Chopelas and Boehler, 1992]. In particular, based on data for seven minerals, the value of dT = 4-6 was recommended to be representative of the lower mantle. However, analyzing seismological and geoid data, D. Anderson [1987, 1989] found dT = 2-3 for in situ lower-mantle conditions. The assumption can therefore be made that dT must decrease with pressure. Evidence for this can also be found in shock-wave and static compression data [Birch, 1986; O. Anderson et al., 1993].
Ab initio calculations for MgO by Reynard and Price [1990]
give
a constant value in the range
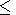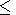0.7 x 1.0.
Another ab initio
results [Isaak et al., 1990] reveal, however, that
dT actually decreases
by decreasing
x.
To determine the a (x) more accurately than given by the power law (41), Chopelas and Boehler [1992] used data on the adiabatic pressure gradient tS and specific heat CP. From the Maxwell relation (14), they derived
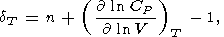 | (45) |
where
n
(
ln tS/ ln V)T.
Then, they set
n = mx, where
m = 6 1 from
measurements for weakly compressible materials, and
( ln CP/
ln V)T
= 1 or 0
for
T < Q or
T > Q, respectively (compare with
the data listed in Table 3 and the paper by
Pankov et al. [1997]).
Thus, the Chopelas and Boehler' formula for
a can be written in the form
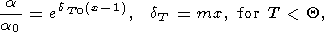 | (46) |
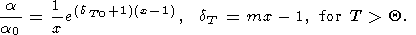 | (47) |
O. Anderson et al. [1992a, 1992b, 1993] favored the power law dT = dT0xk (for T Q ) that yields
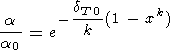 | (48) |
with only small deviation from values by (47). The value of k = 1.1-1.4 in (48) was inferred from the theoretical PIB model of Isaak et al. [1990].
Applying (47) or (48) to the lower mantle, we find that
a decreases 4-5 times along the "hot" lower-mantle
adiabat, from
the state
P = 0 and
T 1700-2000 K to the base of the
mantle. The power law (41) with
dT = 5-6 gives
a greater
decrease in
a (6-8 times), and the same law with
dT = 2-3 results
in a smaller decrease of
a (2-3 times). Although approximations (47) and
(48) are more
preferable than (41), they require additional confirmation and
information on parameters
m,
k, and
( ln CP/ ln V)T.
a in the lower mantle by (36) and
(37), as described in section 6.2.1, with
dK0/d
T = 2.3 10-4
K-1,
gives the results close to those derived from (47) or (48)
(Figure 3).
Similar results for a with dT decreasing under compression were obtained by Zharkov [1997] from his analysis of EOS's at extremely high pressures. Still earlier, Zharkov [1959] showed that the lower mantle thermodynamics quantified on the basis of the Debye model and seismic data gives the 4-5-fold decrease in a at the mantle base compared to the value at P = 0.
To this point, considering
a at high compression,
we have not applied to the Grüneisen parameter
g.
However, the problem of thermal expansivity at high pressures
and temperatures is intimately related to the problem of a
similar variation of the Grüneisen parameter.
D. Anderson [1987, 1989]
characterized the lower-mantle thermodynamics by
using the acoustic or Brilloin
g. For the adiabatic
lower mantle, he found from PREM that
g0 = 1.4 and
a0 = 3.8 10-5 K
-1 at
P = 0 and
T = 1700 K;
the value of
g was determined by the thermodynamic relation
(8) for
CV = const ( T > Q ). Given function
g (V), the
variation of
a with volume in the classical temperature
range can be evaluated by the formula derived from (8)
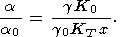 | (49) |
Note that the thermodynamic parameter g, generally speaking, is different from the so-called lattice Grüneisen parameter [e.g., Mulargia, 1977; D. Anderson, 1989; O. Anderson, 1968, 1979b, 1980]. However, assuming that the latter depends only on volume, both parameters were found to coincide (the same inference follows from the quasiharmonic atomistic model of EOS at high temperatures, when, on the other hand, we come up with the purely thermodynamic consequence g = g (V) for CV = const (see section 11).
The three most familiar formulas for the lattice g can be written in the general form [Zharkov and Kalinin, 1971]
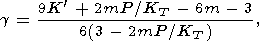 | (50) |
where m = 0, 1, or 2 gives the formulas of Slater, Dugdale-Macdonald, and Zubarev-Vashcheno (or Irvine and Stacey [1975]), respectively. The latter of these formulas appears to be the most favored, at least at T > Q, for high symmetry crystals. Following Leibfried and Ludwig, 1961], g can approximately be expressed in terms of the root-mean-square frequency of atomic oscillations. For cubic crystals with the central interaction, when only the nearest neighbors are allowed for, this approximation also leads to the Zubarev-Vashchenko formula [Pankov, 1983; Hofmeister, 1991a].
Calculation by (50) requires knowledge of the
P(V) dependence
at
T = 0 K, but the replacement of the
T = 0 K isotherm by any
isotherm at
T > 0 K is not significant for this case. Using the
EOS from (37) at
K0=4
and determining
g by (50) at
m = 2 and then
a by (49), we obtain
a0/a
= 1.7
for
x = 0.7 (that is approximately at the mantle base).
Such a small decrease in
a compared to the 4-5-fold
decrease found above is due to the fact that the EOS by (37),
like many other
P(V) relationships
[Pankov and Ullmann, 1979b],
results in a low value of the slope
 |
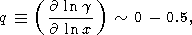calculated from (50). This either tells us that a more
flexible EOS involving the independent parameter
K0K0 K2 (such as in model 2 by
Ullmann and Pankov [1980] or the
Birch-Murnaghan fourth-order EOS) must be introduced, or some
amendments to (50) are required. The Zubarev-Vashchenko formula
was somewhat improved by Stacey [1981, 1992],
but nevertheless, the slope
q for most two-parametric
( K0 and
K0 )
EOS's
appears to remain low).
Another useful approximation for g is the empirical power law [e.g., O. Anderson, 1968, 1974; McQueen et al., 1970]
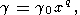 | (51) |
where
q is often assumed to be one, according to shock-wave
data [McQueen, 1991] or studies of the mantle
[O. Anderson, 1979b;
D. Anderson, 1989]. From (49) with
q = 1, we find
Birch's formula
aKT = a0K0
= const, which gives
a0/a
= 3.5-4.0 at the mantle base (for
x = 0.7,
K0
= 4,
KT/K0 =
3.51, and
T = 2000-3000 K). The value
of
q = 1.5-2.0 may be more favored for the mantle perovskite
[Pankov et al., 1998], yielding, however,
a0/a
= 4.2-5.0 that is close to the result obtained from
(47) and (48).
Note that, according to (49), the assumption of the power laws for a (41) and g (51) again gives the Murnaghan EOS (44). Since the latter fits data well over a range of P/K0 0.3 ( x 0.82 ), we expect (41) to be a sufficient approximation for a in the same compression range.
Duffy and Ahrens [1993] estimated
a from shock wave
data for MgO, CaO, CaMgSi
2 O
6 and
e -Fe at pressures to
P > 140 GPa. By using (49) and (51) with
q = const and
KT/K0 from
the PIB model for MgO [Isaak et al., 1990],
they found
q = 0.5 0.5 that is smaller than
q = 0.83-1.26 in the
compression range
x = 0.67-1.0 along the PIB isotherm.
Periclase is more compressible than the lower mantle matter and
has
x = 0.67 at
P = 134 GPa near the mantle base (according to
the PIB 2000 K isotherm of MgO,
P/K0 = 1.047,
KT/K0 =
4.699,
and
K = 4.74 ).
With these values, the shock wave
results of Duffy and Ahrens for MgO give
a0/a
= 3.1-4.7
at the mantle base ( x = 0.67 ), i.e., the value 1-1.6
times less than
a0/a
by (47) and (48) at the
typical value of
dT0 = 5 1 (if the value
dT0 = 4 is used
in (47) and (48), the resulting
a0/a
value will be closer to the shock-wave
estimate above). These results can be viewed as an argument for
the decrease of both
dT and
q under compression.
In analysis of the volume dependence of g, O. Anderson et al. [1993] proposed the power law
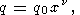 | (52) |
which, similarly to (48), yields
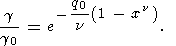 | (53) |
Setting q0 = 1.5-2.0 and n = 1 (as for MgO, according to O. Anderson et al. [1992b]), we find from (49) that a0/a = 4-4.5 at x = 0.7. Note that q0 for MgO descends from 1.72 to 1.26 as temperature increases from 300 K to 2000 K [O. Anderson et al., 1993].
In total, many estimates of a0/a using various methods described above consistently show that the thermal expansion coefficient in the lower mantle decreases 4-5 times along the hot low-mantle adiabat as the pressure increases from zero to the base of the mantle. Nevertheless, the complete consensus on all the parameter values related to these estimates (e.g., for q and dT ) has yet not been achieved.
Most data on thermal expansion refers to the dependence a(T) = a0 at P = 0. The value of a0 is necessary, in particular, to extrapolate the thermal expansivity data to higher pressures in the mantle. The typical behavior of a(T) is illustrated in Figures 4 and 5. Usually, the data at P = 0 are fitted using the empirical formula [e.g., Fei et al., 1990, 1991]
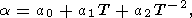 | (54) |
which we used to calculate a presented in Table 2 (and in Pankov et al. [1997]). Note that the applicability of (54) can also be justified by calculations of phase diagrams [Fei et al., 1990, 1991].
A theoretically based approach to calculating a(T) was developed by Suzuki [1975a, 1975b], who used the Mie-Grüneisen EOS yielding
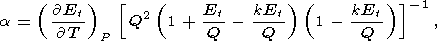 | (55) |
where Et is the Debye thermal energy
 |
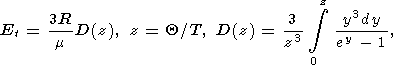k = 1/2(K0-1),
Q = K0V0 / g, and
D(z) is the Debye function.
Here, it is assumed that
g = constant, and
parameters
K0 and
K0
are defined at
T = 0. The fitted
parameters are
Q,
k, and
Q. Formula (55) is derived
by expanding the potential pressure in
V and truncating at only
two first terms. The
Q values obtained from this method
are given in Table 2 (see also Pankov et al. [1997]).
O. Anderson et al. [1992a] extrapolated
a0(T) from a
fixed value at
T
> Q
to higher temperature using the
relation
 | (56) |
where dT = a = constant (see (32)). Formula (56) is easily derived from the condition that a0 at P = 0 varies with density by the power law. Note that (56) has an asymptote close to which a dramatically increase with temperature (reflecting to some extent the fact that the potential energy has an inflection point).
For a more complete consideration of the temperature
behavior of
a, we calculated
a(T) for three
minerals from the Mie-Grüneisen EOS (with
the Debye model), in
which, unlike the Suzuki method,
g(x) was found by (51)
with
q = 0, 1, and 2, and room-temperature isotherms were
represented by equations (28) and (37). The material parameters
of the EOS's were found from values of
r,
KS,
a,
CP, and
( KS/ P)T at
normal conditions (Tables 2 and
3).
The results of the computations are shown by the solid lines in Figures 4 and 5. We see that the curves for periclase and particularly forsterite systematically deviate from the experimental points at high temperatures, although there is a considerable uncertainty in data for a at high temperatures. Nevertheless, such deviations can be caused by the fact that the temperature dependence of g (at V = const) is not accounted for in the Mie-Grüneisen EOS [Mulargia, 1977; Mulargia and Boschi, 1980; Mulargia et al., 1984; O. Anderson et al., 1992a; Molodets, 1998]. To gain a better insight into the quality of the Mie-Grüneisen EOS and to construct a self-consistent database on EOS parameters, it is very important to measure the thermal expansivity of minerals at high temperatures, up to their melting points. This conclusion was emphasized by many authors [e.g., Saxena, 1988, 1989; Goto et al., 1989; Isaak et al., 1989b; Gillet et al., 1991; Richet et al., 1992].
