Реперы температуры в литосфере, соответствующие фазовым превращениям вещества, и возможности определения глубины их залегания

В. С. Якупов, С. В. Якупов

Институт горного дела Севера СО РАН, Якутск

Содержание

Аннотация

Проблеме исследования теплового состояния недр Земли посвящено множество работ, в том числе в рамках крупных международных проектов. Представления об изменении температуры с глубиной, оцениваемые "в высокой степени неоднозначными'' [Любимова, Фельдман, 1975], основаны на общих физических соображениях и косвенных данных. Обычно решается задача теплопроводности для представляющейся конкретному автору наиболее вероятной в данный момент модели строения земной коры и верхней мантии Земли при различных допущениях. Расхождение между результатами расчетов по разным моделям для литосферы в среднем порядка 100% (от наименьшего). Другой вариант предусматривает использование устанавливаемого методами МТЗ, МВЗ и другими методами электромагнитных зондирований с контролируемыми источниками поля распределения электропроводности горных пород с глубиной и сопоставление его с результатами экспериментальных исследований зависимости электропроводности от температуры и давления. Наиболее детально разработанные модели нормального (стандартного) геоэлектрического разреза на основе данных магнитотеллурического зондирования [см. Ваньян, Шиловский, 1983; Жамалетдинов, 1990] предполагают плавное увеличение электропроводности вещества с глубиной и изменение на внутренних границах раздела лишь ее градиента. И здесь степень неопределенности такова, что различие моделей разных авторов по электропроводности достигает одного-двух порядков. Еще одна обсуждающаяся возможность оценки распределения температуры в земной коре заключается в определении методами геофизики температурных реперов - положения границ, на которых по достижении температуры фазового перехода в каком-либо из компонентов горной породы или заполняющем ее поровое пространство растворе (в общем случае флюиде) происходит фазовый переход, сопровождающийся изменением какого-либо из физических свойств породы. В частности, можно указать переходы воды в лед и надкритическое состояние, частичное плавление горных пород (базальта) в астеносфере, превращение ферромагнетиков в парамагнетики при достижении температуры точки Кюри, переход оливина в шпинель и др. Трудность заключается в том, что, например, температуры перехода воды как в лед, так и в надкритическое состояние [Смит, 1968] зависят от состава и концентрации растворенных в ней веществ и давления. Того же рода неопределенность в силу ряда причин имеет место в случае зоны частичного плавления в астеносфере и в зоне перехода оливина в шпинель. Температура этого фазового перехода в предположении Fe/(Fe + Mg) 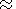0,1 в соответствии с гипотезой пиролитового состава мантии Земли при давлении 135 кбар равна 1600^o 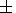50^o С [Жарков, 1978]. Она будет уже иной в случае отклонения состава оливина от указанного. В работе С. Акимото и Х. Фуджисава [Akimoto and Fujisava, 1965] температура фазового перехода оливина в шпинель при давлении 43,8 кбар была определена равной ~1170^o C. Отсюда очевидно, что в общем случае речь может идти только об оценке температуры конкретного фазового перехода сверху или снизу. Важен также характер изменения изучаемого свойства породы при фазовом переходе: скачком, как следует из общей теории фазовых превращений, или на отвечающей ему границе раздела меняется градиент изменения данного свойства с глубиной, как, например, это принимается для верхней границы астеносферы [Ваньян, Шиловский, 1983].

Из числа указанных температурных реперов широко использовались нулевая изотерма по мощности мерзлых горных пород [Калинин, Якупов, 1989; Якупов, 2000] и изотерма точки Кюри магнетита - наиболее широко распространенного в литосфере ферромагнетика [Петрова и др., 1976] - по глубине залегания нижней кромки намагниченных тел [Булина, 1961, 1970; Волк и др., 1977а, 1977б]. На границе талых и мерзлых горных пород, как правило, скачком меняются электропроводность, диэлектрическая проницаемость и, в случае грубозернистых рыхлых отложений и грубокластических скальных пород, скорость распространения сейсмических волн или, в общем случае, электрический и акустический импедансы. Области с пресными и солеными подмерзлотными водами могут быть разделены по отсутствию или наличию стохастической связи между мощностью толщи мерзлых горных пород и проводимостью подмерзлотного горизонта [Калинин, Якупов, 1989]. Таким образом, в области существования мерзлых толщ с пресными подмерзлотными водами положение первого из указанных реперов температуры - t = 0^o С - при благоприятных на то условиях вполне надежно устанавливается методами электроразведки: средняя относительная погрешность определения равна ~10%. Эту задачу удалось решить и для одной из крупнейших гидрогеологических структур с солеными подмерзлотными водами - Оленекского артезианского бассейна. Для него получено уравнение регрессии температуры на нижней границе мерзлых горных пород на их мощность [Калинин, Якупов, 1989]. Определение положения точки Кюри по нижней кромке субвертикальных однородно намагниченных пластов в лучшем случае, по оценкам на простейших моделях, может быть выполнено со средней погрешностью ~30%; нередко решение задачи оказывается неоднозначным [Страхов, Лапина, 1976].

Рис. 1

Другая трудность заключается в том, что на первый взгляд неясен характер изменения конкретного физического свойства вещества при фазовом переходе. Можно предположить следующие схемы поведения удельного электрического сопротивления с глубиной вблизи границы раздела, образованной фазовым переходом в какой-либо из составляющих горной породы, и на ней (рис. 1). Простейший вариант (рис. 1а) имеет место, например, для изменения удельного электрического сопротивления на нижней границе литологически однородной мерзлой толщи с пресными подмерзлотными водами, т.е. при температуре, равной нулю, [Якупов, 2000] или магнитной проницаемости ферромагнетиков при температуре точки Кюри. На больших глубинах электропроводность горных пород с ростом температуры растет. Предполагается, что с образованием зоны частичного расплава в астеносфере ее электропроводность с глубиной начинает расти быстрее и, таким образом, верхней ее границе соответствует резкое (скачкообразное) увеличение градиента электропроводности [Ваньян, Шиловский, 1983] - это наиболее сложный случай (рис. 1г). Рассмотрим этот случай в силу его общности подробнее, привлекая теорию фазовых переходов вещества и идеи теории протекания. Зона частичного расплава в верхней части астеносферы возникает из-за плавления одного из компонентов породы - базальта. Доля расплава (по оценке Рингвуда от 2 до 30% объема [Рингвуд, 1981]) считается возрастающей с температурой, т.е. с глубиной. Однако известно, что при прочих равных условиях любой фазовый переход конкретного вещества из одного состояния в другое происходит при постоянной температуре. В случае большой плотности теплового потока, т.е. достаточно быстрого нагревания или охлаждения, возможно образование переходной зоны, в которой сосуществуют обе фазы - твердая и жидкая. В глубоких горизонтах литосферы, если исключить случаи возникновения магматических очагов в областях активной вулканической деятельности, это явление не имеет места: тепловое состояние литосферы можно рассматривать как квазистационарное. Отсюда зона частичного расплава в астеносфере неизбежно имеет сверху четкую границу раздела, на которой часть ее физических свойств меняется скачком. В ее пределах с глубиной меняются давление и температура и вследствие этого, например, электропроводность, но не доля расплава, во всяком случае для двухкомпонентной среды. Рассмотрим электропроводность на границе зоны частичного расплава и по обе ее стороны с позиций теории протекания. Горные породы нижней части литосферы и далее астеносферы являются поликристаллическими образованиями, расположение отдельных компонентов в которых хорошо соответствует плотной упаковке случайным образом распределенных их частиц разного размера и формы. Тогда электропроводность g такой трехмерной системы достаточно большого объема описывается формулой

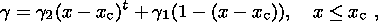(1)

где g₁ - электропроводность астеносферы над зоной частичного расплава; g₂ - электропроводность расплава; x - содержание расплава в относительной мере от 0 до 1; x _c - его пороговое значение, при котором возникает протекание по расплаву, равное в нашем случае 0,25; t - критический индекс электропроводности. Формула (1) верна в качестве первого приближения, с точностью до сомножителя для g₁ и g₂ [см. Эфрос, 1982] (нас интересует характер поведения электропроводности породы вблизи и на пороге протекания по расплаву). Если учесть извилистость скелета бесконечного кластера по расплаву, доказанную для трехмерных сред, то t = 1 + n, где n - индекс радиуса корреляции, равный 0,8-0,9. Добавим, что при образовании бесконечного кластера gg₁. В результате получим

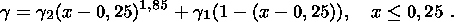(2)

Рис. 2

На рис. 2 изображен график изменения логарифма электропроводности системы как функции температуры, на котором точками указаны также значения logg = f(x) в соответствии с формулой (2). Подчеркнем, что далее с глубиной электропроводность меняется, следуя изменениям давления и температуры: доля расплава в образовавшейся двухфазной системе остается постоянной и может измениться (скачком!) только в случае начала плавления другого компонента вещества астеносферы. Таким образом, на границах раздела, образованных фазовыми переходами вещества с достижением порога протекания, имеет место скачкообразное изменение по крайней мере части физических свойств вещества и в наиболее сложном случае, если говорить об электропроводности, функция g = j(z) вида, изображенного на рис. 1в. Такое, с четко выраженными границами раздела (рис. 1а, б, в), изменение электропроводности горных пород литосферы с глубиной уже заметно упрощает интерпретацию данных МТЗ, МВЗ и зондирований с контролируемыми источниками поля. Кроме того, становится принципиально возможным использование радиолокации, дело лишь за техническими средствами. Главные направления можно указать сразу: применение для создания импульсных электромагнитных полей мощных МГД-генераторов [Велихов, Волков, 1982]; использование в качестве изучаемого параметра напряженности магнитного поля; использование в качестве приемного устройства для определения времени прихода отраженных волн высокоточных магнитометров на основе эффекта Джозефсона. Это позволит резко повысить точность определения глубины залегания рассматриваемых границ раздела. Главной частью погрешности построения функции изменения температуры t с глубиной t = f(z) станет определение температуры конкретного фазового перехода вещества, которая зависит от содержания других компонентов породы и давления. Она точно известна для замерзания свободной пресной воды в поровом пространстве горных пород и фазовых переходов второго рода с превращением ферромагнитных минералов в парамагнитные, из которых представляют интерес магнетит и пирротин. В других случаях речь будет идти об оценках температуры фазового перехода снизу или сверху в зависимости от содержания летучих и прочих компонентов в породе и которые со временем будут несомненно уточняться.

Рис. 3

Рис. 4

Гипотетическая функция t = f(z) будет выглядеть примерно такой, как она изображена на рис. 3 в предположении, что все границы раздела, образованные фазовыми переходами вещества, удалось установить на одном участке или в сходных условиях. На рис. 3 точками показано положение границ раздела с известной температурой фазового перехода (вода - лед; пирротин, магнетит - парамагнетики). Горизонтальные отрезки на рис. 3 условно равны диапазону возможного изменения температуры конкретного фазового перехода: воды в надкритическое состояние, оливина в шпинель, плавление базальта; штриховыми линиями изображены оценки t = f(z) снизу, а пунктирными - сверху. В общем случае после образования расплава из одного из компонентов породы в результате его сегрегации, изменения содержания или соотношения некоторых компонентов породы, например, воды, давления, может начаться плавление другого компонента породы, затем следующего и т.д. Каждый раз при новом фазовом переходе в компонентах породы (имеется в виду их плавление) общий объем расплава будет возрастать скачком, а температура породы в целом до завершения очередного фазового перехода оставаться постоянной. Протекание по расплаву может наступить на одном из этих фазовых переходов, не обязательно на первом, что и отображено условно на рис. 4. Нижняя граница зоны частичного расплава, по-видимому, определяется исчерпанием относительно легкоплавких компонентов вещества астеносферы.

Порог протекания как константы транспортных процессов и порог механической связности в возникающей в результате фазового перехода системы могут не совпадать и тогда результаты определения положения границы раздела электрометрическими и сейсмическими методами будут различаться (см., например, [Якупов, 2000]). Если содержание новой фазы будет мало, то сохранится механическая связность исходной породы и, следовательно, ее однородность по связанным с ней параметрам.

Заключение

1. Положение границ раздела в литосфере, образованных фазовыми переходами в отдельных компонентах горных пород или заполняющих их поровое пространство флюидах, определяет расположение в ней реперов температуры. Для части фазовых переходов их температура известна, для других она зависит от соотношения или содержания других компонентов породы и давления.

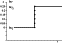
2.  На границах раздела, образованных указанными фазовыми переходами, часть физических свойств меняется и меняется скачком так, что для их распределения с глубиной имеет место один из приведенных на рис. 1 вариантов: а, б или в. Это позволяет определять положение этих границ раздела в случае достаточной их контрастности методами МТЗ, МВЗ и зондированиями с контролируемыми источниками поля, упрощая в целом интерпретацию полученных с их помощью данных и делая ее результаты более надежными. Теоретически для этой цели можно использовать метод радиолокации; технические средства для этого, пока еще ограниченные по своим возможностям, существуют.

3. Если содержание новой фазы достаточно велико, то границы раздела по протеканию и механической связности могут совпадать и тогда ее положение может быть определено и электрометрическими и сейсмическими методами. Если указанные пороги расходятся, но достигнуты, то расходятся и положения границ раздела по данным электрометрии и сейсмики: по данным электрометрии граница раздела будет залегать выше. Если порог механической связности не будет достигнут, то обусловленные ею физические свойства породы останутся неизменными.

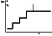
4. В результате реализации высказанных идей современные представления о распределении температуры в литосфере могут быть существенно уточнены (в виде, например, представленном на рис. 3).

Литература

Булина Л. В., Об использовании материалов аэромагнитной съемки для изучения глубинного строения земной коры в пределах Сибирской платформы, Советская геология, (5), 134-138, 1961.

Булина Л. В., Особенности пространственного распределения нижних кромок намагниченных образований консолидированной земной коры, Изв. АН СССР, сер. геол., (5), 40-47, 1970.

Ваньян Л. Л., Шиловский П. П., Глубинная электропроводность океанов и континентов, 86 с., Наука, Москва, 1983.

Велихов Е. П., Волков Ю. М., Перспективы развития импульсной МГД-энергетики и ее применение в геологии и геофизике, Глубинные электромагнитные зондирования с применением импульсных МГД-генераторов, с. 5-25, Апатиты, 1982.

Волк В. Э., Осипов В. А., Шимараев В. Н., Использование магнитометрических данных в исследовании земной коры Арктического шельфа СССР, Структура земной коры континентов и океанов, Труды ЛОЕ, вып. 2. с. 93-99, Л., 1977a.

Волк В. Э., Гапоненко Г. И., Зацепин Е. Н. и др., Изучение земной коры шельфа арктических и дальневосточных морей СССР по аэромагнитным данным, Проблемы геофизических исследований полярных областей Земли, с. 53-67, изд. НИИГП, Л., 1977б.

Жамалетдинов А. А., Модель электропроводности литосферы по результатам исследований с контролируемыми источниками поля, 159 с., Наука, Л., 1990.

Жарков В. Н., Внутреннее строение Земли и планет, 191 с., Наука, Москва, 1978.

Калинин В. М., Якупов В. С., Региональные закономерности поведения мощности мерзлых толщ, 142 с., Якутск, 1989.

Любимова Е. А., Фельдман И. С., Тепловой поток, температура и электропроводность земной коры и верхней мантии, Кора и верхняя мантия Земли, с. 144-190, Москва, 1975.

Петрова Г. Н., Печерский Д. М., Лыков А. В., Магнитные минералы и магнитные аномалии, Магнитные аномалии земных глубин, с. 55-63, Наукова думка, Киев, 1976.

Рингвуд А. Е., Состав и петрология мантии Земли, 583 с., Недра, Москва, 1981.

Смит Ф. Г., Физическая геохимия, 475 с., Недра, Москва, 1968.

Страхов В. Н., Лапина М. И., Неоднозначность решения обратной задачи магнитометрии, Магнитные аномалии земных глубин, с. 185-199, Наукова думка, Киев, 1976.

Эфрос А. А., Физика и геометрия беспорядка, 175 с., Наука, Москва, 1982.

Якупов В. С., Исследование мерзлых толщ методами геофизики, 316 с., ЯФ Изд. СО РАН, Якутск, 2000.

Akimoto, S., and Y. Fujisava, Demonstration of Electrical Conductivity Produced by the Olivin - Spinel Transition, J. Geophys. Res., 70, (2), 443-450, 1965.