
А. В. Каракин
ВНИИГеосистем, Москва
Многочисленные исследования [Григорьев, 1971; Смит, 1968; Файф и др., 1981] показывают, что вода подземных недр составляет единую подземную гидросферу. Объем вод (связанных и свободных) в коре соизмерим с объемом воды в мировом океане и составляет ~4% объема коры. Такое количество воды в коре оказывает значительное влияние на все геологические процессы в ней. Естественно ожидать, что наибольшие эффекты флюиды оказывают в трещиноватых, сильно проницаемых слоях, к которым относятся и коровые волноводы. Поэтому актуальность этой проблемы не вызывает сомнения.

|
| Рис. 1 |
Еще Гутенбергом [Gutenberg, 1959] было высказано предположение о существовании сейсмических волноводов в земной оболочке для глубин, соответствующих астеносфере. Впоследствии они были обнаружены в верхней мантии, нижней коре, а в рифтовых зонах - вплоть до поверхности Земли. Было высказано предположение, что слои низких скоростей связаны с переходом вещества в аморфное состояние [Магницкий, 1968] и частичное плавление [Теркот и др., 1985]. Эта точка зрения, общепринятая для астеносферы и объясняющая ее реологические свойства, распространялась и на кору. Однако в коре (в особенности, в ее верхней части) температуры слишком малы для наличия включений расплавов, рассеянных по большому объему. Поэтому изучались и другие гипотезы. В большинстве из них свойства волноводов связывались с различиями в литологическом составе пород, например, с наличием графитосодержащих пород. Гипотеза о литологическом происхождении волноводов наталкивается на ряд серьезных трудностей. Одна из них состоит в том, что вещество коры постоянно поднимается и опускается, перемешиваясь в складки и различные литологические несогласия. Между тем волноводы, как правило, выдерживаются на определенной глубине в горизонтальном положении. Это свидетельствует о том, что они скорее всего связаны с состоянием вещества, а не с его составом.
Сопоставление сейсмических [Краснопевцева, 1978; Сейсмические модели..., 1980] и геоэлектрических [Ваньян, 1984; Ваньян, Шиловский, 1983] данных показывает, что зоны пониженных скоростей и повышенной электропроводности в целом совпадают, хотя и могут иногда различаться. Накопленный с 60-тых годов экспериментальный материал заставляет склоняться к мысли о том, что на глубинах до 30 км наиболее вероятной причиной появления указанных зон является наличие в них электропроводящих флюидов [Ваньян, 1984]. Объемное содержание флюидов внутри слоев с повышенной электропроводностью достигает нескольких процентов [Ваньян, Шиловский, 1983; Feldman, 1976]. Нельзя исключить также такую ситуацию (которая наиболее вероятна в низах коры), когда в зависимости от теплового режима в качестве флюида в пористой структуре волновода попеременно находятся либо расплав, либо летучие (водные) флюиды.

|
| Рис. 2 |
Принципиально другая картина наблюдается в тектонически активных регионах, представленных на рис. 2e, f. Первый из них соответствует континентальной гранитной коре толщиной 30 км, находящейся в условиях растяжения или сдвига (Провинция Хребтов и Бассейнов на западе США или разлом Сан-Андреас). Здесь хрупкий, ослабленный слой находится на глубине 10-15 км. Если же в аналогичной ситуации кора расслоена на гранитный и базитовый слои, то появляются два минимума - на подошве гранитного и базитового слоев (рис. 2f).
При сильных сдвиговых деформациях в коре происходит разрушение в ослабленных областях с образованием трещиновато-пористой структуры волноводов. Так в общих чертах можно себе представить механизм образования волноводов. Однако обобщенная прочность является слишком общим и нечетким понятием, поскольку в действительности механизм разрушения сложнее. Поэтому уместно рассмотреть и другие схемы разрушения.

|
| Рис. 3 |

|
| Рис. 4 |
Коровые волноводы в данной концепции отождествляются с участком неустойчивого разрушения, который начинается на границе Форша и заканчивается на границе Конрада. Именно в этом случае возникает дилатансионный эффект, связанный с расширением порового пространства. В этой же области происходит расширение и выполаживание листрических разломов, что подтверждается различными геофизическими измерениями. Дилатансионное расширение создает вакуумный эффект засасывания жидкости [Nikolaevskii, 1990]. Следует отметить, что эта схема является весьма условной и достаточно грубой. Она не учитывает изменения направления и величины тектонических напряжений, влияние флюидов и динамики слоев. В частности, она не учитывает тот факт, что структура слоев в сильной степени зависит от их предшествующего состояния. Другими словами, она не учитывает то обстоятельство, что структура и свойства коры описываются эволюционными геомеханическими уравнениями, составной частью которых являются диаграммы состояния. Поэтому схему Николаевского можно рассматривать лишь как отправную точку рассуждений, претендующую на описание лишь самых общих закономерностей.
Вышележащие слои могут смещаться по волноводу как по смазке. Это утверждение согласуется с концепцией тектонической расслоенности [Тектоническая расслоенность..., 1980] и основанной на ней идее двухъярусной тектоники плит [Лобковский, 1988]. Согласно этим схемам земная кора состоит из слоев, сильно различающихся по вязкости. Верхняя, наиболее жесткая часть коры, разбита на макроплиты, движущиеся друг относительно друга подобно макроплитам в классической схеме тектоники плит. В рамках последней решается вопрос и о тектонических силах, приводящих в движение всю систему в целом. Это те силы, которые производят внутриплитовые деформации и смещения верхних слоев относительно нижних. Энергия глобального движения переходит в энергию регионального движения микроплит. Эти движения могут быть достаточно сложными и многоуровневыми, поскольку, кроме волновода, пластичными могут быть и самые нижние слои коры, находящиеся в состоянии катакластического течения.
Известно, что проницаемость горных пород достаточно велика (особенно в разломных зонах), а их прочность - мала. Поэтому за геологические масштабы времени флюиды неизбежно отжались бы из волновода, трещины и поры схлопнулись бы, а сами волноводы - исчезли. Простые оценки показывают, что время жизни волноводов в верхней коре порядка 102 -104 лет. Нет никаких оснований считать, что волноводы существуют только в настоящее время. По-видимому они существовали с момента возникновения континентальной коры. Следовательно, должен существовать механизм движения, который периодически засасывает их обратно в волновод и, соответственно, увеличивает трещиноватость последнего.
Сама возможность вязкой реологии отдельных слоев коры подтверждается некоторыми геолого-геофизическими данными. Представления об этих свойствах соответствуют концепции реологической [Николаевский, Шаров, 1985] и тектонической расслоенности [Пейве, 1981], а также концепции двухъярусной тектоники плит [Лобковский, 1988].

|
| Рис. 5 |
Вещество нижнего слоя может находиться в двух состояниях - дилатансии и компакции. В первом случае скелет является упруго-хрупким. Основным фактором, определяющим этот режим, является действующий на микроуровне закон Кулона-Мора, связывающий сдвиговые предельные напряжения t и нормальные напряжения s. При осреднении и переходе на макроуровень этот закон проявляется в виде некоторых соотношений для макровеличин. Поскольку пористая среда волновода насыщенна, то его напряженное состояние определяется принципом Терцаги, в соответствии с которым тензор полных напряжений разделяется на эффективное напряжение sefij и поровое давление p
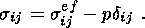 | (1.1) |
Принцип Терцаги гласит, что критерием состояния является тензор эффективных напряжений, точнее говоря, его шаровая часть. Другим независимым параметром состояния является пористость f. Чем больше пористость, тем легче скелет пористой структуры разрушается.
Заметим, что в приближении тонкого слоя вертикальное усилие на подошве упругого слоя постоянно. Оно не зависит от напряженного состояния двухслойной системы (в частности, от дилатансионного расширения в нижнем слое) и равно весу элементарного столба упругого слоя. Поскольку девиаторные напряжения на глубине волновода малы по сравнению с горным давлением, то последнее на кровле волновода постоянно, а с глубиной меняется по закону геостатики. Существенно меняются лишь поровое давление p и шаровая компонента тензора эффективных напряжений sefkk. Эти величины связаны между собой соотношением (1.1). Поэтому из этих двух параметров в качестве независимого управляющего параметра можно взять поровое давление p.
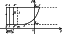
|
| Рис. 6 |
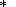 (f), на
которой происходит качественное изменение структуры скелета.
(f), на
которой происходит качественное изменение структуры скелета.
При
pa<s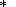 имеет место упругопластический дилатансионный режим. Он
описывается уравнениями дилатансии, которые представляют собой результат
осреднения процесса образования трещин, для каждой из которых выполняется закон
Кулона-Мора. При сдвиговом нагружении в режиме дилатансии происходит
увеличение порового объема, поровое давление падает, и в волновод засасывается
флюид как сверху, так и снизу. Роль дренажных каналов играют разломы. Этот процесс
известен в литературе и многократно описан как сейсмическое или тектоническое
нагнетание или "сейсмический насос''. Увеличение трещинно-порового объема
происходит вплоть до максимального значения пористости
f max, при котором
происходит разрушение скелета пористой среды. В этот момент нагрузка переносится
со скелета на флюид, в результате чего поровое давление резко возрастает.
При
pa>s
имеет место упругопластический дилатансионный режим. Он
описывается уравнениями дилатансии, которые представляют собой результат
осреднения процесса образования трещин, для каждой из которых выполняется закон
Кулона-Мора. При сдвиговом нагружении в режиме дилатансии происходит
увеличение порового объема, поровое давление падает, и в волновод засасывается
флюид как сверху, так и снизу. Роль дренажных каналов играют разломы. Этот процесс
известен в литературе и многократно описан как сейсмическое или тектоническое
нагнетание или "сейсмический насос''. Увеличение трещинно-порового объема
происходит вплоть до максимального значения пористости
f max, при котором
происходит разрушение скелета пористой среды. В этот момент нагрузка переносится
со скелета на флюид, в результате чего поровое давление резко возрастает.
При
pa>s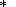 поровое давление настолько велико, что связный скелет
не может существовать в принципе. Он рассыпается на отдельные зерна, которые
могут смещаться друг относительно друга.
поровое давление настолько велико, что связный скелет
не может существовать в принципе. Он рассыпается на отдельные зерна, которые
могут смещаться друг относительно друга.
В этом состоянии вещество волновода превращается в некоторую пористо-зернистую структуру с вязко деформируемым скелетом, который обладает сдвиговой и объемной вязкостями. При этом в процессе деформаций одновременно происходит еще фильтрация флюида. Такая среда описывается уравнениями компакции (иначе - вязкой консолидации).
В режиме компакции дренирование системы очень ограничено (поскольку крупные трещины на выводных каналах и разломах закрываются) и происходит через малопроницаемую кровлю волновода. В процессе компакции пористость уменьшается вплоть до ее минимального значения f = f min, при котором происходит закрытие пор. При этом происходит восстановление скелета из несвязной зернистой структуры и переход из режима компакции в упругопластический режим. Далее цикл повторяется.
Считаем, что в уравнениях компакции сдвиговая вязкость является константой, а объемная вязкость и гидравлическое сопротивление (величина, обратная проницаемости) зависят от пористости. Следовательно, уравнения движения компакции являются, вообще говоря, нелинейными. Однако их решения допускают принцип суперпозиции в отношении сдвиговых и объемных деформаций, т.е. эти составляющие решений можно рассматривать независимо друг от друга. При этом объемные деформации и фильтрационные процессы в нижнем слое можно рассматривать независимо от динамики верхнего слоя. Время фазы компакции равно времени уменьшения пор под действием силы тяжести от максимального до минимального значения. Этот процесс определяет только время фазы компакции (а, следовательно, и весь период волнового движения) и не влияет на режим деформаций двухслойной системы. Взаимодействие нижнего и верхнего слоев в фазе компакции затрагивает только сдвиговые деформации в нижнем слое. Поэтому упругий и вязкий слои образуют единую систему, которая описывается уравнением Эльзассера, аналогично тому, которое описывает двухслойную систему литосфера-астеносфера.
Таким образом, при максимальном f max и минимальном f min значениях пористости происходят изменения структуры порового пространства. Эти состояния циклически сменяют друг друга в квазидинамическом режиме в соответствии с диаграммой на рис. 6. Цикл колебаний соответствует на этой диаграмме замкнутому контуру. В дилатансионной фазе одной и двумя штрихами отмечены участки траектории, соответствующие подошве и кровле волновода. Эти участки являются вертикальными линиями, поскольку изменение порового давления в режиме дилатансии много меньше изменения при компакции. Расстояние между этими линиями равно DrgH1, где Dr - разность плотности скелета и флюида.
Вся система приходит в движение под действием горизонтальной силы тектонического происхождения, приложенной к верхнему упругому слою. Эта сила и является источником энергии всего процесса. В первом приближении верхний слой находится в режиме упругих однородных горизонтальных нормальных напряжений. В следующем порядке малости в этом слое появляются касательные напряжения и градиент нормальных напряжений. Действующие на подошве упругого слоя касательные напряжения уравновешивают нормальные силы в этом слое и создают в нижнем слое сдвиговые деформации. Поэтому волновод всегда находится в условиях сдвиговых деформаций.
Сила сопротивления нижнего слоя верхнему накапливается при увеличении горизонтального размера обоих слоев и стремится к бесконечности при стремлении к бесконечности горизонтального размера этих слоев. Соответственно возрастает до бесконечности и нормальная тектоническая сила, приводящая систему в движение. Тем не менее, уравнения модели допускают волновое решение, которое обладает свойствами периодичности. Возникает необходимость разделить периодическую и непериодическую составляющие и задать такие краевые и дополнительные условия, которые обеспечивали бы корректную постановку задачи.
Основная идея такого разделения состоит в допущении о том, что все нестационарные процессы являются волновыми, а непериодическая составляющая решения является стационарной. Движущей силой процесса являются заданные напряжения на бесконечности, которые описываются статической непериодической составляющей. Эти напряжения и производимая ими работа преобразуются в волновой процесс. Следовательно, необходимо установить связь между этими двумя составляющими через граничные условия.
Заметим, что в такой идеализированной постановке волновой процесс вряд ли возможен в природе. В реальной ситуации следует учитывать третье измерение, а также ограничения размеров во времени и пространстве. Однако возможность корректной постановки задачи и существование идеализированного решения имеют принципиальное значение для понимания физической сущности этого процесса.
После выделения из общего решения для двухслойной системы стационарной монотонно возрастающей составляющей для оставшейся составляющей ищется волновое решение. Оно строится следующим образом. В режиме дилатансии пористость возрастает от минимального до максимального значения. В режиме компакции пористость падает от максимального до минимального значения. Волновая природа решения проявляется в том, что время t входит в виде волнового аргумента (x - ut), где u - скорость волны, которая находится в процессе решения. В действительности же производная по времени входит лишь в уравнения компакции. Поэтому полный период волны определяется временем фазы компакции. Волновое решение можно считать состоявшимся, если удалось построить периодическое решение волнового аргумента. Этот процесс назовем автоволнами. Его движущей силой являются горизонтальные тектонические напряжения. Благодаря особым свойствам указанного вида вещества волновода постоянные горизонтальные тектонические силы вызывают сложные автоволновые процессы двухслойной системы.
Как было сказано выше, в верхнем слое выполняются уравнения теории упругости. На торцевых границах приложены однородные по вертикальному профилю горизонтальные усилия, направленные в положительном направлении оси x. Верхняя граница является свободной, а на подошве действуют касательные напряжения, вызванные взаимодействием с нижним слоем. Предполагаем, что волна движется в отрицательном направлении оси x . В стационарной волне все величины зависят от аргумента y = x + vt. В движущейся системе координат область определения длиной L ограничена вертикальными границами y1<y<y3, L=y3-y1 (рис. 5). Нижний и верхний слои с толщинами H1 и H2 лежат соответственно в интервалах - H1 < z < 0 и 0 < z < H2. Поскольку гидростатическая составляющая решения в верхнем слое в процессе решения не играет никакой роли, вычтем ее из исходных уравнений. Для определенности примем плоско деформированное состояние, при котором поперечные смещения отсутствуют, но поперечные напряжения есть. Имеем
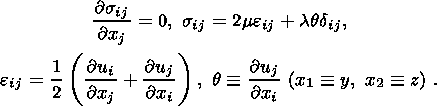 | (2.1) |
Здесь sij и eij - тензоры напряжений и деформаций, q - шаровая часть тензора деформаций, u - вектор смещений, l и m приведенные к плоскому случаю коэффициенты Ламэ, через которые выражается приведенный объемный упругий модуль K=l+m. Таким образом, краевая задача о верхнем слое свелась к задаче о невесомом упругом слое, на границе которого действуют некоторые силы. На верхней границе слоя напряжения отсутствуют, а на его нижней границе напряжения и смещения ui непрерывны. На нижней границе волновода смещения равны нулю
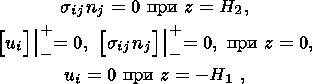 | (2.2) |
где символ [sij]|+- означает скачок величины sij на соответствующей границе, nj - вектор единичной нормали.
Волновой процесс предполагает некоторые условия периодичности, которые полностью выполняются в нижнем слое. В верхнем слое есть волновая и непериодическая статическая составляющие величин. Другими словами, для горизонтальных напряжений sxx и смещений ux справедливо представление
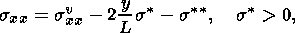 |
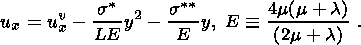 |
Здесь E - аналог модуля Юнга для плоской задачи, svxx и uvx - волновые, составляющие горизонтальных напряжений и смещений, которые удовлетворяют условию периодичности,
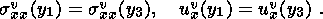 | (2.3) |
Величины
s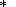 и
s
и
s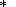
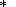 характеризуют усилия на бесконечности,
которые приводят
систему в движение. Точнее говоря
s
характеризуют усилия на бесконечности,
которые приводят
систему в движение. Точнее говоря
s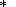 определяет скорость роста напряжений,
а
s
определяет скорость роста напряжений,
а
s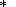
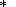 связана с выбором точки отсчета. Знак
минус перед ними соответствует сжимающим
усилиям. Постоянная
s
связана с выбором точки отсчета. Знак
минус перед ними соответствует сжимающим
усилиям. Постоянная
s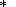
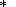 также, как и напряжение
sxx, строго говоря,
стремится к
бесконечности с ростом длины слоев. Однако она может быть вычтена из этих
бесконечных напряжений. Другими словами, вместо
sxx и
ux введем величины
sxx = sxx
+ s
также, как и напряжение
sxx, строго говоря,
стремится к
бесконечности с ростом длины слоев. Однако она может быть вычтена из этих
бесконечных напряжений. Другими словами, вместо
sxx и
ux введем величины
sxx = sxx
+ s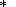
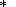 и
ux = ux + 2s
и
ux = ux + 2s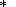
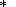 y/LE,
которые уже являются конечными, и за
которыми сохраним прежнее обозначение (т.е. опустим знак тильды), поскольку
бесконечные напряжения и смещения не имеют никакого смысла и нигде ниже не
используются. В результате в краевой задаче в пределах выделенной области
y1 < y < y3 фигурируют только конечные напряжения и
смещения, для которых
справедливо представление
y/LE,
которые уже являются конечными, и за
которыми сохраним прежнее обозначение (т.е. опустим знак тильды), поскольку
бесконечные напряжения и смещения не имеют никакого смысла и нигде ниже не
используются. В результате в краевой задаче в пределах выделенной области
y1 < y < y3 фигурируют только конечные напряжения и
смещения, для которых
справедливо представление
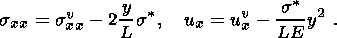 | (2.4) |
Однако при этом следует помнить, что в данном случае величины sxx и ux являются лишь приращениями напряжения и смещения, отсчитываемых от некоторого среднего уровня (который, вообще говоря, является бесконечным). Положим по определению
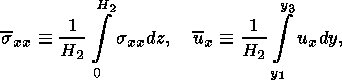 |
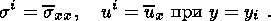 |
Здесь sxx и ux - средние по поперечному профилю значений горизонтальных напряжения и смещения. Величины si и ui определяются в процессе решения. Волновые составляющие по определению удовлетворяют условиям
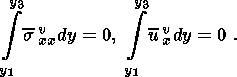 | (2.5) |
Осредняя (2.4) по вертикальному профилю с учетом (2.5), получаем дополнительные соотношения для средних горизонтальных напряжения и смещения
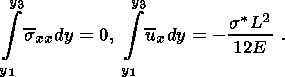 | (2.6) |
В двумерных уравнениях теории упругости (2.1) произведем растяжение вертикальной координаты z = ez
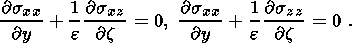 |
Производя разложение величин в этих уравнениях
sij = s(0)ij
+ es(1)ij
+  и т.п., с
помощью несложных рассуждений получаем
и т.п., с
помощью несложных рассуждений получаем
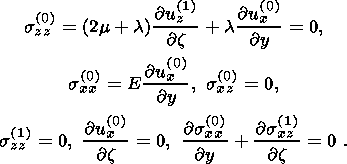 | (2.7) |
Из (2.7) следует, что горизонтальное смещение
u(0)x и нормальное напряжение
s(0)xx
не зависят от поперечной координаты
z: u(0)x u(x), s(0)xx
u(x), s(0)xx s(x). Проинтегрируем
последнее из уравнений (2.7)
по вертикальному профилю с учетом граничных условий (2.2)
s(x). Проинтегрируем
последнее из уравнений (2.7)
по вертикальному профилю с учетом граничных условий (2.2)
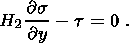 | (2.8) |
Здесь t - касательные напряжения на нижней границе.
Сдвиговые усилия с верхнего слоя передаются в нижний слой и создают в нем движения. Оба возможных состояния, представленных на диаграмме рис. 6, реализуются в двух фазах - дилатансии (в которой происходит разрыхление материала) и компакции (или вязкой консолидации, в которой пористость уменьшается). Для каждой из этих фаз выписаны уравнения движения вместе с соответствующими граничными условиями. Полученные решения "сшиваются'' как с верхним упругим слоем, так и на границе разных фаз. В частности, "сшивание'' смещений и напряжений в верхнем слое на границе фаз приводит к соотношениям
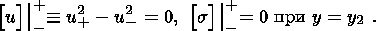 | (2.9) |
Здесь u2+, u2- - значения u на внутренней границе, при приближении к ней соответственно справа и слева.
Подставляя второе выражение (2.7) в первое соотношение (2.6), с учетом (2.9) получаем условие периодичности для приращения смещения (2.3). Следовательно, первое условие (2.6) не является независимым. Производя во втором соотношении (2.6) разложение, получаем
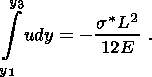 | (2.10) |
Заметим, что уравнение (2.10) содержит параметр
s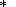 ,
который представляет
собой скорость возрастания статических напряжений на бесконечности. Фактически
это управляющий параметр, описывающий вынуждающее воздействие на систему. Все
остальные величины зависят от этого параметра.
,
который представляет
собой скорость возрастания статических напряжений на бесконечности. Фактически
это управляющий параметр, описывающий вынуждающее воздействие на систему. Все
остальные величины зависят от этого параметра.
Как было показано выше, нижний слой всегда находится в состоянии сдвиговых
деформаций. Смещения в обеих фазах - дилатансии и компакции - отсчитываются от
стационарной составляющей, которая не входит в определяющие уравнения фаз.
Предполагается, что в обеих фазах в сдвиговом режиме нагружения отличными от
нуля являются как сдвиговые, так и шаровые компонентами напряжений и
деформаций. В этих условиях существенной является связь между ними. Она включает
условие Кулона и соотношение между приращениями пластических сдвиговой
gp epxz
и объемной
qp деформаций
epxz
и объемной
qp деформаций
где b - коэффициент дилатансии. Экспериментально явление увеличения объема при сдвиге было обнаружено Рейнольдсом в 1885 г. и названо им дилатансией. Уравнения дилатансии, соответствующие опыту Рейнольдса, в тензорной форме были впервые сформулированы Николаевским [Николаевский, 1967, 1971]. В дальнейшем аналогичные уравнения и их частные случаи были изучены Рудницким и Райсом [Райс, 1982] (которые исследовали проблему бифуркацию решений этих уравнений), а также другими исследователями.
Следуя Райсу [Райс, 1982], введем пластические модули mp, lp, и Kp, аналогичные упругим модулям. Упрощая пластическую картину деформирования, ограничимся сдвиговыми деформациями
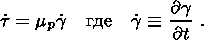 | (3.1) |
Пластические модули зависят от условий дренирования. Первое допущение требует, чтобы при любых динамических процессах изменение порового объема было мало по сравнению со средним значением этого объема. Поэтому предполагаемые условия дренирования в дилатансионном режиме сказываются лишь на флюидном режиме верхнего слоя и не влияют на режим пластических деформаций в самом волноводе. Это означает, что в соотношении (3.1) следует иметь в виду недренажный модуль сдвиговых деформаций при любых деформациях - нагрузки или разгрузки. Другое допущение состоит в том, что пренебрегаем упругой составляющей деформаций. Тогда полная деформация совпадает с пластической составляющей, а дилатансионное изменение объема обусловлено только изменением пористости dq = df
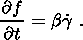 | (3.2) |
Третье допущение вытекает из первых двух и предполагает малость величины пластических модулей mp, lp и Kp по сравнению с их упругими аналогами m, l и K. Физический смысл всех этих допущений сводится к предположению о том, что трещиноватая среда в нижнем слое находится в субкритическом состоянии. По этой причине малы пластические модули, малы изменения пористости и очень велики сдвиговые пластические деформации.
Четвертое допущение касается структуры слоев. Считаем, что на кровле волновода находится малопроницаемая покрышка, которая обеспечивает условие слабого дренирования волновода. Именно благодаря этой покрышке в критической точке разрушения скелета среды при изменении состояния среды вес вышележащего упругого слоя переносится со скелета среды на поровое давление, что требуется для режима вязкой консолидации в среде с разрушенным скелетом. При отсутствии указанной покрышки фаза разгрузки в волноводе будет проходить в условиях упругого деформирования. Скорее всего такие условия реализуются на кристаллических щитах подобных Канадскому и Фенноскандинавскому. Там нет пластичных осадочных пород, которые могли бы создать непроницаемую покрышку для волновода. Поэтому там колебательный процесс в волноводе может происходить только без фазы компакции. Подставляя (3.1) в (3.2), получаем
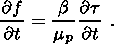 | (3.3) |
Будем отсчитывать деформацию в нижнем слое от состояния с минимальной пористостью, в котором деформация равна нулю. Горизонтальное смещение на кровле волновода u равно горизонтальному смещению верхнего упругого слоя, которое однородно по вертикальному профилю этого слоя. В каждой из фаз это горизонтально смещение будем отсчитывать от начальной точки, с которой начинается развитие данной фазы. В фазе дилатансии начальная точка равна y1, а начальное смещение - u1. В фазе компакции эти величины обозначаются соответственно как y2 и u2. Между эти величинами есть очевидное кинематическое соотношение u-u1=H1g. С учетом его уравнения (3.2) и (3.3) элементарно интегрируются
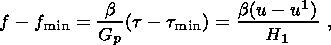 | (3.4) |
т.е. с ростом сдвиговых деформаций в зоне волновода пористость f и сдвиговое напряжение t возрастают от своих минимальных уровней f min и t min до критических значений f max и t max, при котором происходит разрушение скелета и переход в вязкую фазу в полном соответствии с критерием, представленным на диаграмме рис. 6 и основанном на принципе Терцаги. Если критические значения пористости f min и f max известны и определяются с помощью диаграммы на рис. 6, то t min и t max являются величинами, которые находятся в процессе решения. Из (3.4) следует соотношение
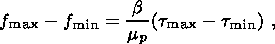 | (3.5) |
которое связывает t max и t min.
В силу сказанного на границах зон дилатансии и компакции имеем соотношения
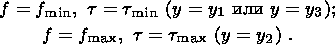 | (3.6) |
Значение пористости f = f max является начальным значением этой величины для фазы компакции. Сдвиговая деформация в нижнем слое связана со смещением верхней границы этого слоя кинематическим соотношением
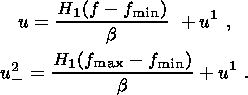 | (3.7) |
Здесь
u2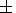 - значение величины
u2 при приближении к границе раздела фаз
соответственно справа и слева.
- значение величины
u2 при приближении к границе раздела фаз
соответственно справа и слева.
Комбинируя второе соотношение (2.7), (2.8) и (3.4), приходим к уравнению
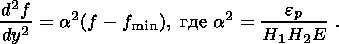 | (3.8) |
Решая уравнение (3.8) при условии (3.6), получаем
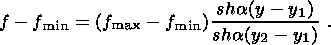 | (3.9) |
Заметим, что
a (y2 - y1)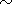 1. Поскольку
E
1. Поскольку
E mp,
то длина фазы дилатансии
(y2 - y1) много больше, чем толщины слоев
H1 и
H2. С помощью (3.9), (3.7) и
второго соотношения (2.7) можно определить выражения для смещения и напряжений
mp,
то длина фазы дилатансии
(y2 - y1) много больше, чем толщины слоев
H1 и
H2. С помощью (3.9), (3.7) и
второго соотношения (2.7) можно определить выражения для смещения и напряжений
 | (3.10) |
Эти выражения позволяют получить граничные значения величин
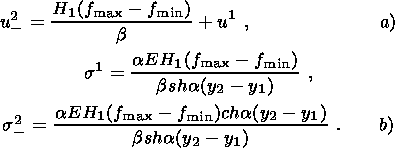 | (3.11) |
Выражение (3.11) связывает длину фазы дилатансии с амплитудой напряжений в начальной точке волны.
Уравнения компакции согласно [Каракин, 1990b, 1999] допускают принцип суперпозиции, в силу которого сдвиговые и объемные деформации можно рассматривать независимо друг от друга. Рассмотрим вначале сдвиговые движения в зоне компакции, которые можно состыковать со сдвиговыми движениями в зоне дилатансии. В зоне компакции все расчеты, выполненные в упругом слое, сохраняют свою силу. Различие наступает лишь в нижнем слое, в котором имеют место вязкие деформации. В частности, вместо (3.3) имеем аналогичное уравнение для вязких деформаций в нижнем слое
Комбинируя последнее уравнение с (2.8), а также со вторым уравнением (2.7), получаем известное параболическое уравнение в двухслойной системе, выведенное Эльзассером [Elsasser, 1971],
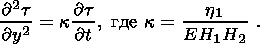 |
Переходя в этих двух соотношениях к волновому аргументу, получаем уравнения
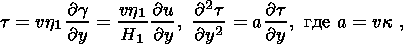 | (4.1) |
последнее из которых легко решается с учетом граничного условия (3.6)
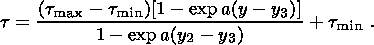 | (4.2) |
Как и следовало ожидать, в зоне компакции касательное напряжение меняется от своего максимального до минимального значения. Из (2.8), (4.1) и (4.2) следуют выражения для нормального напряжения и его граничного значения на внутренней границе
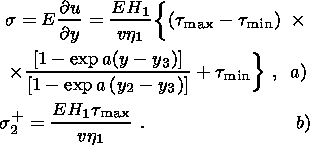 | (4.3) |
Проинтегрируем выражение (4.3a) с учетом условия периодичности смещений (2.12)
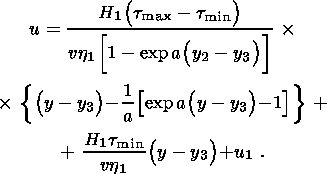 | (4.4) |
Условие (2.9) непрерывности смещения на внутренней границе с учетом (4.4) и (3.7) приводит к
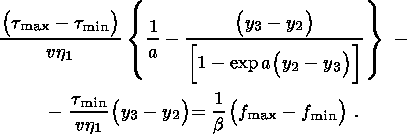 | (4.5) |
Аналогичное соотношение вытекает из условия непрерывности нормальных напряжений (2.9) с учетом (3.10), (4.3b)
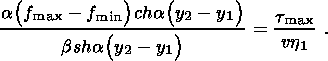 | (4.6) |
Из (4.6) следует, что v>0, т.е. волна действительно (как это и было предположено) бежит в направлении, обратном направлению действия тектонической силы. Исключая в (3.5), (4.5) и (4.6) неопределенные величины t min и t max, получаем соотношение, связывающее длины фаз компакции и дилатансии,
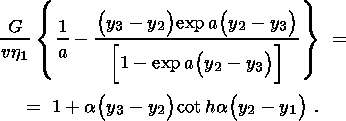 | (4.7) |
Условие периодичности нормальных напряжения приводит к соотношению
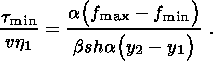 | (4.8) |
Подставляя (4.4) и (3.10a) в (2.10), получаем выражение для определения u1
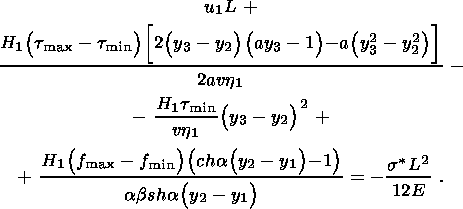 | (4.9) |
Пусть Tc - время компакции, которое определяется ниже в результате решения краевой задачи компакции. Оно связано со скоростью движения волны соотношением
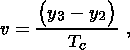 | (4.10) |
которое позволяет определить длину фазы компакции (y3 - y2). Решая шесть уравнений (3.5), (4.5), (4.6), (4.8) (4.9) и (4.10), можно найти шесть искомых величин u1, t min t max, (y2 - y1), (y3 - y2) и v, выраженные через Tc. Тем самым окончательное решение задачи сводится к определению времени компакции Tc, которое находится в результате решения одномерной задачи компакции.
В этой связи рассматривается одномерная задача компакции в конечной области
-H1
Здесь
S - фильтрационный поток,
f - пористость,
d - коэффициент
гидравлического сопротивления,
z и
h - коэффициенты объемной и сдвиговой
вязкости. Толщина слоя является переменной и зависит от горизонтальной координаты
x как от параметра. Нижняя граница
G1 зоны вязкой консолидации в зависимости
от значения пористости
на ней может быть подвижной или неподвижной. В нестационарной ситуации на ней
возможны различные режимы движения. В частности, при
f>f min она неподвижна, и
на ней справедливо условие
Когда пористость на этой границе достигает значения
f min, граница начинает
двигаться вверх вплоть до соприкосновения с верхней границей
G2. В случае движения
стационарной волны возможна только такая ситуация, при которой на нижней границе
имеем условие отступающего фронта
Верхняя граница волновода
G2 является неподвижной. Выше этой
границы
находится пористый слой с упругим скелетом. В этом слое необходимо решать
краевую задачу пьезопроводности (задачу упругой консолидации) и полученное
решение "сшивать'' с решением в волноводе. Однако для целей качественного
исследования условие сшивания можно заменить более простым условием
где
p
Для каждого цикла колебаний начальный момент времени совмещаем с началом
фазы компакции. Поскольку уравнения для сдвиговых и объемных деформаций
расщепляются, то время в каждую из этих групп уравнений входит независимо.
Краевая задача (4.11)-(4.15) решалась численно. Процедура и результаты расчета
приведены в работе
[Каракин, Левитан, 1993].
Оказывается, что время, за которое область компакции уменьшается до нуля, является
конечным. Это время и есть период фазы компакции
Tc. Тем самым задача решена полностью.
Граничное условие (4.14) определяет масштаб перепада давления в волноводе.
Он больше или порядка
DfK, где
Df - полное изменение пористости в течение
одного цикла колебаний в волноводе,
K - упругий объемный модуль верхнего слоя.
Поскольку дилатансионный объемный модуль
Kp много меньше
K, то
соответственно изменение порового давления в дилатансионной фазе много меньше
изменения порового давления в фазе компакции. По этой причине траектории на
диаграмме рис. 6
в фазе дилатансии, а также линия раздела фаз представляют собой
вертикальные линии.
Таким образом, если к изучаемой двухслойной системе приложить силу, то
возможен автоволновой режим движения этой системы. Этот режим обусловлен
периодическими процессами отжимания флюидов из волновода и их засасывания в
волноводный слой. Фаза компакции намного продолжительнее фазы дилатансионного
расширения. Взаимодействие указанных режимов поддерживает в волноводе
состояние динамического равновесия.
Как известно, в теории органического происхождения нефти есть
принципиальные трудности. Согласно этой теории углеводороды при
соответствующих термодинамических условиях образуются из органического
вещества, равномерно рассеянного по всему осадочному покрову. При этом
рассеянные углеводороды концентрируются в месторождениях, занимающих
относительно небольшие объемы. Этот факт имеет парадоксальный характер. На
первый взгляд он противоречит термодинамике, согласно которой все находящиеся в
дисперсной форме вещества имеют тенденцию рассеиваться, а не собираться вместе.
Возникает проблема, каким образом объяснить этот парадокс. Эта проблема, хотя и в
не столь явной форме, существует и в теории неорганического происхождения нефти.
Если все углеводороды имеют эндогенное происхождение, то поднимаясь вверх, они
также как и в первом случае должны равномерно рассеиваться по всей коре.
Другой парадокс состоит в том, что и у сторонников органического, и у
сторонников неорганического происхождения углеводородов есть достаточно
убедительные доводы в пользу своей точки зрения. Возникает некий дуализм - вроде
как бы обе точки зрения в равной степени приемлемы, и не существует объективного
критерия для выбора между ними.
Эти противоречия и парадоксы можно разрешить, если предположить: флюиды в
земной коре совершают сложные колебательные движения и многократно проходят
одни и те же пути как по горизонтали, так и по вертикали. В этом случае не имеет
принципиального значения вопрос о происхождении углеводородов, а механизм
концентрации углеводородов также не зависит от их генезиса.
Предложенная концепция объясняет многие факты. В частности, факт
расположения грязевых вулканов в быстро опускающихся осадочных бассейнах на
антиклинальных сводах рассеченных разломами. Потоки флюидов, прорывающиеся
сквозь антиклинальные своды ловушек, могут содержать углеводороды и грязе-вулканическую
брекчию. Они формируют каналы грязевых вулканов, которые
обладают слабой сейсмической контрастностью.
На основе данной концепции были проведены численные расчеты движения
двухфазной газожидкостной смеси в верхней коре в Варандей-Адзвинской
нефтегазоносной провинции
[Dmitrievski et al., 2000].
Был промоделирован, в частности, процесс образования газовых месторождений
в этом регионе. Численными методами были исследованы процессы движения
газожидкостной смеси из корового волновода в вышележащие слои и образования
газовых месторождений.
При этом возможно образование УВ месторождений типа Сахалинских
шельфовых месторождений. Как и в случае континентальных месторождений, если
ловушки нарушены разломами, то вместо месторождений углеводородов образуются
грязевые вулканы (рис. 9). Однако, в обличие от континентальных вулканов, в зонах
субдукции в районе глубоководных впадин вместо песчано-глинистой грязевой смеси
извергается разжиженный серпентинит.
Ботт М. Н. П., Внутреннее строение Земли, Мир, Москва, 1974.
Пер с англ.: Bott M. N. P., The interior of the Earth, London: Edward
Arnold. 1971.
Ваньян Л. Л., Электропроводность земной коры в связи с ее флюидным режимом, Коровые
аномалии электропроводности, с. 27-34, Наука, Л., 1984.
Ваньян Л. Л., Шиловский П. П., Глубинная электропроводность океанов и континентов,
86 с., Наука, Москва, 1983.
Гордин В. А., Каракин А. В., Солитонные решения задач вязкой консолидации,
Математическое моделирование, 2, (2), 98-116, 1990.
Григорьев С. М., Роль воды в образовании земной коры (дренажная оболочка земной
коры), 261 с., Недра, Москва, 1971.
Каракин А. В., Модель движения флюидов в земной коре за геологические отрезки
времени, Математическое моделирование, 2, (93), 31-42, 1990a.
Каракин А. В., Модели флюидодинамики земной коры с неупругим скелетом,
Изв. АН СССР, Физика Земли, (2), 3-15, 1990b.
Каракин А. В., Лобковский Л. И., Механика пористой двухфазной астеносферы,
Изв. АН СССР, МЖГ, (6), 53-63, 1979.
Каракин А. В., Левитан С. Ю., Моделирование флюидодинамических процессов в
горных породах с вязким скелетом, В сб.: Математическое моделирование геологических
процессов, с. 17-32, ВНИИГеосистем, Москва, 1993.
Каракин А. В., Общая теория компакции при малой пористости, Физика Земли,
(12), 13-26, 1999.
Каракин А. В., Камбарова Г. Н., Динамическая модель коровых волноводов,
Геоинформатика, (4), 10-17, 1997.
Кольская сверхглубокая скважина, 490 с., Недра, Москва, 1984.
Краснопевцева Г. В., Геолого-геофизические особенности строения слоев с
пониженными скоростями в земной коре, Региональная, разведочная и промысловая
геофизика, Обзор, 40 с., ВИЭМС, Москва, 1978.
Лобковский Л. И., Геодинамика зон спрединга, субдукции и двухъярусная тектоника
плит, 252 с., Наука, Москва, 1988.
Магницкий В. А., Слой низких скоростей верхней мантии Земли, 292 с.,
Наука, Москва, 1968.
Николаевский В. Н., О связи объемных и сдвиговых пластических деформаций и
об ударных волнах в мягких грунтах, ДАН СССР, 177, (3), 542-545, 1967.
Николаевский В. Н., Определяющие уравнения пластического деформирования
сыпучей среды, ПММ, 36, вып. 6, 1017-1029, 1971.
Николаевский В. Н., Шаров В. И., Разломы и реологическая расслоенность земной
коры, Изв. АН СССР, Физика Земли, (1), 16-27, 1985.
Райс Дж., Механика очага землетрясений, 214 с., Мир, Москва, 1982.
Перевод Rice J. R., Mechanics of Earthquake Rupture, in: Phisics of
the Earth's Inerior., Proceedingsof the International School of Physics "Enrico
Fermi'' Course 78, 1979, edited by Dziewonski and Boschi, Italian Physical
Society, 1980. Amsterdam, North-Holland, 1980.
Пейве А. В., Мобилизм и тектоническая расслоенность литосферы,
Природа, (2), 2-9, 1981.
Сейсмические модели литосферы основных геоструктур территории СССР, Сборник,
184 с., Наука, Москва, 1980.
Смит Ф. Г., Физическая геохимия, 178 с., Недра, Москва, 1968.
Тектоническая расслоенность литосферы, 216 с., Наука, Москва, 1980.
Теркот Д., Шуберт Дж., Геодинамика, Геологические приложения физики сплошных
сред, ч. I, II, 730 с., Мир, Москва, 1985. Пер с англ.
D. L. Turcotte, G. Schubert, Geodynamics, Applications of Continuum
Physics
to Geological Problems, John Wiley & Sons, 1982.
Файф У., Прайс Н., Томпсон А., Флюиды в земной коре, 436 с., Мир, Москва,
1981 (Перевод с английского).
Fyfe, W. S., N. J. Price, and A. B. Thomson, Fluids in the Earth's
crust,
Elseveir Scientific Publishing Company Amsterdam, 1978.
Barcilon, V., O. Lovera, Solitary waves in magma dynamics, J. Fluid Mech., 204,
121-133, 1989.
Dmitrievski, A. N., I. E. Balanyuk,
Yu. A. Poveshchenko, A. V. Karakin,
M. I. Lodzhevskaya, Mechanism for hydrocarbon deposit emergence, Gas
Indusdtry of Russia, p. 5-9, Digest 2000.
Gutenberg, B., Physics of the Earth's Interiors, New-York, Academic Press,
1959.
Elsasser, W. H., Two-layer model of upper mantle circulation, J. Geophys. Res.,
76, 1101-1112, 1971.
Feldman, I. S., On the nature of conductive layers in the Earth's crust and upper
mantle,
Geoelec. and Geotherm. Stud. KAPG Geophys. Monogr. Bp., 721-745, 1976.
McKenzie, D., The generation and compaction of partially molten rock,
Journal of Petrology, 25, (3), 713-765, 1984.
Nikolaevskii, V. N., Mechanics of Porous and Fractured Media, pp. 472,
Singapore: World Scientific, 1990.
Ranalli, G., and D. C. Murphy, Rheological stratification of the lithosphere,
Tectonophysics, 132, (4,), 281-295, 1987.
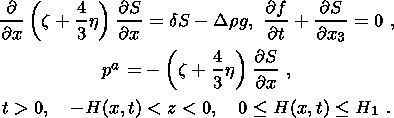
(4.11) 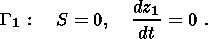
(4.12) 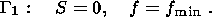
(4.13) 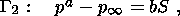
(4.14) 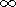 - значение
порового давления в верхнем слое далеко от границы ("на
бесконечности''). Смысл этого условия заключается в следующем. Характерное время
упругой консолидации (которое оценивается, исходя из уравнения пьезопроводности)
много меньше времени вязкой консолидации. Поэтому это условие не содержит
производной по времени и аналогично соотношению теплопередачи для уравнения
теплопроводности. Константа
b выражается через геометрические и фильтрационные
характеристики области с упругим скелетом, расположенной над волноводом. При
p
- значение
порового давления в верхнем слое далеко от границы ("на
бесконечности''). Смысл этого условия заключается в следующем. Характерное время
упругой консолидации (которое оценивается, исходя из уравнения пьезопроводности)
много меньше времени вязкой консолидации. Поэтому это условие не содержит
производной по времени и аналогично соотношению теплопередачи для уравнения
теплопроводности. Константа
b выражается через геометрические и фильтрационные
характеристики области с упругим скелетом, расположенной над волноводом. При
p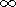 направление
фильтрационного потока меняет знак, поэтому в этой точке он
обращается в нуль. Следовательно, условие (4.14), хотя и грубо, но приблизительно
правильно передает основные черты взаимодействия двух сред на границе
G2.
В систему краевых условий входит также начальное условие для
пористости. Как уже говорилось, начальное условие определяется пористостью,
которая имеет место в момент перехода от режима дилатансии к режиму компакции.
Следовательно, начальное условие имеет вид
направление
фильтрационного потока меняет знак, поэтому в этой точке он
обращается в нуль. Следовательно, условие (4.14), хотя и грубо, но приблизительно
правильно передает основные черты взаимодействия двух сред на границе
G2.
В систему краевых условий входит также начальное условие для
пористости. Как уже говорилось, начальное условие определяется пористостью,
которая имеет место в момент перехода от режима дилатансии к режиму компакции.
Следовательно, начальное условие имеет вид
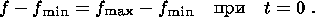
(4.15) 5. Заключение. Вертикальная миграция флюидов в верхней
коре
Cхематически действие автоволнового механизма движения флюидов
в
волноводе и вышележащих слоях показано на рис. 7. В режиме дилатансии
нисходящие потоки флюидов закачиваются в волновод по листрическим разломам,
которые своими корнями входят в него. В процессе нисходящих движений водные
флюиды увлекают углеводороды в зону волноводов. Растворимость углеводородов в
воде ничтожна (менее 1%). Поэтому в верхних слоях коры, где пористость в
листрических разломах достаточно велика, они переносятся в виде эмульсии. На
глубинах, соответствующих волноводу, термодинамические условия таковы, что их
растворимость (особенно газовой фазы) увеличивается. Это создает предпосылки для
накопления и концентрации углеводородов в зоне волновода. Хотя за единичный
волновой цикл относительная доля углеводородов относительно невелика, их масса
(увлеченная в волноводы) за геологические масштабы времени и на достаточно
больших площадях оказывается весьма существенной.

Рис. 7
На протяжении фазы компакции флюиды из волновода отжимаются
вверх. По
мере продвижения флюиды могут упираться в непроницаемые антиклинальные
структуры (ловушки) и генерировать аномально высокие давления (АВПД). Обычно
ловушки образованы антиклинальными складками непроницаемых пород. Если в
восходящие потоки флюидов попадают концентрированные углеводороды, то
возникают условия для образования их месторождений. В тех случаях, когда свод
антиклинальных структур рассечен сетью разрывных нарушений (рис. 8), то по этим
разломным зонам флюиды устремляются вверх и выбрасываются на дневную
поверхность, образуя газовые выбросы или грязевые вулканы. Согласно предложенной
гипотезе реально существующие нефтегазоносные поля и грязевые вулканы имеют
общую природу. Единственное отличие грязевых вулканов состоит в том, что у них
ловушки нарушены. Это объясняет расположение грязевых вулканов вдоль разломов и
на склоне шельфа во флексурной зоне, где непроницаемые слои больше всего
подвергаются разрушению.
Рис. 8
Особенность геологического строения и геодинамического развития
этой зоны
состоит в том, что она является бывшей зоной субдукции, образовавшейся при
схлопывании древнего океана. В процессе коллизии литосферных плит были затянуты
в недра огромные массы осадочных пород пассивных окраин. Эти массы содержали
большое количество органического вещества и в настоящее время являются
нефтематеринскими породами. Они имеют большой потенциал образования
углеводородных месторождений. Однако необходим движущий механизм, который
реализовывал бы этот потенциал. Таким механизмом являются автоволновые
движения в коровом волноводе. На рис. 9 схематически показан процесс затягивания
вещества пассивных окраин в зоне субдукции. Волновод расположен в
континентальной коре и пересекает субдуцируемую литосферную плиту в
горизонтальном направлении. Действие волновода аналогично его действию в
континентальной области.

Рис. 9
Когда процесс субдукции заканчивается, в этом месте через
некоторое время
образуется структура зоны эксколлизии типа Варандей-Адзвинской нефтегазоносной
провинции (рис. 10).
Отличительной чертой зон субдукции и особенно зон
эксколлизии является типичная дифференцированность этих зон в крест простирания,
показанная на рис. 10. На фронтальной части зоны, соответствующей уходящей вглубь
плите, располагаются газовые месторождения. В тыловой части находятся и тяжелые
нефти и битумы. В средней части расположены нефти промежуточного состава. Эта
дифференциация углеводородных месторождений по их составу полностью
соответствует особенностям действия механизма движения флюидов в коровом
волноводе. Во фронтальной части флюиды поступают в волновод снизу при высоких
температурах и давлениях. Это способствует выделению из нефтематеринских пород
газовой фракции в большом количестве. В тыловой части идет промывка
нефтематеринских пород, расположенных над волноводом, при низких температурах и
давлениях. При этом, естественно, образуются тяжелые нефти и битумы.

Рис. 10
Литература
Загрузка файлов для печати и локального просмотра.
This document was generated by TeXWeb
(Win32, v.1.3) on November 4, 2000.
