Ю. И. Галушкин, Е. П. Дубинин, А. А. Свешников, С. А. Ушаков
Московский государственный университет им. М. В. Ломоносова, Музей землеведения
Термические модели океанической литосферы, интенсивно развивавшиеся в последние 30-35 лет, условно можно разделить на 2 основные группы. В первую входит относительно небольшое число пионерских работ, объяснявших природу генеральных черт рельефа дна океана и теплового потока литосферы СОХ [Сорохтин, 1973; McKenzie, 1967; Oldenburg, 1975; Parker and Oldenburg, 1973; Schubert et al., 1975], а во вторую - работы, анализирующие механизмы генерации океанической коры в осевых зонах СОХ и особенности формирования рельефа и теплового потока этих зон. Вторую более многочисленную группу работ можно разделить, в свою очередь, на 4 подгруппы по характеру решаемых проблем и способам их решения. Анализ проблем в первых трех этих подгруппах проводится на основе стационарных моделей теплообмена и массопереноса, и только последняя, четвертая подгруппа рассматривает нестационарные модели формирования коры и характерных структур приосевой области хребта.
Первая из упомянутых подгрупп включает в себя стационарные тепловые модели с горизонтальным движением коры и аналитическим полем скоростей расходящегося течения невязкой мантии в литосфере. Модели анализируют соотношения толщины литосферы и корового слоя при разных скоростях спрединга и заметной роли гидротермальной деятельности [Chen and Morgan, 1990; Eberle and Forsyth, 1998; Neumann and Forsyth, 1993; Phipps Morgan et al., 1987]. Модели второй подгруппы рассматривают стационарный теплообмен со стационарным полем скоростей миграции расплава и деформации коры и мантии при переменной вязкости среды. Их цель - объяснить изменение мощности коры в зависимости от скорости спрединга, характера сегментации хребта и положения изучаемого участка осевой зоны хребта относительно краев сегмента [Barnouin-Jha et al., 1994, 1997; Chen and Phipps Morgan, 1996; Cordery and Phipps Morgan, 1992, 1993; Phipps Morgan and Chen, 1993; Sotin and Parmentier, 1989; Sparks and Parmentier, 1991, 1993; Sparks et al., 1993; Spiegelman and McKenzie, 1987]. Третью подгруппу моделей составляют все стационарные тепловые модели, анализирующие проблемы существования подосевых коровых очагов магмы [Chen and Phipps Morgan, 1996; Henstock et al., 1993; Morton and Sleep, 1985; Phipps Morgan and Chen, 1993; Sleep, 1975; Sleep et al., 1983; Wilson et al., 1988]. И, наконец, в четвертой подгруппе рассматривается нестационарная тепловая модель подосевых коровых очагов магмы, позволяющая анализировать процесс формирования корового очага от момента его зарождения до становления его устойчивой формы, а также проследить процесс его деградации после прекращения спрединга [Галушкин, Дубинин, 1993; Галушкин и др., 1994а, 1994б].
Первая термическая модель, объяснявшая природу генерального рельефа и теплового потока СОХ, была предложена Д. МакКензи [McKenzie, 1967]. В ней распределение температур, тепловой поток и рельеф поверхности океанической литосферы определялись решением стационарного уравнения теплопроводности для литосферной плиты постоянной толщины, движущейся с постоянной скоростью V от оси хребта ( V - полускорость спрединга):
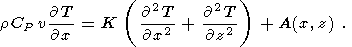 | (1) |
где
K - коэффициент теплопроводности,
r - плотность и
СP - теплоемкость пород
литосферы;
v - скорость спрединга;
T(x,z) - температура пород и свободный член
уравнения
A(x,z) = 0. Граничные условия имели вид:
T=T0=0 при
z=0 ;
T=T1 на нижней границе литосферы
z=H ;
T=T1 на оси
x=0 и
 T/
T/ x
x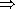 0 при
x
0 при
x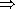
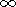 .
Решение искалось в виде ряда Фурье и имело вид
[McKenzie, 1967]:
.
Решение искалось в виде ряда Фурье и имело вид
[McKenzie, 1967]:
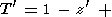 | (2) |
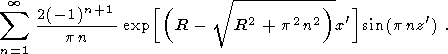 |
Здесь
T=(T1-T0)T +T0,
x=Hx
+T0,
x=Hx ,
z=Hz
,
z=Hz и
R=rCP vH/2k - число Релея. В области
x, где
толщина литосферы заметно отличается от асимптотической, решение (2) близко к
известному решению для остывающего полупространства с начальной температурой
T=Ts=T1 [Карслоу, Егер,
1964]:
и
R=rCP vH/2k - число Релея. В области
x, где
толщина литосферы заметно отличается от асимптотической, решение (2) близко к
известному решению для остывающего полупространства с начальной температурой
T=Ts=T1 [Карслоу, Егер,
1964]:
| 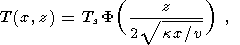 | (3) |
где F - функция вероятности и k=K/rCP - термическая диффузия пород. Модель остывающего полупространства (3) была использована в 1972 г. О. Г. Сорохтиным, в нашей стране, и Р. Паркером и Д. Олденбургом, за рубежом, чтобы получить известные законы изменения теплового потока:
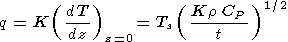 | (4) |
и рельефа хребта, h, как 1/(t1/2) и аналогичной зависимости для мощности океанической литосферы: TL/TS = F(HL/(2(kx/v)1/2)), которая определяется из (1) по соотношению T=TL и предполагает рост толщины литосферы пропорционально t1/2 (рис. 1) [Сорохтин, 1973; Parker and Oldenburg, 1973]. Здесь TL - температура, близкая к температуре солидуса материала мантии литосферы и t=x/v - возраст литосферы.
Модификацию решения Д. МакКензи для учета эффекта выделения скрытой
теплоты плавления предпринял Д. Олденбург в моделях 1973 и 1975 гг. Он
искал
распределение температур в океанической литосфере в рамках решения типичной задачи
Стефана, задавая на нижней переменной границе литосферы температуру, равную
температуре солидуса:
z=HL(x) при
T=TL и определяя на этой границе скачок теплового
потока, обусловленный выделением скрытой теплоты плавления материала мантии:
K(nx T/
T/ x + nz
x + nz T/
T/ z) = -Lrv. Чтобы
избежать особенности в решении на оси хребта, вводилось дополнительное условие
при
x =0 и
0
z) = -Lrv. Чтобы
избежать особенности в решении на оси хребта, вводилось дополнительное условие
при
x =0 и
0 z
z 1: -K(
1: -K( T/
T/ x)=rv[L+CP(TL-Tf)],
которое предполагало, что все тепло, приносимое интрузиями в осевую зону, уносится
горизонтальным тепловым потоком. Выше l - значения толщины литосферы на оси,
предполагаемое заранее,
Tf - эффективная температура интрузий,
nx и
nz - компоненты вектора внешней нормали к нижней границе
литосферы
HL(x).
Задача решается численно, но из характера решения следует, что глубины изотерм,
рельеф, тепловой поток и мощность литосферы остаются функциями
t1/2 и в
этой модели решения. С удалением от оси, в области
x
x)=rv[L+CP(TL-Tf)],
которое предполагало, что все тепло, приносимое интрузиями в осевую зону, уносится
горизонтальным тепловым потоком. Выше l - значения толщины литосферы на оси,
предполагаемое заранее,
Tf - эффективная температура интрузий,
nx и
nz - компоненты вектора внешней нормали к нижней границе
литосферы
HL(x).
Задача решается численно, но из характера решения следует, что глубины изотерм,
рельеф, тепловой поток и мощность литосферы остаются функциями
t1/2 и в
этой модели решения. С удалением от оси, в области
x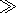 2lK/rvCP,
где
2lK/rvCP,
где
 2T/
2T/
 x2
x2 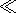 (rCP
v/K)(
(rCP
v/K)( T)/(
T)/( x), получается
асимптотическое решение, которое полностью аналогично (3).
x), получается
асимптотическое решение, которое полностью аналогично (3).
Согласно асимптотическому решению, толщина литосферы продолжала
неограниченно расти как
t и для большого возраста океанической литосферы. Однако,
наблюдения показывают, что при возрасте коры
t>70 млн лет глубины изотерм и
поверхности дна океана, а также тепловой поток, крайне медленно меняются с возрастом
[Parson and Sclater, 1977],
качественно согласуясь с моделью остывающей плиты
McKenzie [1967].
Дж. Шуберт с соавторами
[Schubert et al., 1975]
пытался исправить это положение, рассматривая зависимость коэффициента
теплопроводности от температуры и эффект выделения тепла вязкого трения в
основании литосферы, вызванного скольжением последней в верхних слоях вязкой
астеносферы. Авторы установили, что если теплопроводность пород мантии зависит
только от температуры, как, например, в работе
[Schatz and Simmons, 1972],
то глубины изотерм, тепловой поток и рельеф поверхности литосферы будут
по-прежнему изменяться как функции
t1/2. Расчеты со
значениями геофизических параметров, типичных для пород мантии литосферы и
астеносферы, показали, что тепло вязкого трения слабо сказывается на тепловом режиме
литосферы для полускоростей спрединга
V<5 см/год, в то время как для
V=10 см/год заметное отклонение от закона
t1/2 наблюдалось уже для возраста
литосферы
t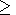 25 млн лет, что также противоречит наблюдениям.
Тогда, чтобы
снять противоречие, Д. Ольденбург
[Oldenburg, 1975]
предположил, что характер конвективных движений в
астеносфере и глубокой мантии определяет некоторую постоянную величину глубинного
теплового потока из мантии с удалением от оси спрединга, тем самым устанавливая
асимптотический тепловой режим литосферы аналогично тому, как это имеет место и в
модели плиты постоянной толщины.
25 млн лет, что также противоречит наблюдениям.
Тогда, чтобы
снять противоречие, Д. Ольденбург
[Oldenburg, 1975]
предположил, что характер конвективных движений в
астеносфере и глубокой мантии определяет некоторую постоянную величину глубинного
теплового потока из мантии с удалением от оси спрединга, тем самым устанавливая
асимптотический тепловой режим литосферы аналогично тому, как это имеет место и в
модели плиты постоянной толщины.
Хотя в целом рассмотренные модели неплохо описывали генеральные черты изменения теплового потока, рельефа дна и мощности океанической литосферы с возрастом, однако продолжающиеся геофизические исследования приносили новую информацию о строении и геофизических полях литосферы срединно-океанических хребтов, и особенно их осевых зон. Открывшееся своеобразие теплового потока, рельефа осевых долин и поднятий, особенности гравитационных и магнитных полей в осевых зонах хребта требовали уточнения существующих тепловых моделей.
Н. Слип [Sleep, 1974, 1975]
первым анализировал распределение теплового потока
и температур в осевой зоне СОХ. Он решал стационарное уравнение теплопроводности
(1) c
A(x,z)=0 в прямоугольной области
x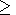 0, 0
0, 0 z
z H со стандартными
граничными условиями:
T=0 на поверхности области счета
(z=0), T=TH в ее
основании
(z=H) и
H со стандартными
граничными условиями:
T=0 на поверхности области счета
(z=0), T=TH в ее
основании
(z=H) и
 T/
T/ x=0 при
x=
x=0 при
x=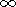 . На оси
x=0 задавался тепловой поток:
. На оси
x=0 задавался тепловой поток:
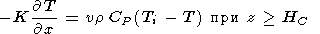 | (5) |
где HC - толщина коры, и
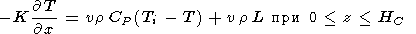 | (6) |
в пределах коры. Здесь
L = 90 кал/г - скрытая теплота плавления базальта. Температура
пород интрузивной зоны
Ti росла с глубиной по кусочно-линейному закону с
градиентом
dTi/dz=3 oС/км в пределах коры
(0 z
z HC),
1oС/км - в пределах зоны сегрегации
(HC
HC),
1oС/км - в пределах зоны сегрегации
(HC z
z HS), где
HS = 33 км
и 0,3oС/км - в пределах адиабатической зоны в мантии
(HS
HS), где
HS = 33 км
и 0,3oС/км - в пределах адиабатической зоны в мантии
(HS z
z H),
где
(dT/dz)ad=0,3 oС/км -
адиабатический градиент температуры в
мантии. (Из других параметров, используемых в модели:
K =0,006 кал/см сoC,
rCp=0,91 кал/см3 oС,
TH = 1290oС,
H = 100 км.)
H),
где
(dT/dz)ad=0,3 oС/км -
адиабатический градиент температуры в
мантии. (Из других параметров, используемых в модели:
K =0,006 кал/см сoC,
rCp=0,91 кал/см3 oС,
TH = 1290oС,
H = 100 км.)
Решение получалось разложением искомого распределения температуры в ряды Фурье. Вдали от оси ( x = 0), где горизонтальные градиенты температур были пренебрежимы, глубины изотерм были близки к полученным в моделях [McKenzie, 1967] и [Oldenburg, 1975]. В то же время учет эффекта скрытой теплоты плавления позволил Н. Слипу более корректно описать высокотемпературный режим приосевой области океанической литосферы и даже приблизиться к имитации теплового режима подосевой магматической камеры [Sleep, 1975].
И все же в ряде деталей модель нуждалась в усовершенствовании. Прежде всего, это
касалось условий на оси рифта (5) и (6). Они предполагают отличие производной
 T/
T/ x от нуля на оси
x=0, что отражается в резком
заглублении изотерм у оси хребта с крутизной их наклона, растущим с увеличением
скорости спрединга
v [Sleep, 1975].
Это противоречит наблюдениям в СОХ, согласно которым как изотермы, так и кровля
магматического очага, в осевой области почти горизонтальны, что соответствует
условию
x от нуля на оси
x=0, что отражается в резком
заглублении изотерм у оси хребта с крутизной их наклона, растущим с увеличением
скорости спрединга
v [Sleep, 1975].
Это противоречит наблюдениям в СОХ, согласно которым как изотермы, так и кровля
магматического очага, в осевой области почти горизонтальны, что соответствует
условию
 T/
T/ x=0. Можно отметить также, что высокотемпературные
изотермы в модели, и в том числе изотерма, фиксирующая кровлю очага, располагаются
заметно ближе к поверхности дна, чем это следует из сейсмических наблюдений.
Выделение скрытой теплоты плавления в модели
[Sleep, 1975],
локализовано в коре в пределах узкой зоны на оси спрединга, причем предполагается
выделение полного объема теплоты плавления независимо от степени плавления ее
вещества (температура ликвидуса пород коры
TL вообще не участвует в
вычислениях температуры). В реальной ситуации скрытая теплота
распределяется по широкой области затвердевания пород, включающей объем и кровлю
и
края магматического очага и ее величина сильно зависит от локальной степени плавления
вещества коры.
x=0. Можно отметить также, что высокотемпературные
изотермы в модели, и в том числе изотерма, фиксирующая кровлю очага, располагаются
заметно ближе к поверхности дна, чем это следует из сейсмических наблюдений.
Выделение скрытой теплоты плавления в модели
[Sleep, 1975],
локализовано в коре в пределах узкой зоны на оси спрединга, причем предполагается
выделение полного объема теплоты плавления независимо от степени плавления ее
вещества (температура ликвидуса пород коры
TL вообще не участвует в
вычислениях температуры). В реальной ситуации скрытая теплота
распределяется по широкой области затвердевания пород, включающей объем и кровлю
и
края магматического очага и ее величина сильно зависит от локальной степени плавления
вещества коры.
 Более реальное распределение температур в осевой области с плоской кровлей
камеры были получены в последующих модификациях рассмотренной модели
[Morton and Sleep, 1985;
Sleep et al., 1983;
Wilson et al., 1988].
В этих работах эффект скрытой теплоты перенесен из граничных условий (6) в
свободный член уравнения (1), после чего граничные условия на оси имели вид (5)
для всей мощности литосферы, и температура вещества на оси
Ti изменялась с
глубиной по прежнему закону. Решение, как и раньше, искалось разложением в ряд Фурье
[Morton and Sleep, 1985]
поэтому и скрытая теплота плавления в свободном члене уравнения представлялась
через соответствующее распределение источников тепла:
Более реальное распределение температур в осевой области с плоской кровлей
камеры были получены в последующих модификациях рассмотренной модели
[Morton and Sleep, 1985;
Sleep et al., 1983;
Wilson et al., 1988].
В этих работах эффект скрытой теплоты перенесен из граничных условий (6) в
свободный член уравнения (1), после чего граничные условия на оси имели вид (5)
для всей мощности литосферы, и температура вещества на оси
Ti изменялась с
глубиной по прежнему закону. Решение, как и раньше, искалось разложением в ряд Фурье
[Morton and Sleep, 1985]
поэтому и скрытая теплота плавления в свободном члене уравнения представлялась
через соответствующее распределение источников тепла:
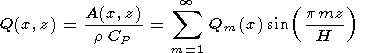 | (7) |
распределенных в виде d - функций в локальных точках: Qm(x)=Qmd(x-x0), где x0 - координата локализации источника тепла (Qm>0). Распределением 70% источников тепла, моделирующих эффект скрытой теплоты плавления вдоль кровли очага, отождествляемой в модели с изотермой Т = 1185oС, и 30% по сторонам очага авторам удалось получить стационарный коровый очаг с квазигоризонтальной формой кровли (рис. 2). Дополнительным введением над этой кровлей стоков тепла (Qm<0), имитирующих тепловое воздействие гидротермального охлаждения коры в осевой зоне, авторы модели методом итераций получают стационарное положение плоской крыши очага на глубинах, согласующихся с наблюдаемыми по сейсмическим данным ( z = 1,2-2,0 км для v = 5 см/год).
Анализируя результаты расчетов, Д. Вилсон с соавторами [Wilson et al., 1988] приходят к выводу о том, что сужение подосевого магматического очага книзу, предполагаемое из сейсмических данных, может быть объяснено лишь в рамках модели, когда температура конвертирующей магмы в очаге заметно ниже температуры солидуса материала нижней коры. В этом случае конвекция в очаге сможет охлаждать нижнюю кору и создавать очаг, расширяющийся кверху. Следует иметь в виду, что в процессе охлаждении плотность расплава после выделения и осаждения из него кристаллов, как правило, уменьшается. Следовательно, если кристаллы растут на стенках камеры или очень быстро выпадают на дно, то в верхней части камеры будет формироваться облегченный расплав, что будет способствовать подавлению конвекции в масштабах очага. Поэтому наиболее вероятной причиной конвекции в очаге может служить эпизодическое возобновление объема жидких базальтов за счет их поступления из зон сегрегации расплава на глубине. Термический аспект конвекции магмы в очаге моделируется в модели [Wilson et al., 1988] подбором стоков тепла в нижней части очага и сопряженных им источников тепла в верхней половине очага. Предпочтительная модель осевой зоны предполагает температуру вещества, поступающего в осевую зону, около 1250oС (при температуре T =1340oС на глубине z =100 км в основании области счета) и среднюю температуру магмы в очаге 1150oС (рис. 2).
Модели [Morton and Sleep, 1985] и особенно [Wilson et al., 1988], позволили оценить порядок и степень участия различных тепловых процессов в формировании термического режима осевых зон СОХ. Однако при этом нельзя не отметить их искусственный характер, так как и полученное распределение температур, и рассчитанная форма корового очага магмы в них являлись прямым результатом априорного подбора пространственного распределения источников и стоков тепла, грубо имитировавших эффекты выделения скрытой теплоты плавления и гидротермальной деятельности.
 В следующем классе моделей, получившем развитие в последние 10-15 лет,
рассматриваются двухмерные и трехмерные поля скоростей перемещения пород
литосферы и подстилающей мантии. Цель этих моделей - связать процессы
сегрегации и миграции расплава из основной мантии под срединно-океаническими
хребтами с вариациями в объеме генерированной коры и скоростью спрединга,
а также с местоположением участка в пределах изучаемого сегмента хребта.
В первых моделях этого класса
[Lin and Parmentier, 1989;
Phipps Morgan et al., 1987]
рассматривалось поле скоростей горизонтально движущейся коры и пассивного
ньютонова течения мантии (с постоянной вязкостью), индуцированного горизонтальным
движением твердой коры со скоростью
v (рис. 3а):
В следующем классе моделей, получившем развитие в последние 10-15 лет,
рассматриваются двухмерные и трехмерные поля скоростей перемещения пород
литосферы и подстилающей мантии. Цель этих моделей - связать процессы
сегрегации и миграции расплава из основной мантии под срединно-океаническими
хребтами с вариациями в объеме генерированной коры и скоростью спрединга,
а также с местоположением участка в пределах изучаемого сегмента хребта.
В первых моделях этого класса
[Lin and Parmentier, 1989;
Phipps Morgan et al., 1987]
рассматривалось поле скоростей горизонтально движущейся коры и пассивного
ньютонова течения мантии (с постоянной вязкостью), индуцированного горизонтальным
движением твердой коры со скоростью
v (рис. 3а):
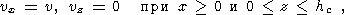 | (8) |
где hc - толщина коры, v - полускорость спрединга и
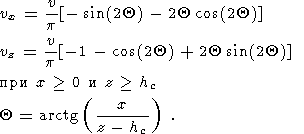 | (9) |
Стационарное уравнение теплопроводности включало члены с конвективным движением по осям x и z:
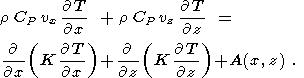 | (10) |
Уравнение решалось в области
0 x
x 140 км,
0
140 км,
0 z
z 90-100 км
с
постоянной температурой
T=TH=1200 oС в основании области счета.
Тепловой эффект высвобождения скрытой теплоты плавления в пределах корового
слоя на оси спрединга во время процесса остывания интрузий моделировался
эффективным увеличением температуры вещества интрузий до 1520oС, что
на
320oС превосходило температуру мантии на глубине. Охлаждение коры
гидротермальной конвекцией имитировалось увеличением коэффициента
теплопроводности в
Nu раз в пределах всей коры, где число Нуссельта
Nu эквивалентно отношению гидротермального потока тепла к кондуктивному
[Combarnous, 1978].
В моделях предполагалось, что породы глубже
hc=6 км или с температурой
Т выше 400oС непроницаемы для конвективных жидкостей.
90-100 км
с
постоянной температурой
T=TH=1200 oС в основании области счета.
Тепловой эффект высвобождения скрытой теплоты плавления в пределах корового
слоя на оси спрединга во время процесса остывания интрузий моделировался
эффективным увеличением температуры вещества интрузий до 1520oС, что
на
320oС превосходило температуру мантии на глубине. Охлаждение коры
гидротермальной конвекцией имитировалось увеличением коэффициента
теплопроводности в
Nu раз в пределах всей коры, где число Нуссельта
Nu эквивалентно отношению гидротермального потока тепла к кондуктивному
[Combarnous, 1978].
В моделях предполагалось, что породы глубже
hc=6 км или с температурой
Т выше 400oС непроницаемы для конвективных жидкостей.
Моделирование, проведенное в [Phipps Morgan et al., 1987] и [Lin and Parmentier, 1989], подтвердило тот факт, что гидротермальное охлаждение существенно увеличивает прочность осевой литосферы на растяжение через увеличение ее мощности. Так, для медленных хребтов (с полускоростью спрединга v =1 см/год) толщина литосферы на оси без гидротермального охлаждения составила бы всего около 2 км и оставалась бы заметно меньшей толщины коры (6 км). С учетом же гидротермального фактора с эффективным числом Нуссельта Nu =6-10 толщина литосферы медленно раздвигающихся хребтов на оси заметно превосходит толщину коры, и это согласуется с сейсмическими наблюдениями на Срединно-Атлантическом хребте. Для быстро раздвигающихся хребтов (полускорость v =5 см/год) толщина литосферы составляет около 1/2 толщины коры и с учетом гидротермального фактора. Характерно, что вдали от оси хребта распределение температур в литосфере в моделях [Phipps Morgan et al., 1987] и [Lin and Parmentier, 1989] получается близким к остывающему полупространству (рис. 3б). Эта ситуация не меняется и в модели с течением мантии с нелинейной реологией пород [Chen and Morgan, 1990], подтверждая тот факт, что температурное поле вдали от оси хребта нечувствительно к деталям течения пород в мантии.
В моделях [Barnouin-Jha et al., 1994, 1997; Chen and Phipps Morgan, 1996; Cordery and Phipps Morgan, 1992, 1993; Phipps Morgan and Chen, 1993; Sotin and Parmentier, 1989; Sparks and Parmentier, 1991, 1993; Sparks et al., 1993; Spiegelman and McKenzie, 1987] процессы генерации океанической коры и формирования термического режима литосферы, включая и образование подосевого очага магмы, связываются с механизмами миграции расплава от зон его сегрегации в мантии до осевой зоны генерации коры. Моделируемые механизмы миграции расплава отвечали двум основным условиям [Sparks and Parmentier, 1991]: 1) миграция должна быть достаточно быстрой, чтобы удалять образующийся расплав из мантии, так как нет геофизических свидетельств о присутствии на глубинах в мантии более 25% расплава; 2) должна существовать заметная горизонтальная компонента миграции, концентрирующая расплав в осевой зоне, так как чисто вертикальная миграция расплава не может обеспечить генерацию наблюдаемой мощности океанической коры в приосевой зоне. Что касается путей миграции, то предполагается, что связанная сеть каналов для миграции жидкого базальта, формируемая вдоль граней кристаллов, способна переносить жидкий расплав даже при доле плавления около 1% [Sotin and Parmentier, 1989; Sparks and Parmentier, 1991, 1993; Spiegelman and McKenzie, 1987]. Определяющая система уравнений имела вид [Spiegelman and McKenzie, 1987]:
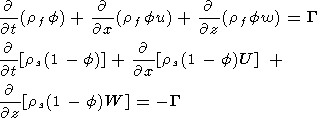 | (11) |
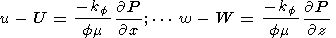 | (12) |
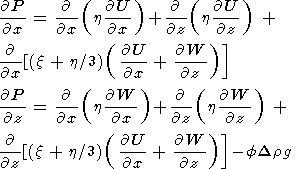 | (13) |
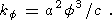 | (14) |
Здесь rf и rs - плотности расплава и твердой матрицы, u, U и w, W - горизонтальные и вертикальные составляющие скоростей расплава и твердой матрицы, G = DX/Dt - скорость генерации расплава в системе координат, фиксированной с матрицей, X - степень плавления, kf - проницаемость, связанная с пористостью f (долей объема, занятого расплавом) уравнением (14), a - средний размер зерен кристаллов, h - вязкость мантии, P - "пьезометрическое давление" ( P=p - rf gz ).
Уравнения (11) описывают закон сохранения масс для расплава и матрицы,
соответственно. Уравнение (12) - есть уравнение Дарси, которое утверждает, что скорость
выделения расплава из матрицы зависит от проницаемости и градиента
пьезометрического давления. Уравнение (13) показывает, что градиент
пьезометрического давления определяется деформациями сдвига в матрице (первый член
в правой части (13)), изменениями объема матрицы при ее расширении или
консолидации (второй член в уравнении) и разностью плотностей расплава и матрицы
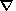 r=rs-rf. Если считать
rf и
rs заданными
и постоянными и считать известной и постоянной по величине скорость генерации
расплава
G, то решая систему уравнений (11)-(13), можно
найти пористость
f, давление
P, компоненты скоростей
u, w, U, W. В модели
[Spiegelman and McKenzie, 1987]
ситуация упрощена еще более предположением, что поле скоростей матрицы ( U и
W )
описывается аналитическим решением (8)-(9). В этом случае, принимая некоторое
среднее по области постоянное значение для пористости,
f, из уравнений
(11)-(14) можно получить аналитические выражения для компонент
скоростей движения расплава
u и
w. Существенно, что в этом решении линии
тока расплава получаются смещенными в сторону оси по отношению к расходящимся линиям
тока течения матрицы. Тем самым, М. Шпигельман и Д. Макензи показали, что
градиенты матричного давления будут фокусировать базальтовый расплав к оси. Однако
из их же работы следует, что если вязкость среды будет меньше 10
21 Па
r=rs-rf. Если считать
rf и
rs заданными
и постоянными и считать известной и постоянной по величине скорость генерации
расплава
G, то решая систему уравнений (11)-(13), можно
найти пористость
f, давление
P, компоненты скоростей
u, w, U, W. В модели
[Spiegelman and McKenzie, 1987]
ситуация упрощена еще более предположением, что поле скоростей матрицы ( U и
W )
описывается аналитическим решением (8)-(9). В этом случае, принимая некоторое
среднее по области постоянное значение для пористости,
f, из уравнений
(11)-(14) можно получить аналитические выражения для компонент
скоростей движения расплава
u и
w. Существенно, что в этом решении линии
тока расплава получаются смещенными в сторону оси по отношению к расходящимся линиям
тока течения матрицы. Тем самым, М. Шпигельман и Д. Макензи показали, что
градиенты матричного давления будут фокусировать базальтовый расплав к оси. Однако
из их же работы следует, что если вязкость среды будет меньше 10
21 Па
 с,
то этих градиентов будет недостаточно для осуществления горизонтальной миграции
расплава к оси, необходимой для генерации коры в относительно узкой приосевой
области хребта. Таким образом, необходимо искать другие эффективные механизмы
фокусировки расплава.
с,
то этих градиентов будет недостаточно для осуществления горизонтальной миграции
расплава к оси, необходимой для генерации коры в относительно узкой приосевой
области хребта. Таким образом, необходимо искать другие эффективные механизмы
фокусировки расплава.
Чтобы исправить положение, Сотин и Парментье [Sotin and Parmentier, 1989] рассмотрели новые механизмы плавучести расплава и матрицы, обусловленные термическим расширением пород и композиционным эффектом. Тогда плотность пород мантии можно записать в виде:
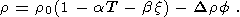 | (15) |
Здесь
a =3,5
 10
-5 oС
-1 - коэффициент термического
расширения породы.
b =0,024 - композиционное уменьшение плотности,
вызванное сокращением плотности матрицы в связи с уменьшением отношения Fe/Mg
в матрице после выделения расплава,
x - степень обеднения породы в результате
выделения расплава, член с
Dr - тот же,
что и в (13) и
обусловлен улавливанием части расплава матрицей. Композиционный член с
b при 25% выделении расплава дает то же сокращение
плотности, что и при термическом
расширении пород, вызванном увеличением температуры на 200oС. Учет термических
вариаций плотности потребовал дополнительно к системе уравнений (11-14)
рассмотрение уравнений сохранения энергии:
10
-5 oС
-1 - коэффициент термического
расширения породы.
b =0,024 - композиционное уменьшение плотности,
вызванное сокращением плотности матрицы в связи с уменьшением отношения Fe/Mg
в матрице после выделения расплава,
x - степень обеднения породы в результате
выделения расплава, член с
Dr - тот же,
что и в (13) и
обусловлен улавливанием части расплава матрицей. Композиционный член с
b при 25% выделении расплава дает то же сокращение
плотности, что и при термическом
расширении пород, вызванном увеличением температуры на 200oС. Учет термических
вариаций плотности потребовал дополнительно к системе уравнений (11-14)
рассмотрение уравнений сохранения энергии:
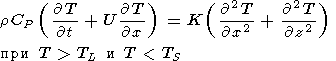 | (16) |
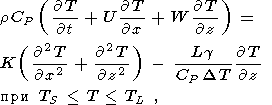 | (17) |
где L - скрытая теплота плавления, g = 3,2oС/км - градиент температуры солидуса пород мантии ( TS = 1100oС + 3,2 z ), DT = TL - TS = 200oС - для базальтового расплава. Последний член в (17) обязан выделению скрытой теплоты плавления при изменении степени плавления X вещества мантии:
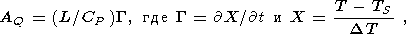 | (18) |
где G - скорость генерации расплава, как и в уравнениях (11), и степень плавления пород мантии X определялись превышением их температуры над температурой солидуса. Численное решение показало, что хотя композиционная плавучесть способствует локализации течения у оси спрединга, но область миграции расплава все еще остается заметно шире области генерации коры, оцениваемой из геофизических наблюдений. В модели [Sotin and Parmentier, 1989] отмечается также, что комбинация термической и композиционной плавучести в (15) приводит к ослаблению зависимости толщины коры от скорости спрединга. Аналогичные выводы сделаны и на основании численных расчетов в работах [Cordery and Phipps Morgan, 1992, 1993; Sparks and Parmentier, 1993]. Вместо аналитического течения (3) в этих моделях использовалось решение уравнений Навье Стокса в среде с постоянной вязкостью [Cordery and Phipps Morgan, 1992], с вязкостью, зависящей от температуры [Cordery and Phipps Morgan, 1993]:
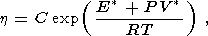 | (19) |
и с вариацией нескольких значений вязкости мантии. Однако основной вывод, сделанный на основании этих уточненных моделей, оставался прежним: рассмотренные механизмы течения не достаточны для объяснения наблюдаемой степени фокусировки течения расплава в осевой области быстро-раздвигающихся хребтов.
 Физически разумный механизм для преодоления этого противоречия
был
предложен в работе
[Sparks and Parmentier, 1991].
Ее авторы высказали предположение, что породы, находящиеся в низах литосферы
при температурах ниже солидуса, но близких к ней, являются непроницаемыми для
расплава, и что непосредственно под этим слоем формируется относительно тонкий
слой (мощностью около сотни метров и, возможно, с повышенной пористостью),
насыщенный расплавом, попавшим сюда в процессе преимущественно вертикальной
миграции расплава из низов мантии (рис. 4). Этот насыщенный расплавом слой в
основании литосферы заглубляется и отчасти расширяется с удалением от оси хребта.
Как показывает квазидвумерный анализ течения расплавленной фракции, перепад
давлений, вызванный углублением этого слоя с удалением от оси, достаточен для
фокусировки расплава, наблюдаемой по геофизическим данным в верхних горизонтах
мантии у оси СОХ
[Sparks and Parmentier, 1991].
Физически разумный механизм для преодоления этого противоречия
был
предложен в работе
[Sparks and Parmentier, 1991].
Ее авторы высказали предположение, что породы, находящиеся в низах литосферы
при температурах ниже солидуса, но близких к ней, являются непроницаемыми для
расплава, и что непосредственно под этим слоем формируется относительно тонкий
слой (мощностью около сотни метров и, возможно, с повышенной пористостью),
насыщенный расплавом, попавшим сюда в процессе преимущественно вертикальной
миграции расплава из низов мантии (рис. 4). Этот насыщенный расплавом слой в
основании литосферы заглубляется и отчасти расширяется с удалением от оси хребта.
Как показывает квазидвумерный анализ течения расплавленной фракции, перепад
давлений, вызванный углублением этого слоя с удалением от оси, достаточен для
фокусировки расплава, наблюдаемой по геофизическим данным в верхних горизонтах
мантии у оси СОХ
[Sparks and Parmentier, 1991].
Тот же вывод подтвердили Л. Магда и Д. Спаркс
[Magde and Sparks, 1997],
рассмотрев более сложный нестационарный трехмерный вариант системы уравнений
(11-18) для анализа сегрегации и миграции расплава в области 960
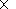 480
480
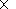 300 км.
Учитывались те же три источника плавучести пород - термическое расширение,
композиционный эффект и остаток расплава в матрице. Как и в (15), вязкость
мантии менялась с глубиной по заданному закону. Один из выводов работы гласил,
что только при учете миграции расплава вдоль верхней граничной поверхности
области плавления можно объяснить наблюдаемые вдольосевые вариации в мощности
коры и аномалиях Буге вдоль оси СОХ, тогда как более ранние попытки объяснения
этих вариаций, предпринятые в рамках трехмерных моделей без учета латеральной
миграции в работах
[Barnouin-Jha et al., 1994, 1997],
были неудачными.
300 км.
Учитывались те же три источника плавучести пород - термическое расширение,
композиционный эффект и остаток расплава в матрице. Как и в (15), вязкость
мантии менялась с глубиной по заданному закону. Один из выводов работы гласил,
что только при учете миграции расплава вдоль верхней граничной поверхности
области плавления можно объяснить наблюдаемые вдольосевые вариации в мощности
коры и аномалиях Буге вдоль оси СОХ, тогда как более ранние попытки объяснения
этих вариаций, предпринятые в рамках трехмерных моделей без учета латеральной
миграции в работах
[Barnouin-Jha et al., 1994, 1997],
были неудачными.
 В своей модели Л. Магда и Д. Спаркс
[Magde and Sparks, 1997]
исследовали также влияние сегментации СОХ на характер течения расплава и
формирование коры в их осевых зонах. Они установили, что смещение участков СОХ
по трансформным разломам делает картину течения под осевыми областями трехмерной,
причем для медленных хребтов в большей степени, чем для быстрых.
Аналогичные
трехмерные исследования с отрезками осевых зон хребтов длиной до 300 км со
смещениями по трансформным разломам до 75 км и размерами области расчета до
1200
В своей модели Л. Магда и Д. Спаркс
[Magde and Sparks, 1997]
исследовали также влияние сегментации СОХ на характер течения расплава и
формирование коры в их осевых зонах. Они установили, что смещение участков СОХ
по трансформным разломам делает картину течения под осевыми областями трехмерной,
причем для медленных хребтов в большей степени, чем для быстрых.
Аналогичные
трехмерные исследования с отрезками осевых зон хребтов длиной до 300 км со
смещениями по трансформным разломам до 75 км и размерами области расчета до
1200
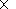 600
600
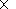 300 км (рис. 5) были предприняты в моделях
[Barnouin-Jha et al., 1994, 1997;
Sparks et al., 1993].
Модели предполагали, что предпочтительная длина волны возникающих неоднородностей
вдольосевых течений (сформированных наложением течений от движения плит и от
плавучести расплава) составляет примерно удвоенную толщину астеносферного слоя
(около 400 км). При этом расчеты показали, что восходящее течение, вызванное
раздвижением плит, будет создавать под трансформными разломами дополнительные
вдольосевые градиенты температур и степени плавления мантии, и что эти особенности
будут усиливаться плавучестью расплава, и особенно ее композиционной составляющей.
Как отмечалось выше, дестабилизирующая роль течений плавучести будет возрастать с
уменьшением скорости спрединга, так что при медленных скоростях спрединга течение
магмы под СОХ, смещенными вдоль отрезков трансформных разломов, становится
существенно трехмерным
[Sparks et al., 1993].
300 км (рис. 5) были предприняты в моделях
[Barnouin-Jha et al., 1994, 1997;
Sparks et al., 1993].
Модели предполагали, что предпочтительная длина волны возникающих неоднородностей
вдольосевых течений (сформированных наложением течений от движения плит и от
плавучести расплава) составляет примерно удвоенную толщину астеносферного слоя
(около 400 км). При этом расчеты показали, что восходящее течение, вызванное
раздвижением плит, будет создавать под трансформными разломами дополнительные
вдольосевые градиенты температур и степени плавления мантии, и что эти особенности
будут усиливаться плавучестью расплава, и особенно ее композиционной составляющей.
Как отмечалось выше, дестабилизирующая роль течений плавучести будет возрастать с
уменьшением скорости спрединга, так что при медленных скоростях спрединга течение
магмы под СОХ, смещенными вдоль отрезков трансформных разломов, становится
существенно трехмерным
[Sparks et al., 1993].
Выше отмечалось, что генеральный рельеф СОХ обязан термическому расширению пород мантии. Однако отклонения от этого генерального тренда в осевой области имеют другую природу. Ее анализа касались многие из упомянутых работ. Их авторы пытались связать природу рельефа осевых зон с вариациями в толщине литосферы. Так, в работах [Eberle and Forsyth, 1998; Neumann and Forsyth, 1993] показано, что горизонтальные растягивающие напряжения в прочной непрерывно деформируемой плите переменной мощности у оси хребта могут создавать структуры, подобные осевой долине и обрамляющим горстам за счет возникающих при растяжении моментов сил, способствующих погружению осевой части долины и воздыманию ее бортов. Более толстая, а значит и более прочная, литосфера медленно раздвигающихся хребтов будет иметь более контрастный, выраженный рельеф осевой долины, чем тонкая и слабая литосфера быстрых хребтов. При этом отмечается, что ослабленная литосфера может создаваться и при медленных скоростях спрединга под влиянием горячих мантийных пятен и вдольосевых потоков, как это имеет место, например, в Исландии и на хребте Рейкъянес, и тогда рельеф осевой долины будет выражен также слабо, как и в быстро раздвигающихся хребтах. Существенным аспектом модели осевого рельефа СОХ, рассмотренной в [Phipps Morgan et al., 1987], являются повторяющиеся внедрения расплавленного вещества в осевой зоне. В эти моменты осевая литосфера должна сильно ослабляться и вместе с этим должны быстро релаксировать состояние растяжения плиты и вызванные им напряжения, поддерживавшие осевой рельеф. Если бы плита вела себя как простое вязкое тело, то рельеф осевой долины имел бы тенденцию релаксировать в течение таких периодов резкого уменьшения состояния растяжения. Однако, как отмечает Я. Фиппс Морган с соавторами [Phipps Morgan et al., 1987], из-за того, что рельеф осевой долины создавался смещениями по разломам в периоды растяжения литосферы, а напряжений от одного лишь перепада рельефа недостаточно для возбуждения обратных движений по разломам, то релаксации рельефа будет происходить с крайне низкой скоростью и рельеф оказывается "вмороженным" в течение периодов ослабления состояния растяжения осевой океанической литосферы. По мнению авторов, эта "вмороженность" рельефа, вызванная недостаточностью напряжений от собственно рельефа для стимулирования релаксационных движений по разломам, согласуется и с наблюдениями рельефа в отмерших медленных центрах спрединга (Лабрадорский хребет, хребет Эгир в северо-восточной части Полярной Атлантики, палеоспрединговый хребет в Коралловом море). Все они сохранили рельеф осевых зон и связанные с ним гравитационные аномалии. После прекращения растяжения "вмороженный" рельеф поддерживается упругой прочностью плиты [Watts, 1982].
Нельзя не отметить, что некоторые особенности рельефа СОХ можно объяснить также образованием разуплотненных серпентинитовых тел, которые формируются всякий раз вдоль стенок трещин локального растяжения, по которым морская вода имеет возможность проникать в перидотитовые породы при температурах 250-600oС. Тектонические обстановки формирования таких трещин разнообразны: пересечения трансформных разломов и СОХ, фланги срединной долины медленных СОХ, начало или затухание спрединга и т.д. [Дубинин, 1987; Дубинин, Свешников, 2000]. Однако в пределах конкретной площади процесс серпентинизации перидотитов по трещинам выглядит относительно спорадичным и предположения о его непрерывности в пределах тех или иных площадей требует специального анализа.
Как отмечалось выше, первые модели формирования коровых очагов магмы были представлены в работах [Morton and Sleep, 1985; Sleep, 1975; Sleep et al., 1983; Wilson et al., 1988]. Анализ проблемы в них осуществлялся в рамках модели литосферы постоянной толщины с решением в виде разложения в ряды Фурье и с вариацией теплового потока и температуры на оси хребта. Подбором распределения источников и стоков тепла, имитировавших выделение скрытой теплоты плавления в процессе остывания осевых эффузивов и интрузий и вынос тепла гидротермами, авторам удалось получить распределение температур в осевой зоне близкое к наблюдаемому и воспроизвести плоскую форму кровли корового очага магмы, однако, полученные результаты нельзя считать итогом независимого моделирования.
В последующих моделях [Chen and Phipps Morgan, 1996; Henstock et al., 1993; Phipps Morgan and Chen, 1993] авторы объединили анализ широкомасштабных течений расплава и мантии с рассмотрением детальной структуры термического режима и полей деформаций приосевой коровой части хребта с целью понять природу формирования подосевого корового очага магмы.
При этом Т. Хэнсток с соавторами
[Henstock et al., 1993]
рассматривал горизонтальное поле скоростей материала приповерхностного слоя
коры в интервале глубин
0
Система стационарных уравнений неразрывности Навье-Стокса (без члена с
Dr и теплопроводности)
решалась относительно неизвестных температуры
T, давления
P и
компонент скоростей
u и
w в области
0
Вязкость среды
(h) не зависела от температуры, но изменялась
в зависимости от
глубины:
h=1018-1019 Па
Расчеты в рамках этой модели показали, что баланс тепла между четырьмя
составляющими: областью внедрения щитовых даек на оси, линзой расплава,
восходящим течением магмы и гидротермальным охлаждением коры - определяет
квазистационарное состояние линзы. В быстро раздвигающихся хребтах линза
формируется на относительно мелких уровнях в коре (1,2-2 км), заглубляется для
средних
скоростей спрединга и уходит ниже коры (т.е. исчезает) при медленных скоростях
спрединга
v<1,5 см/год. В последующей работе
[Chen and Phipps Morgan, 1996]
авторы сравнили эту модель с другой, в которой область внедрения даек занимала
всю толщину коры, а линза отсутствовала. Обе модели практически не отличались
в распределении теплового потока на оси, служившего основным критерием их
справедливости, однако, модель линзы характеризовалась более высоким уровнем
деформаций пород коры в осевой области. Как отмечают авторы, данные по строению
и составу пород в офиолитовых комплексах пока не дают возможности предпочесть
модель внедрения базальта через крышу линзы
[Phipps Morgan and Chen, 1993]
модели его внедрения в узкой дайковой зоне на оси хребта
[Chen and Phipps Morgan, 1996].
Однако и здесь к выводам модели следует относиться с осторожностью, так как
поле скоростей пород коры с их прохождением через кровлю линзы (подобно струе воды
в фонтане) и физически нереальные температуры базальта, внедряющегося на оси хребта
и в кровлю линзы ( T =1670oC), предполагают скорее качественный, чем количественный
характер рассчитанного в модели корового распределения температур и формы очага.
Как
и в предыдущих моделях, ширина линзы, а значит во многом и форма корового очага
магмы, остаются предопределенными, а не следующими из численных расчетов.
Ограничение стационарными моделями осевых зон СОХ позволило авторам
рассмотренных выше работ анализировать довольно сложные интегральные модели
формирования осевых зон, включавшие процессы сегрегации и миграции расплава к
осевой зоне, образования коры и рельефа дна. В целом, это ограничение можно
считать оправданным, так как оценки показывают, что даже эпизодические
внедрения магмы в осевую зону могут сформировать квазистационарное термическое
состояние области за исключением, быть может, района интрузий шириной 50-500 м
в самой близкой окрестности оси
[Henstock et al., 1993].
Однако временная динамика формирования термического режима осевой зоны, включая
и образование корового очага магмы, также представляет большой интерес. Поэтому
нами были разработаны нестационарные модели формирования корового очага магмы,
изложенные ниже и представленные в работах
[Галушкин, Дубинин, 1993, 1994;
Галушкин и др., 1994а; 1994б].
В наших моделях анализировался переход нестационарного поля температур,
формируемого повторяющимися внедрениями осевых интрузий (шириной 5-50 м раз
в
1000-10000 лет), в квазистационарное температурное распределение в коровом слое
осевой зоны центра спрединга. Мы максимально упростили задачу, ограничиваясь
анализом температурного поля коры и поддерживая в ее основании температуру кровли
осевого астеносферного поднятия
Т =1200oC. Условия на оси хребта ( x = 0)
в наших моделях непосредственно отражали процесс формирования корового слоя в результате
повторяющихся дайковых интрузий на оси спрединга. При этом периодически
обновляется тепловой режим осевой области. Повторяемость внедрений поддерживается
непрерывным состоянием растяжения, характерным для литосферы осевой зоны хребта.
С каждым таким внедрением связано наращивание коры на величину
D х=VDt,
где
V - средняя скорость спрединга и
Dt - интервал времени между
последовательными внедрениями. Время, которое занимает сам процесс внедрения
интрузии, обычно много меньше интервала между внедрениями, и в расчетах процесс
внедрения полагался мгновенным. Во время внедрения происходит заполнение магмой
осевой трещины полушириной
D х = VDt.
Через каждый интервал
времени
Dt процесс внедрения повторялся. При численном
моделировании
процесс внедрения интрузии воспроизводился переписыванием температуры в пределах
ширины осевой интрузии
D Х на температуру
ТМ = 1200oC.
Одновременно во всей области вне интрузии
(х>D х) распределение температуры,
существовавшее непосредственно перед внедрением, смещалось по горизонтали на
расстояние
D х. Тем самым распределение температуры всякий
раз сразу же
после внедрения интрузии
(t=ti+0) имело вид:
В интервале времени до следующего внедрения ( ti
Анализируемая модель, в отличие от рассмотренных выше, является существенно
нестационарной. Выделение скрытой теплоты при затвердевании и ее поглощение при
плавлении базальта значительно повышает тепловую инерционность среды и имеет
определяющее значение для формирования осевого очага магмы в разумные интервалы
времени. Эксперименты по затвердеванию базальтовой магмы, показывают, что степень
кристаллизации магмы является квадратичной функцией температуры в интервале между
солидусом
(TS) и ликвидусом
(ТL) базальтовых пород
[Usselman and Hodge, 1978]:
Поэтому теплоемкость пород
CP в уравнении (21) в интервале температур
TS
где
Ср - нормальная теплоемкость пород для
T
Коэффициент теплопроводности в уравнении (21) изменялся с глубиной,
расстоянием от оси спрединга и временем процесса, что существенно влияло на размеры
и форму образующегося очага магмы в коре. Отклонения этого коэффициента от
значения нормальной кондуктивной теплопроводности в коре ( K0 =6 кал/см coС),
вызванные действием конвекции, описывались, как и в моделях, рассмотренных выше,
с
помощью числа Нуссельта
Nu:
Эксперименты с породами базальтового состава показывают, что микротрещины в
базальтовых породах закрываются при температурах выше 725oС
[Hardee, 1982],
поэтому глубина этой изотермы принималась за нижнюю границу проникновения
гидротермальных вод. В области, ограниченной сверху изотермой
Т =725oС,
а снизу изотермой начала плавления базальта
Т =1150oС, фиксирующей в
нашей модели кровлю осевой камеры, доминировала кондуктивная теплопроводность.
Внутри очага число Нуссельта не должно быть высоким из-за относительно низких
долей плавления базальта, препятствующих развитию интенсивной конвекции.
Мы принимали
Nu =1,5 всюду в области ниже реологической изотермы
Т =725oС.
Таким образом, число Нуссельта, определяющее согласно (24) эффективную
теплопроводность пород, изменялась в области счета следующим образом:
т.е. на удалении от оси, где множитель
А =3-10 определял интенсивность
гидротермальной активности на оси
хребта и амплитуду ее убывания с удалением от оси хребта.
Уравнение теплопроводности (21) с начальными условиями (20) и
термофизическими параметрами пород (23-25) решалось при повторяющейся процедуре
внедрения интрузии через каждые 500-10000 лет для описания последующей релаксации
распределения температур. Шаги по осям
x и
z увеличивались по геометрической
прогрессии от минимальных значений при
x =0 и
z =0, определявшихся полушириной
интрузии (5-50 м), до максимальных 50-500 м на границе области счета. Минимальный
шаг по времени определялся устойчивостью решения ( Dt
Расчеты, представленные на рис. 7, показывают, что уменьшение полускорости
спрединга в два раза (от 5 до 2,5 см/год) приводит к заглублению очага на 1,5 км
и
уменьшению полуширины очага на 1-1,2 км. При полускорости
V = 1 см/год
стационарный осевой очаг существует в виде поднятия высотой не более 300 м на
глубине 5,5 км и не различим сейсмическими методами. За граничную полускорость,
ниже которой не существует коровый очаг, различимый геофизическими методами,
можно принять полускорость
V = 1,5 см/год. При этом поднятие кровли очага над его
крыльями не превосходит 0,5 км, а полуширина очага составляет 0,5-1 км.
Обсуждая результаты моделирования представленные на рис. 7 и 8, необходимо
остановиться на следующей проблеме. В нашей модели процесс спрединга с заданной
полускоростью
V мог быть воспроизведен интрузиями разной ширины и, соответственно,
с разной частотой внедрения. Так, спрединг с
V = 5 см/год можно смоделировать как
внедрениями интрузий с полушириной 50 м раз в 100 лет, так и внедрениями интрузий
с
полушириной 25 м раз в 500 лет, возможны и другие варианты. При этом геофизические
и геологические данные не позволяют точно выбрать вариант. Чтобы выяснить,
насколько полученные результаты зависят от принятых значений частоты внедрения
интрузий, были проведены сравнительные расчеты для полускорости спрединга
V = 5
см/год с внедрениями интрузий полушириной 5 м раз в 100 лет (5 м/100 лет),
25 м/500 лет
и 50 м/1000 лет, для
V = 2,5 см/год с внедрениями 25 м/1000 лет и 50 м/2000 лет
и для
V = 1,0 см/год с внедрениями 50 м/5000 лет и 100 м/10 000 лет.
Результаты расчетов
показали, что глубина кровли очага с точностью до 100-200 м перестает зависеть
от
ширины интрузии и соответствующей частоты внедрений по прошествии 20-25 циклов
внедрений (для максимальной ширины интрузий) с начала спрединга.
Учет образования линзы базальтового расплава относится к наиболее трудным
элементам в модифицированной модели осевого магматического очага. В нашей модели
мы пытались численно оценить термические следствия процесса формирования и
периодического обновления состава линзы расплавленного базальта в верхней части
магматического очага быстро- и среднераздвигающихся хребтов
[Галушкин и др., 1994б].
Процесс обновления линзы расплава воспроизводился в модели периодическим
переписыванием распределения температур в верхней части очага ни глубинах
Zs
Здесь
rM и
rw - плотности пород мантии
и воды. Значение
Н(х,t) оценивало превышение термического рельефа поверхности дна относительно
его
значения на правой границе области счета
(x=XM). В нашем случае вариации плотности пород коры определялись
лишь членом с температурным расширением в формуле (15). Можно заметить, что
стабилизация формы рельефа осуществляется практически за те же времена, что и
стабилизация формы камеры (рис. 7, 10). Форма рельефа остается близкой к
треугольной лишь для времен менее 70 тыс. лет с начала спрединга. Далее в осевой
зоне
вырабатывается относительно пологий участок рельефа и форма поднятия в сечении
напоминает трапецию с шириной верхней грани от 2 от 3,5 км.
Изменение термического режима пород и формы магматической камеры при ее
остывании имеет большое значение для анализа эволюции гидротермальной активности
при отмирании ветвей осевых зон спрединга, вызванном, например, перескоком оси
спрединга или существенным нарушением периодичности внедрения даек. Такие
завершающие этапы гидротермальной активности представляют особый интерес для
процесса формирования месторождений сульфидных руд, так как в этих случаях
образовавшиеся месторождения не перекрываются последующими излияниями лавовых
потоков и появляется большая вероятность их сохранения на поверхности дна океана.
Расчеты показывают, что погружение кровли камеры в ее осевой части составляет
400, 650-700, 1100-1200, 1400-1600 и 1900-2000 м после 5, 10, 20, 30 и 50 тыс.
лет
остывания очага, соответственно. После 80 тыс. лет остывания кровля камеры
погружается примерно на 2500 м, и тогда очаг становится неразличимым сейсмическими
методами. Отметим, что спад гидротермальной активности заметно
тормозит процесс
остывания очага и приводит к уменьшению амплитуды погружения кровли очага на 200-300 м
за 20-50 тыс. лет остывания. В целом же гидротермальная активность,
увеличивая теплоотдачу, сильно ускоряет остывание очага. Так, кровля очага через
40 тыс. лет остывания будет почти на 1000 м выше в варианте без гидротермального
теплообмена, чем с ним. Тяготение гидротермальной активности к центру области имеет
следствием ускоренное погружение кровли камеры у оси и отставание этого процесса
на
периферии (рис. 11).
Как показывает рис. 10б, в целом термический рельеф поверхности
дна хорошо коррелирует с формой камеры. На рис. 11 и 10б отчетливо
прослеживается усиление трапецеидальности формы кровли камеры и термического
рельефа дна океана в процессе остывания. Амплитуда термического рельефа на оси
падает примерно вдвое за времена остывания порядка 15-20 тыс. лет.
Анализ термических моделей океанической литосферы демонстрирует сложность
задачи создания универсальной модели, описывающей характерное строение и
термический режим литосферы как во фланговой, так и в осевой областях СОХ.
Если первые работы в рамках модели плиты постоянной толщины и с решениями
в виде разложения в ряды Фурье
[Сорохтин, 1973;
McKenzie, 1967;
Oldenburg, 1975;
Parker and Oldenburg, 1973;
Schubert et al., 1975]
неплохо объясняли природу генеральных черт рельефа дна океана и теплового потока
литосферы СОХ, то в описании термического состояния осевых зон СОХ они были
некорректны. В последующих модификациях этих моделей
[Sleep, 1974, 1975]
удалось избежать особенностей в распределении теплового
потока на оси хребта, однако, ограничение области выделении скрытой теплоты
плавления узкой зоной на оси спрединга в пределах коры давало в результате
распределение температур, не согласующееся с наблюдаемым в осевых зонах СОХ.
Более реальное термическое состояние осевой области с плоской кровлей
магматической камеры было получено в дальнейших модификациях этих моделей
[Morton and Sleep, 1985;
Sleep et al., 1983;
Wilson et al., 1988].
Они использовали распределенные источники и стоки тепла в осевой зоне хребта.
Однако полученное в этих моделях распределение температур и рассчитанная форма
корового очага магмы являлись прямым результатом априорного подбора пространственного
распределения источников и стоков тепла, грубо имитировавших эффекты выделения
скрытой теплоты плавления и гидротермальной деятельности, и не могли рассматриваться
как результаты независимых расчетов.
Следующий класс моделей оказался более успешным в исследовании соотношения
мощности литосферы и толщины корового слоя при разных скоростях спрединга и
роли гидротермальной деятельности
[Chen and Morgan, 1990;
Eberle and Forsyth, 1998;
Neumann and Forsyth, 1993;
Phipps Morgan et al., 1987],
а также в анализе природы вариаций мощности генерируемой коры, вызванных изменением
скорости спрединга и положения изучаемого участка осевой зоны хребта относительно
краев сегмента осевой зоны
[Barnouin-Jha et al., 1994, 1997;
Chen and Phipps Morgan, 1996;
Cordery and Phipps Morgan, 1992, 1993;
Phipps Morgan and Chen, 1993;
Sotin and Parmentier, 1989;
Sparks and Parmentier, 1991, 1993;
Sparks et al., 1993;
Spiegelman and McKenzie, 1987].
Авторы включили различные механизмы движения расплава через матрицу пород мантии,
чтобы объяснить концентрацию базальтового расплава в верхней части осевой зоны
(области генерации коры), и все же рассчитанная область миграции расплава
оставалась заметно шире области генерации коры, оцениваемой по геофизическим
данным. Чтобы преодолеть это противоречие в работе
[Sparks and Parmentier, 1991]
было высказано предположение о том, что в основании литосферы образуется слой,
насыщенный расплавом, который попадает сюда при вертикальной миграции из низов
мантии и удерживается породами в кровле этого слоя, слабая проницаемость которых
обусловлена их специфичной температурой, которая одновременно близка к солидусу
базальта, но ниже ее. Анализ показывает, что перепад давлений, вызванный
углублением этого слоя с удалением от оси хребта, достаточен для фокусировки
расплава у оси, т.е. для создания здесь источников расплавленного базальта,
необходимого для генерации базальтовой коры
[Sparks and Parmentier, 1991].
Учет миграции расплава вдоль верхней граничной поверхности этой области плавления
помог объяснить и вариации в мощности коры и аномалиях Буге, наблюдаемые вдоль оси
СОХ
[Magde and Sparks, 1997].
Те же исследования установили, что смещение участков СОХ по трансформным разломам
делает картину течения под осевыми областями трехмерной, причем для медленных
хребтов в большей степени, чем для быстрых.
В работах
[Chen and Phipps Morgan, 1996;
Henstock et al., 1993;
Phipps Morgan and Chen, 1993]
была сделана попытка применить полученные выше результаты для
объяснения природы формирования подосевого корового очага магмы. Они объединили
анализ широкомасштабных течений расплава и мантии с рассмотрением детальной
структуры термического режима и полей деформаций приосевой коровой части хребта.
Авторы показали, что в рамках стационарной модели можно подобрать такое
распределение источников расплавленного базальта и тепла в осевой области внутри
корового слоя, которое отвечало бы устойчивому существованию здесь магматического
очага при больших и средних скоростях спрединга. Однако поле скоростей
расплавленного базальта, использованное в модели, с прохождением базальта через
кровлю линзы, подобно струе воды в фонтане, и температуры этого базальта
T =1670oC,
выглядят экзотическими, и предполагают скорее качественный, чем количественный
характер рассчитанного в модели корового распределения температур и формы очага.
Как
и в предыдущих моделях, размеры линзы расплава, а значит во многом и форма корового
очага магмы, остаются предопределенными, и не следуют из численных расчетов.
В целом, стационарные модели термического состояния осевых зон СОХ
позволили провести анализ довольно сложных 2-х и 3-х мерных интегральных моделей
формирования термического режима осевых зон с учетом процессов сегрегации и
миграции расплава к осевой зоне, образования коры и рельефа поверхности литосферы.
Однако тепловой эффект выделения или поглощения скрытой теплоты плавления
базальта трактуется в них очень грубо: через условия на тепловой поток на оси хребта,
априорное задание источников и стоков тепла в осевой зоне и через задание нереально
высоких температур расплава. По этой причине стационарные модели не подходят для
анализа эволюции термического режима осевой зоны хребтов, возникновения и развития
коровых очагов магмы, так как в указанных процессах поглощение скрытой теплоты при
плавлении пород и выделение ее при их затвердевании играет определяющую роль. Эти
же процессы определяют и существенную нестационарность моделей формирования
корового очага магмы
[Галушкин, Дубинин, 1993, 1994;
Галушкин и др., 1994а, 1994б].
Разработанная нами модель позволила численно воспроизвести процесс перехода
нестационарного поля температур, формируемого повторяющимися внедрениями осевых
интрузий (шириной 5-50 м раз в 1000-10000 лет), в квазистационарное температурное
распределение в коровом слое осевой зоны центра спрединга. Наш анализ подтвердил
выводы предшествующих работ о том, что скорость спрединга (частота внедрений в
нашей модели), наряду с гидротермальным теплообменом в коре имеют определяющее
значение для образования и существования корового очага магмы и эволюции его
формы. В частности, при малой частоте внедрения интрузии, отвечающей полускоростям
спрединга меньшим 1,5 см/год, существование устойчивого корового очага магмы
маловероятно. Перерыв между внедрениями в 100 тыс. лет и более также приводит к
исчезновению магматической камеры. Наличие линзы расплавленного базальта с
периодически обновляемым составом, расположенной в верхней части магматической
камеры помогает объяснить плоский характер кровли осевой камеры.
Рассмотренная модель дала возможность в первом приближении представить
пространственно-временной масштаб процессов формирования осевой коровой
магматической камеры и термического состояния корового слоя осевой зоны СОХ. Как
и
предшествующие модели, она безусловно нуждается в усовершенствовании. Оно видится
в следующих шагах: 1) расширение области счета по глубине с 6 до 100 км;
2) состыковка решения для дискретного спрединга коры с решением непрерывного
течения
несжимаемой мантии в клине; 3) выбор подходящей температуры внедрения базальтовых
коровых интрузий на оси (температура порядка ликвидуса базальта); 4) подбор
кривой
солидуса базальта, возможно как функция состава магмы; 5) более тщательный подбор
кривой солидуса вещества мантии для определения подошвы литосферы; 6) анализ
соотношения толщины коры и литосферы при разных скоростях спрединга; 7) рассмотрение
линзы расплава в очаге как аналога подлитосферного слоя, обогащенного
расплавом.
Таким образом, несмотря на большое число имеющихся моделей, решение
проблемы формирования термического режима осевых областей СОХ, возникновения и
эволюции осевых коровых очагов магмы еще далеко от завершения.
Галушкин Ю. И., Дубинин Е. П., Модель образования и развития магматической камеры
рифтовых зон срединно-океанических хребтов, ДАН РАН, 332, (4), 496-499, 1993.
Галушкин Ю. И., Дубинин Е. П., Магматическая камера рифтовых зон
срединно-океанических хребтов: термическая модель формирования и эволюции,
Вулканология и сейсмология, (4-5), 90-98, 1994.
Галушкин Ю. И., Дубинин Е. П., Шеменда А. И., Термическая структура осевой
зоны
срединно-океанического хребта, Статья 1, Формирование и эволюция осевой
магматической камеры, Изв. АН РАН, Сер. Физика Земли, (5), 11-19, 1994а.
Галушкин Ю. И., Дубинин Е. П., Шеменда А. И., Термическая структура осевой
зоны
срединно-океанического хребта, Статья 2, Влияние линзы расплава на форму и
эволюцию магматической камеры, Изв. АН РАН, Сер. Физика Земли, (5), 19-26,
1994б.
Дубинин Е. П., Трансформные разломы океанической литосферы, 180 c.,
Московский ун-т, Москва, 1987.
Дубинин Е. П., Свешников А. А., Эволюция литосферы палеоспрединговых хребтов,
(Результаты математического моделирования), Геотектоника, (3), 72-90, 2000.
Карслоу Г., Егер Д., Теплопроводность твердых тел, c. 487, Наука, Москва,
1964.
Сорохтин О. Г., Зависимость топографии срединно-океанических хребтов от скорости
раздвижения литосферных плит, ДАН СССР, 208, (6), 1338-1341, 1973.
Теркот Д., Шуберт Дж., Геодинамика, 731 c., Мир, Москва, 1985.
Ушаков С. А., Галушкин Ю. И., Дубинин Е. П., Гапоненко Г. И.,
Иванов О. П.,
Иванов С. С., Каверзнев К. М., Шимараев В. Н.,
Гравитационное поле и рельеф дна Мирового океана, 296 c., Недра, Л., 1979.
Barnouin-Jha K., Parmentier E. M. and Phipps Morgan J., The role of mantle-depletion
and
melt-retention buoyancy in spreading-center segmentation, Earth Planet. Sci.
Lett., 125, 221-234, 1994.
Barnouin-Jha K., Parmentier E. M. and Sparks D. W., Buoyant mantle upwelling
and crustal
production at oceanic spreading centers: on-axis segmentation and off-axis melting,
J. Geophys. Res., 102, (B6), 11,979-11,989, 1997.
Chen Y. and Morgan W. J., A nonlinear rheology model for mid-oceanic ridge axis topography,
J. Geophys. Res., 95, 17,583-17,604, 1990.
Chen Y. J. and Phipps Morgan J., The effect of spreading rate, the magma budget,
and the
geometry of magma emplacement on the axial heat flux at mid-oceanic ridges,
J. Geophys. Res., 101, (B5), 11,475-11,482, 1996.
Combarnous M., Natural convection in porous media and geothermal systems, in:
Int. Heat Transfer Conf., 6-th, p. 45-59, 1978.
Cordery M. J. and Phipps Morgan J., Melting and mantle flow beneath a mid-oceanic
spreading
center, Earth Planet. Sci. Lett., 111, 493-516, 1992.
Cordery M. J. and Phipps Morgan J., Convection and melting at mid-oceanic ridges,
J. Geophys. Res., 98, (B11), 19,477-19,503, 1993.
Eberle M. A. and Forsyth D. W., An alternative, dynamic model of the axial topographic
high at
fast spreading ridges, J. Geophys. Res., 103, (B6), 12,309-12,320, 1998.
Hardee H. C., Permeable convection above magma bodies, Tectonophysics, 84,
179-195, 1982.
Henstock T. J., Woods A. W. and White R. S., The accretion of oceanic crust
by episodic dill
intrusion, J. Geophys. Res., 98, (B3), 4143-4161, 1993.
Kieffer S. W., Lattice thermal conductivity within the Earth and consideration of
a relationship
between the pressure dependence of the thermal diffusity and the volume dependence
of the
Greeneisen parameter, J. Geophys. Res., 81, 3025-3030, 1976.
Lin J. and Parmentier E. M., Mechanisms of lithosphere extension at mid-oceanic ridges,
Geophys. J., 96, 1-22, 1989.
MacDonald G. J., Calculations of the thermal history of the Earth,
J. Geophys. Res., 64, (11), 1967-2000, 1959.
Magde L. S. and Sparks D. W., Three-dimensional mantle upwelling, melt generation,
and melt
migration beneath segment slow spreading ridges, J. Geophys. Res., 102, (B9),
20,571-20,583, 1997.
Makhous M., Galushkin Yu. I. and Lopatin N. V., Burial history and kinetic
modelling for
hydrocarbon generation, Part I: The GALO Model, AAPG Bull., 81, (10), 1660-1678,
1997.
McKenzie D. P., Some remarks on heat-flow and gravity anomalies,
J. Geophys. Res., 72, (24), 1967.
McKenzie D. and Weiss N., Speculations on the thermal and tectonic history of the
Earth,
Geophys. J. Roy. Astron. Soc., 42, p. 131, 1975.
Morton J. L. and Sleep N. H., A mid-oceanic ridge thermal model constraints on the
volume of
axial hydrothermal heat flux, J. Geophys. Res., 90, (B13), 11,345-11,353,
1985.
Neumann G. A. and Forsyth D. W., The paradox of the axial profile: isostatic compensation
along the axis of the Mid-Atlantic Ridge, J. Geophys. Res., 98, (B10), 17,891-17,910,
1993.
Oldenburg D. W., A physical model for the creation of the lithosphere,
Geophys. J. Roy. Astr. Soc., 43, p. 425, 1975.
Parker R. L. and Oldenburg D. W., Thermal model of oceanic ridges,
Nature Physics Sci., 242, p. 137, 1973.
Parson B. and Sclater I. C., An analysis of the variation of oceanic floor bathimetry
and heat
flow with age, J. Geophys. Res., 82, 803-820, 1977.
Phipps Morgan J. and Chen Y. J., The genesis of oceanic crust: magma injection, hydrothermal
circulation, and crustal flow, J. Geophys. Res., 98, (B4), 6283-6297, 1993.
Phipps Morgan J., Parmentier E. M. and Lin J., Mechanisms for the origin of
mid-oceanic ridge
topography: implications for the thermal and mechanical structure of accreting plate
boundaries, J. Geophys. Res., 92, (B12), 12,823-12,836, 1987.
Schatz J. F. and Simmons G., Thermal conductivity of Earth materials at high temperatures,
J. Geophys. Res., 77, (35), 6966-6983, 1972.
Schubert G., Froidevaux C. and Yuen D. A., Oceanic lithosphere and astenosphere:
thermal and
mechanical structure, J. Geophys. Res., 81, p. 3525, 1975.
Sleep N. H., Segretation of magma from a mostly crystalline mush,
Geol. Soc. Amer. Bull., 85, p. 1225, 1974.
Sleep N. H., Formation of oceanic crust: some thermal constraints,
J. Geophys. Res., 80, p. 4037, 1975.
Sleep N. H., Morton J. L., Burns L. E. and Wolery Th. J., Geophysical
constraints of the volume
of hydrothermal flow at ridge axis, in: Hydrothermal processes at sea floor spreading
centers; NATO conference marine sciences 12, ed. by Rona P. A. et al.,
p. 53-68,
New York, 1983.
Sotin C. and Parmentier E. M., Dynamical consequences of compositional and thermal
density
stratification beneath spreading centers, Geophys. Res. Letters, 16, (8),
835-838, 1989.
Sparks D. W. and Parmentier E. M., Melt extraction from the mantle beneath spreading
centers,
Earth Planet. Sci. Lett., 105, 368-377, 1991.
Sparks D. W. and Parmentier E. M., The structure of three-dimensional convection
beneath
oceanic spreading centers, Geophys. J. Int., 112, 81-91, 1993.
Sparks D. W., Parmentier E. M. and Phipps Morgan J., Three-dimensional mantle
convection
beneath a segmented spreading center: implications for along-axis variations in crustal
thickness and gravity, J. Geophys. Res., 98, (B12), 21,977-21,995, 1993.
Spiegelman M. and McKenzie D., Simple 2-D models for melt extraction at mid-ocean
ridges
and island arcs, Earth Planet. Sci. Lett., 83, 137-152, 1987.
Ungerer P., Burrus I., Doligez B., Chenet P. and Bessis F., Basin
evolution by integrated
two-dimensional modelling of heat transfer, fluid flow, hydrocarbon generation,
and migration, AAPG Bull., 74, (3), 309-335, 1990.
Usselman T. M. and Hodge D. S., Thermal control of low-pressure of reactionation
processes,
J. Volcan. Geotherm., Res., 4, 265-281, 1978.
Watts A. B., Gravity anomalies over oceanic rifts, in: Oceanic and continental
rifts, Geodyn. ser., ed. by G. Palmason, v. 8, p. 99-106,
AGU, Washington, D.C., 1982.
Wilson D. S., Clague D. A., Sleep N. H. and Morton J. L., Implications
of magma convection for
the size and temperature of magma chambers at fast spreading ridges,
J. Geophys. Res., 93, (B10), 11,974-11,984, 1988.
 Более корректные модели формирования корового очага магмы представлены в работах
[Chen and Phipps Morgan, 1996;
Phipps Morgan and Chen, 1993].
В них основное внимание концентрировалось на температурном поле коровой осевой
зоны хребта, поэтому процессы плавучести и сегрегации расплава (формулы (13),
(15)) не рассматривались. Движение расплава не отделялось от деформаций матрицы
и, тем самым, два уравнения неразрывности (11) вырождались в одно. Рассчитывалось
поле скоростей вязкой несжимаемой ньютоновой жидкости, индуцированное движением
твердой литосферной плиты и действием двух источников масс: в области щитовых даек
0
Более корректные модели формирования корового очага магмы представлены в работах
[Chen and Phipps Morgan, 1996;
Phipps Morgan and Chen, 1993].
В них основное внимание концентрировалось на температурном поле коровой осевой
зоны хребта, поэтому процессы плавучести и сегрегации расплава (формулы (13),
(15)) не рассматривались. Движение расплава не отделялось от деформаций матрицы
и, тем самым, два уравнения неразрывности (11) вырождались в одно. Рассчитывалось
поле скоростей вязкой несжимаемой ньютоновой жидкости, индуцированное движением
твердой литосферной плиты и действием двух источников масс: в области щитовых даек
0 x
x 250 м,
0
250 м,
0 z
z d=500-800 м
и в области линзы расплава
0
d=500-800 м
и в области линзы расплава
0 x
x 1 км,
d
1 км,
d z
z d+250 м. В первой области масса коры генерировалась со скоростью
dy/dt=rvd/d
250 м и во второй со скоростью
dy/dt=v(HC-d)r/1 км250 м на единицу объема
(единицу площади области). Генерация массы в области щитовых даек обеспечивала
однородную горизонтальную скорость раздвижения коры в интервале глубин
0
d+250 м. В первой области масса коры генерировалась со скоростью
dy/dt=rvd/d
250 м и во второй со скоростью
dy/dt=v(HC-d)r/1 км250 м на единицу объема
(единицу площади области). Генерация массы в области щитовых даек обеспечивала
однородную горизонтальную скорость раздвижения коры в интервале глубин
0 z
z d
. Генерация массы в пределах линзы обеспечивала расходящееся к низу
течение в остальном интервале глубин коры
d
d
. Генерация массы в пределах линзы обеспечивала расходящееся к низу
течение в остальном интервале глубин коры
d z
z HC=6 км, которое на
глубине подошвы коры сопрягалось с течением мантии в клине (9) и при
х
HC=6 км, которое на
глубине подошвы коры сопрягалось с течением мантии в клине (9) и при
х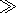 HC переходило в горизонтальный
спрединг коры с полускоростью
v (рис. 6).
Таким
образом, предполагалось, что вся масса коры ниже щитовых даек
(z>d) должна
была проходить через линзу. Тепловой эффект выделения скрытой теплоты плавления
базальтовых пород, формирующих кору, при их затвердевании, учитывался заданием
повышенной температуры внедряющегося базальта на оси
x = 0 и
0
HC переходило в горизонтальный
спрединг коры с полускоростью
v (рис. 6).
Таким
образом, предполагалось, что вся масса коры ниже щитовых даек
(z>d) должна
была проходить через линзу. Тепловой эффект выделения скрытой теплоты плавления
базальтовых пород, формирующих кору, при их затвердевании, учитывался заданием
повышенной температуры внедряющегося базальта на оси
x = 0 и
0 z
z d
и на крыше линзы
z=d и
0
d
и на крыше линзы
z=d и
0 x
x 1 км.
Считалось, что эта температура на
величину
DT=L/CP=(80 кал/г)/(0,25 кал/гo
C) = 320oC должна
превышать температуру мантии на глубине, т.е. температуру, поддерживаемую в
основании области счета ( T = 1350oC при
z = 90 км)
[Phipps Morgan and Chen, 1993].
1 км.
Считалось, что эта температура на
величину
DT=L/CP=(80 кал/г)/(0,25 кал/гo
C) = 320oC должна
превышать температуру мантии на глубине, т.е. температуру, поддерживаемую в
основании области счета ( T = 1350oC при
z = 90 км)
[Phipps Morgan and Chen, 1993].
 x
x 140 км,
0
140 км,
0 z
z 90 км.
Граничные условия предполагали отсутствие касательных напряжений
(ss) и
равенство нулю температуры и вертикальной компоненты скорости перемещений на верхней
поверхности ( T = 0oC,
ss =0,
w =0 при
z =0 и
0
90 км.
Граничные условия предполагали отсутствие касательных напряжений
(ss) и
равенство нулю температуры и вертикальной компоненты скорости перемещений на верхней
поверхности ( T = 0oC,
ss =0,
w =0 при
z =0 и
0 x
x 140 км),
отсутствие напряжений в основании области счета ( T = 1350oC,
ss=0, sn=0
при
z = 90 км и
0
140 км),
отсутствие напряжений в основании области счета ( T = 1350oC,
ss=0, sn=0
при
z = 90 км и
0 x
x 140 км),
условия симметрии на оси
(
140 км),
условия симметрии на оси
(  T/
T/ x=0,
x=0,  ss/
ss/ x=0,
x=0,  sn/
sn/ x=0 при
x=0 ), горизонтальность изотерм и переход линий тока на правой границе
области счета в
аналитическое решение клина (
x=0 при
x=0 ), горизонтальность изотерм и переход линий тока на правой границе
области счета в
аналитическое решение клина (  T/
T/ x=0, u=UP(x,z) и
w=WP(x,z) при
x =140 км). Выше
ss, sn
- касательное и нормальное
напряжения,
UP(x,z) и
WP(x,z) - горизонтальная и вертикальная составляющие
аналитического решения для течения несжимаемой жидкости в клине (8)-(9).
x=0, u=UP(x,z) и
w=WP(x,z) при
x =140 км). Выше
ss, sn
- касательное и нормальное
напряжения,
UP(x,z) и
WP(x,z) - горизонтальная и вертикальная составляющие
аналитического решения для течения несжимаемой жидкости в клине (8)-(9).
 с - в астеносфере (ниже литосферы),
h=h лит=1022-1023 Пас
- в литосфере,
h=1015-1016 Па
с - в астеносфере (ниже литосферы),
h=h лит=1022-1023 Пас
- в литосфере,
h=1015-1016 Па
 с - в
горячей коре ( T>750 oC), холодная кора ( T<750 oC) имела
вязкость литосферы. Кроме того в коре выделялась область инжекции даек:
0
с - в
горячей коре ( T>750 oC), холодная кора ( T<750 oC) имела
вязкость литосферы. Кроме того в коре выделялась область инжекции даек:
0 x
x 250 м,
0
250 м,
0 z
z z750,
где
z750 - глубина изотермы
T =750oC. В этой области
h=h лит/10=1021-1022 Па
z750,
где
z750 - глубина изотермы
T =750oC. В этой области
h=h лит/10=1021-1022 Па
 с.
Подошва литосферы определялась глубиной изотермы
T=750 oC. Предполагалось,
что в пределах коры в области
0
с.
Подошва литосферы определялась глубиной изотермы
T=750 oC. Предполагалось,
что в пределах коры в области
0 z
z 6 км
и при
T
6 км
и при
T 600 oC существенно
действие гидротермального охлаждения, так что теплопроводность этих участков коры
превосходила нормальную проводимость коры
k0=0,006 кал/(см сoC) в
Nu раз
( Nu =8-10). Теплопроводность пород мантии принималась равной
k = 0,008 кал/(см сoC).
600 oC существенно
действие гидротермального охлаждения, так что теплопроводность этих участков коры
превосходила нормальную проводимость коры
k0=0,006 кал/(см сoC) в
Nu раз
( Nu =8-10). Теплопроводность пород мантии принималась равной
k = 0,008 кал/(см сoC).
Формирования корового осевого очага магмы в нестационарной
модели
эпизодического спрединга
а) Постановка задачи и методы решения
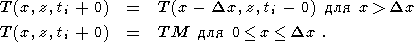
(20) 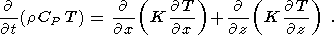
(21) 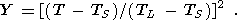
(22) 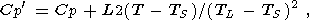
(23) 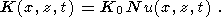
(24) 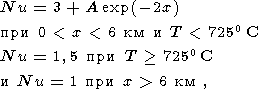
(25)  Dx2, Dz2/k, где
k=K/rCP )
и
зависел от ширины осевых интрузий и эффективной теплопроводности. В промежутках
между внедрениями в самом начале релаксации он мог быть менее 1 года, но затем по
прошествии 10-20 шагов после внедрения мог быть увеличен в 1,5-3 раза. Расчеты
показали, что формирование устойчивой структуры осевой камеры происходит по
прошествии 50-100 внедрений после начала первого из них.
Dx2, Dz2/k, где
k=K/rCP )
и
зависел от ширины осевых интрузий и эффективной теплопроводности. В промежутках
между внедрениями в самом начале релаксации он мог быть менее 1 года, но затем по
прошествии 10-20 шагов после внедрения мог быть увеличен в 1,5-3 раза. Расчеты
показали, что формирование устойчивой структуры осевой камеры происходит по
прошествии 50-100 внедрений после начала первого из них.
 Основной результат моделирования, представленный на рис. 7, состоит в
демонстрации возможности формирования корового магматического очага в процессе
повторяющихся осевых интрузий и анализе изменения глубины и формы очага в
зависимости от скорости спрединга. Однако прежде чем перейти к обсуждению
результатов, необходимо отметить, что в нашей постановке задачи стационарной
(асимптотической) формы магматической камеры, строго говоря, не существует. Форма
камеры меняется непрерывно, но по прошествии времени, эти изменения становятся
заметными лишь в самых далеких крыльях. Поэтому можно ввести понятие
асимптотической или "стационарной" формы камеры, понимая под ней ту форму,
которая устанавливается за времена порядка 0,2-0,3 млн лет, сравнимые с геологическим
Основной результат моделирования, представленный на рис. 7, состоит в
демонстрации возможности формирования корового магматического очага в процессе
повторяющихся осевых интрузий и анализе изменения глубины и формы очага в
зависимости от скорости спрединга. Однако прежде чем перейти к обсуждению
результатов, необходимо отметить, что в нашей постановке задачи стационарной
(асимптотической) формы магматической камеры, строго говоря, не существует. Форма
камеры меняется непрерывно, но по прошествии времени, эти изменения становятся
заметными лишь в самых далеких крыльях. Поэтому можно ввести понятие
асимптотической или "стационарной" формы камеры, понимая под ней ту форму,
которая устанавливается за времена порядка 0,2-0,3 млн лет, сравнимые с геологическим
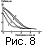 временем существования подобных структур (0,5-1 млн лет). Кривые на рис. 8
иллюстрируют процесс приближения формы магматической камеры к "стационарной".
Здесь показан пример с полускоростью раскрытия
V = 2,5 см/год, хотя он характерен для
всех рассмотренных скоростей раскрытия. Во всех случаях уже через 100-150 тыс. лет
после начала спрединга (т.е. после 40-60 внедрений магмы на оси спрединга) форма
камеры, за исключением своих далеких крыльев, отличалась от асимптотической не более
чем на 5%.
временем существования подобных структур (0,5-1 млн лет). Кривые на рис. 8
иллюстрируют процесс приближения формы магматической камеры к "стационарной".
Здесь показан пример с полускоростью раскрытия
V = 2,5 см/год, хотя он характерен для
всех рассмотренных скоростей раскрытия. Во всех случаях уже через 100-150 тыс. лет
после начала спрединга (т.е. после 40-60 внедрений магмы на оси спрединга) форма
камеры, за исключением своих далеких крыльев, отличалась от асимптотической не более
чем на 5%.
в) Влияние линзы базальтового расплава на форму
и эволюцию осевой
магматической камеры
 Результаты численного моделирования приведены на рис. 9. Здесь
представлен
пример моделирования осевой камеры в коре быстро раздвигающегося хребта с
V=5 см/год (внедрения даек полушириной 50 м раз в 1000 лет, или полушириной
5 м раз в
100 лет). Считалось, что процесс обновления состава линзы расплава в верхней части
очага происходил не чаще этих внедрений (линза расплава толщиной 350 м обновлялась
с температурой
Т лнз = 1200oC). На рисунке показано становление формы камеры
от момента начала внедрений при
t =0 до "квазистационарного" положения кровли на время
t =280 тыс. лет. Кровля камеры, располагающаяся в варианте без линзы на глубине
2,4-2,5 км (рис. 7), имеет теперь выраженный плоский участок полушириной
1,7-1,9 км (рис. 9).
Характерно, что, как и ранее, изменения в форме кровли камеры по прошествии 200
тыс. лет с начала спрединга, заметны лишь в крыльях камеры. Анализ показал также,
что изменение периода обновления состава линзы
Dtл, ее температуры
Тлн и мощности
dлнз имеют заметное влияние на результаты
моделирования. Так, уменьшение
Dt л от 500 до 200 лет приводило
к
уменьшению глубины кровли камеры примерно на 400 м; падение температуры обновляемого
вещества линзы
Тлн на 25oС - к увеличению глубины кровли камеры на 200-250 м
и одновременному сужению ее в верхней части, тогда как уменьшение мощности линзы
с
350 до 250 м относительно слабо сказалось на глубине камеры, но заметно сузило
ее
[Галушкин и др., 1994б].
Результаты численного моделирования приведены на рис. 9. Здесь
представлен
пример моделирования осевой камеры в коре быстро раздвигающегося хребта с
V=5 см/год (внедрения даек полушириной 50 м раз в 1000 лет, или полушириной
5 м раз в
100 лет). Считалось, что процесс обновления состава линзы расплава в верхней части
очага происходил не чаще этих внедрений (линза расплава толщиной 350 м обновлялась
с температурой
Т лнз = 1200oC). На рисунке показано становление формы камеры
от момента начала внедрений при
t =0 до "квазистационарного" положения кровли на время
t =280 тыс. лет. Кровля камеры, располагающаяся в варианте без линзы на глубине
2,4-2,5 км (рис. 7), имеет теперь выраженный плоский участок полушириной
1,7-1,9 км (рис. 9).
Характерно, что, как и ранее, изменения в форме кровли камеры по прошествии 200
тыс. лет с начала спрединга, заметны лишь в крыльях камеры. Анализ показал также,
что изменение периода обновления состава линзы
Dtл, ее температуры
Тлн и мощности
dлнз имеют заметное влияние на результаты
моделирования. Так, уменьшение
Dt л от 500 до 200 лет приводило
к
уменьшению глубины кровли камеры примерно на 400 м; падение температуры обновляемого
вещества линзы
Тлн на 25oС - к увеличению глубины кровли камеры на 200-250 м
и одновременному сужению ее в верхней части, тогда как уменьшение мощности линзы
с
350 до 250 м относительно слабо сказалось на глубине камеры, но заметно сузило
ее
[Галушкин и др., 1994б].
 На рис. 10 показан термический рельеф дна над коровой камерой,
созданный
температурным влиянием камеры и вмещающих ее пород. Этот рельеф вычисляется в
рамках гипотезы локального изостатического равновесия из условия равенства весов
столбцов коры с основанием (уравнением изостазии) на глубине
z=ZM (уравнением
изостазии):
На рис. 10 показан термический рельеф дна над коровой камерой,
созданный
температурным влиянием камеры и вмещающих ее пород. Этот рельеф вычисляется в
рамках гипотезы локального изостатического равновесия из условия равенства весов
столбцов коры с основанием (уравнением изостазии) на глубине
z=ZM (уравнением
изостазии):
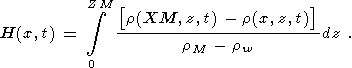
(26) г) Эволюция магматической камеры при ее остывании
 Динамика процесса релаксации термического режима остывающего
магматического очага демонстрируется на рис. 11. Здесь представлен вариант, когда
исходная форма очага перед началом релаксации (остывания) соответствовала времени
t =280 тыс. лет на рис. 9. В расчетах учитывался как факт погружения нижней границы
проникновения гидротерм вслед за "реологической" изотермой
Т =725oС, так и
уменьшение интенсивности гидротермальной деятельности по мере остывания очага.
Уменьшение интенсивности связано с тем, что по мере остывания очага ширина зоны
кондуктивной теплопроводности, ограниченной сверху реологической изотермой
Т =725oС,
а снизу изотермой солидуса базальта
Т =1150oС, увеличивается, и, соответственно,
уменьшается (почти обратно пропорционально ширине зоны
d(x,t) ) тепловой поток через
эту зону, питающий гидротермальную активность. В расчетах этот процесс
моделировался изменением числа Нуссельта в области выше реологической изотермы
как:
Nu
Динамика процесса релаксации термического режима остывающего
магматического очага демонстрируется на рис. 11. Здесь представлен вариант, когда
исходная форма очага перед началом релаксации (остывания) соответствовала времени
t =280 тыс. лет на рис. 9. В расчетах учитывался как факт погружения нижней границы
проникновения гидротерм вслед за "реологической" изотермой
Т =725oС, так и
уменьшение интенсивности гидротермальной деятельности по мере остывания очага.
Уменьшение интенсивности связано с тем, что по мере остывания очага ширина зоны
кондуктивной теплопроводности, ограниченной сверху реологической изотермой
Т =725oС,
а снизу изотермой солидуса базальта
Т =1150oС, увеличивается, и, соответственно,
уменьшается (почти обратно пропорционально ширине зоны
d(x,t) ) тепловой поток через
эту зону, питающий гидротермальную активность. В расчетах этот процесс
моделировался изменением числа Нуссельта в области выше реологической изотермы
как:
Nu 1/d(x,t).
1/d(x,t). Заключение
Благодарности
Работа выполнена при поддержке РФФИ (проект № 00-05-64399) и ФЦП
"Интеграция" (проект № 2.1-А0070).
Литература
Загрузка файлов для печати и локального просмотра.
This document was generated by TeXWeb
(Win32, v.1.0) on February 10, 2001.