
А. А. Бурцев, М. Н. Жижин
Институт физики Земли РАН
В связи с наличием большого количества ценных аналоговых записей землетрясений (до конца 60-х годов в аналоговом виде записывались все сейсмические события), а также в силу недолговечности традиционных носителей (бумага, микрофильмы) возникает необходимость перевода этих записей в электронный вид. Возможно хранение их на компьютере в виде графических файлов, однако это не позволяет исследовать их стандартными средствами анализа временных рядов. Кроме того, требуется в сотни раз большее количество ресурсов для хранения и передачи изображений записей, чем их цифрового представления. В связи с этим становится актуальной задача распознавания и оцифровки сигнала на этих изображениях (т.е. реконструкции записи по ее изображению).
Исходные данные в этой задаче - изображение следа, полученного в результате движения чернильного пера самописца по бумаге (возможны другие варианты: светового луча по фотобумаге, иглы по закопченному барабану). Требуется реконструировать этот след в виде временного ряда, описывающего зависимость амплитуды отклонения от времени.
Существуют четыре основные проблемы, которые необходимо решить для успешного нахождения траектории движения пера самописца (перечислены в порядке их возникновения):
 Для решения вышеперечисленных проблем разработан алгоритм
реконструкции следа самописца по изображению, включающий пять этапов
(рис. 1).
На первом, мы приводим исходное изображение к двухцветному
(черно-белому) виду, после чего на втором этапе находим его скелет и выделяем
примитивы, из которых он состоит. На третьем шаге корректируем выбранные
примитивы, с целью приведения их к гладкому виду. На четвертом этапе,
методом динамического программирования, отбираем только необходимые для
построения следа примитивы, по которым строим окончательный вариант
кривой. На пятом, заключительном этапе, пересчитываем полученную
траекторию в физические единицы измерения.
Для решения вышеперечисленных проблем разработан алгоритм
реконструкции следа самописца по изображению, включающий пять этапов
(рис. 1).
На первом, мы приводим исходное изображение к двухцветному
(черно-белому) виду, после чего на втором этапе находим его скелет и выделяем
примитивы, из которых он состоит. На третьем шаге корректируем выбранные
примитивы, с целью приведения их к гладкому виду. На четвертом этапе,
методом динамического программирования, отбираем только необходимые для
построения следа примитивы, по которым строим окончательный вариант
кривой. На пятом, заключительном этапе, пересчитываем полученную
траекторию в физические единицы измерения.
Проиллюстрируем представленный выше рисунок фрагментами изображения и кратко поясним, что происходит на каждом из этапов.
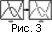
Исходный материал существует в виде изображений на бумаге или микрофильмов. Для ввода этих изображений с бумажного носителя используется планшетный сканер. В случае микрофильмов может использоваться либо проекционный сканер, либо цифровой фотоаппарат с большой разрешающей способностью. Результаты сканирования могут сохраняться в виде изображения (например, в графическом формате TIFF, см. [Борн, 1995]) как двухцветного (черно-белого), так и содержащего оттенки серого или цветного. Если исходное изображение не является двухцветным, то оно приводится к нему путем порогового преобразования. В результате получается двухцветное изображение, где 0 соответствует фону, а 1 - сигналу. При необходимости осуществляется ориентация изображения (поворот и отражение) так, чтобы временная ось была горизонтальной, запись разворачивалась слева направо, ось величины сигнала была направлена снизу вверх.
Рассмотрим подробнее способ перевода изображения к двухцветному представлению. Если изображение цветное, каждая точка может быть задана тройкой чисел (R,G,B), определяющей, каким образом данный цвет получается из трех основных цветов: красного (R), зеленого (G) и синего (B). Каждая из этих величин принимает целые значения и находится в пределах от 0 до 255.
С учетом интенсивности цветное изображение преобразуется в оттенки серого по следующей формуле:
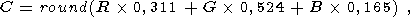 | (1) |
где C - может принимать целые значения от 0 до 255, 0 соответствует черному цвету, 255 - белому, а все остальные значения - промежуточным оттенкам серого.
После преобразования цветного изображения в многоуровневое черно-белое необходимый порог для перехода к двухцветному представлению выбираем на основе минимизации суммы дисперсий частей гистограммы слева и справа от него.
Теперь, когда изображение приведено к двухцветному представлению, осталось определить: какой из этих двух цветов соответствует сигналу, а какой - фону. Для этого вычисляем процент площади, покрываемой каждым из этих цветов, и фоновым объявляем цвет, получивший больший процент (более 50%). Данные о занимаемой площади могут быть получены как путем анализа самого изображения (в том числе методом Монте-Карло [Бахвалов, 1975; Бахвалов и др., 1987]), так и его гистограммы.
Математическая морфология (mathematical morphology) - это теория, изучающая методы выделения структурной информации на изображении для ее использования в машинном зрении (computer vision). Изображения в ней рассматриваются как функции на целочисленной решетке. В связи с этим математическую морфологию можно рассматривать как формальный язык с элементарными операторами и операциями (sup, inf, композиция), областью действия которых являются подмножества этой решетки.
Определение 2.1-1.
Множество
L называем частично упорядоченным, если на
нем введена операция отношения
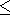 такая, что для любых
a,b,c
такая, что для любых
a,b,c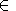 L выполнены
три свойства:
L выполнены
три свойства:
1) рефлективность:
a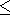 a
a
2) антисимметричность: если
a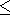 b, то
-b
b, то
-b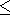 -a
-a
3) транзитивность: если
a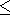 b и
b
b и
b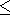 с, то
a
с, то
a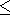 c.
c.
Определение 2.1-2. Полной решеткой (complete lattice) называем частично упорядоченное множество, любое непустое подмножество которого имеет точную верхнюю и нижнюю грани.
Определение 2.1-3. Математическая морфология - это теория, изучающая распределение операторов между полными решетками в терминах некоторого семейства простых операторов: расширение (dilation), размывание (erosion), анти-расширение (anti-dilation), анти-размывание (anti-erosion). Эти операторы называют элементарными операторами математической морфологии.
Операторы языка строятся из элементарных путем их объединения, пересечения и композиции. Построенные операторы могут использоваться как основные для построения других операторов и т.д. Множество этих операторов и операций образуют " набор инструментов математической морфологии" (НИММ). С практической точки зрения, НИММ является набором инструментов для выделения структурной информации на изображения в задачах машинного зрения.
Операторы в НИММ организуются иерархически, основываясь на их распределении в терминах элементарных операторов. Таким образом, мы определяем, в порядке возрастания сложности, следующие семейства операторов и операций: основные операторы и операции, операторы первого, второго и третьего уровня. Здесь будут определены операторы, необходимые для решаемой задачи. Описание других можно найти в работах по математической морфологии [Banon and Barrera, 1991; Konstantinides and Rasure, 1994].
С алгебраической точки зрения элементарные операторы являются отображениями между полными решетками со следующими свойствами:
Определение 2.1-4. Пусть
L1 и
L2 - полные решетки,
c L1.
Оператор
y называется
L1.
Оператор
y называется
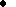 расширением из
L1 в
L2, если
y(
расширением из
L1 в
L2, если
y(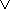 c)=
c)=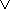 y(c)
y(c)
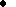 размыванием из
L1 в
L2, если
y(
размыванием из
L1 в
L2, если
y(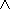 c)=
c)=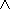 y(c)
y(c)
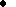 анти-расширением из
L1 в
L2, если
y(
анти-расширением из
L1 в
L2, если
y(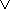 c)=
c)=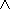 y(c)
y(c)
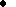 анти-размыванием из
L1 в
L2, если
y(
анти-размыванием из
L1 в
L2, если
y(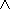 c)=
c)=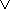 y(c),
y(c),
где
 и
и
 означают соответственно пересечение и объединение
в
теоретико-множественном смысле.
означают соответственно пересечение и объединение
в
теоретико-множественном смысле.
Пусть Z - множество целых чисел,
I={-1,0,1} {-1,0,1}
{-1,0,1} Z2,
E=([0,m]
Z2,
E=([0,m] [0,n])
[0,n])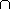 Z2,
K=[0,k]
Z2,
K=[0,k]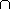 Z, где
k,m,n>0.
Обозначим
KE - множество функций из
E в
K. Далее, если не указано
противное, мы полагаем что
f, g, f1, f2 - функции из
KE. Эти функции
представляют изображение с оттенками серого и бинарное, если
K={0,1}.
Z, где
k,m,n>0.
Обозначим
KE - множество функций из
E в
K. Далее, если не указано
противное, мы полагаем что
f, g, f1, f2 - функции из
KE. Эти функции
представляют изображение с оттенками серого и бинарное, если
K={0,1}.
Пересечение и объединение двух функций определяется соответственно следующими формулами:
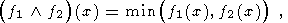 | (2) |
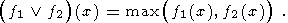 | (3) |
Операторы дополнения и разности определим соответственно как
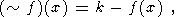 | (4) |
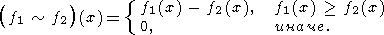 | (5) |
Пусть B, h - вектор из Z2. Тогда обозначим
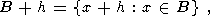 | (6) |
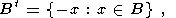 | (7) |
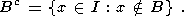 | (8) |
Определение 2.1-5. Структурным элементом называем
любое подмножество
B. Множество
I называем элементарным квадратом. В дальнейшем мы
будем задавать структурные элементы в виде матрицы размера
3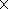 3, где
единицы соответствуют присутствию данного элемента в
B, а ноль - его
отсутствию.
3, где
единицы соответствуют присутствию данного элемента в
B, а ноль - его
отсутствию.
Введем две бинарные операции из
K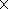 Z в
K, определенные для всех
t
Z в
K, определенные для всех
t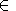 K, n:
K, n:
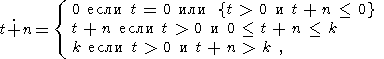 | (9) |
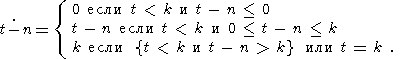 | (10) |
Определение 2.1-6. Пусть g - функция, отображающая структурный элемент B в Z, fE - функция из E в K. Тогда расширением (соответственно размыванием) функции f по g называется функция dg(f)E (соответственно eg(f)E ), определенная для любого x и задаваемая как
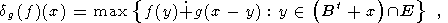 | (11) |
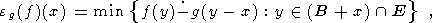 | (12) |
причем
max(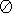 )=0, min(
)=0, min(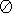 )=k.
)=k.
Далее мы будем использовать частный случай этого определения - когда функция g постоянна и равна нулю. При этом расширение и размывание зависят только от структурного элемента B и называются соответственно расширением и размыванием f по B. Формулы для них перепишутся в виде:
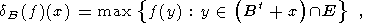 | (13) |
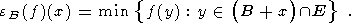 | (14) |
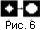
 На рисунках (рис. 6, рис. 7) показано изображение до и после
применения расширения и размывания при использовании в качестве
структурного элемента квадрат
I={-1,0,1}
На рисунках (рис. 6, рис. 7) показано изображение до и после
применения расширения и размывания при использовании в качестве
структурного элемента квадрат
I={-1,0,1} {-1,0,1}.
{-1,0,1}.
Следует отметить, что операторы расширения и размывания, вообще говоря, не являются обратными друг к другу. Их композиция образует либо оператор открытия, либо замыкания (в зависимости от их положения в ней), которые будут рассмотрены ниже.
Определение 2.1-7. Оператор i из KE в KE, заданный для любого f, такой что
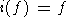 | (15) |
назовем единичным оператором.
Эти операторы строятся с использование только одного основного оператора каждого типа. Определим некоторые из них
Определение 2.1-8. Операторы
 | (16) |
назовем соответственно анти-расширением и анти-размыванием по B.
Определение 2.1-9. Операторы
 | (17) |
назовем соответственно открытием и замыканием по B.
Используя в качестве структурного элемента квадрат
I={-1,0,1}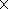 {-1,0,1},
изобразим результат применения к изображению (рис. 8б) оператора
открытия (рис. 8а) или замыкания (рис. 8в).
{-1,0,1},
изобразим результат применения к изображению (рис. 8б) оператора
открытия (рис. 8а) или замыкания (рис. 8в).
Определение 2.1-10. Пусть
A и
B - структурные элементы,
и
A B. Тогда операторы
B. Тогда операторы
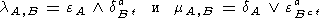 | (18) |
назовем соответственно порождающим сверху и порождающим снизу.
Определение 2.1-11. Операторы
 | (19) |
назовем соответственно операторами уменьшения и увеличения толщины по паре структурных элементов (A,B).
Эти операторы строятся с использованием конечного числа основных операторов. Введем следующие обозначения:
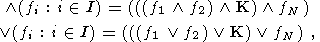 | (20) |
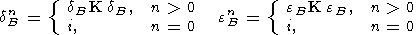 | (21) |
n-кратное расширение и n-кратное размывание,
 | (22) |
n-кратное открытие и n-кратное замыкание по B.
Пусть a и b - две конечные последовательности, состоящие из n структурных элементов, причем Aii. Тогда
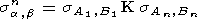 | (23) |
n-кратное уменьшение толщины по паре (a,b).
Эти операторы строятся рекурсивно, используя изначально неопределенное число основных операторов. Далее мы используем лишь один из этих операторов.
Определение 2.1-12. Пусть a и b - две бесконечные последовательности структурных элементов Ai и Bi, причем Aii. Тогда оператором построения скелета путем уменьшения толщины по паре (a, b) назовем композицию
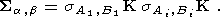 | (24) |
Для примера рассмотрим следующую последовательность структурных элементов:
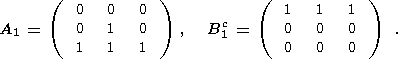 | (25) |
Остальные структурные элементы строим так: последующий получаются из предыдущего его поворотом по часовой стрелке на 45 градусов. Таким образом
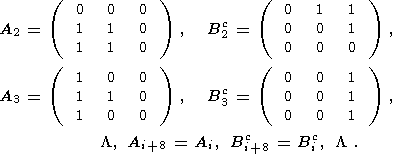 | (26) |
 Скелет изображения, построенного с помощью оператора, определяемого
формулой (24) и использующего последовательности структурных
элементов (25) и (26) изображен на рис. 9.
Скелет изображения, построенного с помощью оператора, определяемого
формулой (24) и использующего последовательности структурных
элементов (25) и (26) изображен на рис. 9.
Замыкание информационных областей на изображении применяется, чтобы сгладить ребристость границ областей сигнала для более точного построения скелета.
Замыкание представляет собой совокупность двух последовательно
примененных операций (вначале расширение, затем размывание) и
определяется по формуле (17). Для построения замыкания, в качестве
структурного элемента
B мы используем элементарный квадрат
I={-1,0,1} {-1,0,1}. Отметим два очевидных
свойства:
{-1,0,1}. Отметим два очевидных
свойства:
Утверждение 2.2-1. При замыкании происходит объединение информационных "островков" на изображении, расстояние между которыми меньше размера структурного элемента.
Утверждение 2.2-2. При замыкании фоновые "дырки" на изображении, которые меньше, чем структурный элемент, закрываются.
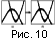 В результате проведения замыкания получаем более однородное,
т.е. с
меньшей ребристостью на краях информационных областей, изображение
(рис. 10).
В результате проведения замыкания получаем более однородное,
т.е. с
меньшей ребристостью на краях информационных областей, изображение
(рис. 10).
Построение скелета информационных областей происходит путем уменьшения их толщины и так, чтобы при этом не образовывались разрывы. При этом образуется семейство цепочек (дискетный аналог однопараметрических кривых), которое определяет направление вытянутости области в окрестности точек каждой цепочки (рис. 2б). Преобразование изображения осуществляется с помощью модификации формулы (24):
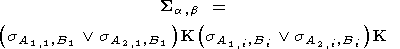 | (27) |
где используется следующие последовательности структурных элементов:
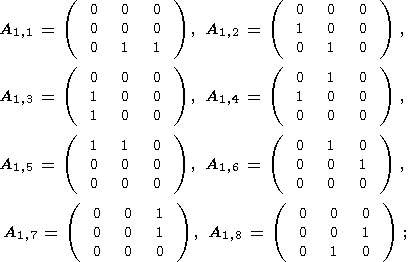 | (28) |
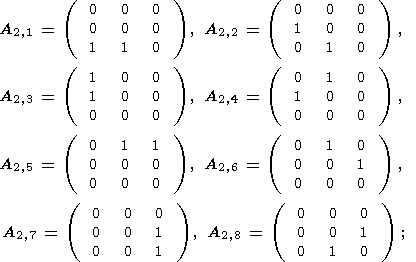 | (29) |
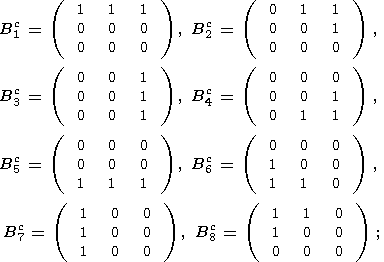 | (30) |
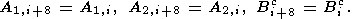 | (31) |
Определение 2.4-1. Ближайшей окрестностью точки ai,j называем множество точек bm,n таких, что max(|i-m|, |j-n|)=1.
Просматривая все изображение, после построения его скелета, мы удаляем точки, содержащие в ближайшей окрестности более двух точек. В результате получаем множество кривых, никакие две из которых не пересекаются (рис. 2в). Далее эти кривые будем называть примитивами или сегментами.
Исходные данные - это двухуровневое изображение, где 0 соответствует фону, а 1 - сигналу. Мы хотим перейти к его многоуровневому представлению, где точкам информационных областей соответствуют тем большие значения, чем сильнее они удалены от краев области, к которой сами принадлежат. Тем самым, точкам, находящимся в центре информационных областей, будут соответствовать наибольшие значения.
Алгоритм 3.1-1. Переход от двухуровневого изображения к трехмерному представлению.
Алгоритм состоит из прямого и обратного прохода по изображению:
Прямой проход: Отождествляя изображение с матрицей размера
M N, мы
индуктивно просматриваем матрицу (изображение), начиная с ее верхнего
левого угла и заканчивая правым нижним, изменяя значения ненулевых
элементов по формуле:
N, мы
индуктивно просматриваем матрицу (изображение), начиная с ее верхнего
левого угла и заканчивая правым нижним, изменяя значения ненулевых
элементов по формуле:
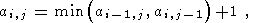 | (32) |
где i = 1..M-2, j = 1..N-2, ai,j>0.
Обратный проход: Индуктивно просматриваем матрицу, начиная с ее правого нижнего угла и заканчивая левым верхним, изменяя значения ненулевых элементов по формуле:
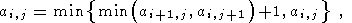 | (33) |
где i = 1..M-2, j = 1..N-2, ai,j>0.
Если ai,j=0, то для такого элемента значение по формулам (32), (33) не вычисляется.
Нетрудно видеть, что после этих преобразований изображение будет иметь искомый вид.
Возможны другие варианты индуктивного перехода к многоуровневому изображению (например, не по двум, а по трем или пяти направлениям). Однако метод построения хребта тесно связан с нахождением по нему скелета, поэтому данные задачи следует рассматривать только совместно. Ниже будет представлен алгоритм нахождения скелета по центральному хребту, построенному указанным способом.
Итак, мы выделили центральные хребты информационных областей изображения и теперь хотим построить по ним его структурный скелет. Прежде всего заметим, что любой ненулевой элемент матрицы имеет соседом элемент на единицу меньший его, по крайней мере, по одному из четырех основных направлений (влево, вправо, вверх, вниз). Также, возможно, он имеет среди соседей элемент на единицу больший его.
Введем общее определение точек хребта:
Определение 3.2-1. Точками хребта будем называть те точки целочисленной решетки, в которых хотя бы одна из частных производных (по x или y ) меняет знак, и точка является локальным максимумом по этому направлению.
С учетом специфики дискретного случая, а также используемого метода построения хребта, формальное условие на точки хребта будет выглядеть так:
Определение 3.2-2. Точка ai,j0 на изображении является точкой хребта, если она является локальным, причем выполнено хотя бы одно из следующих четырех условий:
1) ai,j > ai,j-1 и ai,j > ai,j+1,
2) ai,j = ai,j-1, ai,j > ai,j-2 и ai,j > ai,j+1,
3) ai,j > ai-1,j и ai,j > ai+1,j,
4) ai,j = ai-1,j, ai,j > ai-2,j и ai,j > ai+1,j.
Второе и четвертое условие связано с тем, что хребет (в силу своего построения) может иметь ширину не в одну, а в две точки. В этом случае из них оставляем только одну (поэтому условий четыре, а не шесть).
Совокупность всех точек хребта образует предварительный скелет изображения. Точки хребта ищутся за один просмотр изображения в соответствии с определением 2.3-2. После этого изображение преобразуется к трехуровневому виду: 0 - фон, 1 - информационные области, кроме точек хребта, 2 - точки хребта.
Построенный на предыдущем этапе скелет нельзя сразу использовать для выделения примитивов, поскольку он содержит узловые точки, а также может иметь разрывы на участках с сильной изрезанностью информационных областей, где построение скелета указанным выше методом может приводить к ошибочному исключению или добавлению точек. В связи с этим мы проводим трехшаговую коррекцию предварительного скелета.
На первом шаге удаляем угловые точки.
Определение 3.3-1. Точку ai,j=2 (точка хребта) на изображении называем угловой точкой, если выполнено хотя бы одно из следующих четырех условий:
1) ai+1,j = ai,j+1 = 2,
2) ai-1,j = ai,j+1 = 2,
3) ai+1,j = ai,j-1 = 2,
4) ai-1,j = ai,j-1 = 2.
Угловые точки ищутся и удаляются индуктивно за один просмотр изображения в соответствии с определением 3.3-1.
На втором шаге пытаемся соединить небольшие разрывы.
Определение 3.3-2. Ближайшей окрестностью точки ai,j называем множество точек bm,n таких, что max(|i-m|, |j-n|)=1.
Определение 3.3-3. Точка bm,n касается точки ai,j, если она лежит в ближайшей окрестности точки ai,j.
Определение 3.3-4. Точку ai,j=1 (точка информационной области, но не хребта) на изображении называем точкой восстановимого разрыва, если выполнено два условия:
1) в ее ближайшей окрестности присутствуют ровно две точки хребта;
2) эти две точки не касаются друг друга.
Точки восстановимого разрыва ищутся и удаляются индуктивно за один просмотр изображения в соответствии с определением 3.3-4.
На третьем шаге мы удаляем узловые точки.
Определение 3.3-5. Точку ai,j=2 (точка хребта) на изображении называем узловой точкой, если в ее ближайшей окрестности лежит не менее трех точек.
Узловые точки ищутся и удаляются индуктивно за один просмотр изображения в соответствии с определением 3.3-5.
В результате мы получили множество цепочек, никакие две из которых не пересекаются. Теперь структурный скелет изображения определяется набором элементарных примитивов.
Этот шаг разбивается на четыре этапа. Во-первых, мы представляем примитивы в виде последовательности точек так, что следующий элемент последовательности лежит в окрестности предыдущего элемента. Во-вторых, проводим предварительное сглаживание сегмента. В-третьих, мы разбиваем сегмент на несколько частей (новых сегментов) так, чтобы x(t) была бы монотонна. В-четвертых, удаляем последовательные точки в каждой из частей, имеющие одинаковую абсциссу с тем, чтобы иметь возможность представлять полученные части в виде функций y(x).
Итак, на первом этапе мы хотим представить сегмент как вектор-функцию, заданную для целых значений аргумента:
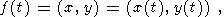 | (34) |
где t=0..N-1; N - число точек в сегменте.
Для этого мы просматриваем изображение, извлекаем связанные (по определению касания 3.3-3) участки скелета, образующие сегменты, и преобразуем их к виду (34). При этом f(0) соответствует начальной точке сегмента, а f(N-1) - конечной.
На втором этапе мы сглаживаем x(t), компенсируя ее колебания не превышающие вариации 1. Т.е. значения функции x(t) на участке, где разница между максимумом и минимумом не превышают 1, устанавливаем равными ее округленному среднему значению на этом участке.
На третьем этапе мы ищем точки, в которых производная от функции x(t) меняет знак, и разбиваем сегмент на части в этих точках. Производная вычисляется по методу разделенных разностей ([Бахвалов, 1975; Бахвалов и др., 1987]) по следующей формуле:
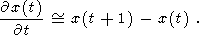 | (35) |
На четвертом этапе удаляем последовательные точки, имеющие одинаковую абсциссу, получая либо вертикальный сегмент (состоящий из двух точек с одинаковой абсциссой), либо регулярный сегмент (который может быть параметризован как y(x) ).
В результате имеем набор примитивов, которые могут быть представлены как y(x) и использоваться для интерполяции сплайнами в дальнейшем (в вертикальных сегментах используется лишь одна из точек). Каждый примитив характеризуется своими точками, минимальным квадратом, в который он может быть вписан, а также флагом, показывающим является ли он строго вертикальным или нет.
Здесь мы рассмотрим преимущества и недостатки методов построения скелета с использованием преобразования расстояний и рассмотренной в предыдущей главе математической морфологии.
Основным недостатком техники математической морфологии по сравнению с методом преобразования расстояний является скорость. Операторы математической морфологии "снимают шкурку" с информационных областей, уменьшая их толщину по всем или только по выбранным направлениям в зависимости от используемого набора структурных элементов. Это приводит к весьма аккуратному (при правильном выборе структурных элементов) скелету, однако требует многократного просмотра изображения: не менее 1/2 от минимальной ширины наиболее широкой области. С учетом того, что для нахождения скелета обычно используется последовательность структурных элементов, это число возрастает в несколько раз. Например, в случае использования последовательности элементов заданной формулами (25) и (26) для изображения с шириной областей в 10 точек (что очень немного), изображение придется просматривать около 20 раз. Для построения достаточно качественного скелета (аналогичного тому, что строится математической морфологией) методу преобразования расстояний требуется лишь трехкратный просмотр изображения, причем независимо от размеров информационных областей на нем.
В результате обоих методов получается приблизительно одинаковый и достаточно качественный скелет, что делает их сравнимыми по этому показателю.
Оба метода могут применяться к многоуровневым изображениям в оттенках серого.
Оба метода достаточно гибкие, но математическая морфология обладает более широким спектром возможностей за счет богатого выбора структурных элементов. При использовании метода преобразования расстояний некоторая свобода достигается благодаря различным вариантам построения "центрального хребта" и способам нахождения его вершины.
Таким образом, при построении скелета метод преобразования расстояний в целом более эффективен по сравнению с математической морфологией, однако методы математической морфологии тоже могут эффективно применяться при небольшой ширине информационных областей.
В основе реконструкции следа самописца лежит выбор последовательности сегментов, определяющих оптимальный путь. Это осуществляется методом динамического программирования с условием минимизации суммы локальных весов склейки сегментов. Пример нахождения такого пути представлен на рис. 4. Локальные веса склейки определяются, исходя из двух факторов: расстояние между сегментами и сонаправленности их ближайших концевых участков.
Величина веса склейки сегментов зависит, во-первых, от расстояния между их концевыми точками, и, во-вторых, от величины углов между прямой, соединяющей рассматриваемые концевые точки, и касательными к сегментам в этих точках. Точки, являющиеся началом и концом участка, на котором строится оптимальный путь, будем называть граничными.
Если вычисляется вес между примитивом и граничной точкой, то для нахождения веса используются все точки сегмента и учитывается угол между касательной в рассматриваемой точке и прямой соединяющей ее с граничной точкой. Вес между граничными точками определяется только по расстоянию между ними.
Запишем сказанное выше в виде формул. Пусть имеются два сегмента
A={a1, ,
am},
B={b1,
,
am},
B={b1, ,
bn} и
две точки
p, q, где
ai, bi,
p, q
,
bn} и
две точки
p, q, где
ai, bi,
p, q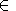 R2.
Рассмотрим,
как вычисляются для них значения весовой функции.
R2.
Рассмотрим,
как вычисляются для них значения весовой функции.
Пусть нужно вычислить вес склейки сегментов A и B. Он равен минимальному из четырех весов склейки концов сегментов. Для определенности рассмотрим начало сегмента A и начало сегмента B (остальные три вычисляются аналогично).
В начале, методом разделенных разностей вычисляем производные на концах и определяем их угол наклона (тангенс угла наклона равен значению производной).
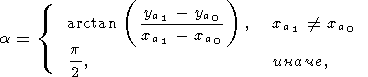 | (36) |
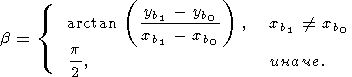 | (37) |
Определим угол наклона прямой, соединяющей начальные точки сегментов:
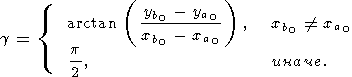 | (38) |
Найдем средний угол отклонения касательных в начальных точках сегментов от прямой, соединяющей эти точки, и нормируем его, т.ч. максимальное значение равно 1:
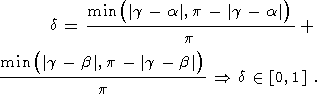 | (39) |
Искомое расстояние D(A, B) вычисляется по следующей формуле:
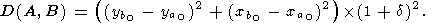 | (40) |
Таким образом, искомое расстояние будет возрастать при удалении сегментов друг от друга и увеличении углов между прямой, соединяющей рассматриваемые концевые точки сегментов, и касательными к ним в этих точках.
Рассмотрим теперь, как вычисляется расстояние между сегментом A и граничной точкой p. Для этого находим минимум среди расстояний между всеми точками сегмента и граничной точкой.
 При вычислении этих расстояний подобно предыдущему используется
угол между касательной к сегменту в рассматриваемой точке и прямой,
соединяющей эту точку с граничной точкой. На концах угол определяется
как на рис. 11,
а на внутренних точках по следующей формуле:
При вычислении этих расстояний подобно предыдущему используется
угол между касательной к сегменту в рассматриваемой точке и прямой,
соединяющей эту точку с граничной точкой. На концах угол определяется
как на рис. 11,
а на внутренних точках по следующей формуле:
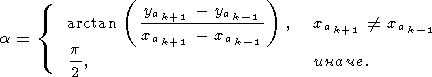 | (41) |
Нормированный угол отклонения касательных в точках сегмента от прямой, соединяющей эти точки, определяется как:
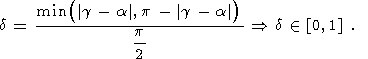 | (42) |
Искомое расстояние D(A, p) будет вычисляться по формуле:
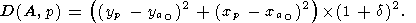 | (43) |
Расстояние между граничными точками p и q D(p, q) будет вычисляться по формуле:
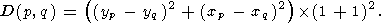 | (44) |
В качестве базовой предпосылки отбора сегментов предполагается, что вероятность последовательного соединения двух примитивов в искомом следе обратно пропорциональна некой весовой функции, зависящей только от этих двух примитивов. Исходя из этого, можно считать, что сумма весовых функций последовательно соединенных сегментов, образующих оптимальный путь, будет минимальна:
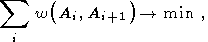 | (45) |
где Ai - i ый сегмент в последовательности примитивов определяющих след, а w(Ai, Ai+1) - значение весовой функции.
Представим скелет изображения, полученный на предыдущем этапе, как
ориентированный граф, содержащий циклы и петли. Вершины в графе - это
примитивы (сегменты) изображения, а также две точки, между которыми
должен быть восстановлен след. Каждому ребру в графе приписано число - вес
(стоимость локальной склейки сегментов). В графе выделены две вершины
(указанные выше ограничивающие точки), одну из них называем началом, а
другую - концом пути. Требуется найти путь из начальной вершины в конечную
так, чтобы сумма весов была минимальной. Для этой цели мы используем
модификацию алгоритма
A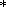 , подробно рассмотренного
в
[Spouge, 1989].
, подробно рассмотренного
в
[Spouge, 1989].
 В начале кратко поясним суть алгоритма (рис. 12).
В начале кратко поясним суть алгоритма (рис. 12).
Изначально все вершины, кроме начальной, полагаем открытыми. На
каждом шаге ищем открытую вершину с номером
k, выбранный путь до
которой имеет минимальную (среди других вершин) длину
sk, и полагаем ее
закрытой. Рассмотрим открытые вершины с номерами
i и путями
si, в которые
входит ребро веса
wki из вершины
k. Тогда, если
sk+wki
Теперь рассмотрим этот алгоритм более подробно. Пусть граф содержит
N+1 вершину. Каждому ребру
(i,j) приписан вес, задаваемый как
cost(i,j).
Начальную вершину исключаем из рассмотрения, и остается
N вершин. Введем
три вектора размера
N, называемые chain, flags, costs:
Алгоритм 4.2-1. Отбор примитивов, образующих оптимальный
путь.
Алгоритм состоит из трех этапов:
1. Инициализация - все вершины открыты, никакие цепочки не
определены,
вектор стоимости содержит веса ребер соединяющих начальную вершину со
всеми остальными
2. Прямой проход (поиск оптимального пути)
3. Обратный проход (восстановление пути) - после завершения
работы второй части, по вектору chain, начиная с конечной вершины, восстанавливаем
оптимальный путь.
Сформулируем и докажем несколько утверждений, на которых
основывается алгоритм.
Утверждение 4.2-1. Алгоритм требует не более
N2/2 вычислений весов между
вершинами (функция cost( i,j )). Тем самым не требуется хранить матрицу весов.
Число арифметических операций порядка
N2.
Доказательство: очевидно из структуры алгоритма
4.2-1, поскольку после
каждого шага число открытых вершин уменьшается на 1.
Определение 4.2-2. Будем называть сумму весов ребер, образующих
путь до
вершины, весом пути до этой вершины.
Определение 4.2-3. Путь до вершины назовем минимальным,
если он имеет
наименьший вес среди всех ведущих в нее путей.
Определение 4.2-4. Открытую вершину, выбранный путь до которой
в данный
момент обладаем наименьшим весом (среди путей в этот же момент ведущих к
другим вершинам), назовем оптимальной стартовой вершиной.
Определение 4.2-5. Шагом алгоритма из выбранной вершины
будем называть
последовательность действий, заданных циклом FOR в части 2, алгоритма 4.2-1.
Утверждение 4.2-6. Путь до оптимальной стартовой вершины
является
минимальным.
Доказательство: очевидно, в силу определения оптимальной
стартовой
вершины: прохождение пути через любую из оставшихся вершин, приведет
лишь к увеличению веса пути до стартовой вершины.
Следствие 4.2-6-1. Шаг из оптимальной стартовой вершины
может быть
произведен лишь однажды, поэтому сразу после этого такую вершину можно
положить закрытой и далее не рассматривать.
Доказательство: очевидно, в силу минимальности пути до нее.
Следствие 4.2-6-2. Полученный в результате алгоритма 4.2-1
путь в графе
является минимальным.
Доказательство: В силу утверждения 4.2-6, путь
до каждой из вершин,
определяющих по завершению алгоритма путь в графе, является минимальным.
Поэтому до конечной точки будет также минимальным.
Следствие 4.2-6-2 доказывает, что представленный выше алгоритм 4.2-1
выбора примитивов, образующих оптимальный путь, действительно
минимизирует сумму локальных весов склейки сегментов.
Напомним определение кубического интерполяционного сплайна и
выпишем формулы для его построения (более подробно об этом и других
способах интерполяции сплайнами см.
[Бахвалов, 1975;
Бахвалов и др., 1987]).
Определение 4.3-1. Пусть заданы
N +1 точка:
x0,
Введем обозначение
Тогда при
x
Дважды интегрируя это равенство, константы находим из условий:
1.
S(xi)=f(xi),
i=0..N,
2.
S(x) - дважды непрерывно дифференцируема на [x0, xN ].
В результате имеем при
x
Надо найти вектор
M=(M0,
Отсюда, полагая
M0=MN=0,
i=1..N-1 получаем систему из
N-1 уравнения:
с
N-1 неизвестным:
В матричном виде (50) можно записать
CM
Выпишем основные формулы для решения уравнений с трехдиагоальной
матрицей методом прогонки. Пусть имеется система уравнений:
Выражая из
k -ого уравнения
xk получаем:
где
Для решения системы сначала вычисляем значения
Ak и
Bk, начиная с 1, затем
находим
xk, начиная с последнего. Первое требует
3N арифметических
операций, второе -
5N.
Теперь, когда найдены все коэффициенты, можем определить
f(x) для
любого
x на рассматриваемом отрезке.
Окончательный вариант кривой строится в три этапа:
По полученным в результате интерполяции узлам мы можем
восстановить значения амплитуды в каждый момент времени, т.е. определить
последовательность значений при любой дискретизации по времени. Зная
соотношение между единицами измерения на изображении и физическими
единицами, полученные результаты сводятся к физическим единицам
изменения линейным преобразованием.
Класс CSrcImage отвечает за загрузку изображения, пороговые
преобразования с целью приведения его к двухцветному представлению,
геометрические преобразования (поворот, отражение и т.д.), и начало
построения скелета (до его описания в терминах примитивов).
Класс CSeg - содержит описание отдельного сегмента (примитива):
концевые точки, набор образующих точек, координаты минимального
описанного прямоугольника.
Класс CImageSkeleton содержит описание скелета в виде набора
примитивов и методы приведения последних к регулярному виду.
Класс CImageTrace отвечает за построение искомой траектории, на
основе данных из класса CImageSkeleton.
Класс CUnitedTrace позволяет работать одновременно с несколькими
независимыми фрагментами траектории (объектами класса CImageTrace). Он
также осуществляет запись результатов в нужном формате.
Классы CBaseline, CTimeMarks и CAmplitudeMarks, содержат
информацию и методы соответственно для определения базовой линии,
временных меток и амплитудной привязки.
По завершении предварительного этапа дается команда на построение
скелета всего изображения. Результат представлен на рис. 16.
После того как траектория найдена, устанавливаются отметки
для
сведения результатов к физическим единицам, используя соответствующие
команды панели инструментов (рис. 17).
На последнем этапе задается связь между единицами на изображении и
физическими значениями, а также выбирается формат записи результатов в
файл.
Рассмотренный алгоритм позволяет решать весь спектр задач по
оцифровке сигналов, в которых временная ось не меняет направление. Это
могут как геофизические записи, так и любые другие, которые представляют
собой последовательность отклонений от некоторой нулевой базовой линии
(колебания маятника, звуковые колебания, след автомобиля на прямом участке
дороги). При незначительном изменении в процедуру выборки необходимых
сегментов (снятие условия, что последующий сегмент имеет большую
временную координату, чем предыдущий), а также использовании других
методов интерполяции для построения результирующей кривой, алгоритм
может применяться, например, для оцифровки объектов (границ регионов, рек,
морей и т.п.) на географических картах.
Эффективность алгоритма зависит в первую очередь от качества
исходного изображения: он более эффективен на изображении с четко
определенными областями полезного сигнала и малым количеством шума (в
том числе, пересечений близлежащих участков траекторий).
Кроме этого,
значительную роль в удобстве и скорости работы играет его программная
реализация и производительность компьютера, на котором это приложение
будет использоваться. Наиболее подходящим языком программирования для
решения как вычислительных, так и интерфейсных задач является C++, на
котором этот алгоритм и был реализован.
При оцифровке изображений с высоким уровнем шума граничные точки
располагаются на меньшем расстоянии, что позволяет снизить вероятность
ошибки. Однако даже в самых сложных случаях, когда приходится двигаться
шагами, захватывающими лишь один узел (точку пересечения с другой
траекторией), требуется значительно меньше усилий, чем в случае стандартного
метода оцифровки на дигитайзере или с помощью мыши на дисплее
компьютера. Компьютер делает всю черновую работу и оператору остается
лишь корректировать его деятельность при ошибочном выборе направления в
узловых точках.
Бахвалов Н. С., Численные методы, Наука, Москва, 1975.
Бахвалов Н. С., Жидков, Кобельков Г. М., Численные методы, Наука,
Москва, 1987.
Борн Г., Форматы данных, Торгово-издательское бюро BHV, Киев, 1995.
Минул М., Математическое программирование, теория и алгоритмы, Наука, Москва,
1990.
Фаулер М, Скотт К., UML в кратком изложении, Мир, Москва, 1999.
Banon G. J. F., and Barrera J., Minimal representation for translation
invariant set mapping by mathematical morphology, SIAM Journal of Applied Mathematics,
51, (6), 1782-1798, December 1991.
Bellman R.E., Dynamic programming, Princeton University Press, Princeton,
NJ,
1957.
Konstantinides K., and Rasure J. R., The Khoros Software Development
Environment for Image and Signal Processing, IEEE Transaction on image processing,
3, (3), 243-252, May 1994.
John L. Spouge, Speeding up dynamic programming algorithms for finding
optimal lattice path, SIAM Journal of Applied Mathematics, 49, (5),
1552-1566, October 1989.
Paul L. Rosin, Geoff A.W. West, Salience distance transforms, Graphical Models
and Image Processing, 57, (6), 483-521, 1995.
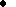 сhain[i] - содержит номер вершины, предшествующей
вершине с номером
i,
в наилучшем (в данный момент) пути из начальной точки в
i -ую вершину
сhain[i] - содержит номер вершины, предшествующей
вершине с номером
i,
в наилучшем (в данный момент) пути из начальной точки в
i -ую вершину
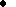 costs[i] - содержит стоимость (т.е. сумму
весов) наилучшего (в данный
момент) пути из начальной точки в
i-ую вершину
costs[i] - содержит стоимость (т.е. сумму
весов) наилучшего (в данный
момент) пути из начальной точки в
i-ую вершину
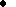 flags[i] - показывает, можем ли мы делать
шаг из данной вершины (если да,
то вершину назовем открытой, иначе - закрытой)
flags[i] - показывает, можем ли мы делать
шаг из данной вершины (если да,
то вершину назовем открытой, иначе - закрытой)
FOR (каждая вершина i ) DO
chain[i]="не определена"
flags[i]="открыта"
costs[i]=cost("начальная вершина", i )
ENDFOR
WHILE (существует открытая вершина) DO
k= arg( min(costs[i] : flags[i] == "открыта"))
flags[k] ="закрыта"
IF ( k == конечная вершина)
завершить цикл
ENDIF
FOR (каждая вершина j, такая что существует
ребро ( k,j )) DO
IF (flags[j] == "открыта"
AND costs[j] > costs[k] + cost(k,j) )
costs[j]= costs[k] + cost(k,j)
chain[j]=k
ENDIF
ENDFOR
ENDWHILE
k ="конечная вершина"
path="пустой"
WHILE (chain[k] - определена) DO
k =chain[k]
вставить k в начало path
ENDWHILE




4.3. Интерполяция кубическими сплайнами
 , xN
(N
, xN
(N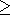 2).
Кубическим интерполяционным сплайном
S(x) функции
f по этим точкам называется
кусочно-полиномиальная функция третьей степени, обладающая непрерывными
производными второго порядка в точках
x0,
2).
Кубическим интерполяционным сплайном
S(x) функции
f по этим точкам называется
кусочно-полиномиальная функция третьей степени, обладающая непрерывными
производными второго порядка в точках
x0, , xN
такая, что
S(xi)=f(xi),
i=0..N.
, xN
такая, что
S(xi)=f(xi),
i=0..N. 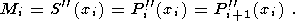
(46) 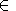 [xi-1,
xi]
[xi-1,
xi] 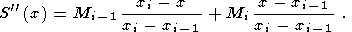
(47) 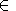 [xi-1,
xi],
hi=xi-xi-1,
i=1..N
[xi-1,
xi],
hi=xi-xi-1,
i=1..N 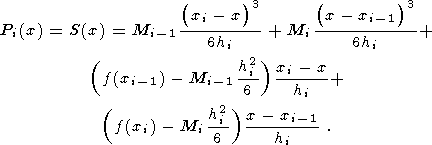
(48)  ,
MN). В силу второго условия
,
MN). В силу второго условия
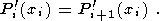
(49) 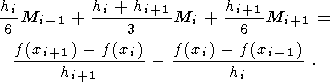
(50) 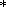 = d, где
C - трехдиагональная матрица размера
N-1
= d, где
C - трехдиагональная матрица размера
N-1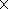 N-1,
M
N-1,
M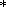 =(M1,
=(M1, , MN-1),
d - вектор-столбец высоты
N-1. Данная система решается методом прогонки за
8N арифметических операций.
, MN-1),
d - вектор-столбец высоты
N-1. Данная система решается методом прогонки за
8N арифметических операций.
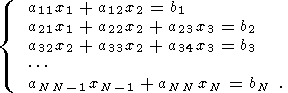
(51) 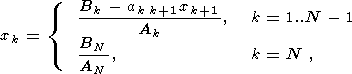
(52) 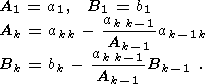
(53) 4.4. Построение результирующей кривой по точкам
отобранных примитивов
5. Программная реализация алгоритма на основе
объектно-ориентированного подхода
5.1. Внутренняя структура: классы и их взаимодействие
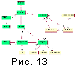
 Взаимодействие наиболее важных классов представлено на
UML-диаграммах (см. [Фаулер, Скотт, 1999]) взаимодействия классов
(рис. 13
и 14). Здесь
классы интерфейса (CWinApp, CMainFrame, CChildFrame, CWfdView,
CWfdDoc) выполняют все необходимые операции для обеспечения взаимосвязи
пользователя и программы с целью эффективной и удобной работы.
Взаимодействие наиболее важных классов представлено на
UML-диаграммах (см. [Фаулер, Скотт, 1999]) взаимодействия классов
(рис. 13
и 14). Здесь
классы интерфейса (CWinApp, CMainFrame, CChildFrame, CWfdView,
CWfdDoc) выполняют все необходимые операции для обеспечения взаимосвязи
пользователя и программы с целью эффективной и удобной работы.
5.2. Пользовательский интерфейс
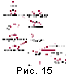 Пользовательский интерфейс ориентирован на использование
в
операционной системе MS Windows 95/98/NT. Допустима одновременная
работа с несколькими документами. Управление программой осуществляется
командами меню или панели инструментов. Работу пользователя с программой
можно кратко представить на рис. 15.
Пользовательский интерфейс ориентирован на использование
в
операционной системе MS Windows 95/98/NT. Допустима одновременная
работа с несколькими документами. Управление программой осуществляется
командами меню или панели инструментов. Работу пользователя с программой
можно кратко представить на рис. 15.
 Рассмотрим работу пользователя более подробно на примере
оцифровки
фрагмента сейсмограммы. Сначала загружаем и визуализируем изображение
сейсмограммы, хранимое в одном из основных графических форматов (TIFF,
PCX, BMP, JPEG). При этом оно преобразуется в двухцветное, где его серым
участкам соответствуют информационные области, а белым - фон (рис. 16).
На этом этапе пользователь может осуществлять геометрические
преобразования над изображением (поворот, отражение, переход к негативу,
сжатие) для его правильной ориентации. Операции осуществляются
соответствующими командами меню и панели инструментов.
Рассмотрим работу пользователя более подробно на примере
оцифровки
фрагмента сейсмограммы. Сначала загружаем и визуализируем изображение
сейсмограммы, хранимое в одном из основных графических форматов (TIFF,
PCX, BMP, JPEG). При этом оно преобразуется в двухцветное, где его серым
участкам соответствуют информационные области, а белым - фон (рис. 16).
На этом этапе пользователь может осуществлять геометрические
преобразования над изображением (поворот, отражение, переход к негативу,
сжатие) для его правильной ориентации. Операции осуществляются
соответствующими командами меню и панели инструментов.
 Затем по построенному скелету восстанавливаем искомую траекторию
(изображение самого скелета можно отключить, как это сделано на рис. 17).
Пользователь указывает сначала начальную точку, затем конечную. Искомая
траектория на указанном участке восстанавливается по построенному на
предыдущем этапе скелету. Якорь при этом перемещается к конечной точке,
чтобы служить началом следующего участка траектории (рис. 17).
Затем по построенному скелету восстанавливаем искомую траекторию
(изображение самого скелета можно отключить, как это сделано на рис. 17).
Пользователь указывает сначала начальную точку, затем конечную. Искомая
траектория на указанном участке восстанавливается по построенному на
предыдущем этапе скелету. Якорь при этом перемещается к конечной точке,
чтобы служить началом следующего участка траектории (рис. 17).
6. Примеры применения алгоритма и выводы
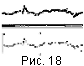
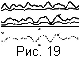 Качество распознавания существенно зависит от исходного
материала.
Для изображения следа самописца без самопересечений, где возможны
небольшие разрывы или наложения вертикальной сетки, может быть получен
достаточно хороший результат даже при выборе начальной и конечной точек
достаточно далеко друг от друга. Ниже представлены два фрагмента таких
записей: фрагмент магнитограммы (рис. 18) и фрагмент сейсмограммы (рис. 19)
(стрелками указаны соответствующие точки на исходном изображении и на
построенной траектории). Граничные точки для построения этих траекторий
выбирались только в начале и конце траектории.
Качество распознавания существенно зависит от исходного
материала.
Для изображения следа самописца без самопересечений, где возможны
небольшие разрывы или наложения вертикальной сетки, может быть получен
достаточно хороший результат даже при выборе начальной и конечной точек
достаточно далеко друг от друга. Ниже представлены два фрагмента таких
записей: фрагмент магнитограммы (рис. 18) и фрагмент сейсмограммы (рис. 19)
(стрелками указаны соответствующие точки на исходном изображении и на
построенной траектории). Граничные точки для построения этих траекторий
выбирались только в начале и конце траектории.
Литература
Загрузка файлов для печати и локального просмотра.
This document was generated by TeXWeb
(Win32, v.1.0) on January 31, 2001.
