Геометрические характеристики новейших тектонических движений
земной коры Северной Евразии
А. Ф. Грачев, Ш. А. Мухамедиев, В. А. Николаев
6. Обсуждение результатов
Проведенные выше исследования позволили построить набор карт
достаточно полной совокупности дифференциальных геометрических
характеристик новейших ВДЗК Северной Евразии. Проведение такого анализа
геометрических (точнее, кинематических) характеристик является абсолютно
необходимым первым шагом на пути построения геодинамической модели
новейшего развития литосферы.
В дифференциальных характеристиках кривизны поверхности снимается
зависимость от длинноволновых изменений амплитуды ВДЗК.(4)
Поэтому, если брать в расчет только кинематические факторы, то возникает
возможность провести классификацию новейших структурных форм не просто
по признаку активности вертикальных движений, а по комплексу гораздо более
тонких признаков - величин тех или иных характеристик кривизны или
корреляционных зависимостей между ними.
Другая важная задача, которую мы ставили перед собой, заключалась в
выявлении относительной важности той или иной геометрической характеристики
и возможности ее применения в геолого-геофизических приложениях. В этой связи
мы коснемся здесь, в основном, двух характеристик кривизны: гауссовой кривизны
H и интенсивности кривизны
Kint.
Гауссова кривизна (рис. 13) важна для решения вопроса
о возможности изометричного изгиба поверхности в некоторую другую заданную
поверхность (см. подробнее Приложение 2).
Для осуществления такой возможности
необходимо, чтобы обе эти поверхности обладали одинаковой гауссовой
кривизной. Если предположить, что доновейшая поверхность литосферы была
выровненной (т.е. ее гауссова кривизна была равна нулю) и тектонические
движения происходили так, что длина любой материальной линии вдоль
поверхности ВДЗК не изменялась, то образовавшаяся поверхность ВДЗК обязана
обладать нулевой гауссовой кривизной. Наоборот, если при исходной выровненной
поверхности образовавшаяся поверхность ВДЗК не принадлежит к
параболическому типу, то заведомо при тектонических деформациях длины линий
вдоль поверхности ВДЗК менялись. Вполне понятно, что затронутый вопрос имеет
прямое отношение к проблеме определения сокращения земной коры (СКЗ) при ее
изгибании вследствие тектонических движений.
Рассмотрим теперь некоторые другие геометрические параметры кривизны
поверхности ВДЗК. Весьма правдоподобным и часто используемым в
геофизической литературе является предположение, что деформирование
литосферы при ВДЗК происходит по типу изгиба тонкой пластины или оболочки
[см., например,
Мухамедиев, 1992;
Теркот, Шуберт, 1985;
Ershov, 1999;
Goetze and Evans, 1979].
Согласно гипотезе Кирхгофа-Лява, принятой в теории изгиба тонких
пластин и оболочек, при изгибе внутри пластины или оболочки существует
нерастяжимая (срединная) поверхность, а материальные элементы, ортогональные к
срединной поверхности до деформации, остаются нормальными к ней и после того,
как пластина или оболочка (а, следовательно, и срединная поверхность) претерпит
деформацию изгиба
[Амбарцумян, 1974;
Надаи, 1969].
На положение срединной поверхности внутри пластины или оболочки может влиять целый
ряд факторов
[Амбарцумян, 1974],
однако для простейшей модели однородной упругой
изотропной литосферы при изотермических условиях глубина срединной
поверхности в литосфере соответствует семантическому смыслу названия.
Предполагается, что на положение срединной поверхности
наиболее сильное влияние оказывают температурные изменения в литосфере
[Ershov, 1999].
Моделирование деформации литосферы изгибом тонкой пластины весьма
привлекательно для интерпретации определенных в настоящей работе
геометрических параметров в терминах деформаций, т.к. в уравнения изгиба (при
малых деформациях) в первом приближении не входят амплитуды горизонтальных
тектонических движений, о проблемах, определения которых по амплитудам ВДЗК
говорилось выше.
В работе
[Мухамедиев, 1992]
уравнения изгиба упругой однородной
изотропной литосферы были представлены в таком виде, что в выражение для
средних горизонтальных тектонических напряжений входит
Kmean, а в выражение
для максимального касательного напряжения в горизонтальной плоскости входит
безразмерный параметр
hKint/2g, где
h - мощность литосферы,
а
g - интенсивность горизонтальных глобальных сдвиговых
деформаций.
Соблазнительный вариант непосредственного перехода к определению тектонических
напряжений в литосфере по упомянутым формулам, на основе рассчитанных в
настоящей работе геометрических характеристик кривизны наталкивается на ряд
трудностей. Главной из них является отсутствие информации о глобальных
(передающихся от краев литосферной плиты) горизонтальных напряжениях,
которые не связаны напрямую с ВДЗК. К тому же нуждается в уточнении
предположение об упругом характере изгибания, т.к. рассматривается длительный
этап неотектонического развития. Поэтому необходимым этапом на пути к
определению напряжений является получение на основе геометрических
характеристик кривизны поверхности ВДЗК информации о возмущениях
деформированного состояния литосферы.
 А. Ф. Грачев и др. [1996],
используя необременительные предположения,
получили формулу, в которой тензор скорости неотектонической деформации
выражался через скорости изменения средней кривизны
Kmean и интенсивности
кривизны
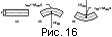
Kint. Здесь мы продемонстрируем связь характеристик кривизны
поверхности ВДЗК с возмущениями горизонтальных деформаций на простейшем
примере изгиба при выполнении гипотезы Кирхгофа-Лява (рис. 16). Возмущения
деформаций по глубине литосферы распределены линейно, причем экстремальные
(главные) значения деформаций достигаются в сечениях, совпадающих с сечениями
главных кривизн. На поверхности литосферы в направлении главной кривизны
Kmin реализуется максимальная, главная деформация
emax=-hKmin/2,
а в направлении
Kmax - минимальная главная деформация
emin=-hKmax/2.
А. Ф. Грачев и др. [1996],
используя необременительные предположения,
получили формулу, в которой тензор скорости неотектонической деформации
выражался через скорости изменения средней кривизны
Kmean и интенсивности
кривизны
Kint. Здесь мы продемонстрируем связь характеристик кривизны
поверхности ВДЗК с возмущениями горизонтальных деформаций на простейшем
примере изгиба при выполнении гипотезы Кирхгофа-Лява (рис. 16). Возмущения
деформаций по глубине литосферы распределены линейно, причем экстремальные
(главные) значения деформаций достигаются в сечениях, совпадающих с сечениями
главных кривизн. На поверхности литосферы в направлении главной кривизны
Kmin реализуется максимальная, главная деформация
emax=-hKmin/2,
а в направлении
Kmax - минимальная главная деформация
emin=-hKmax/2.
В разделе 5.3 было выявлено, что из всех характеристик кривизны наиболее
надежно определяется интенсивность кривизны
Kint. Эта характеристика
обладает и прозрачным геометрическим смыслом. Действительно из приведенных выше
рассуждений следует, что
Kint=2g/h, где
g= (e
max-emin)/2
- интенсивность деформаций
сдвига в верхних слоях литосферы. Последняя связана с максимальным
касательным напряжением и, по-видимому, с сейсмической активностью. Поэтому
характеристика интенсивности кривизны
Kint обладает особым значением по
сравнению с другими характеристиками кривизны. В частности, можно ожидать
корреляции
Kint(x, y) с пространственными особенностями
сейсмичности - накопленным сейсмическим моментом, максимально возможной
магнитудой землетрясений, их частотой и т.д.
7. Заключение
В работе исследованы геометрические характеристики деформирования
поверхности литосферы Северной Евразии, вызванные вертикальной составляющей
новейших тектонических движений, и построены соответствующие карты-схемы.
Выявлены особенности деформирования как для различных геоструктурных
областей, так и для отдельных регионов в их пределах, имеющих различный тип
тектонического развития. Проведенное исследование результатов на основе
визуального, факторного и корреляционного анализа, а также рассмотренные
модельные примеры показали наличие на изучаемой территории различных типов
деформирования. В частности, для орогенических и, в несколько меньшей степени
для платформенных областей, характерен параболический и гиперболический типы
поверхности ВДЗК, которым присуще наличие линейных антиклинальных и
синклинальных складок основания, а также участков, на которых главные кривизны
имеют разные знаки. Поверхность ВДЗК впадин глубоководных морей более близка
по типу к эллиптическим поверхностям, характеризуемым изометричными
прогибами с положительными главными кривизнами. Разные типы поверхности
имеют, по-видимому, разный физический механизм, вызывающий вертикальные
тектонические движения.
Если деформирование литосферы на выбранном при расчетах масштабном
уровне соответствует гипотезам, принятым в теории тонких пластин и оболочек, то
геометрические характеристики кривизны поверхности ВДЗК могут быть
истолкованы как кинематические характеристики кривизны изгиба литосферы.
Геометрические характеристики поверхности ВДЗК могут позволить
приблизиться к построению полей напряжений на основе постулирования связи
надежно определенных элементов поля деформаций с соответствующими
элементами напряженного состояния. Например, если принять, что модель изгиба
литосферы является адекватной, то полученные в настоящей работе результаты
после принятия той или иной реологической модели могут позволить определить
распределение таких силовых факторов как изгибающие моменты и
перерезывающие силы, а также получить приближенное распределение напряжений
по глубине. В любом случае, однако, напряжения, получаемые на основе данных о
ВДЗК, являются в некотором смысле возмущениями глобального двумерного поля
напряжений, возникающего из-за воздействия силовых факторов на границах
плиты. Само это поле, строго говоря, без дополнительных гипотез о взаимосвязи
ВДЗК с горизонтальными деформациями литосферы на основе используемых
данных определено быть не может.
This document was generated by TeXWeb
(Win32, v.1.0) on April 30, 2000.
 А. Ф. Грачев и др. [1996],
используя необременительные предположения,
получили формулу, в которой тензор скорости неотектонической деформации
выражался через скорости изменения средней кривизны
Kmean и интенсивности
кривизны
Kint. Здесь мы продемонстрируем связь характеристик кривизны
поверхности ВДЗК с возмущениями горизонтальных деформаций на простейшем
примере изгиба при выполнении гипотезы Кирхгофа-Лява (рис. 16). Возмущения
деформаций по глубине литосферы распределены линейно, причем экстремальные
(главные) значения деформаций достигаются в сечениях, совпадающих с сечениями
главных кривизн. На поверхности литосферы в направлении главной кривизны
Kmin реализуется максимальная, главная деформация
emax=-hKmin/2,
а в направлении
Kmax - минимальная главная деформация
emin=-hKmax/2.
А. Ф. Грачев и др. [1996],
используя необременительные предположения,
получили формулу, в которой тензор скорости неотектонической деформации
выражался через скорости изменения средней кривизны
Kmean и интенсивности
кривизны
Kint. Здесь мы продемонстрируем связь характеристик кривизны
поверхности ВДЗК с возмущениями горизонтальных деформаций на простейшем
примере изгиба при выполнении гипотезы Кирхгофа-Лява (рис. 16). Возмущения
деформаций по глубине литосферы распределены линейно, причем экстремальные
(главные) значения деформаций достигаются в сечениях, совпадающих с сечениями
главных кривизн. На поверхности литосферы в направлении главной кривизны
Kmin реализуется максимальная, главная деформация
emax=-hKmin/2,
а в направлении
Kmax - минимальная главная деформация
emin=-hKmax/2.