3-1. Изложенные в двух предыдущих разделах статьи основные положения и конструкции классической теории регуляризации (нахождения устойчивых приближенных решений, согласованных с имеющейся априорной информацией о помехе во входных данных и искомом решении) систем линейных алгебраических уравнений, с однозначностью свидетельствуют о том, что эта теория неадекватна реальной геофизической практике. Это однозначно следует из таких фактов:
1) в классической теории рассматривается только ситуация чисто аддитивных помех (в векторе правой части и матрицы), тогда как на практике достаточно часто встречаются и ситуации более общих мультипликативно-аддитивных помех;
2) в случае чисто аддитивных помех в задании правой части классическая теория основывается на допущении, что известной является величина d2 = ||df||2E квадрата эвклидовой нормы вектора помехи; фактически же эта величина никогда не бывает известна точно, в лучшем же случае бывают известны лишь постоянные в неравенствах
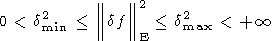 | (115) |
и неравенство
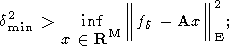 | (116) |
3) в подавляющем большинстве реальных геофизических ситуаций при наличии чисто аддитивной помехи в векторе правой части даже знание постоянных в неравенствах (115), если только имеет место ситуация, в которой
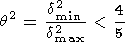 | (117) |
оказывается недостаточным для нахождения приближенного решения удовлетворительного качества;
4) наиболее эффективные алгоритмы, порожденные классической теорией, оказываются весьма трудоемкими и не могут быть использованы для нахождения устойчивых приближенных решений систем большой размерности;
5) приемы уменьшения трудоемкости основных алгоритмов, порождаемых классической теорией, основаны на использовании ортогональных преобразований, построенных на аннулировании основной части элементов симметричных положительно полуопределенных матриц; однако такие преобразования в случае систем большой размерности "отказывают" из-за влияния ошибок округления.
Понимание всей совокупности указанных фактов с очевидностью свидетельствует о том, что нужна новая теория регуляризации (нахождения устойчивых приближенных решений) систем линейных алгебраических уравнений с приближенными данными, существенно более адекватная реальной геофизической практике, которая порождала бы методы (алгоритмы), более эффективные - по показателям точности и быстродействия - в случае систем большой размерности.
Подобная теория была разработана на протяжении последнего десятилетия В. Н. Страховым, [см. Страхов, 1991a, 1991b, 1991c, 1992a, 1992b, 1997d, 1997e, 1997f, 1997g, 1997h; Страхов, Тетерин, 1991a, 1991b, 1991c, 1993; Strakhov et al., 1995]; в последние годы в разработке этой новой теории и ее практической реализации принял участие и А. В. Страхов [Страхов, Страхов, 1998, 1999a, 1999b, 1999c, 1999d]. Изложению основных позиций этой новой теории и посвящены настоящий и следующий разделы статьи.
3-2. В классической теории регуляризации исходной системе (1) сопоставляется ее аппроксимация (2) (чисто аддитивная помеха только в правой части) и (62)-(63), (65) (аддитивная помеха в правой части и матрице). В рамках новой теории кроме указанных рассматриваются ситуации задания аппроксимаций
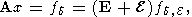 | (118) |
где фактически задан вектор fd, E, и
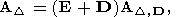 | (119) |
где фактически заданы матрица
AD, D и вектор
fd, E. Здесь E - единичная
(N
при этом
так что матрицы
(E + e) и
(E + D) являются
невырожденными.
Ниже будет показано, что случаи аппроксимаций (118), (120) и (119), (120) при
условиях (121) в определенном смысле редуцируются к случаю аппроксимации (2),
т.е. наличию чисто аддитивной помехи в задании правой части системы (1).
Поэтому изложение основ новой теории целесообразно начать с рассмотрения
основного частного случая задания аппроксимации (2) системы линейных уравнений
(1).
3-3. Основой новой теории в случае чисто аддитивной помехи в векторе
правой части
системы являются следующие четыре положения.
1. Основная вычислительная процедура в любом методе - алгоритме - состоит
в нахождении последовательности приближенных решений
x(k),
k = 1, 2,
и величин
При этом каждое приближение
x(k) характеризуется некоторым
набором (вектором) параметров счета, то есть величин, по которым находится
приближенное решение; обычно размерность вектора парамет-
ров счета - от
одного до трех. Желательно (хотя это и не всегда может быть гарантировано),
монотонное убывание величин
vk:
Следует подчеркнуть, что нахождение последовательности приближенных решений
x(K) отнюдь не означает, что используется какой-то итерационный
процесс. Например, речь может идти о нахождении решений уравнения
для последовательности значений
ak,
k = 1, 2,
2. В каждом методе (алгоритме) присутствует некоторый вектор
показателей качества решения; в этом векторе выделяются
основные показатели качества решения (обычно - от
одного до трех), и дополнительные показатели. С помощью основных
показателей качества решений выделяются, среди всех приближенных решений
x(k), так называемые пробные решения, с помощью
же дополнительных показателей качества решений множество пробных решений
сокращается до множества допустимых ре- шений.
Ясно, что с помощью основных показателей качества решения формируется и
правило останова процесса нахождения приближенных решений.
Ясно также, что в процессе счета должны запоминаться все пробные решения - и
далее, после сужения множества пробных решений до множества допустимых решений,
все допустимые решения.
В ситуации, когда известны постоянные в неравенствах (115), используется обычно
один показатель качества - величина
при этом пробными являются все те приближенные решения, для которых
Процесс построения приближенных решений останавливается, коль скоро оказывается
Кроме основного показателя качества (126) могут использоваться и другие основные
показатели, например:
Здесь
x(kmin) - пробное решение с наименьшим значением
k;
при этом используется правило останова процесса построения последовательных
приближений
где Crit - априорно заданная величина.
Что касается дополнительных показателей качества, то в рассматриваемом
случае это могут быть различного рода числовые величины, порождаемые априорной
информацией о векторе помехи
df.
Принципиально важно, что если имеет место ситуация, в которой выполняется
неравенство (117), то именно последняя информация должна использоваться
для задания основных показателей качества решения. Эта ситуация подробнее
рассматривается ниже. В ней по существу нахождение множеств пробных и
допустимых решений осуществляется с помощью эвристических процедур типа
распознавания образов.
3. После того, как найдено множество допустимых приближенных решений системы
(2), возникает проблема нахождения искомого - или окончательного, или
оптимального - устойчивого приближенного решения. Эта проблема в рамках
новой теории решается на основе принципа усреднения допустимых решений:
где весовые коэффициенты
pk имеют свойства
Здесь
Jk - подмножество значений индекса
k для допустимых
решений.
Ясно, что здесь возникает новая проблема - задания весовых множителей
pk.
Эта проблема детально обсуждается ниже, но сразу же подчеркнем тот факт, что и
здесь основное значение имеют различного рода эвристические процедуры, и в
конечном итоге - технологии распознавания образов.
4. Все три предыдущих положения относились к так называемой нормальной
ситуации, в которой:
а) в последовательности приближенных решений
x(k) всегда
содержатся пробные приближенные решения, а останов процедуры построения
приближенных решений осуществляется по значениям основных показателей качества
приближенных решений;
б) число находимых допустимых решений, усреднением которых, см. (131)-(132),
находится окончательное решение, достаточно велико:
где
R0 - заданная величина.
Однако на практике, как это показали достаточно многочисленные расчеты
(описание которых будет дано в четвертой части работы), кроме нормальной,
может встречаться и аномальная ситуация, в которой:
а) либо число найденных допустимых решений меньше
R0 (см. (133));
б) либо вообще не находятся пробные (тем более - допустимые) приближенные
решения.
В указанных ситуациях алгоритмы должны обеспечивать:
- в случае а) (число допустимых решений меньше
R0 )
нахождение дополнительных допустимых решений;
- в случае б) (отсутствие пробных или допустимых решений) нахождение
некоторого - единственного! - приближенного решения, которое и принимается
за окончательное.
Здесь следует сразу же акцентировать внимание читателя на том обстоятельстве,
что в рамках классической теории некорректно поставленных задач (по существу не
адекватной реальной геофизической практике) никакие аномальные ситуации
(обусловленные погрешностями округлений) по существу не принимались во внимание
и не обсуждались.
В заключение параграфа подчеркнем, что практическая реализация установок новой
теории требует создания принципиально новых компьютерных технологий, в которых
в некотором смысле определяющее значение имеют управляющие подпрограммы,
с помощью
которых формируются последовательности векторов параметров счета - для нахождения
последовательных приближений, а также осуществляется анализ получаемых
приближенных решений - по значениям показателей качества решения, в целях,
по существу, ответа на вопрос - "что такое хорошо, и что такое плохо".
Эта управляющая программа одновременно должна обеспечивать перестройку
вычислительного процесса в случае аномальных ситуаций.
3-4. В рамках новой теории регуляризации систем линейных алгебраических
уравнений, ориентированной на создание компьютерных технологий, полностью
адекватных реальной геофизической практике, и на решений систем линейных
алгебраических уравнений большой и сверхбольшой размерности, используется
ряд принципиально новых математических объектов и конструктивных идей.
Обсуждению конструктивных идей посвящен последний раздел настоящей статьи
и вторая часть работы, поэтому здесь остановимся лишь на некоторых новых
математических объектах.
Первая группа объектов связано с оценками предельной
относительной погрешности любых приближенных решений систем (1), заданных
аппроксимациями (2), при использовании представлений
здесь
Оценочный функционал в случае аппроксимации (2) имеет вид
Ясно, что к числу новых объектов первой группы принадлежит и сама матрица
Вторая группа объектов связана с идеей более глубокого понимания метода
наименьших квадратов и соответственно - перенесения ряда важных свойств
решений, получаемых в методе наименьших квадратов, на регуляризованные решения.
Здесь прежде всего следует отметить характеристическое уравнение метода
наименьших квадратов (26) и тот факт, что в вариационном методе
А. Н. Тихонова оно не выполняется. Но легко показать, что если
x есть некоторое приближенное решение, для которого
то приближенное решение
в котором принято
уже удовлетворяет характеристическому уравнению метода наименьших квадратов
При этом
Все эти факты легко получаются, если рассмотреть задачу
Ясно, что соотношение
где
d2 - априорно заданная величина, эквивалентно
соотношению
Выполнение же характеристического уравнения метода наименьших квадратов имеет
принципиальное значение в тех (весьма часто встречающихся на практике) случаях,
когда априорно известно, что полезный сигнал
f и помеха
df ортогональны:
Далее. Из основного уравнения в методе наименьших квадратов следует, что
( x0 - решение системы(23)):
Отсюда, как нетрудно найти, следует, что имеют место равенства
где
a(i) суть векторы-столбцы матрицы
A, т.е. что вектор невязки
для решения, найденного по методу наименьших квадратов, ортогонален ко всем
столбцам матрицы
A. Далее естественно ввести и использовать
квадратичный функционал
где
для которого имеет место оценка
и который при
x = x0 (решению, получаемому по методу наименьших квадратов)
обращается в ноль.
Третья группа объектов, культивируемых в новой теории
регуляризации систем линейных алгебраических уравнений, это новые ортогональные
преобразования. Точнее, речь идет об ортогональных преобразованиях вида
в которых
V и
U суть ортогональные по столбцам матрицы
размеров (N
в которых
Vk и
Uk суть ортогональные по
столбцам матрицы указанного выше вида. Так вот, речь идет о том, что параметры
( cosj и
sinj, где
j имеет соответствующие индексы)
матриц элементарных плоских вращений выбираются совсем по-иному, чем в широко
используемых в настоящее время процедурах. В последних (приведение к
треугольной или двухдиагональной формам, к трехдиагональной или диагональной
формам) параметры вращения выбираются из условия аннулирования некоторого
элемента матрицы. В новых процедурах, разработанных В. Н. Страховым и
А. В. Страховым
(см. [Страхов, 1997d, 1997e, 1998d;
Страхов, Страхов, 1999b, 1999c,
1999d;
Страхов, Тетерин, 1993;
Strakhov et al., 1995]),
параметры преобразований выбираются из иных условий.
Наиболее важными новыми ортогональными преобразованиями являются:
1) процедура выметания одного столбца в другой;
2) процедура выметания одной строки в другую;
3) процедура раскорреляции данного столбца с данным вектором - за счет
преобразования данного столбца с некоторым третьим (опорным);
4) процедура максимизации коэффициента корреляции некоторого (опорного)
столбца с заданным - за счет преобразования этого столбца с некоторым третьим,
и ряд других, которые здесь обсуждать не будем, ибо эта тема будет подробно
рассмотрена во второй части работы.
Значимость для вычислительной алгебры в целом, а не только для новой теории
регуляризации систем линейных алгебраических уравнений, аппарата
ортогональных преобразований видна из следующего примера. Пусть ортогональное
преобразование (150) при V
и
где
b(j) - векторы-столбцы матрицы B. В этом случае получаем
(для системы (2))
где
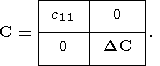
и матрица C = B
T B имеет следующую структуру
Ясно, что решение системы (154) редуцируется к одному уравнению с одним
неизвестным
которое элементарным образом регуляризуется
где
a > 0 - параметр. Далее используются соотношения
Таким образом, использование подходящих ортогональных преобразований позволяет
получить весьма эффективный по быстродействию алгоритм, ибо
считать матрицу
D C вовсе не нужно!
Далее необходимо указать, что в построении целого ряда новых ортогональных
преобразований матриц центральную роль играет сформулированная В. Н. Страховым
концепция выметания матриц
[Страхов, 1997e].
Ее суть в следующем: пусть в множестве всех пар индексов
(i, j),
1
Рассматриваются две задачи:
первая - найти ортогональные по столбцам матрицы V и U,
размеров (N
где O
N и O
M - множества всех ортогональных по
столбцам матриц размеров (N
вторая - найти те же самые ортогональные по столбцам матрицы V и U
из условия
Поскольку, как хорошо известно
[см. Воеводин, Кузнецов, 1984;
Марчук, Кузнецов, 1972;
Уилкинсон, Райнш, 1976;
Фаддеев, Фаддеева, 1963]);
то задачи (160) и (161) эквивалентны; ими определяются такие ортогональные
преобразования, которые осуществляют перераспределение эвклидовой нормы
матрицы A или выметание A в J. Очевидно, наиболее важным является
тот случай, когда
т.е. когда осуществляется полное выметание матрицы A на
подмножество J, так что если V
T AU = B и
bi,j суть
элементы B, то
Ясно, что всегда можно выбирать матрицы V и U в форме
где T
ip, jp(jp)
и T
iq, jq(yq)
суть
элементарные матрицы плоских вращений; при этом параметры вращения у этих
матриц определяются в соответствии с основной постановкой - (160) или (161).
Во второй части работы будет подробно рассмотрен ряд конкретных ортогональных
преобразований подобного типа.
Четвертая группа объектов - итерационные процессы нового типа,
порождаемые последовательностями ортогональных преобразований матриц. Здесь
существует большое разнообразие возможностей, которые будут подробно
рассмотрены во второй части работы.
Наконец, пятая группа объектов - это различного рода функционалы,
определяемые:
а) на векторах невязок
r(k) = fd
- A x(k);
б) на приближенных решениях
x(k).
3-5. Обсудим теперь более подробно один из принципиальных элементов
новой теории - оценки предельной относительной погрешности приближенных
решений
x, получаемых по соотношению (134), в котором
есть некоторая заданная матрица размера (M
Элементарные выкладки, в которых сначала используется схема Лаврентьева-Джона
(6), с заменой
d на
, и далее очевидные неравенства
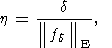
приводят к следующему результату
где
При этом в (167) и (168)
|
Далее - пусть известна лишь аппроксимация (62) уравнения (1), т.е. с погрешностью
заданы и правая часть, и матрица системы. В этом случае вводится оценочный функционал
Очевидно, имеем
где положено
Из неравенства (171) следует, что в случае задания аппроксимации (62)
системы (1) можно принять, что матрица A
D есть точная матрица,
но правая часть
fd задана с помехой
df большей нормы,
а именно
где
и
Изложенная схема редукции задач нахождения устойчивых приближенных решений
систем линейных алгебраических уравнений с приближенно заданными правыми
частями и матрицами (помехи чисто аддитивные) к случаю задания аддитивной
помехи только в правой части системы безусловно является принципиальной
частью новой теории регуляризации систем линейных алгебраических уравнений.
Отметим здесь еще одно важное следствие оценки (171). Ясно, что если матрица
A - квадратная, N=M, но вырожденная или очень плохо обусловленная, то тогда
разумно перейти от матрицы A к матрице
AD = A + D
A с помощью искусственно введенного
возмущения
D A, введенного таким образом, чтобы матрица
D A была уже разумным образом обусловлена.
В таком случае,
очевидно, разумно выбрать
в этом случае оценка предельной относительной погрешности примет вид
где
и
Очевидно, в оценке (177)-(179) могут фигурировать либо спектральные, либо
эвклидовы норма матриц A
D и A
-1D. Ясно, из общих
соображений (значение которых будет подробно рассмотрено во второй части
работы), что целесообразно ввести следующее условие на вариацию
D A матрицы A (в тех случаях, когда вариация
осуществляется
в целях регуляризации):
при этом наиболее важным практически будет случай, когда в (178), (180)
фигурирует эвклидова норма матриц.
Далее ясно, что подобного рода оценки могут быть (и даже обязательно
должны быть) использованы и в том случае, когда рассматриваются системы
линейных уравнений
и
и т.д. Расписывание соответствующих оценок предоставляется читателю. При этом
ясно, что случай систем (181), равно как и систем
является с точки зрения практики особенно важным, ибо матрицы C и
CO - квадратные, размеров
(M
Ясно одновременно, что случай систем (181) вписывается в изложенную выше схему,
если просто принять в (134)
а случай систем (183) - если принять
в (184)
Забегая вперед (подробно этот вопрос будет рассматриваться во второй части
работы), отметим также, что полученные оценки предельной относительной
погрешности позволяют ввести в рассмотрение новые постановки безусловных
и условных экстремальных задач, например
или
где
D2 - априорно заданное число (см. соотношения
(62), (65), и (177)-(179)).
Введение новых постановок безусловных и условных экстремальных задач - одна из
отличительных черт новой теории регуляризации систем линейных алгебраических
уравнений с приближенными данными.
3-6. Переходим к рассмотрению еще одной принципиальной стороны новой
теории
регуляризации систем линейных алгебраических уравнений - постановок задач
построения регуляризованных алгоритмов в ситуации мультипликативно-аддитивных
помех, в простейшем случае - в задании правой части системы, в более общем - в
задании как правой части, так и матрицы системы, см. (118), (120)-(121);
в этой связи см. работы
[Страхов, 1991d, 1991e, 1991f,
1991g,
1991h, 1991i].
Начнем со случая задания аппроксимации (118), (120)-(121) системы (1).
Наша основная цель состоит в том, чтобы установить факт принципиальной
редукции задачи к нахождению устойчивого приближенного решения системы
типа (2), т.е. к случаю чисто аддитивной помехи.
Пусть, как сказано выше,
ei - суть компоненты диагональной
матрицы e. Рассмотрим задачу
где
g>0 - параметр (который, вообще говоря, не имеет
смысла параметра
регуляризации), а
aT(i) -
i -ая вектор-строка матрицы A.
Выполняя элементарные дифференцирования по
ei и приравнивая
производные нулю, с очевидностью получаем следующие соотношения:
и при этих значениях
ei
где
Pg и
Qg суть диагональные матрицы
с элементами
pi(g) и
qi(g), соответственно
равными:
Из (189)-(191) и (192), (193) следует, что если задана аппроксимация (118)
системы (1), то фактически имеет место редукция к случаю задания
аппроксимации (2), но с одним важным изменением. Именно, и в случае (118) для
нахождения устойчивых приближенных решений системы (1) можно использовать
алгоритмы, разработанные для аппроксимации (2), но при этом:
а) необходимо иметь априорную информацию как о векторе помехи
df,
так и о диагональной матрице помехи e;
б) в числе основных показателей качества приближенных решений
x(k) должны использоваться величины:
при этом, если величина
априорно известна, то по ней должно определяться, в соответствии с (191),
значение
g = gk
для каждого приближения
x(k).
Если же величина
e2 неизвестна, а известны лишь оценки
для нее сверху и снизу
то ситуация сложнее - здесь необходимо использовать технику распознавания
образов, основанную на совокупности множества показателей качества решения.
Можно, однако, ставить задачу построения оптимальных решений и в случае, когда
вообще отсутствует информация о величинах
||df||E и
||e||E.
Далее. После всего сказанного о случае мультипликативно-аддитивной помехи в
задании правой части системы легко понять, что более общий случай задания и
правой части, и матрицы системы с мультипликативно-аддитивной помехой
редуцируется к случаю чисто аддитивных помех в задании правой части и матрицы.
Это следует из простейшего преобразования аппроксимации (119) к виду
где
и
eO есть диагональная матрица с элементами
Все остальное, в свете сказанного в данном параграфе относительно редукции
аппроксимации (118) к аппроксимации (2), должно быть читателю достаточно
очевидно.
3-7. Остается лишь высказать некоторые дополнительные соображения по
поводу использования методов (алгоритмов) распознавания образов в процессе
нахождения искомого устойчивого приближенного решения системы (1), заданной
какой-либо аппроксимацией. Признание того, что без использования процедур
распознавания в задаче нахождения устойчивых приближенных решений систем
линейных алгебраических уравнений большой (тем более - сверхбольшой)
размерности обойтись нельзя - принципиально важный элемент новой
теории регуляризации, адекватной реальной геофизической практике.
Выше уже по существу было сказано, что распознавание образов может быть
(и практически - должно!) использоваться в трех вариантах:
а) в анализе ситуации - нормальная она или аномальная;
б) при нахождении множеств пробных и допустимых приближенных решений;
в) при нахождении искомых - окончательных - приближенных решений на основе
использования "принципа усреднения" допустимых решений, в специальной
процедуре нахождения весовых коэффициентов
pk.
Фактически процедуры распознавания образов реализуются в двух формах:
1) в форме рангового распознавания;
2) в форме эвристических процедур проверки некоторой совокупности логических
условий, обычно - типа равенств и неравенств.
Ранговое распознавание используется в процедурах назначения весов и выделения
множеств допустимых решений. Его суть в следующем. Пусть задано некоторое
множество приближенных решений и для него необходимо указать совокупность
некоторых характеристических числовых показателей. Например, в задаче
сокращения множества пробных решений до множества допустимых решений такими
показателями являются числа 1 и 0, 1 - для допустимых решений, 0 - для тех,
которые не включаются в число допустимых. Равным образом в задаче нахождения
весовых коэффициентов в правиле усреднения (131)-(132) допустимых решений
эти коэффициенты и представляют собой характеристические числовые показатели.
Процедура рангового распознавания состоит в том, что вводится так называемое
"признаковое пространство"; при этом роль "признаков" выполняют значения
различных функционалов на приближенных решениях; обозначим эти функционалы
wq,q = 1, 2,
Далее по найденным суммарным рангам и осуществляется нахождение характеристических
числовых показателей. В задаче выделения допустимых решений назначается некоторое
число Crit, и если выполняется неравенство
то данному приближенному решению
x(k) сопоставляется
характеристический числовой показатель 1, т.е.
x(k) считается допустимым решением; если же неравенство
(203) места не
имеет, то приближенному решению
x(k) сопоставляется
характеристическое число 0, т.е. это приближенное решение допустимым
не считается.
В задаче же определения весовых множителей
pk в принципе усреднения
пробных решений используется формула
в которой
Теперь относительно процедур распознавания образов, основанных на использовании
эвристических процедур проверки совокупности логических условий. Эти процедуры
поясним на важнейшем примере выделения множеств пробных решений в ситуации,
когда либо постоянные в неравенствах (115) неизвестны, либо нарушается
условие достаточной близости
d2min к
d2max, см. (117).
В данных процедурах также используется набор функционалов
Wp(x)
где
C2min(p) и
C2max(p) суть заданные постоянные, то
приближенное решение
x(k) является кандидатом в пробные
решения по функционалу
WP(x). Принимается, что
если данное
приближенное решение
x(k) является кандидатом в пробные
по заданной доле всех функционалов
Wp(x) (например, оно
является
кандидатом в пробные не менее чем по 3/4 от общего числа функционалов),
то оно причисляется к числу пробных. Критерии останова процедуры
нахождения пробных решений с помощью проверки логических условий могут
быть различными:
а) уже найдено априорно заданное число пробных решений;
б) подряд для заданного числа приближенных решений ни одно из них не оказалось
принадлежащим к числу пробных (после того, как некоторое число пробных решений
было уже найдено);
- и т.д., и т.п.
Во второй части работы оба основных подхода к использованию методов
распознавания образов в компьютерных алгоритмах нахождения устойчивых
приближенных решений систем линейных алгебраических уравнений с приближенными
данными будут дополнительно обсуждены.
3-8. И самое последнее в данном разделе, посвященном изложению основных
положений новой теории регуляризации систем линейных алгебраических уравнений
с приближенными данными. В п. 1-2 было проведено классическое
определение регуляризующего алгоритма по А. Н. Тихонову,
[см. Иванов и др., 1978;
Лисковец, 1981;
Морозов, 1974, 1987;
Танана, 1981;
Тихонов, Арсенин, 1979;
Тихонов и др., 1985].
В течение достаточно длинного периода (по крайней мере в 60-е-70-е годы)
главным в теории линейных некорректных задач было именно доказательство
регулярности различных конкретных алгоритмов,
[см. Алифанов и др., 1998;
Воеводин, 1969;
Иванов, 1962, 1966, 1977;
Иванов и др., 1978;
Лаврентьев, 1955, 1959, 1962;
Лисковец, 1981;
Лоусон, Хенсон, 1986;
Морозов, 1973, 1974, 1987;
Танана, 1981].
Однако в дальнейшем было понято, что теоретического обоснования регулярности
недостаточно, ибо наличие ошибок округления при реализации регулярных методов
на практике может радикально изменять ситуацию. Именно по этой причине в данной
статье доказательства регулярности различных обсуждаемых алгоритмов не
приводятся.*)
В новой теории регуляризации систем линейных
алгебраических уравнений с приближенными данными упор делается на других
моментах:
1) нахождения достаточно точных и устойчивых приближенных решений систем в
условиях большой априорной неопределенности в информации об искомом решении
и полезном сигнале, а также помехах;
2) эффективности алгоритмов по быстродействию (что принципиально важно в случае
систем большой и сверхбольшой размерности);
3) использовании распознавания образов для выделения допустимых решений и
назначении коэффициентов в принципе усреднения допустимых решений.
По указанным причинам во второй части работы при описании конкретных методов
проблема собственно регулярности алгоритмов нахождения допустимых решений
рассматриваться не будет; этот аспект в рамках новой теории не имеет
сколько-нибудь определяющего значения.
 N)-матрица, а
e и
N)-матрица, а
e и
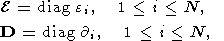
(120) 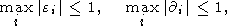
(121)  , и
соответствующих им векторов невязок
, и
соответствующих им векторов невязок
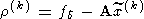
(122) 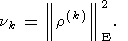
(123) 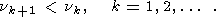
(124) 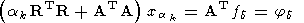
(125)  ; в этом
случае
x(k) = xak
и
ak суть параметр счета
(единственный).
; в этом
случае
x(k) = xak
и
ak суть параметр счета
(единственный).
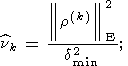
(126) 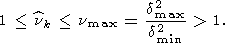
(127) 
(128) 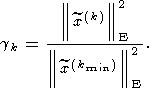
(129) 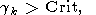
(130) 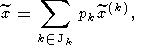
(131) 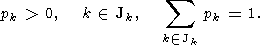
(132) 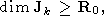
(133) 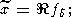
(134)  суть (M
суть (M N)-матрица, заданная либо определяемая некоторыми
условиями.
N)-матрица, заданная либо определяемая некоторыми
условиями.
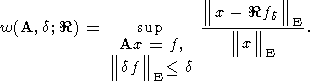
(135)  ,
и функционал
w( A,d;
,
и функционал
w( A,d; 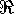 ), и другие подобного
рода функционалы,
и следующие из оценок предельной относительной погрешности приближенных решений
новые постановки безусловных и условных экстремальных задач, и многие другие
объекты.
), и другие подобного
рода функционалы,
и следующие из оценок предельной относительной погрешности приближенных решений
новые постановки безусловных и условных экстремальных задач, и многие другие
объекты.
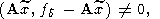
(136) 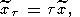
(137) 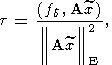
(138) 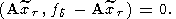
(139) 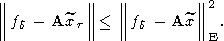
(140) 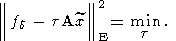
(141) 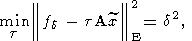
(142) 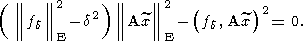
(143) 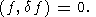
(144) 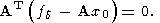
(145) 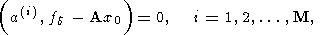
(146) 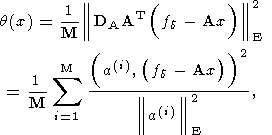
(147) 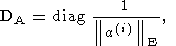
(148) 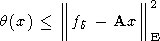
(149) 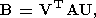
(150)  N) и (M
N) и (M
 M), соответственно, и которые представимы
в форме произведений элементарных матриц плоского вращения, либо вида
M), соответственно, и которые представимы
в форме произведений элементарных матриц плоского вращения, либо вида
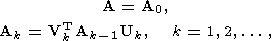
(151)  E
осуществлено таким образом, что выполняются условия
E
осуществлено таким образом, что выполняются условия
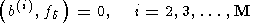
(152) 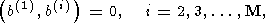
(153) 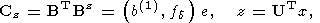
(154) 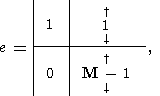
(155) 
(156) 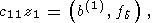
(157) 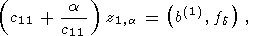
(158) 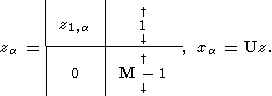
(159)  i
i  N,
1
N,
1 j
j  M;
выделено некоторое
подмножество J пар индексов
(i, j), которое является односвязным;*)
через CJ обозначается подмножество пар индексов
(i, j), получаемое из
полного множества удалением подмножества J (ясно, что CJ уже может не быть
связным множеством).
M;
выделено некоторое
подмножество J пар индексов
(i, j), которое является односвязным;*)
через CJ обозначается подмножество пар индексов
(i, j), получаемое из
полного множества удалением подмножества J (ясно, что CJ уже может не быть
связным множеством).
 N) и (M
N) и (M
 M), соответственно, из условия
M), соответственно, из условия
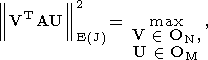
(160)  N) и (M
N) и (M
 M), соответственно,
|
M), соответственно,
| |2E(J) -
эвклидова норма матрицы,
определенная по элементам, имеющим пары индексов
(i, j), принадлежащих
подмножеству J;
|2E(J) -
эвклидова норма матрицы,
определенная по элементам, имеющим пары индексов
(i, j), принадлежащих
подмножеству J;
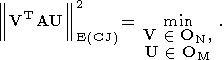
(161) 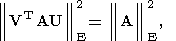
(162) 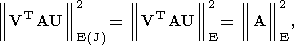
(163) 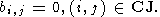
(164) 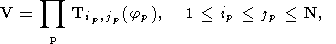
(165) 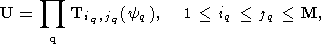
(166)  N)
(в общем случае N
M). Предполагается при этом, что точное решение
x системы (1) существует.
N)
(в общем случае N
M). Предполагается при этом, что точное решение
x системы (1) существует.
 | E - A|
| E - A| |x|E,
|x|E,
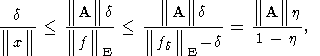
(167) 
 |E - A|
|E - A| 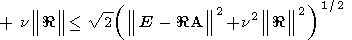
(168)  2(| E - A|2E
+ n2||2E)1/2,
2(| E - A|2E
+ n2||2E)1/2,
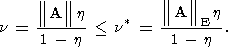
(169)  | суть спектральные нормы матриц,
а
|
| суть спектральные нормы матриц,
а
| |E - эвклидовы нормы матриц.
|E - эвклидовы нормы матриц.
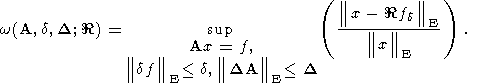
(170)  | E
- A|+ n||
| E
- A|+ n||  | E - ( AD
- D A )|+ n
| E - ( AD
- D A )|+ n ||
||  )||
)|| 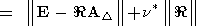
(171)  2 (| E - AD|2
+ (n
2 (| E - AD|2
+ (n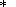 )2||2)1/2
)2||2)1/2
 2(| E - AD|2
+ ( n
2(| E - AD|2
+ ( n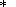 )2||2E)1/2,
)2||2E)1/2,
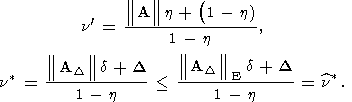
(172) 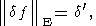
(173) 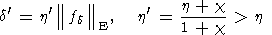
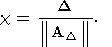
(174) 
(175) 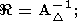
(176) 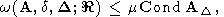
(177) 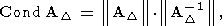
(178) 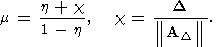
(179) 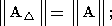
(180) 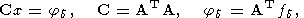
(181) 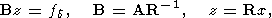
(182) 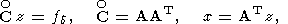
(183)  M) и (N
M) и (N
 N), соответственно, и C = C
T,
CO = CTO
N), соответственно, и C = C
T,
CO = CTO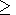 0.
0. 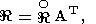
(184) 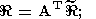
(185) 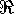 O есть
(M
O есть
(M M)-матрица, а в
(185)
M)-матрица, а в
(185) 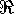 ~ есть
(N
~ есть
(N N)-матрица.
N)-матрица.
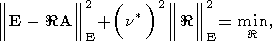
(186) 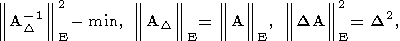
(187) 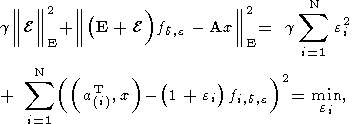
(188) 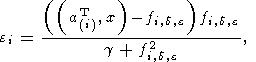
(189) 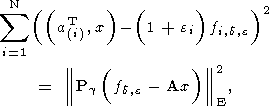
(190) 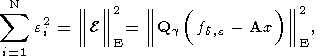
(191) 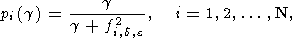
(192) 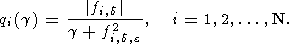
(193) 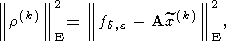
(194) 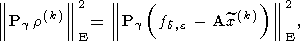
(195) 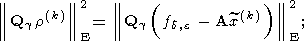
(196) 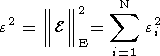
(197) 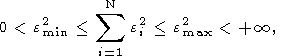
(198) 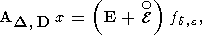
(199) 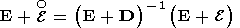
(200) 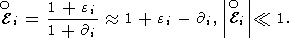
(201)  , Q, а значения (неотрицательных)
функционалов на приближенных решениях
x(k),
k = kmin,
kmin + 1,
, Q, а значения (неотрицательных)
функционалов на приближенных решениях
x(k),
k = kmin,
kmin + 1, , kmax,
через
wq( x(k))
= wq, k. Принимается,
что все признаки
(функционалы
wq ) введены так, что чем
меньше значение
wq, k > 0, тем приближенное
решение
x(k) по
данному признаку лучше. Совокупность приближенных решений
{x(k)}k=kmink=kmax
ранжируется
по каждому признаку; соответствующие ранги
rgwq, k изменяются
от 1 до
k = (kmax) - kmin + 1. При этом
ранг 1 приписывается тому приближенному решению
x(k), для
которого
wq, k = mink,
ранг 2 - тому, для которого
wq, k = mink
из всех остальных приближенных решений,
и т.д., смысл процедуры назначения рангов по
q -му признаку ясен. Таким
образом определяются ранги приближенных решений
x(k),
kmin
, kmax,
через
wq( x(k))
= wq, k. Принимается,
что все признаки
(функционалы
wq ) введены так, что чем
меньше значение
wq, k > 0, тем приближенное
решение
x(k) по
данному признаку лучше. Совокупность приближенных решений
{x(k)}k=kmink=kmax
ранжируется
по каждому признаку; соответствующие ранги
rgwq, k изменяются
от 1 до
k = (kmax) - kmin + 1. При этом
ранг 1 приписывается тому приближенному решению
x(k), для
которого
wq, k = mink,
ранг 2 - тому, для которого
wq, k = mink
из всех остальных приближенных решений,
и т.д., смысл процедуры назначения рангов по
q -му признаку ясен. Таким
образом определяются ранги приближенных решений
x(k),
kmin  k
k  kmax, по всем признакам
q, 1
kmax, по всем признакам
q, 1 q
q Q.
Далее осуществляется процедура определения для каждого приближенного
решения суммарного ранга,
Q.
Далее осуществляется процедура определения для каждого приближенного
решения суммарного ранга,
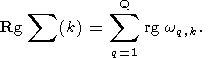
(202) 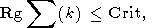
(203) 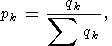
(204) 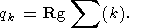
(205) 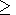 0,
p = 1, 2,
0,
p = 1, 2,  , P, при этом вводятся
условия в форме неравенств,
выделяющие пробные решения; если
, P, при этом вводятся
условия в форме неравенств,
выделяющие пробные решения; если
(206)
This document was generated by TeXWeb
(Win32, v.1.0) on July 4, 1999.