1. Краткая характеристика классической теории регуляризации систем линейных алгебраических уравнений с приближенными данными

1-1. Проблема нахождения приближенных решений систем линейных алгебраических уравнений с приближенными данными имеет, по существу, длительную историю, см., например, [Альберт, 1977; Лоусон, Хенсон, 1986]. Но громадный прогресс в решении этой проблемы был обусловлен созданием общей теории некорректно поставленных задач, основоположником которой является академик А. Н. Тихонов, и существенный вклад в которую внесли член-корреспондент В. К. Иванов и академик М. М. Лаврентьев и затем их ученики [Алифанов и др., 1998; Воеводин, 1969; Иванов, 1962, 1966, 1977; Иванов и др., 1978; Лаврентьев, 1955, 1959, 1962; Лисковец, 1981; Морозов, 1973, 1974, 1987; Танана, 1981; Тихонов, 1943, 1963a, 1963b, 1965; Тихонов, Арсенин, 1979; Тихонов и др., 1985]. Ниже излагаются те результаты этой общей теории, которые относятся к проблеме регуляризации линейных систем с аддитивной помехой в задании правой части.

1-2. Пусть требуется найти "достаточно хорошее" ("разумное"”) приближенное решение (псевдорешение) системы линейных алгебраических уравнений

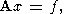(1)

по заданной аппроксимации этой системы

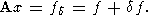(2)

В (1)-(2) A суть (N M)-матрица с вещественными элементами a_ij, 1 i N, 1 j M, N - число неизвестных (в общем случае N M), x есть искомый M-вектор, f_d - заданный N-вектор, f есть вектор полезного сигнала, df - вектор помехи (которая предполагается случайной).

В классической теории регуляризации систем линейных алгебраических уравнений (1)^*) всегда принимается, что векторы x и f, для которых выполняется соотношение (1), существуют. Одновременно предполагается, что правая часть в неравенстве

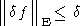(3)

известна.^*)

В классической теории регуляризации систем (1) ставится вопрос о построении приближенных решений системы (2), в форме

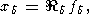(4)

где 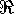_d есть (MM)-матрица, таких, что

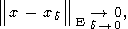(5)

где d есть величина, фигурирующая в (3).

Алгоритмы, основанные на нахождении приближенных решений (4) со свойством (5), именуются регуляризующими или регулярными.^*) Для построения регуляризующих алгоритмов центральное значение имеет оценка абсолютной погрешности приближенного решения, так называемая схема Лаврентьева-Джона [Лисковец, 1981; Морозов, 1987; Танана, 1981]:

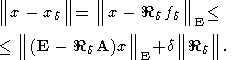(6)

При этом ||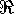|| обозначает произвольную норму матрицы 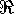, согласованную с эвклидовой нормой векторов, например – эвклидова или спектральная.

Из (6) следует, что (5) будет иметь место, если одновременно будут выполняться соотношения

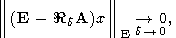(7)

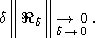(8)

1-3. Исторически первые методы регуляризации задачи нахождения приближенных решений систем (1) по заданным их аппроксимациям (2) были построены для систем с N=M и симметричными положительно полуопределенными матрицами A:

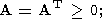(9)

именно, М. М. Лаврентьевым был предложен [Лаврентьев, 1959] метод регуляризации, в случае (9) состоящий в переходе от системы (2) к системе

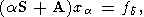(10)

где a = a(d)>0 есть параметр, именуемый параметром регуляризации, а S есть (M M)-матрица со свойством

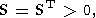(11)

и достаточно хорошо обусловленная. При этом М. М. Лаврентьев [Лаврентьев, 1959] установил регулярность метода, основанного на переходе от (2) к (10), на основе чисто спектральных соображений, не апеллируя к какой-либо вариационной постановке. Однако нетрудно найти, что система (10) возникает при рассмотрении условной экстремальной задачи:

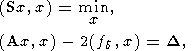(12)

где D - заданная величина. Действительно, условной экстремальной задаче (12) методом множителей Лагранжа ставится в соответствие семейство безусловных экстремальных задач

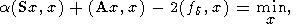(13)

где a>0 - параметр (величина, обратная множителю Лагранжа). Экстремаль задачи (13) как раз и удовлетворяет уравнению (10).

Для нахождения значения параметра регуляризации позже было предложено использовать условие невязки

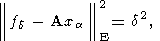(14)

где x_a есть решение уравнения (10). Было доказано, что если

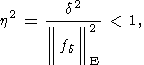(15)

то решение уравнения (14) существует и единственно. Далее А. Н. Тихоновым был предложен метод, ныне именуемый вариационным методом А. Н. Тихонова, который применим к любым системам (2), и который основан на постановке условной вариационной задачи

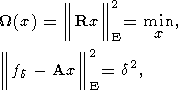(16)

где d² = ||df||²_E - заданная постоянная.

Ясно, что кроме основной экстремальной задачи (16) можно рассматривать и двойственную к ней

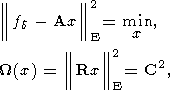(17)

где C² - заданная постоянная. В (16)-(17) R суть заданная матрица, размера P M, где в общем случае P M, которая именуется матрицей-регуляризатором, соответственно функционал W(x) именуется функционалом, задающим отношение предпочтения на множестве приближенных решений системы (2). Последнее означает следующее: если x⁽¹⁾ и x⁽²⁾ суть приближенные решения (2), для которых

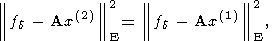(18)

то из неравенства

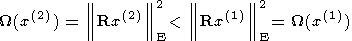(19)

следует, что приближенное решение x⁽²⁾ предпочтительнее приближенного решения x⁽¹⁾. При этом предполагается, что матрица R^T R является невырожденной и достаточно хорошо обусловленной. Подчеркнем, что понятие "функционал, задающий отношение предпочтения на множестве приближенных решений системы (2)", введено В. Н. Страховым, основоположник же метода А. Н. Тихонов именовал функционал W(x) стабилизирующим [Тихонов, Арсенин, 1979]. Соответственно функционал, сопоставляемый любой из условных экстремальных задач (16) и (17),

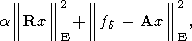(20)

А. Н. Тихонов именовал "сглаживающим параметрическим функционалом", а параметр a>0, фигурирующий в (20) - параметром регуляризации.

Ясно, что в вариационном методе регуляризации решение x = x_a ищется из условия

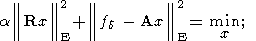(21)

решение x_a существует, единственно и удовлетворяет системе линейных алгебраических уравнений с невырожденной матрицей

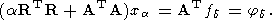(22)

Очевидно, для нахождения значения a и в данном случае может быть использовано уравнение (14), решение которого опять-таки существует и единственно, если выполняется неравенство (15).

Ясно, что величина a>0 является множителем Лагранжа в случае условной вариационной задачи (17), и обратной к множителю Лагранжа - в случае условной вариационной задачи (16).

Заметим, наконец, что уравнение (22) можно рассматривать как регуляризованное по М. М. Лаврентьеву уравнение

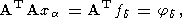(23)

которое возникает в рамках решения классического метода наименьших квадратов, основанного на постановке экстремальной задачи:

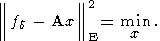(24)

Действительно, при регуляризации по М. М. Лаврентьеву системы (23) достаточно принять

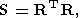(25)

чтобы получить систему (10).

Отметим еще, что в методе наименьших квадратов (24) выполняется характеристическое уравнение этого метода:

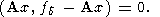(26)

Но в случае регуляризованного уравнения (22) данное соотношение не выполняется. Действительно, имеем

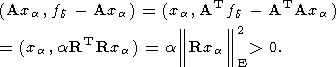(27)

1-4. В рамках классического вариационного метода А. Н. Тихонова возникает система линейных алгебраических уравнений (22) с матрицей размера (MM). Ясно, что в случае систем (2) с N>M это является вполне приемлемым. Однако в случае систем (2) с N<M переходить к регуляризованным системам размера (MN) можно получить, сначала переходя к системе, возникающей при второй трансформации Гаусса исходной системы (2):

(28)

а затем регуляризуя данную систему с симметричной положительно полуопределенной матрицей по М. М. Лаврентьеву:

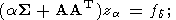(29)

имеем далее

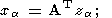(30)

при этом в (29)

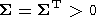(31)

есть достаточно хорошо обусловленная матрица размера (N N). Значение параметра a и в данном случае целесообразно находить из условия (14); решение задачи опять-таки существует и единственно, если выполняется неравенство (15).

Ясно, что матрицу S целесообразно выбирать в виде

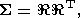(32)

где 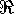есть (NQ)-матрица. Очевидно, 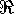также можно трактовать как матрицу-регуляризатор.

Как это не покажется парадоксальным, но конструкция, описанная в данном параграфе - новая.

1-5. Методы, описанные в пп. 1-3 и 1-4, являются наиболее типичными для классической теории регуляризации систем линейных алгебраических уравнений. Но в рамках данной теории были предложены и разработаны (правда, с различной степенью детальности) еще по крайней мере четыре метода:

1) метод, основанный на переходе к так называемой "расширенной регуляризованной системе" линейных алгебраических уравнений;

2) метод, основанный на нахождении сингулярного разложения матрицы A системы (2) и "проекционной регуляризации" [Иванов и др., 1978; Лисковец, 1981; Морозов, 1974];

3) метод итеративной регуляризации, основанный на некотором итерационном процессе - для системы (2), либо (что используется гораздо чаще) для систем (23) или (28), получаемых из (2) с помощью первой или второй трансформаций Гаусса; правило останова процесса в рамках итеративной регуляризации - центральная (регуляризующая) процедура, [см. Алифанов и др., 1998; Иванов и др., 1978; Морозов, 1974, 1987; Танана, 1981; Тихонов и др., 1985];

4) метод, основанный на использовании градиентных процедур поиска минимума квадратичных функционалов, при использовании соответствующего правила останова в процедуре спуска; важнейший частный случай здесь тот, когда применяется метод сопряженных градиентов, см. [Алифанов и др., 1998].

Первый из указанных методов регуляризации будет достаточно подробно описан в следующем разделе настоящей статьи, второй - в следующем параграфе. Что же касается третьего и четвертого методов (точнее - групп методов), то они очень кратко описываются в предпоследнем п. 1-7 данного раздела. Наконец, в заключительном п. 1-8 делаются некоторые дополнительные замечания по основным методам вариационного типа.

1-6. Суть метода проекционной регуляризации в следующем. Пусть A есть (MM)-матрица, и пусть существуют такие ортогональные по столбцам матрицы V и U, размером (NN) и (MM), что:

А) в случае N > M

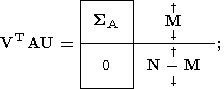(33)

Б) в случае N = M

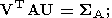(34)

В) в случае N < M

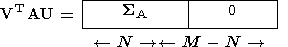(35)

Во всех трех случаях S_A есть диагональная матрица:

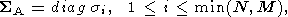(36)

где s_i = s_i( A) суть сингулярные числа матрицы A, упорядоченные по невозрастанию:

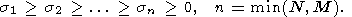(37)

При этом, если A - невырожденная матрица, то s_imax>0, где i_max = min(N, M), в вырожденном же случае s_i>0 только при всех i i₀, 1 i₀< min(N, M).

Очевидно, если даже A невырожденная (в общем случае прямоугольная) матрица, она может быть сколь угодно плохо обусловленной, то есть отношение

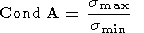(38)

может быть сколь угодно велико.

Итак, пусть сингулярное разложение A найдено, то есть получено одно из трех соотношений - (33), (34), (35), где S_A есть диагональная матрица (36).

Ясно, что в случае (33) получаем систему с диагональной матрицей

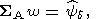(39)

где

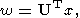(40)

а вектор y_d определен разложением

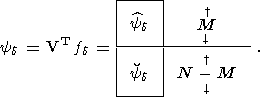(41)

Ясно, что вектор y_d представим в форме

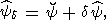(42)

и при этом

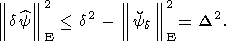(43)

Основная процедура вариационного метода состоит в том, что находится наибольший из номеров i (этот номер обозначается i_гр ) сингулярного числа s_i, такой, что выполняются два неравенства

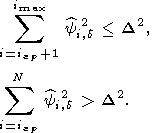(44)

В этом случае принимается

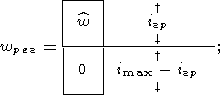(45)

далее используется соотношение

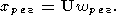(46)

В случаях же (34) и (35) эквивалентная система с диагональной матрицей имеет вид

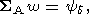(47)

где

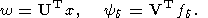(48)

В этом случае опять-таки находится номер i = i_гр, такой, что имеют место неравенства типа (44) - в последних надо только заменить y_i,d на y_i,d, а значение D² на значение d². Дальнейшее, то есть соотношения (45) и (46), остается в силе.

1-7. Метод итеративной регуляризации по существу был разработан уже на начальном этапе развития теории некорректно поставленных задач, в 60-е годы (см., например, работы [Алифанов и др., 1998; Алифанов, Румянцев, 1978, 1980; Бакушинский, 1977; Бакушинский, Страхов, 1968; Вайникко, 1982; Васильев, Якимович, 1980; Гилязов, 1980; Емелин, Красносельский, 1978; Оганесян, Старостенко, 1978; Румянцев, 1985; Рязанцева, 1978; Савр, 1984; Страхов, 1973a, 1973b]). Его суть очень проста. Пусть задан какой-либо итерационный процесс (процесс построения последовательных приближений x⁽ⁿ⁾, n = 0, 1, 2,), относительно которого известно, что в случае точных данных, т.е. системы (1), он сходится к решению этой системы. Тогда этот процесс может быть применен и к системе (2), но с одним отличием - после того, как для некоторого x⁽ⁿ⁾ впервые оказалось

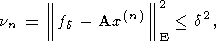(49)

где d² - постоянная, фигурирующая в неравенстве (3) (см. также (14)), итерационный процесс останавливается, и приближение x⁽ⁿ⁾ принимается за искомое. Далее ясно, что поскольку наиболее полно и глубоко теория итерационных процессов разработана для систем с квадратными матрицами A = A^T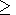 0, то и регуляризованные итерационные процессы (с правилом останова по невязке) чаще всего используются применительно к системам, получаемым из исходной (2) с помощью первой или второй трансформаций Гаусса. На подробностях здесь нет возможности останавливаться.

Аналогичным образом устроены и регуляризованные алгоритмы, в основу которых положены так называемые методы сопряженных направлений (чаще всего - методы A^T A - и AA^T -сопряженных градиентов, [см. Воеводин, Кузнецов, 1984; Марчук, Кузнецов, 1972; Уилкинсон, Райнш, 1976; Фаддеев, Фаддеева, 1963]), а также другие градиентные методы минимизации функционалов. И здесь реализуется та же схема:

1) используемый метод должен обеспечивать сходимость к решению (к одному из решений или псевдорешений) в случае системы (1) с точными данными;

2) в случае системы (2) с приближенными данными регуляризация обеспечивается правилом останова по критерию невязки.

1-8. В заключение раздела остановимся еще на четырех важных вопросах:

во-первых, на вопросе о порядке величины параметра регуляризации a, находимого из уравнения невязки, в случае вариационных методов;

во-вторых, на вопросе о фактическом решении регуляризованных уравнений, возникающих в вариационных методах;

в-третьих, на вопросе регуляризации в ситуации, когда с погрешностью заданы и правая часть, и матрица системы;

в-четвертых, о трудоемкости вариационных методов и путях ее снижения.

Первый вопрос.

Классическое правило А. Н. Тихонова (см. [Иванов и др., 1978; Лисковец, 1981; Морозов, 1974, 1987; Танана, 1981; Тихонов, 1963a; Тихонов, Арсенин, 1979]) для оптимального значения параметра регуляризации a (при котором выполняется уравнение невязки (14)) таково

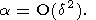(50)

Это правило в дальнейшем было уточнено В. Н. Страховым [Страхов, 1973b]

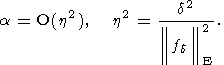(51)

Предлагались и иные правила. Но, по-видимому, наибольшее практическое значение имеет правило В. Н. Страхова, относящееся к случаю, когда спектры помехи и полезного сигнала в существенном разделены:

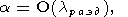(52)

где l_разд - постоянная разделения спектров полезного сигнала и помехи; при этом рассматриваются все три метода - М. М. Лаврентьева (9)-(14), А. Н. Тихонова (18)-(22), (14) и новый метод (28)-(32), (14). Принимается, что l - вещественная переменная, l_i - собственные значения соответствующей симметричной положительно полуопределенной матрицы (A - в методе М. М. Лаврентьева, A^T A - в методе А. Н. Тихонова, AA^T - в новом методе), удовлетворяющие неравенствам:

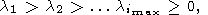(53)

где i_max = M в случае матриц A и A^TA, и i_max = N в случае матрицы AA^T. Если матрица вырожденная, то отличными от нуля являются лишь l_i при ii₀, i₀ < i_max. Пусть Ker(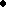) - ядро соответствующей матрицы (A, A^T A, AA^T ), и пусть e_i суть соответствующие ненулевым l_i ортонормированные собственные векторы.

Пусть

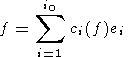(54)

и

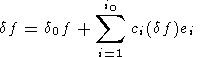(55)

суть разложения полезного сигнала и помехи по ортонормированным собственным векторам e_i, d₀f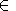 Ker(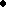). Спектры полезного сигнала и помехи считаются в существенном разделенными, если существует такое число l_i = l_разд, что одновременно выполняются два неравенства:

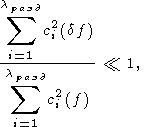(56)

и

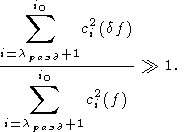(57)

Именно постоянная разделения спектров l_разд, а не величины d² или h², определяют оптимальное значение a в ситуации существенной разделенности спектров полезного сигнала f и помехи df.

Второй вопрос.

Наиболее простой способ найти оптимальное значение a = a_opt и соответствующий вектор x_aopt во всех трех методах вариационного типа (М. М. Лаврентьева, А. Н. Тихонова и новом) состоит в том, что задается последовательность значений a = a_k, k = 1, 2, , k_max, и для каждого из них решается соответствующее регуляризованное уравнение - на основе использования алгоритма Холецкого. Например, в случае уравнения (10) имеем

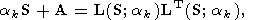(58)

где L( S; a_k) суть нижняя треугольная матрица размера MM. После этого решаются два уравнения с треугольными матрицами

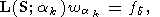(59)

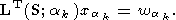(60)

Далее вычисляется величина

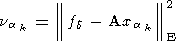(61)

и сравнивается с d². Суть поискового алгоритма очевидна. В случае методов А. Н. Тихонова и нового все обстоит совершенно аналогично.

Третий вопрос.

Итак, пусть для уравнения (1) задана не аппроксимация (2), в которой правая часть задана с погрешностью, а аппроксимация

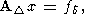(62)

где

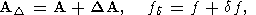(63)

т.е. приближенно заданы и правая часть, и матрица системы.

Ясно, что в этом случае можно использовать все три описанных выше вариационных метода (М. М. Лаврентьева, А. Н. Тихонова и новый), при этом основная проблема состоит в задании оптимального значения параметра a.

С очевидностью имеем неравенство

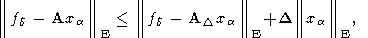(64)

где D определена неравенством

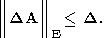(65)

Поэтому оптимальным следует считать то (наибольшее из возможных) значение a, при котором одновременно выполняются два неравенства

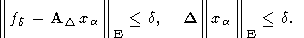(66)

Если подобное значение a не существует, то оптимальным является то, для которого

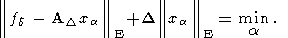(67)

Четвертый вопрос

исключительно важен в связи с тем, что в настоящее время в гравиметрии и магнитометрии остро стоит вопрос о решении систем большой (число неизвестных порядка 10⁴ ) и сверхбольшой (число неизвестных порядка 10⁵ и более) размерности.

Ясно, что наиболее трудоемким является проекционный метод (см. 1-6), основанный на нахождении сингулярного разложения матриц; его трудоемкость оценивается числами арифметических операций, по порядку равными:

(68)

и

(69)

но при этом постоянные, фигурирующие в символах порядка O, как правило весьма велики - 10 и более.

Естественно, что трудоемкость итерационных методов и методов сопряженных направлений (сопряженных градиентов) оценить наиболее трудно - здесь все зависит от спектров полезного сигнала и помехи, а также от выбора начального приближения. Но в целом это наиболее перспективные, с точки зрения их трудоемкости, методы.

Весьма трудоемкими являются все три вариационных метода, но из них привлекательнее всего выглядит метод М. М. Лаврентьева, в котором отсутствует процедура перемножения матриц. Принимая, что при реализации разложения Холецкого используется аккуратный алгоритм счета скалярного произведения (в котором отдельно суммируются положительные и отрицательные частные произведения) и что используется n различных значений a = a_k, найдем, что в главном члене (без учета операций при счете эвклидовых норм невязок) трудоемкость метода составляет

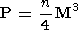(70)

арифметических операций; при этом обычно n колеблется от 24 до 48.

В случае методов А. Н. Тихонова и нового (см. (28)-(32)) к числу P по (70) должны быть добавлены числа операций, затрачиваемых на нахождение произведений матриц:

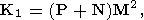(71)

где (P M) – размерность матрицы R, и

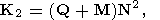(72)

где (N Q) - размерность матрицы .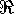

Таким образом, трудоемкость всех вариационных методов достаточно велика, при этом главный источник больших объемов арифметических операций - многократное использование разложений Холецкого - при всех значениях a = a_k, k = 1, 2, , n.

В связи с этим В. В. Воеводиным [Воеводин, 1969; Воеводин, Кунецов, 1984] было предложено - для случая, когда в (10) S = E, в (22) R = E, в (28) 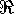= E, использовать операцию приведения основной матрицы (A - в методе М. М. Лаврентьева, A^T A - в методе А. Н. Тихонова, AA^T - в новом методе) к трехдиагональной форме.

Именно, в случае (10) при S = E используется ортогональное преобразование

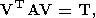(73)

где V - ортогональная по столбцам матрица размера M M, T = T^T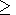 0 - трехдиагональная матрица, и система редуцируется к такой:

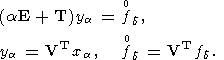(74)

Соответственно в случае (22) при R=E используется аналогичное ортогональное преобразование

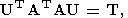(75)

где U - ортогональная по столбцам (M M)-матрица, T = T^T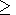 0 - трехдиагональная (M M)-матрица, и система редуцируется к виду

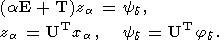(76)

Наконец, в случае (28), (32), при 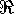= E используется ортогональное преобразование

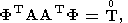(77)

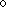где F - ортогональная по столбцам (N N)-матрица, T = T^T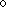 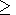0 - трехдиагональная (N N)-матрица, и система редуцируется к виду

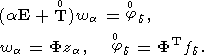(78)

Ясно, что системы с трехдиагональными матрицами решаются очень эффективно, и что числа арифметических операций, затрачиваемых на приведение к трехдиагональной форме, существенно меньше числа P по (70). Однако следует иметь в виду, что при больших значениях N и M, т.е. при большой и сверхбольшой размерности системы, процедуры приведения к трехдиагональному виду не всегда обеспечивают получение необходимой точности - ибо ошибки округления с неизбежностью накапливаются. Поэтому применение приема предварительного приведения к трехдиагональной форме в случае систем большой и сверхбольшой размерности рекомендовано быть не может.

This document was generated by TeXWeb (Win32, v.1.0) on July 4, 1999.