
И. А. Гарагаш
Институт физики Земли РАН
Появление тектономагнитных предвестников связано с изменением напряженного состояния породного массива при сейсмотектоническом процессе. Обычно считается, что формирование локальной геомагнитной вариации на земной поверхности является следствием пьезомагнитного эффекта намагниченных пород [Основы прогноза..., 1983]. Однако пьезоэффект нечуствителен к вариациям интенсивности напряжений и деформаций сдвига (вторых инвариантов соответствующих тензоров). В то же время именно сдвиговые деформации приводят к изменению формы и сопровождают подвижки по разломам.
Причиной возникновения предвестниковых тектономагнитных аномалий может служить взаимодействие деформационных и электромагнитных полей. Развитие этой новой области механики происходило в последние три десятилетия и стимулировалось проблемами, возникающими в геофизике, некоторых разделах оптики и акустики [Knopoff, 1955; Dunkin, Eringen, 1963]. В основе эффекта лежит образование электромагнитного поля в результате деформационного перемещения частиц проводящей среды в магнитном статическом поле. Полная система уравнений, описывающая процесс включает в себя систему квазистатических уравнений электродинамики медленно движущейся среды.
Разработка подхода, основанного на связанности магнитного и деформационного полей представляется перспективным. Согласно известным теориям подготовки очага землетрясения [Мячкин и др., 1975] сейсмическому событию предшествует процесс формирования магистрального разрыва, сопровождаемый сдвиговыми подвижками. Согласно современным представлениям сейсмическое событие рассматривается как процесс локализации сдвиговой деформации. Такой взгляд основан на экспериментах с образцами горных пород [Wawersik, Brace, 1971; Wawersik, Fairhurst, 1979], согласно которым деформирование горных пород сопровождается развитием исходных трещин и образованием новых. При этом эффективные упругие свойства постоянно уменьшаются и наступает разупрочнение материала, выражающееся в реализации нисходящей ветви диаграммы деформирования в условиях контролируемой деформации. После достижения пикового напряжения в характере распределения трещин наступают заметные изменения. Наблюдается появление преимущественной ориентации дефектов в результате частичного закрытия одних из них и ускоренного роста других. Происходит явление известное под названием локализации неупругой деформации [Rice, 1976], которое и завершает разрушение образца. Установленные в лабораторных условиях особенности разрушения материалов с большим числом трещин послужили основой для модели лавинно-неустойчивого трещинообразования (ЛНТ-модель) [Мячкин и др., 1975; Miachkin et al., 1975], одно из основных положений которой состоит в том, что исходная неоднородная среда может быть приведена к некоторой эквивалентной, деформация которой будет будет равна собственно упругой деформации сплошного материала при заданных напряжениях и дополнительной, вызванной наличием дефектов. При этом образование магистрального разрыва (локализация деформации) связано с лавинным развитием внутренней неустойчивости среды, наступающей при критической плотности трещин.
В статье показано, что процесс локализации сдвиговой деформации создает благоприятные условия для появления вариаций магнитного поля в силу эффекта связанности деформационных и электромагнитных полей.
Взаимодействие деформируемого твердого тела с магнитными полями изучалось в геофизике в связи с распространением сейсмических волн. Прежде всего исследователей интересовало как скажутся магнитные эффекты на скоростях сейсмических волн и их затухании. Исследовалось совместное решение уравнений движения магнитного тела [Nowacki, 1976]
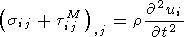 | (1) |
и соотношений
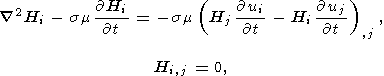 | (2) |
связывающих между собой пространственные и временные изменения компонент вектора напряженности магнитного поля Hi и вектора перемещений ui .
Здесь sij - компоненты тензора напряжений, m - магнитная проницаемость, s - проводимость среды.
Уравнения (1) и (2) являются основными уравнениями магнитоупругости в том случае, когда свободные заряды в теле отсутствуют и токами смещения можно пренебречь. В отличие от обычных уравнения движения (1) содержат магнитный тензор Максвелла
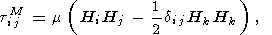 | (3) |
который и обеспечивает влияние магнитного поля на деформации.
В результате решения системы уравнений (1), (2) был сделан вывод [Chadwick, 1956; Knopoff, 1955], что в такой постановке геофизических задач магнитные эффекты малы и учет их не представляет интереса. Однако при поиске предвестников землетрясений речь идет об обратной задаче, когда ищутся весьма малые аномальные изменения магнитного поля, вызываемые механическими движениями среды. Это значит, что мы можем отбросить слагаемое (3) и решить обычную несвязанную задачу о деформациях среды. После чего, подставляя найденные выражения для перемещений в правую часть уравнений (2), можно найти изменения напряженности магнитного поля Hi .
Реализуем изложенный подход для условий локализации деформации в узких зонах. Согласно выражению (2) изменение поля деформации на малую величину ui должно привести к возмущению магнитного поля на величину hi . Поэтому представим величины Hi и Ui в виде сумм
 | (4) |
где H0i , U0i - параметры основного состояния.
Аналогичным образом разделяются и напряжения,
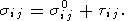 | (5) |
Подставляя (4) и (5) в уравнения (1) и (2) и собирая величины одного порядка малости, получим
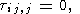 | (6) |
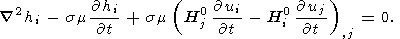 | (7) |
Компоненты напряжений skl связаны с деформациями
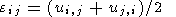 | (8) |
соотношениями
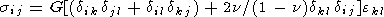 | (9) |
где G - модуль сдвига, n - коэффициент Пуассона.
Поскольку подвижки, предшествующие основному толчку, как было показано выше носят характер локализации деформации, исследуем тектономагнитной эффект именно в связи с этим явлением.
Поле перемещений при образовании полосы сдвига имеет вид [Rice, 1976; Гарагаш, Николаевский, 1989]
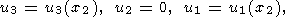 | (10) |
если ось x2 направить препендикулярно полосе, а оси x1 и x3 поместить в ее плоскости (рис. 1).
При образовании зоны локализации деформации внутри нее происходит растрескивание материала, образование блочной структуры и затем катакластическое течение [Miachkin et al., 1975]. Эти процессы приводят к уменьшению эффективного модуля сдвига G в зоне локализации. Для того, чтобы это учесть предствавим модуль сдвига в виде
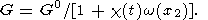 | (11) |
где G0 - модуль сдвига ненарушенного материала, w(x2 ) - функция неоднородности, зависящая как и перемещения только от одной координаты.
 Функция
c(t) характеризует развитие во времени
процесса локализации (рис. 2).
Функция
c(t) характеризует развитие во времени
процесса локализации (рис. 2).
Исходя из того, что в процессе локализации поле напряжений не возмущается [Rice, 1976] и плоскость локализации совпадает с площадкой главного сдвига, из (9) с учетом (11) и (10) получим, что отличные от нуля сдвиговые компоненты возмущенного тензора деформации имеют вид
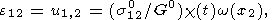 | (12) |
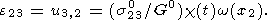 | (13) |
Перемещением нормальным к зоне локализации u2 в дальнейшем пренебрежем в силу его малости по сравнению с перемещениями u2 и u3 в плоскости локализации.
Полагая для определенности, что вектор напряженности магнитного поля H0 лежит в плоскости x1 x2 и составляет угол b с осью x1 (рис. 1), уравнение (7) окончательно преобразуем к виду
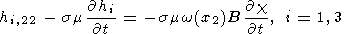 | (14) |
где
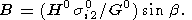 | (15) |
Воспользовавшись преобразованием Фурье, уравнение (14) перепишем в виде
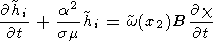 | (16) |
где a - переменная Фурье, h i и w - Фурье-образы функций hi и w соответственно.
Записав решение уравнения (16) и применив к нему обратное преобразование Фурье, получим следующее выражение для hi ,
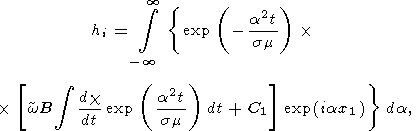 | (17) |
где C1 - постоянная интегрирования.
Определим функцию c следующим образом
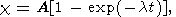 | (18) |
где l - параметр, характеризующий скорость образования полосы локализации.
Функцию неоднородности примем в виде
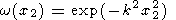 | (19) |
где k - параметр характеризующий полосу локализации.
Производя интегрирование, получим
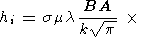 |
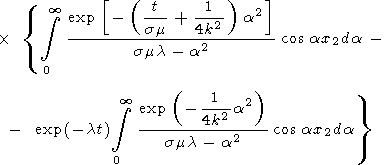 | (20) |
После упрощения уравнения (20) окончательно получим (см. Приложение)
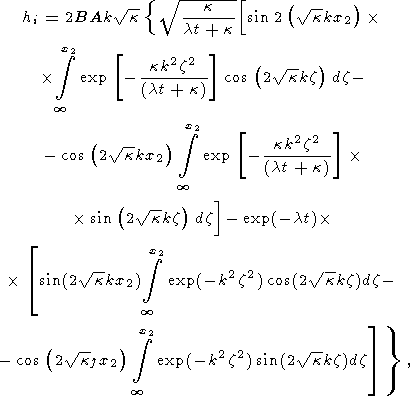 | (21) |
где k = sml 4k2 - безразмерный параметр.
Наибольший эффект должен достигаться на оси зоны локализации x2 = 0. В этом случае формула (20) приобретает вид
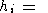 |
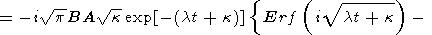 | (22) |
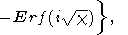 |
где Erf(x) = 2 p x0 exp(- t2)dt - функция ошибки.
 Магнитные свойства горных пород могут колебаться в широких пределах. Так
произведение
sm меняется
от
10-2 до
10-23 сек/м
2 [Rjevskiy, Novik, 1978].
Но учитывая, что
напряженность магнитного поля Земли составляет около 50000 нтл и оценивая
отношение
s0i2/G0
как
10-2 - 10-3 при
A = 1, получаем, что
BA = 1
Магнитные свойства горных пород могут колебаться в широких пределах. Так
произведение
sm меняется
от
10-2 до
10-23 сек/м
2 [Rjevskiy, Novik, 1978].
Но учитывая, что
напряженность магнитного поля Земли составляет около 50000 нтл и оценивая
отношение
s0i2/G0
как
10-2 - 10-3 при
A = 1, получаем, что
BA = 1 500 нтл. Заметим,
что при
A=1 жесткость земной коры на оси полосы сдвига уменьшается в два раза
по сравнению с начальными значениями. Это уменьшение зависит от концентрации
повреждений и микротрещин. Согласно теоретическим [Салганик, 1973]
и экспериментальным
исследованиям [Paterson, 1978] параметр
A может быть и больше единицы. Полагая, что полоса
локализации при подготовке землетрясения может составлять от 1 до
103 м, найдем,
что параметр
k меняется в пределах от 1 до
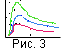
10-4. Построим графики
изменения
hi от
безразмерного времени
lt при значениях
k = 0.01, 0.005, 0.001
и
k = 0.1 m-1,
sm = 10
-3 c/m2,
BA = 300 нтл (рис. 3).
Как видно тектономагнитный эффект довольно
быстро достигает максимума в интервале
0.5
500 нтл. Заметим,
что при
A=1 жесткость земной коры на оси полосы сдвига уменьшается в два раза
по сравнению с начальными значениями. Это уменьшение зависит от концентрации
повреждений и микротрещин. Согласно теоретическим [Салганик, 1973]
и экспериментальным
исследованиям [Paterson, 1978] параметр
A может быть и больше единицы. Полагая, что полоса
локализации при подготовке землетрясения может составлять от 1 до
103 м, найдем,
что параметр
k меняется в пределах от 1 до
10-4. Построим графики
изменения
hi от
безразмерного времени
lt при значениях
k = 0.01, 0.005, 0.001
и
k = 0.1 m-1,
sm = 10
-3 c/m2,
BA = 300 нтл (рис. 3).
Как видно тектономагнитный эффект довольно
быстро достигает максимума в интервале
0.5 lt
lt 2 и затем медленно затухает. При
выбранных реальных параметрах его длительность может составлять десятки минут,
2 и затем медленно затухает. При
выбранных реальных параметрах его длительность может составлять десятки минут,
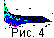 причем при увеличении ширины полосы сдвига это время возрастает. На рис. 4
построена поверхность изменения возмущения напряженности магнитного поля
hi с
течением времени
t в направлении
x2 при
k = 0.1 m
-1,
sm=10-3
c/m
2,
l = 0.04 c
-1,
k = 0.001 и
BA = 300 нтл.
причем при увеличении ширины полосы сдвига это время возрастает. На рис. 4
построена поверхность изменения возмущения напряженности магнитного поля
hi с
течением времени
t в направлении
x2 при
k = 0.1 m
-1,
sm=10-3
c/m
2,
l = 0.04 c
-1,
k = 0.001 и
BA = 300 нтл.
Таким образом выполненный анализ позволяет сделать вывод, что процессы локализации деформации должны сопровождаться заметными вариациями вектора напряженности магнитного поля. При этом эффект существенно зависит от ориентации полосы сдвига по отношениям к вектору магнитного поля Земли и по разному проявляется на разных компонентах. Эти особенности должны учитываться при размещении магнитометров в сейсмоактивных районах. Для получения максимального сигнала надо стремиться ставить их там, где зоны разломов ориентированы под прямым углом к вектору магнитного поля Земли.
Полученное решение может быть использовано для целей прогноза землетрясений. Действительно, тот факт, что согласно уравнению (15) вектор возмущения напряженности магнитного поля hi лежит в плоскости локализации деформации x1 x3 и совпадает с направлением максимального сдвига, позволяет интерпретировать магнитные наблюдения в терминах теории подготовки землетрясения. В спокойные периоды ориентация вектора возмущения в пространстве должна меняться произвольно и соответствовать понятию белый шум. Однако по мере локализации процесса растрескивания и формирования магистрального разрыва следует ожидать появления предпочтительных направлений сдвига и, как следствие, упорядочения ориентации магнитного вектора.
Очевидно, что полученное решение позволяет определить направление подвижки, но не ее плоскость, поскольку фиксируемый в пространстве магнитный вектор принадлежит множеству площадок, для которых он является осью вращения. Чтобы выбрать из этих площадок единственную надо привлечь дополнительные сведения об условиях, в которых происходит локализация. Как отмечалось выше плоскость локализации ориентирована в направлении близком к плоскости максимальных сдвигающих напряжений. Предположим, что одна из компонент вектора максимального сдвига (в нашем случае магнитного вектора) будет совпадать с одним из главных сдвигов. Тогда возникает возможность однозначно определить ориентацию плоскости локализации в пространстве.
Для вычисление интеграла
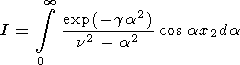 | (A1) |
запишем дифференциальное уравнение
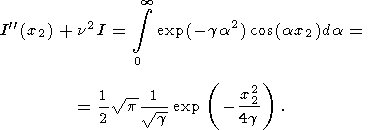 | (A2) |
Используя для решения уравнения (А1) метод вариаций постоянных интегрирования, искомый интеграл представим в виде
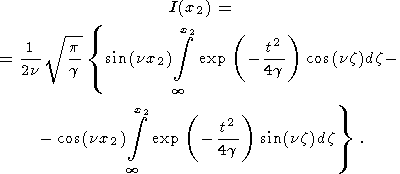 | (A3) |
Гарагаш И. А., Николаевский В. Н., Неассоциированные законы течения и локализация пластической деформации, Успехи механики, 12, в. 1, 131-183, 1989.
Мячкин В. И., Костров Б. В., Соболев Г. А., Шамина О. Г., Основы физики очага и предвестники землетрясений, Физика очага землетрясения, Наука, Москва, 6-29, 1975.
Основы прогноза землетрясений (современное состояние, проблемы и перспективы прогноза землетрясений), Прогноз землетрясений, (3), 220 с., 1983.
Салганик Р. Л., Механика тел с большим числом трещин, Механика твердого тела, Известия АН СССР, 4, 149-158, 1973.
Chadwick, P., Elastic wave propogation in magnetic field, Ninth Int. Congr. Appl. Mech., Brussels, 143-153, 1956.
Dunkin, J. W., Eringen, A. C., On the propagation of waves in an electromagnetic elastic solid, J. Engng. Sci., 1, 461-476, 1963.
Knopoff, L., The interaction between elastic wave motions and a magnetic field in electrical conductors, J. Geoph. Res., 60, 441-457, 1955.
Miachkin, V. I., Brace, W. F., Sobolev G. A., Dieterich J.H. Two models for earthquake forerunners, PAGEOPH, 113, 169-181, 1975.
Nowacki, W., Coupled fields in mechanics of solids, Theoretical and applied mechanics, Proceedings of the 14th IUTAM Congress, Delft, 396-416, 1976.
Paterson, M. S., Experimental rock deformation - the brittle field, Springer-Verlag, 254 p., 1978.
Rice, J. R., The localization of plastic deformation, Theoretical and applied mechanics, Proceedings of the 14th IUTAM Congress, Delft, 439-471, 1976.
Rjevskiy, V. V., Novik, G. I., Physical principles of rocks, Nedra, Moscow, 392 p., 1978.
Wawersik W. R., Brace W. P., Post failure behavior of a granite and diabase, Rock Mechanics, 3, 61-85, 1971.
Wawersik W. R., Fairhurst C., A study of brittle rock fracture in a laboratory compression experiments, Int. J. Rock Mech. Min. Sci., 7, 561-575, 1979.
 |