ЧАСТЬ ПЕРВАЯ

Геомагнитное поле в неогее

Шкала геологического времени

Все характеристики геомагнитного поля и вообще все явления на поверхности Земли так или иначе привязаны ко времени - "датированы". Датировки, выполненные радиологическими методами, имеют глобальный характер, но даже и они "меняются" со временем из-за уточнения констант распада, появления новых и совершенствования старых методов и т.п. Более неопределенны биостратиграфические датировки, нередко имеющие только региональный смысл. Их нужно "привязать" к единой шкале геологического времени. Но шкала геологического времени все время уточняется и в разное время исследований различные палеомагнитные и другие данные привязаны к несколько различающимся шкалам геологического времени. Поэтому для нас важно выбрать шкалу, к которой привязан максимум имеющейся информации и к ней же мы должны привязать все остальные данные. Такой шкалой оказалась одна из последних геохронологическая шкала [Harland et al., 1990], в которую внесены следующие изменения в положении нижних границ в кембрии, венде [Grotzinger et al., 1995] и рифее [Семихатов, Раабен, 1996]: тремадок - 505 Ma, верхний кембрий (разделен далее на два яруса посередине) - 510, средний кембрий (разделен на два яруса посередине) - 520, ботомий - 525, атдабан - 528, томмот - 530, ровенский горизонт (немакит-далдын) - 544, котлинский - 551, редкинский - 570, лапландский (варангер) - 610 Ma; в рифее выделены три эры: верхний рифей - 1050 (разделен на два интервала, граница между ними - 850 Ma), средний рифей - 1350 (разделен на два интервала, граница между ними - 1200 Ma), нижний рифей - 1650 (разделен на два интервала, граница между ними - 1450 Ma).

Предлагаемая схема наверняка небесспорна, но для нашего анализа не так существенна точность каждой из границ (что мы в большой степени "убираем" сглаживанием) гораздо важнее привязка всей информации, как палеомагнитной, так и геологической, к одной шкале геологического времени.

Поведение геомагнитной полярности

Для исследования поведения геомагнитной полярности в течение неогея построена сводная шкала геомагнитной полярности (табл. 1).

Шкала геомагнитной полярности:

1) Для времен, меньших 170 Ма принята шкала из [Harland et al., 1990].

2) Для палеозоя и мезозоя за основу принята магнитостратиграфическая шкала, построенная для территории СССР [Храмов и др., 1982; Molostovsky, Khramov, 1984]; она дополнена и уточнена следующими региональными магнитостратиграфическими данными: а) верхний триас-нижняя юра бассейна Ньюарк [Witte et al., 1991]; б) карбон Северной Америки [Оpdyke, Divenere, 1995]; в) нижний карбон-верхний кембрий Урала [Данукалов и др., 1983]; г) сводная магнитостратиграфическая шкала нижнего и среднего ордовика [Trench et al.,1991]; д) ордовик-верхний кембрий Сибири [Галле, Павлов, 1999; Gallet, Pavlov, 1996; Pavlov, Gallet, 1998]; е) нижний кембрий Восточной Сибири [Kirschvink, Rozanov, 1984].

3) Для венда и рифея использованы а) сводные магнитостратиграфические шкалы венда-рифея Восточной Сибири, Кузнецкого Алатау [Осипова и др., 1988] и среднепротерозойской супергруппы Северной Америки (Монтана и Айдахо) [Elston, Bressler, 1980], которые коррелируют между собой общим видом и по числу инверсий; б) разрез венда Приднестровья [Третяк и др., 1996]; в) часть разреза катавской свиты (верхний рифей) Южного Урала [Комиссарова и др., 1997]; г) разрез вулканитов Мамайнс Пойнт (Кивинаван, средний рифей, возраст от 1109 до 1086 Ma) [Klewin, Berg, 1990]; д) магнитостратиграфический разрез нижнерифейских отложений (примерно 1600-1700 Ma) бассейна Мак-Артур, Австралия [Idnurm, 1992].

Естественно, более древние участки шкалы менее надежны, чем более молодые. Магнитостратиграфические данные нередко не соответствуют современным стандартным требованиям палеомагнитной надежности, что относится не только к работам, выполненным до 1980 года, но и к недавним исследованиям. Нередки случаи, когда приводятся только возрасты границ свит и других крупных подразделений, тогда возраст границ магнитозон оценивается примерно - пропорционально мощности разреза. Так определены, например, возрасты границ магнитозон в разрезе катавской свиты, в нижнекембрийских разрезах Сибири, в разрезе Мамайнс Пойнт, нижнерифейских отложений бассейна Мак-Артур и т.д. В ряде региональных шкал есть пропуски, нерасчлененные интервалы частых смен полярности. Перерывы в шкалах (отсутствие данных) заменены так: если с двух концов такого пропуска магнитная полярность различна, то в середине пропуска проведена граница между магнитозонами, если же полярность по краям пропуска одинакова, то весь пропуск относился к той же полярности. Нерасчлененные интервалы частых смен полярности, встреченные в палеозое, заменены следующим образом. Как будет показано ниже, в мезозое и позднем палеозое основная масса коротких магнитозон имеет продолжительность более 0,25 млн. лет, соответственно, нерасчлененные интервалы частых смен полярности "заполнены" равномерным чередованием магнитозон прямой и обратной полярности с частотой 2-4 инверсии за 1 млн. лет. Сводная шкала привязана к геохронологической шкале (см. выше).

Построенная предлагаемым образом шкала геомагнитной полярности (табл. 1) несомненно имеет недостатки и не пригодна для строгой возрастной корреляции и других подобных магнитостратиграфических задач, вполне возможна неполнота ее, особенно в докембрии. Однако нас интересуют прежде всего глобальные статистические свойства шкалы для выявления крупномасштабных закономерностей и особенностей в поведении геомагнитного поля, для их корреляции с другими крупномасштабными явлениями на Земле.

Следует подчеркнуть, что вряд ли возможно существенно продолжить шкалу геомагнитной полярности в прошлое, поскольку лишь эпизодически удается найти горные породы древнее 2,0 миллиардов лет, которые образуют непрерывные стратиграфические последовательности, не подвергшиеся на протяжении своей геологической истории существенным преобразованиям и сохранившие первичную палеомагнитную информацию.

На основании шкалы геомагнитной полярности анализируются такие характеристики геомагнитного поля как частота инверсий (рис. 1а) и асимметрия полярности (рис. 1в).

Частота инверсий поля.

Для оценки объективности шкалы геомагнитной полярности и построенной по ней картины частоты инверсий относительные изменения знака геомагнитного поля получены и другим способом [McElhinny, 1971] - по соотношению числа индивидуальных палеомагнитных определений (коллекций), включающих обе полярности поля, к общему их числу в данном интервале времени (в нашем случае - 10 млн. лет) (рис. 1б). Такой метод требует большой статистики и даже в этом случае полученный результат является сугубо относительным. Для этого метода мы воспользовались Базой палеомагнитных данных [McElhinny, Lock, 1990, 1993] и результат сравнили с кривой, построенной указанным методом для большей части фанерозоя [Johnson et al., 1995]. Обе кривые практически совпали, хотя несколько отличался подход к отбору данных. Рифейская часть менее надежна из-за больших интервалов, где число палеомагнитных определений менее 4-5 или они вообще отсутствуют.

Картинки поведения знака геомагнитного поля, полученного двумя практически независимыми методами, в фанерозое и венде качественно полностью повторяют друг друга, что позволяет считать объективной картину изменений (цикличности) геомагнитной полярности, во всяком случае в фанерозое и венде. В рифее полученные двумя методами результаты отличаются, что говорит о неполноте картины частоты инверсий в рифее и неполноте рифейской части шкалы геомагнитной полярности [Печерский, 1997]. Например, заметные всплески частоты инверсий в интервалах 750-850 Ма, около 950 Ma и др. (рис. 1б) не сопровождаются заметным повышением частоты инверсий поля (рис. 1а).

Отмеченное сходство частоты инверсий, полученной разными методами, не относится к их количественной характеристике, а именно, к амплитудам колебаний частоты: даже в более надежной кайнозой-позднепалеозойской части шкалы (рис. 1а) размах колебаний "частоты смен полярности поля", определенной вторым методом (рис. 1б), в несколько раз превышает истинную картину. Тем не менее, их синхронность и цикличность в фанерозое-венде позволяет надеяться на объективность совокупной информации и в рифее.

Беглого взгляда на табл. 1 и рис. 1 достаточно, чтобы убедиться, что строение шкалы геомагнитной полярности сильно различается в фанерозое и докембрии: в фанерозое инверсии происходили гораздо чаще, чем в докембрии, в общем, идет нарастание числа инверсий: в среднем одна инверсия происходит через 15,6 млн. лет в рифее, через 1,7 млн. лет - в палеозое, через 1,2 млн. лет - в мезозое и через 0,35 млн. лет - в кайнозое, при этом интервалы длительного отсутствия магнитной полярности распределяются в течение неогея довольно равномерно.

Асимметрия магнитной полярности.

Из симметрии уравнений магнитной гидродинамики следует равноправность обеих полярностей геомагнитного поля. Однако реально (рис. 1в) мы наблюдаем интервалы с различным предпочтением той или иной полярности. При этом асимметрия полярности, построенная для фанерозоя по шкале геомагнитной полярности, совпадает со статистической оценкой асимметрии полярности, определенной по палеомагнитным направлениям каждой коллекции в Базе палеомагнитных данных [Algeo, 1996], что подтверждает объективность картины асимметрии в фанерозое. К сожалению, последним способом построить картину асимметрии геомагнитной полярности для рифея пока невозможно из-за неопределенности полярности многих палеомагнитных определений Базы [McElhinny, Lock, 1990, 1993].

Наблюдаемое сложное поведение асимметрии полярности не находит объяснения в существующих моделях геодинамо. Очевидно, его следует искать вне земного ядра - в мантии, в ее взаимодействии с ядром, во внешних источниках, меняющих режим генерации геомагнитного поля.

На гистограммах продолжительности магнитозон, построенных для ряда интервалов времени (рис. 2), видно, во-первых, общее сходство распределения основной массы магнитозон по продолжительности, все они одномодальные, близкие логарифмически нормальному закону, что говорит о репрезентативности шкал фанерозоя и докембрия. Во-вторых, моды продолжительности магнитозон плавно растут с возрастом, смещаясь от 0,1-0,2 млн. лет в антропогене-миоцене (рис. 2а) до 0,5-1 млн. лет в раннем мезозое-позднем палеозое (рис. 2d, 2e) и далее последняя сохраняется до низов рифея (рис. 2g). Следовательно, преобладающая продолжительность магнитозон 0,2-2,5 млн. лет долго сохраняется в неогее и, начиная с позднего мезозоя, плавно уменьшается до 0,1-0,5 млн. лет. Такое явление невозможно отнести на счет методических погрешностей, так как основное смещение моды приходится на интервал времени, для которого шкала построена методически одинаково - главным образом по линейным магнитным аномалиям океанов (рис. 2а, 2б, 2c). В-третьих, по многим данным [Петрова, 1989; Петрова и др., 1992; Petrova, Pospelova, 1990] известно существование очень коротких эпизодов разной полярности и экскурсов, которые не вошли в шкалы, использованные для построения сводной шкалы неогея. Например, только в субхроне Брюнес таких экскурсов не менее десятка. Соответственно, ожидаемое число магнитозон продолжительностью менее 0,01 млн. лет составит многие десятки и должно образовать отдельную совокупность на гистограмме, т.е. они имеют иную природу. В-четвертых, с рифея до кайнозоя исчезают справа "хвосты" гистограмм: в рифее доля магнитозон продолжительностью более 5 млн. лет составляет 35%, в палеозое - 6%, в позднем мезозое - 2,6%, а в кайнозое они отсутствуют (рис. 2). В-пятых, в течение неогея фиксируются интервалы явно преобладающей и возможно одной полярности, охватывающие десятки миллионов лет (суперхроны и гиперхроны по магнитостратиграфической классификации [Молостовский и др., 1976; Храмов и др., 1982; Molostovsky, Khramov, 1984; Печерский, 1985]. Их "центры" располагаются во времени довольно равномерно (рис. 1а, 1б): 1680, 1520, 1360, 1150, 1100, 900, 700, 630, 470, 290 и 100 Ma, с интервалом 160-200 млн. лет, за исключением двух аномалий между 1150 и 1100 Ma и между 700 и 630 Ma.

Таким образом, учитывая данные об экскурсах и коротких эпизодах, следует говорить, по крайней мере, о трех режимах генерации поля.

В пользу объективности отмеченной картины говорят данные фрактального анализа шкалы [Печерский и др., 1997] (см. ниже).

Фрактальный анализ шкалы инверсий.

На примере шкалы геомагнитной полярности для последних 170 Ма показано, что последовательность инверсий оказывается непериодической (в строгом значении этого термина), случайной последовательностью и обладает фрактальными свойствами [Ермушев и др., 1992; Иванов, 1996; Gaffin, 1989; Merrill, McElhinny, 1983].

В настоящее время существуют достаточно разноречивые результаты численного моделирования на предмет фрактальности последовательности инверсий магнитного поля. Согласно одним моделям решение является периодическим или квазипериодическим, в то время как в других получены ряды инверсий с фрактальными свойствами, близкими к наблюдаемым [Anufriev, Sokoloff, 1994]. Использование длинной шкалы неогея дает возможность более детально изучить ее фрактальные свойства [Печерский и др., 1997].

Характерная особенность шкалы неогея - это существование интервалов постоянной полярности, длительности которых отличаются друг от друга более чем на два порядка (табл. 1). Можно предположить подобие различных временных масштабов, т.е. - фрактальность.

Для изучения фрактальных характеристик шкалы геомагнитной полярности длиной T выделяется некоторый временной интервал D ; N - количество интервалов длиной D на промежутке времени T, в которые попадает хотя бы одна инверсия. В билогарифмическом масштабе (  ln N, lnD ) их зависимость является линейной функцией. Ее угловой коэффициент численно равен фрактальной размерности d. Временные ряды, для которых размерность постоянна и находится в интервале 0,5 < d < 1 в рассматриваемом отрезке времени, являются фрактальными, т.е. обладают самоподобием.

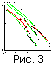В интервале 0-170 Ma выделяются два прямолинейных участка с d₁ 0,5 и d₂ 0,87, излом функции N ( D ) около 2 млн. лет (рис.3, [Иванов, 1996]). С удлинением интервала до 250 Ma (кайнозой+мезозой), где шкала имеет надежность, близкую к первому интервалу, а также для интервала 0-560 Ма (фанерозой), фрактальные характеристики остаются приблизительно теми же, d₁ 0,55 и d₂ 0,83, излом несколько смещается в сторону больших D (рис. 3 [Печерский и др., 1997]). Наконец, для интервала 0-1700 Ма, наряду с первым изломом, появляется второй, при D около 50 млн. лет, в результате выделяются три прямолинейных участка с d₁ 0,55, d₂ 0,66 и d₃ 0,87. Существование второго излома функции N(D) можно объяснить двумя причинами: а) меньшей изученностью докембрийской части шкалы, б) существованием физического процесса с другой фрактальной размерностью. Для проверки первого предположения проведен следующий тест [Печерский и др., 1997]: были отсеяны все интервалы полярности с D<1 млн. лет для всего неогея. И в этом случае (осталось около 20% инверсий) наблюдается излом в том же месте, что и для интервала 0-1700 Ма ( d₁ 0,52 и d₂ 0,88). Поскольку очень маловероятно, что в докембрийской части шкалы неогея пропуски составляют более 80%, то они не могут быть причиной существования второго излома N(D).

Для проверки второго предположения отобраны сравнительно однородные участки шкалы, где инверсии максимально редки. Это интервалы 73-125, 170-370 и 445-1600 Ма и, соответственно, остальные интервалы, представляющие собой участки преимущественно частых инверсий, после чего проведен фрактальный анализ отдельно первого и второго множества. Важно подчеркнуть, что и в первую, и во вторую группы попали участки, как из кайнозойско-мезозойской, так и из менее надежной раннепалеозойско-докембрийской части шкалы. В первом случае наблюдается излом функции N(D) в том же месте, что и в варианте 0-1700 Ма (рис. 3) и те же размерности множеств d₁ 0,56 и d₂ 0,86. Т.е. нет оснований отождествлять фрактальное множество с d<0,6 только с областями частой смены геомагнитной полярности. Во втором случае получена картина, очень близкая варианту 0-170 Ма, с d₁ 0,56 и d₂ 0,9 (рис. 3).

Итак, мы наблюдаем существование трех режимов генерации магнитного поля, выражающихся в наличии трех фрактальных размерностей шкалы инверсий. Другими словами шкала неогея представляет собой наложение трех процессов с фрактальными размерностями d₁ 0,56, d₂ 0,66 и d₃ 0,87. Первый наиболее близок к хаотическому, третий отражает скопления (кластеризацию) частых смен полярностей геомагнитного поля и весьма продолжительные интервалы редких инверсий, что выражается в шкале закономерным чередованием гиперзон частых инверсий (неустойчивое состояние поля) и постоянной полярности (устойчивое состояние поля). При этом режимы с разными фрактальными размерностями накладываются друг на друга ("размазаны" во времени) и возможно вариант с d₂ 0,66 есть результат такого "размазанного" наложения. Это подтверждается как смещением изломов в зависимости от выборки, так и отсутствием каких-либо резких переходов между кривыми N(D) с плавно увеличивающимися временами начала отсчета, а лишь их плавное искривление при увеличении длины ряда [Печерский и др., 1997]. В любом варианте интерпретации результатов фрактального анализа [Иванов, 1996; Печерский и др., 1997; Anufriev, Sokoloff, 1994] последовательность инверсий геомагнитного поля является фрактальной, с размерностью d между 0,5-0,6 и 0,9, что соответствует наблюдаемому распределению инверсий: чередованию областей скопления частых смен полярностей геомагнитного поля с весьма продолжительными интервалами редких инверсий и близкому к хаотическому распределению инверсий при расстояниях между ними менее 2-3 млн. лет [Cox, 1981]. Это происходит на фоне общего нарастания частоты инверсий от раннего рифея к позднему кайнозою, при этом цикличность интервалов длительной постоянной полярности, в общем, сохраняется.

Вейвлет-анализ

В поиске периодичностей какого-либо временного ряда обычно используют фурье-анализ. Однако формальное применение методов фурье-анализа к таким сигналам как геомагнитное поле может приводить к разнообразным артефактам, ложным периодичностям и т.п. Один из путей решения проблемы - это применение вейвлет-анализа, в котором исследуемый сигнал сравнивается не с бесконечной синусоидой, как это делается в анализе Фурье, а с конечным цугом волн. Шкала геомагнитной полярности описывается ступенчатой функцией, фурье-спектр которой включает многочисленные кратные гармоники, вейвлет-анализ не дает кратных гармоник и эффективен при исследовании спектральных свойств непериодических сигналов (см., например, [Holschneider, 1995]).

Вейвлеты представляют собой семейство осциллирующих самоподобных функций различных масштабов, которые локализованы как в физическом, так и в фурье-пространствах. Вейвлет-анализ позволяет изучать нестационарные в спектральном отношении процессы, следить за поведением фазы той или иной составляющей квазипериодического процесса, оценивать его энергетические характеристики. Получаемые при этом спектры являются более гладкими, чем спектры Фурье, в них подавлены кратные и комбинационные частоты. Достоинством вейвлет-анализа является также возможность его применения в случаях временных рядов с пропусками в наблюдениях [Галягин, Фрик, 1996].

Выбор конкретного вида вейвлета зависит от целей анализа. В данном случае [Галягин и др., 1999] применены вейвлеты Морле и "мексиканская шляпа".

Вейвлет-преобразование переводит функцию одной переменной t в плоскость двух переменных t и a. При этом t характеризует положение центра вейвлета на оси времени, а параметр a - временной масштаб осцилляций и в случае использования вейвлета Морле совпадает с периодом колебаний. Аналогом спектра Фурье является так называемый интегральный вейвлет-спектр, получаемый интегрированием квадрата модуля вейвлета вдоль оси времени.

Получен "набор периодов" на интегральном вейвлет-спектре ряда F(t) : 15, 30, 50-60, 70, 100-110, 130, 180, 220, 280 и 390 млн. лет, он принципиально не отличается от ранее получавшегося (см. введение, [Печерский, Нечаева, 1988; Маrzocchi, Mulagria, 1992; McElhinny, 1971; Merrill, McElhinny, 1983 и др.]). В отличие от данных других методов спектрального анализа, по данным вейвлет-анализа мы имеем возможность следить эволюцию спектра во времени. Рассмотрим эволюцию вейвлет-спектра в течение неогея [Галягин и др., 1999] (рис. 4). Во-первых, картина резко различна для фанерозоя-венда и рифея. Во-вторых, внутри венд-фанерозойской области на всем ее протяжении прослеживается колебание с периодом примерно 400 млн. лет, который уменьшается от более 450 млн. лет в венде до менее 400 млн. лет в позднем кайнозое. У остальных более коротких по продолжительности колебаний с периодами от 70 до 200 млн. лет срок жизни гораздо меньший. Так, колебания с периодами 90 и 180 млн. лет прослеживаются от 550 до 200 Ma и оба периода плавно уменьшаются от 200 до 170 и от 100 до 90 млн. лет, соответственно. Период 130 млн. лет устойчив и существует от 180 Ma поныне, причем четкость его заметно нарастает к кайнозою, период 70 млн. лет существует от 160 Ma поныне и уменьшается от 70 до 55 млн. лет. В-третьих, в фанерозое и начале рифея фиксируется серия "всплесков" (примерно 160, 370, 540 и 1650 Ma) на нижней границе вейвлет-плоскости, т.е. их характерные времена около 30 млн. лет.

Устойчивость полученных результатов подтверждается их сходством при проведении вейвлет-анализ с разными окнами сглаживания, от 5 до 30 млн. лет.

Вейвлет-анализ шкалы геомагнитной полярности.

Представляет интерес проанализировать саму шкалу полярности, что можно осуществить с помощью вейвлет-анализа [Галягин и др., 1998, 1999]. Интегральный вейвлет-спектр имеет относительно гладкий вид, на фоне которого наблюдается один выраженный пик ( а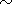 180 млн. лет) и ряд слабых пиков 12, 23, 43, 60, 100, 180, 300 и 600 млн. лет [Галягин и др., 1999]. Картина на вейвлет-плоскости существенно отличается от спектра частоты инверсий (рис. 4). Колебание с периодом 180 млн. лет охватывает интервал 1450-850 Ma. При этом в средней его части период равен 160 млн. лет, а в начале и конце интервала он возрастает до 180-200 млн. лет. Эта структура сменяется в фанерозое довольно устойчивым колебанием, период которого плавно растет от 250 до 300 млн. лет в интервале 450-100 Ma. Остальные "периоды", наблюдаемые на интегральном спектре, обусловлены локальными событиями ("всплесками"). Выделяются три интервала: а) венд-фанерозойский (0-630 млн. лет), внутри которого фиксируются 5 "всплесков", среднее расстояние между ними равно 125 млн. лет; б) середина позднего рифея-середина среднего рифея (860-1260 млн. лет), также 5 "всплесков", среднее расстояние между ними равно 80 млн. лет и в) средний-ранний рифей (1260-1670 Ma), три "всплеска", среднее расстояние между ними 140 млн. лет. Четко фиксируется интервал "молчания" примерно между 850 и 650 Ma (рис. 4).

В общем, вейвлет-плоскости для шкалы геомагнитной полярности и частоты инверсий, по сути, не имеющих ничего общего, подобно отражают разное поведение геомагнитного поля в фанерозое и докембрии [Галягин и др., 1999].

This document was generated by TeXWeb (Win32, v.1.0) on January 11, 1999.