
Б. И. Биргер
Институт физики Земли РАН
Для описания медленных течений в мантии обычно используется реологическая модель степенной неньютоновской жидкости. Однако степенная жидкость в отличие от реального материала не обладает памятью. Новая нелинейная реологическая модель с памятью была недавно предложена автором [Биргер, 1994]. Данная модель сводится к модели степенной жидкости в случае стационарных течений и к модели Андраде в случае течений, вызывающих малые деформации.
Стационарная конвекция под континентами, при исследовании которой используется реологическая модель степенной жидкости [Fleitout, Yuen, 1984], образует верхний холодный неподвижный погранслой (континентальную литосферу). При анализе устойчивости этого слоя следует применять реологическую модель Андраде. Анализ показывает, что литосфера имеет колебательную неустойчивость с периодом колебаний около 200 миллионов лет [Birger, 1995], Эти термоконвективные колебания литосферы рассматриваются в работе [Birger, 1998] как механизм эволюции осадочных бассейнов. Вертикальные движения коры в осадочных бассейнах представляют собой медленные опускания, на которые наложены малоамплитудные колебания. Период колебательных движений коры того же порядка, что и период конвективных колебаний литосферы, найденный при анализе устойчивости. Принимая во внимание значительное различие между темпами седиментации и эрозии, удается объяснить не только колебательные движения в бассейнах, но и медленные постоянные опускания [Birger, 1998].
Анализ конвективной устойчивости горизонтального слоя предполагает рассмотрение возмущений, гармонически зависящих от горизонтальной координаты. Для слоя с реологией Андраде характерна колебательная неустойчивость, и возмущения могут иметь вид как бегущих термоконвективных волн, так и термоконвективных колебаний (стоячих волн) [Birger, 1988]. В настоящей работе будут рассмотрены задачи с различными начальными условиями: мы будем решать линеаризованные уравнения тепловой конвекции для слоя с реологией Андраде при заданных начальных возмущениях температуры.
Линейная наследственная (обладающая памятью) реологическая модель литосферы описывается интегральным соотношением
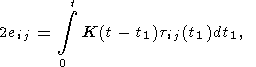 | (1) |
где ei j и ti j девиаторы тензоров деформаций и напряжений, t время, K(t) интегральное ядро ползучести, заданное в виде
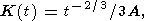 | (2) |
где A реологический параметр Андраде. Ядро ползучести (2) выбрано таким образом, что при постоянном напряжении деформация зависит от времени как t1/3 (закон Андраде).
Уравнения тепловой конвекции для подогреваемого снизу горизонтального слоя выписываются в виде
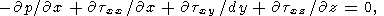 |
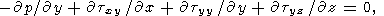 |
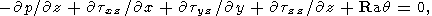 | (3) |
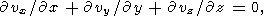 |
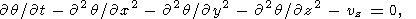 |
где z - вертикальная, а x и y - горизонтальные координаты; v - скорость, q и p - возмущения температуры и давления. Система уравнений (3) записана в безразмерных переменных. В качестве масштаба длины использована толщина слоя d, а в качестве масштаба температуры - разность температур DT между горячей нижней и холодной верхней поверхностями слоя (обе поверхности предполагаются изотермическими). Масштаб времени d2 /k, где k температуропроводность, масштаб скорости k/d. Для ньютоновской вязкой жидкости обычно выбирается масштаб напряжений и давления khd2, а число Рэлея Ra = rgaDTd3 /hk, где r - плотность, a - коэффициент теплового расширения, g - ускорение силы тяжести, h - ньютоновская вязкость, имеющая размерность Па с. Для рассматриваемой реологической среды введем масштабную величину, имеющую размерность вязкости (реологический параметр Андраде A имеет размерность Па с1/3 )
Тогда число Рэлея определено как
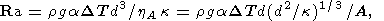 | (4) |
а масштаб напряжений khA d2 = A(d2 / k)-1/3.
Литосфера характеризуется следующими усредненными по глубине значениями физических параметров [Birger, 1995]
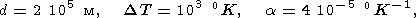 |
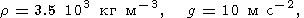 | (5) |
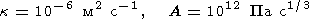 |
Уравнения (3) записаны в приближении Буссинеска. Одним из
условий применимости данного приближения является малость безразмерного
параметра
aDT.
Для литосферы этот параметр оценивается как
aDT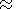 0.04 и действительно может считаться малым. В нулевом
приближении по малому параметру
aDT верхняя
свободно-деформируемая
поверхность слоя, на которой отсутствуют возмущения температуры и
нормальные и касательные напряжения, ведет себя как свободная т.е.
условие обращения в нуль нормальных напряжений заменяется условием
обращения в нуль вертикальной компоненты скорости. Будем считать
нижнюю поверхность слоя также свободной. Тогда граничные условия
на верхней и нижней поверхностях слоя заданы уравнениями
0.04 и действительно может считаться малым. В нулевом
приближении по малому параметру
aDT верхняя
свободно-деформируемая
поверхность слоя, на которой отсутствуют возмущения температуры и
нормальные и касательные напряжения, ведет себя как свободная т.е.
условие обращения в нуль нормальных напряжений заменяется условием
обращения в нуль вертикальной компоненты скорости. Будем считать
нижнюю поверхность слоя также свободной. Тогда граничные условия
на верхней и нижней поверхностях слоя заданы уравнениями
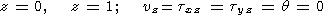 | (6) |
Отметим, что использование свободных граничных условий (6) позволяет найти аналитическое решение задачи, которое не сильно отличается от результатов численных решений, проводимых при более реальных условиях на границах слоя [Birger, 1995, 1998].
Система уравнений (1)-(6) имеет решение в виде конвективной волны
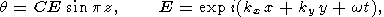 |
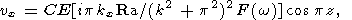 |
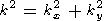 | (7) |
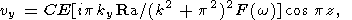 |
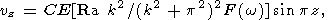 |
где C произвольный комплексный множитель, определяющий амплитуду колебания температуры, kx и ky компоненты волнового вектора (действительные), характеризующие периодичность в горизонтальных направлениях, k волновое число, w комплексная частота (ее мнимая часть описывает затухание волны), F(w) комплексная вязкость, определяемая как
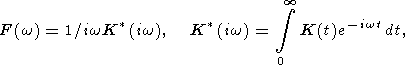 | (8) |
где
K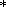 (iw) лапласовское изображение ядра ползучести.
Комплексная частота связана с волновым числом
k дисперсионным
соотношением
(iw) лапласовское изображение ядра ползучести.
Комплексная частота связана с волновым числом
k дисперсионным
соотношением
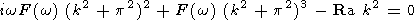 | (9) |
Дисперсионное соотношение (9) позволяет найти такое значение Ram числа Рэлея, называемое минимальным критическим, при котором не затухает только волна c волновым числом k = km и частотой w = wm. Для реологической модели Андраде комплексная вязкость имеет вид
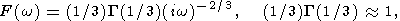 | (10) |
где G(x) гамма-функция, а Ram, km и wm имеют следующие значения
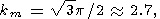 |
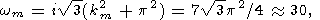 | (11) |
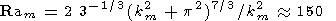 |
Согласно оценкам (5) реологического параметра
A и других физических
параметров литосферы, число Рэлея Ra, характеризующее литосферу
Земли, оказывается того же порядка, что и Ram. Таким образом,
литосфера находится в состоянии, близком режиму пороговой
неустойчивости. Если Ra > Ram, начальные возмущения нарастают со
временем, и при больших
t линеаризованные уравнеия тепловой конвекции
(3), как впрочем и линейное реологическое соотношение (1),
уже нельзя применять. Если же Ra
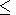 Ram, решение системы уравнений
(1)-(6) при заданных не слишком больших начальных возмущениях температуры
полностью описывает эволюцию возмущений в рассматриваемом
слое, моделирующем литосферу.
Ram, решение системы уравнений
(1)-(6) при заданных не слишком больших начальных возмущениях температуры
полностью описывает эволюцию возмущений в рассматриваемом
слое, моделирующем литосферу.
Решение (7)-(11) получено в нулевом приближении по малому параметру aDT. В этом приближении вертикальное смещение uz верхней поверхности слоя равно нулю. В первом приближении по aDT находим
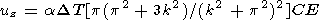 | (12) |
Соотношение (12) не зависит от реологической модели слоя.
Если начальное возмущение температуры в момент t = 0 задано в виде
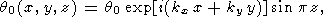 | (13) |
то множитель C в уравнениях (7) и (12) определяется как C = q0. Однако начальное условие (13) не полностью определяет решение задачи об эволюции возмущений. Поскольку в дисперсионное соотношение (9) входит волновое число k, а не компоненты волнового вектора kx и ky, наряду с конвективной волной, описываемой уравнениями (7), имеется решение с волновым вектором (- kx, - ky), которому соответствует волна, бегущая в противоположном направлении. При суперпозиции волн, бегущих в противоположных направлениях, образуется стоячая волна (термоконвективное колебание). Начальному условию (13) удовлетворяют решения исходных уравнений (3)-(6) как в виде бегущих, так и в виде стоячих волн. Неоднозначность устраняется, если вместо начального условия (13) ввести более реальное начальное возмущение, которое охватывает конечную область и обращается в нуль при больших x и y. Такого рода центрированные начальные возмущения будут рассмотрены в четвертом и пятом разделе работы.
В этих разделах работы начальное возмущение задается как
где q0 (x,y) отлично от нуля только в ограниченной области на плоскости xy, а решение ищется в виде
Таким образом, зависимость решения от z фиксирована, и, следовательно, задача о трехмерном распределении возмущения температуры в литосфере сведена к решению двумерной задачи. В случае же, когда начальное возмущение температуры не зависит от y и имеет вид q0 (x), нахождение двумерного распределения температуры сводится к решению одномерной задачи.
Решение в виде конвективной волны справедливо на достаточно больших временах, прошедших с момента возникновения возмущения. Только при этом условии в рассматриваемой реологической модели (1) гармонически зависящие от времени напряжения вызывают деформации, гармонически зависящие от времени, и комплексный аналог вязкости (10) зависит только от частоты, но не от времени.
Когда задано начальное возмущение температуры (13), решение уранений конвекции будем искать в виде
Зависимость возмущения температуры и скоростей от пространственных координат остается такой же, как в соотношениях (7). Задача сводится к нахождению зависимости от времени. Решение ищем при k = km, Ra = Ra m, где значения этих параметров даны формулами (11).
Преобразуя по Лапласу исходные уравнения (1) и (3) и исключая все переменные, кроме температуры, находим лапласовское изображение, соответствующее искомой функции q(t),
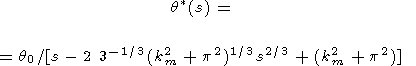 | (14) |
В качестве аналога вязкости теперь выступает функция
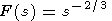 | (15) |
Знаменатель выражения в правой части (14) разложим на множители
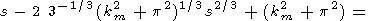 |
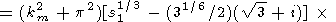 | (16) |
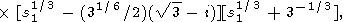 |
где s1 = s/(k2m + p2).
Поскольку
 i)]3 =
i)]3 =  i31/2,
(- 3-1/3)3 = - 1/3,
i31/2,
(- 3-1/3)3 = - 1/3,
можно предположить, что при
s1 = i31/2,
s1 = -i31/2 и
s1 = -1/3 выражение
(16) обращается в нуль. Однако, в выражениях для комплексной
вязкости (10) и (15) подразумевается, что при извлечении корня третьей
степени следует брать только первое значение корня, при котором
аргумент комплексного числа
s удовлетворяет условию
0 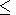 arg s < 2p.
Поэтому
arg s < 2p.
Поэтому
и, следовательно, выражение (16) обращается в нуль при s1 = i31/2, но не равно нулю при s1 = - i31/2 и s1 = - 1/3. Лапласовское изображение (14) удобно переписать в виде
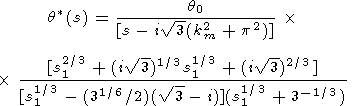 | (17) |
Лапласовское изображение (17) имеет две особые точки: точка ветвления s = 0 и полюс s = i31/2(k2m + p2). В окрестности точки s = 0
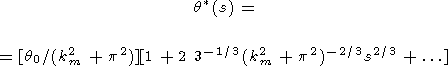 | (18) |
В окрестности точки s = i31/2(k2m + p2)
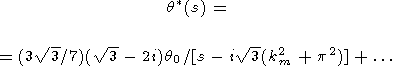 | (19) |
Пользуясь теоремой об асимптотическом поведении оригинала (см., например, [Von Doetsch, 1967]), находим асимптотическое решение, справедливое при достаточно большом t
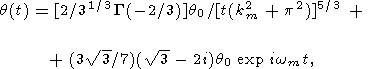 | (20) |
где
wm = 31/2(k2m
+ p2),
что соответствует формуле (11). Первое
непериодическое слагаемое в правой части (20) мало по сравнению со
вторым периодическим слагаемым уже при
t, равном периоду колебания
2p/wm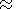 1/5. Таким образом, при
t
1/5. Таким образом, при
t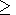 2p/wm решение принимает
вид
2p/wm решение принимает
вид
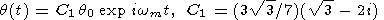 | (21) |
Поскольку
|C1|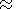 2, амплитуда
установившейся конвективной волны в 2
раза выше, чем начальная амплитуда возмущения температуры
q0.
Аргумент комплексного числа
C1 определяет сдвиг по фазе. В
последующих разделах работы множитель
C1, который появляется
вследствие процесса установления, будем для краткости опускать.
2, амплитуда
установившейся конвективной волны в 2
раза выше, чем начальная амплитуда возмущения температуры
q0.
Аргумент комплексного числа
C1 определяет сдвиг по фазе. В
последующих разделах работы множитель
C1, который появляется
вследствие процесса установления, будем для краткости опускать.
Положив ky = 0, kx = k, будем сначала рассматривать только одномерные возмущения, независящие от координаты y. Разложим комплексную частоту в ряд по степеням k - km
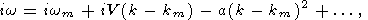 | (22) |
где коэффициент V имеет смысл групповой скорости пакета термоконвективных волн. Подставляя разложение (22) в дисперсионное соотношение (9), находим значения коэффициентов разложения для модели Андраде
Групповая скорость V термоконвективных волн в среде с реологией Андраде несколько ниже, чем фазовая скорость wm / km = 7p/2.
Начальное возмущение температуры q0 (x) представим в виде интеграла Фурье
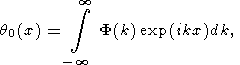 | (23) |
где F (k) изображение Фурье начальной температуры
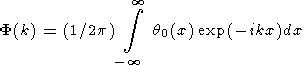 | (24) |
Решение, удовлетворяющее начальному условию, представимо в виде
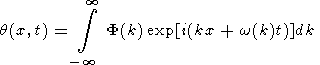 | (25) |
Подставив разложение частоты (22) в (25) и сделав замену k - km = u, получаем
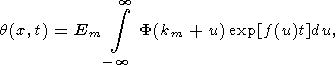 | (26) |
где интегрирование фактически проводится только по малой окрестности точки u = 0 (k = km) и введены обозначения
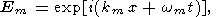 |
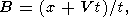 | (27) |
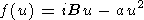 |
Чтобы найти интеграл в правой части (26), воспользуемся методом перевала (см., например, [Copson, 1965]). Стационарная точка u0 (точка перевала) находится из условия
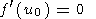 | (28) |
Как следует из формул (27) и (28),
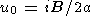 | (29) |
В окрестности точки u0 функция f(u) представима в виде ряда
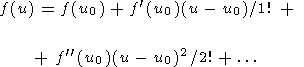 | (30) |
Поскольку f ' (u0) = 0, а f '' (u0) = - 2a, правую часть (30) запишем как
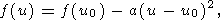 | (31) |
где в правой части сохранены только два первых члена разложения.
Подставляя (31) в (26), получаем
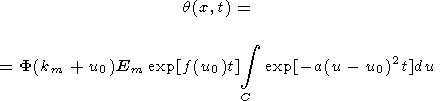 | (32) |
Для функции комплексного переменного f(u) точка u0 является седловой точкой. Согласно методу перевала, мы выбираем контур интегрирования в комплексной плоскости таким образом, чтобы он проходил через седловую точку u0 и в малой окрестности этой точки представлял собой прямую линию, на которой функция f(u) - f(u0) действительна и отрицательна. В окрестности точки u0
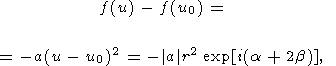 | (33) |
где
a = |a| exp (ia), u - u0 = r exp (ib). Из равенства (33) ясно, что функция f(u) - f(u0) принимает действительные отрицательные значения в окрестности u0, если контур интегрирования представляет собой отрезок прямой, для которой b = -a/2. При таком контуре интегрирования интеграл в формуле (32) преобразуется к простому выражению
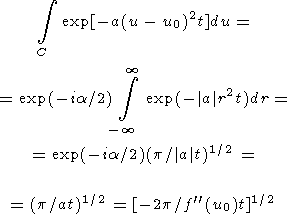 | (34) |
В преобразованиях (34) использована известная формула для интеграла
ошибок, а переход к бесконечным пределам интегрирования законен
при условии
|a| t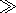 1. Поскольку в использованном
разложении (22)
|a|
1. Поскольку в использованном
разложении (22)
|a|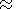 10, полученный результат справедлив
при
t
10, полученный результат справедлив
при
t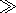 1/10. При этом
условии не нужно учитывать найденную в предыдущем разделе
непериодическую добавку к волновому решению, связанную с процессом
установления.
1/10. При этом
условии не нужно учитывать найденную в предыдущем разделе
непериодическую добавку к волновому решению, связанную с процессом
установления.
Итак решение для произвольного начального возмущения найдено в виде
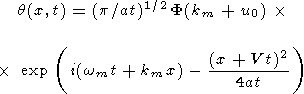 | (35) |
Это волновой пакет, бегущий влево. Для того, чтобы построить полное решение задачи, в правую часть уравнения (35) следует добавить слагаемое, соответствующее волновому числу k = - km. Данное слагаемое получается простым изменением знака перед km и V в правой части равенства (35) и описывает волновой пакет, бегущий вправо.
Переменную
x = x + Vt можно интерпретировать
как координату в
системе отсчета, которая двигается вместе с волновым пакетом с
групповой скоростью
V. Правая часть равенства (35) обращается в
нуль при
x2 /4|a| t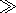 1. Можно считать, что ширина волнового пакета
порядка
2(2|a| t)1/2 т.е. волновой пакет существует
при
|x|
1. Можно считать, что ширина волнового пакета
порядка
2(2|a| t)1/2 т.е. волновой пакет существует
при
|x|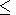 (2|a|
t)1/2. При этом условии из равенства (29) следует
|u0| = |x|/2|a|
t
(2|a|
t)1/2. При этом условии из равенства (29) следует
|u0| = |x|/2|a|
t 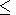 (2|a|t)-1/2.
Отсюда, поскольку
|a| t
(2|a|t)-1/2.
Отсюда, поскольку
|a| t  1, получаем, что
|u0 |
1, получаем, что
|u0 | km,
и, следовательно,
в формуле (35) можно, вместо
F (km +
u0), писать просто
F (km).
km,
и, следовательно,
в формуле (35) можно, вместо
F (km +
u0), писать просто
F (km).
В случае начального точечного возмущения температуры функция q0 (x) и ее изображение Фурье записываются как
 | (36) |
где d (x) - дельта-функция, для которой, как известно,
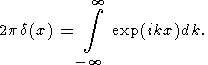 |
Если отказаться от безразмерных переменных, дельта-функция имеет размерность обратной длины, а Q0 - температуры, умноженной на длину.
Как следует из (35), асимптотическое
(|a| t 1) решение в
случае начального возмущения (36) принимает вид
1) решение в
случае начального возмущения (36) принимает вид
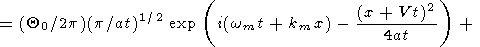 |
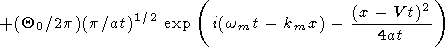 |
Данное решение представляет собой два волновых пакета, разбегающиеся в разные стороны с групповой скоростью V из точки x = 0, в которой произошло начальное возмущение температуры. Распределение температуры в фиксированные моменты времени показано на рис. 1. С течением времени пакеты расплываются: их протяженность увеличивается, а высота (максимальное возмущение температуры) уменьшается.
Пусть начальное возмущение представляет собой два точечных возмущения
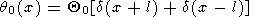 | (37) |
Начальному возмущению (37) соответствует изображение Фурье
но в этой задаче изображение Фурье можно не использовать, поскольку
решение есть просто суперпозиция решений для точечных возмущений
в точках
x=l и
x=-l. Из этих точек разбегаются волновые пакеты.
Их четыре: из точки
x=l - влево и вправо и из
x=-l - влево и
вправо. Пакеты движутся со скоростями
 V. В момент
t0 = l/V центры
двух пакетов, бегущих навстречу друг другу, всречаются в точке
x =0. Обозначим
t1 = t-t0
( t1 положительно после встречи пакетов и
отрицательно до встречи). Возмущение температуры при
-l
V. В момент
t0 = l/V центры
двух пакетов, бегущих навстречу друг другу, всречаются в точке
x =0. Обозначим
t1 = t-t0
( t1 положительно после встречи пакетов и
отрицательно до встречи). Возмущение температуры при
-l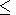 x
x 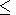 l представляет собой суперпозицию двух волновых пакетов
l представляет собой суперпозицию двух волновых пакетов
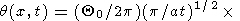 |
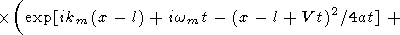 | (38) |
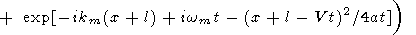 |
Подставляя t = t0+t1 в правую часть (38) и замечая, что
после алгебраических преобразований получаем
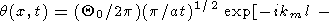 |
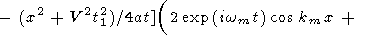 |
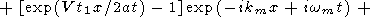 | (39) |
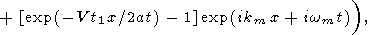 |
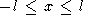 |
Таким образом, формула (39) представляет возмущение температуры в виде суперпозиции стоячей волны и двух бегущих в противоположных направлениях волн. При малых x и t1 амплитуды бегущих волн обращаются в нуль, и в окрестности точки x =0 решение (39) сводится к стоячей волне
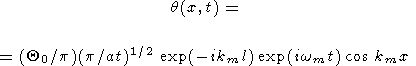 | (40) |
Равенство (40) справедливо при
|x|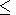 D
x и
|t1|
D
x и
|t1|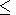 Dt,
где
2Dx - ширина зоны стоячей волны,
2Dt - время существования стоячей
волны. Эти величины оцениваются как
Dt,
где
2Dx - ширина зоны стоячей волны,
2Dt - время существования стоячей
волны. Эти величины оцениваются как
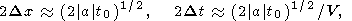 | (41) |
где
|a|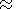 10. Характерному размеру кратона
порядка 2000 км соответствует
l
10. Характерному размеру кратона
порядка 2000 км соответствует
l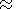 10. Тогда
t0 = l/V
10. Тогда
t0 = l/V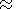 1,
ширина зоны стоячей волны
2Dx
1,
ширина зоны стоячей волны
2Dx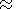 5,
а время существования
2Dt
5,
а время существования
2Dt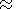 1/2. Поскольку длина волны
2p/km
1/2. Поскольку длина волны
2p/km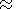 2, а период конвективного колебания
2p/wm
2, а период конвективного колебания
2p/wm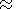 1/5, в зоне стоячей
волны укладываются две длины волны, а за время существования стоячей
волны происходит два периода колебания.
1/5, в зоне стоячей
волны укладываются две длины волны, а за время существования стоячей
волны происходит два периода колебания.
Рассмотрим теперь другой пример начального возмущения
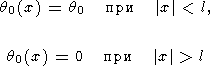 | (42) |
Изображение Фурье для функции (42) запишем в виде
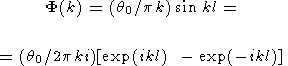 | (43) |
Для изображения (43) решение записывается как
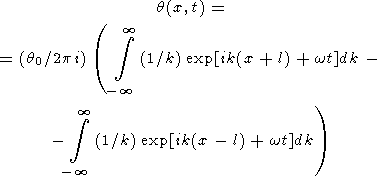 | (44) |
В правой части (44) интегрирование фактически производится только в малых окрестностях точек k = km и k = -km, и это уравнение можно переписать в виде
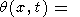 |
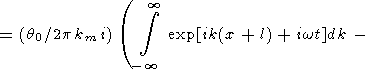 |
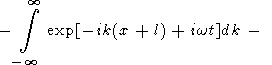 | (45) |
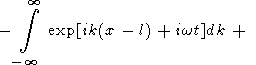 |
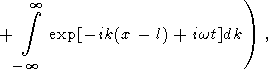 |
где w является функцией k, причем w (km) = wm. Каждый из четырех интегралов описывает волновой пакет, вызванный точечным возмущением. Первый пакет бежит из точки x = -l влево, второй из точки x = -l вправо, третий из x = l влево, четвертый из x = l вправо. Первый и четвертый пакеты бегут из начальной области наружу. Второй и третий пакеты двигаются внутрь начальной области возмущения температуры. Встречаясь, они создают стоячую волну в окрестности x = 0, точно так же как в рассмотренной выше задаче о двух точечных начальных возмущениях.
Рассматривая двумерные возмущения, введем для краткости обозначения kx = p, ky = q. Тогда
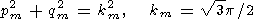 | (46) |
Комплексную частоту w разложим в степенной ряд
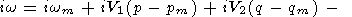 |
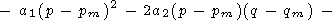 | (47) |
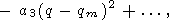 |
где
 |
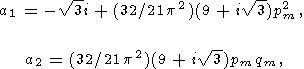 | (48) |
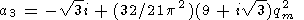 |
Решение, удовлетворяющее начальным условиям, запишем в виде
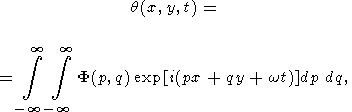 | (49) |
где w = w (p,q), а F (p,q) - изображение Фурье начального распределения температуры q0 (x,y)
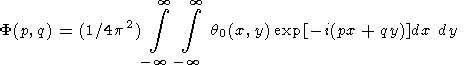 |
Подставляя (47) в (49), получим
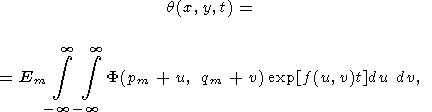 | (50) |
где введены обозначения
Стационарная точка (u0, v0) для функции f(u,v) определяется условием
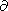 f/
f/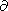 u =
u = 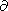 f/
f/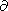 v = 0,
v = 0, с помощью которого находим
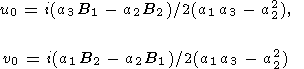 | (51) |
Поскольку
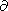 2 f/
2 f/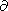 u2 = -2a1,
u2 = -2a1,
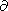 2 f/
2 f/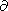 u
u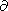 v = -2a2,
v = -2a2,
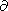 2 f/
2 f/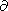 v2 = -2a3,
v2 = -2a3,
в окрестности точки (u0, v0) функция представима в виде
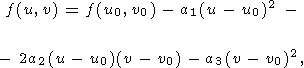 | (52) |
где
Подставляя разложение (52) в (50), получаем
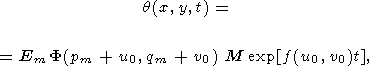 | (53) |
где
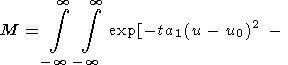 |
Используя замену переменных
представляем M в виде
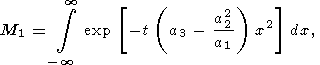 |
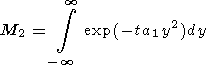 |
Вычисляя интегралы M1 и M2 с помощью метода перевала, преобразуем формулу (53) к виду
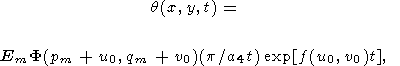 | (54) |
где
Компоненты волнового вектора pm и qm, удовлетворяющие требованию (46), можно представить в виде
 | (55) |
где j изменяется от 0 до 2p. Поскольку все направления волнового вектора (pm, qm) равноправны, в правых частях уравнений (53) и (54) подразумевается еще интегрирование по j.
Если начальное возмущение является точечным,
В формулу (54) следует подставить изображение этой функции
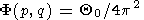 | (56) |
Удобно ввести полярные координаты r и y
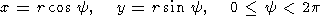 | (57) |
С учетом (55) и (57) множитель Em в правой части (54) имеет вид
Таким образом, температура q при точечном начальном возмущении описывается формулой
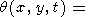 |
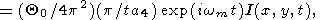 |
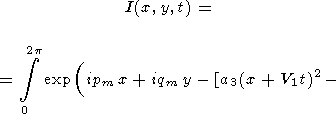 | (58) |
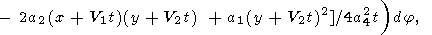 |
где зависимость от j в подинтегральном выражении определяется соотношениями (48) и (55). Поскольку ясно, что q в случае точечного начального возмущения зависит от r, но не от y, можно положить y = 0 (при этом x = r, y = 0 ) в подинтегральном выражении. Тогда
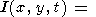 |
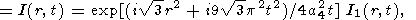 |
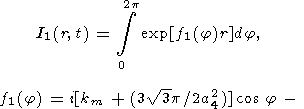 | (59) |
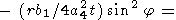 |
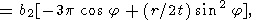 |
где
Значение интеграла I1 (r,t) при больших r находим методом перевала
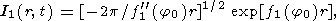 | (60) |
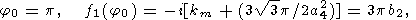 | (61) |

 1
(j0) = i[km
+ (33p/2a24)]-rb1
/2a24 t = b2
[(r/t)-3p]
1
(j0) = i[km
+ (33p/2a24)]-rb1
/2a24 t = b2
[(r/t)-3p] В результате простых алгебраических преобразований получаем асимптотическое (справедливое только при достаточно больших t и r ) решение задачи для начального точечного возмущения температуры
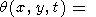 |
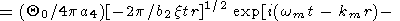 | (62) |
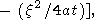 |
где
Отметим, что параметр a уже появлялся в одномерной задаче. Решение (62) описывает цилиндрическую волну, поскольку зависимость от пространственных координат сводится к зависимости только от r = (x2 + y2)1/2.
Функция f1 (j), введенная в формулах (59)-(61), кроме точки перевала j0 = p, имеет точку перевала j0 = 0. Рассмотрение этой точки перевала привело бы к появлению в правой части (62) дополнительного слагаемого, включающего множитель
который обращается в нуль при больших положительных r и t. Данное слагаемое описывает волну, приходящую в точку r = 0 извне, а не волну, возбужденную начальным возмущением температуры в точке r =0.
В центре волнового пакета т.е. при x = 0 (r = 3pt) формула (62) не справедлива. Если x = 0, вторая производная f ''1 (j0) обращается в нуль (равна нулю и третья производная). В этом случае метод перевала, вместо уравнения (60), приводит к равенству
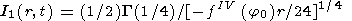 | (63) |
Вывод этого асимптотического соотношения, справедливого при больших r, аналогичен выводу уравнений (30)-(34), но разложение функции в ряд Тейлора проводится до члена, содержащего четвертую производную, а, вместо интеграла ошибок, при выводе используется интеграл
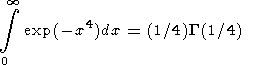 |
Подставляя в (63) значение четвертой производной
находим решение, справедливое в окрестности центра пакета, т.е.
при
r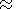 3pt,
3pt,
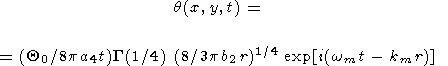 | (64) |
В настоящем разделе применяется упрощенный подход к задачам: не раскладывая w в ряд, просто полагаем, что в уравнении (49) w = wm при значениях k = (p2 + q2)1/2, лежащих в малой окрестности km, а вне этой окрестности подинтегральное выражение обращается в нуль. Тогда
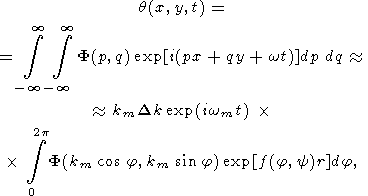 | (65) |
где
Здесь использованы полярные координаты, а интегрирование на
плоскости
p, q проводится по площади кольца, радиус которого равен
km, а его ширина
Dk остается неопределенной величиной в
рамках этого
подхода. На интервале
0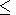 j< 2p
функция
f(j, y)
имеет следующие
стационарные точки
j< 2p
функция
f(j, y)
имеет следующие
стационарные точки
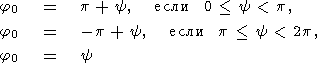 | (66) |
Для точечного начального возмущения температуры (элементарный излучатель термоконвективных волн), подставляя F = Q0 /4p2 в (65), используя метод перевала и отбрасывая решение, соответствующее седловой точке j0 = y (волна, приходящая в точку r = 0 извне) находим решение при достаточно больших r
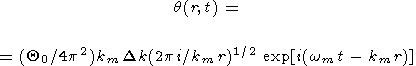 | (67) |
В отличие от полученного выше решения (62), учитывающего зависимость w от волнового числа т.е. дисперсию, уравнение (67) описывает волну с немодулированной амплитудой. Важно, что рассматриваемый простой подход приводит к появлению в уравнении (67) множителя r-1/2, который определяет затухание, характерное для любой (не только термоконвективной) цилиндрической волны (см., например, [Ландау, Лифшиц, 1953]). Сравнивая решение (67) с полученными выше решениями (62) и (64), видим, что для учета дисперсии достаточно подставить в уравнение (67) следующие выражения для Dk
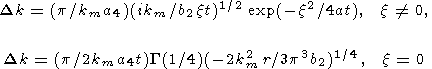 | (68) |
Тот же упрощенный метод будем применять в случае, когда начальное возмущение имеет вид
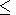 x
x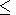 l, -l
l, -l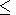 y
y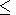 l,
l,
т.е. в начальный момент времени в квадрате со стороной, равной 2l, задано однородное по площади возмущение температуры q0 , а вне квадрата возмущение отсутствует. Для такого начального условия
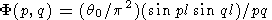 | (69) |
Формулу (69) удобнее записать в виде
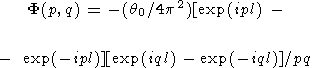 | (70) |
Подставляя (70) в формулу (65), находим
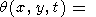 |
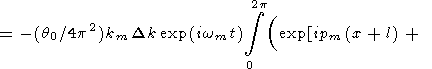 |
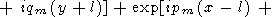 | (71) |
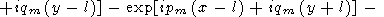 |
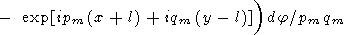 |
Рассмотрим отдельно интеграл, соответствующий первому слагаемому. Вектор (x+l, y+l) соединяет одну из вершин квадрата (-l, -l) с точкой наблюдения (x, y). Введем полярную систему координат с центром в вершине квадрата
 | (72) |
Тогда
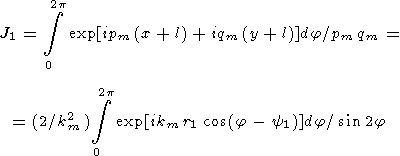 | (73) |
Используя метод перевала и отбрасывая решение, соответствующее волне, приходящей в вершину квадрата извне, получаем выражение для J1 при достаточно больших значениях r1
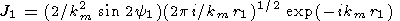 | (74) |
Формула (74) справедлива, когда y1 не находится в малой окрестности точек 0, p/2, p и 3p/2. Подставляя данные значения y1 в (73), нетрудно заметить, что при этих значениях y1 интеграл J1 обращается в нуль в силу симметрии подинтегрального выражения.
Полное решение получается как сумма четырех интегралов в правой части (71)
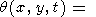 |
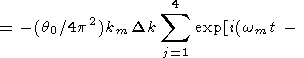 | (75) |
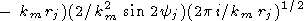 |
В этой формуле углы y3 и y4, соответствующие вершинам квадрата (l, -l) и (-l, l), отсчитываются в обратном направлении (по часовой стрелке). Подставив
 l)2 + (y
l)2 + (y l)2]1/2, yj
= arctg [(y
l)2]1/2, yj
= arctg [(y l)/(x
l)/(x l)],
l)],
 l)2
+ (y
l)2
+ (y l)2]/2(x
l)2]/2(x l)(y
l)(y l),
l), решение (75) можно переписать в виде
где
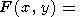 |
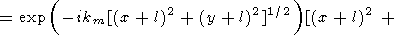 |
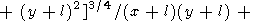 |
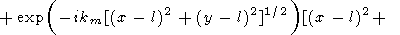 |
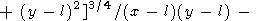 | (76) |
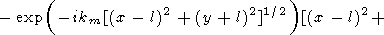 |
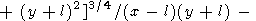 |
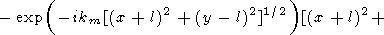 |
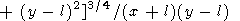 |
Равенство (76) справедливо для всех
x и
y, кроме тех, которые
лежат на линиях
x =  l,
y =
l,
y =  l и в окрестностях этих линий
шириной
порядка длины волны
2p/km.
l и в окрестностях этих линий
шириной
порядка длины волны
2p/km.
Переходя в формуле (76) к полярным координатам
x = r cosy,
y = r siny и используя простое
соотношение, справедливое при
r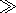 l,
l,
 l)2
+ (y
l)2
+ (y l)2]1/2
= r + l (
l)2]1/2
= r + l ( cosy
cosy siny)
siny)
получаем, что при
r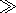 l (на больших расстояниях от начального
квадрата) решение (76) сводится к виду
l (на больших расстояниях от начального
квадрата) решение (76) сводится к виду
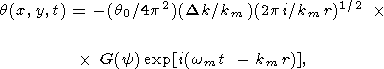 | (77) |
где
Уравнение (77) описывает волну, бегущую из квадрата наружу.
Заметим, что
G, а значит и вся правая часть этого уравнения, не
зависит от
y только при условии
km l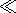 1 (сторона начального квадрата
мала по сравнению с длиной термоконвективной волны). При этом
условии начальный квадрат вырождается в точечное начальное возмущение.
1 (сторона начального квадрата
мала по сравнению с длиной термоконвективной волны). При этом
условии начальный квадрат вырождается в точечное начальное возмущение.
 Графики функции
G(y) построены для различных значений
l на
рис. 2.
Направленность термоконвективного излучения определяется
амплитудным фактором
|G(y)|. Как следует из графиков на рис. 2,
направления наиболее интенсивного излучения:
y = 0,
y = p/2,
y = p,
y = 3p/2. Когда
l
Графики функции
G(y) построены для различных значений
l на
рис. 2.
Направленность термоконвективного излучения определяется
амплитудным фактором
|G(y)|. Как следует из графиков на рис. 2,
направления наиболее интенсивного излучения:
y = 0,
y = p/2,
y = p,
y = 3p/2. Когда
l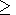 2, действительная функция
G(y) периодически
меняет знак, и, следовательно,
arg G(y) принимает значения 0
или
p. Таким образом, фаза волны, описываемой уравнением
(77),
также зависит от направления.
2, действительная функция
G(y) периодически
меняет знак, и, следовательно,
arg G(y) принимает значения 0
или
p. Таким образом, фаза волны, описываемой уравнением
(77),
также зависит от направления.
В теории излучения простым излучателем называется излучатель,
собственные размеры которого малы по сравнению с излучаемой длиной
волны. Для простых излучателей характерно равномерное излучение во
всех направлениях. Сложный излучатель имеет собственные размеры,
не малые по сравнению с длиной волны, и дает направленное излучение.
Таким образом, начальный квадрат с возмущенной температурой
является простым излучателем термоконвективных волн, если
km l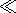 1,
но этот квадрат является сложным излучателем при
km l > 1.
1,
но этот квадрат является сложным излучателем при
km l > 1.
Для того, чтобы учесть дисперсию, которая приводит к модуляции амплитуды (и фазы) волны, достаточно в формулу (77) подставить выражения (68) для Dk.
При
r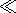 l (в центре начального квадрата)
имеет место
соотношение
l (в центре начального квадрата)
имеет место
соотношение
 l)2
+ (y
l)2
+ (y l)2]1/2
= 21/2l+(1/21/2)r(
l)2]1/2
= 21/2l+(1/21/2)r( cosy
cosy siny),
siny),
где
21/2l расстояние от вершины квадрата до его центра. С учетом
этого приближенного равенства из уравнения (76) следует, что при
r l
l
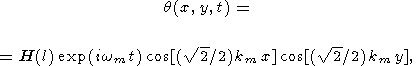 | (78) |
где
Как видно из (78), в центре квадрата
(r l) получается стоячая
волна с квадратными ячейками, стороны которых параллельны осям
координат. Сторона ячейки равна
21/2p/km.
Точно такая же стоячая
волна в окрестности начала координат образуется в случае, когда
начальное возмущение температуры представляет собой четыре точечных
возмущения, расположенных в точках
(l, l),
(l, -l),
(-l, l) и
(-l, -l) т.е. если квадрат начальных возмущений заменяется точечными
возмущениями в его вершинах.
l) получается стоячая
волна с квадратными ячейками, стороны которых параллельны осям
координат. Сторона ячейки равна
21/2p/km.
Точно такая же стоячая
волна в окрестности начала координат образуется в случае, когда
начальное возмущение температуры представляет собой четыре точечных
возмущения, расположенных в точках
(l, l),
(l, -l),
(-l, l) и
(-l, -l) т.е. если квадрат начальных возмущений заменяется точечными
возмущениями в его вершинах.
Отметим, что для получения решения (77), справедливого при
r l, можно использовать формулу (69)
для
F и не разбивать
подинтегральное выражение на четыре слагаемых. Представление
F в виде
(70) понадобилось для построения решения при
r
l, можно использовать формулу (69)
для
F и не разбивать
подинтегральное выражение на четыре слагаемых. Представление
F в виде
(70) понадобилось для построения решения при
r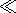 l т.е. в центре
начального квадрата. Применение метода перевала делает полученный
результат (78) справедливым только при условии
km l
l т.е. в центре
начального квадрата. Применение метода перевала делает полученный
результат (78) справедливым только при условии
km l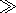 1 (длина
стороны квадрата значительно превосходит длину термоконвективной
волны). Это условие выполняется, когда начальные возмущения
температуры распределены по всему кратону и, следовательно,
l
1 (длина
стороны квадрата значительно превосходит длину термоконвективной
волны). Это условие выполняется, когда начальные возмущения
температуры распределены по всему кратону и, следовательно,
l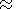 10 при
km = 2.7.
10 при
km = 2.7.
Распределение температуры в литосфере представлено в виде
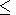 z
z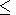 1,
1,
где
q (x,y,t) можно интерпретировать
как возмущение температуры на
срединной плоскости слоя. Найдены возмущения температуры
q (x,y,t),
соответствующие самым простым начальным условиям. Рассмотрены
начальные возмущения
q0 (x,y),
заданные на прямой линии ( x = 0), в
полосе
(-l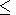 x
x 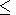 l), в одной точке, в четырех точках и в квадрате.
l), в одной точке, в четырех точках и в квадрате.
Для плоской конвективной волны с волновым вектором (kx, ky) смещение верхней поверхности слоя связано с возмущением температуры соотношением (12). Это соотношение легко обобщается на случай пакета конвективных волн с волновыми числами, близкими km,
Когда рассматриваются более реальные граничные условия на поверхностях литосферы, зависимость возмущения температуры от вертикальной координаты z уже не определяется функцией sin pz, а волновое число km принимает другие (хотя и близкие) значения [Birger, 1998], но по-прежнему смещение uz (x,y,t) равно температуре q (x,y,t), умноженной на некоторую константу, значение которой зависит от выбранных граничных условий. Это справедливо и в том случае, когда постановка задачи учитывает зависимость физических параметров литосферы и, в частности, реологического параметра Андраде от вертикальной координаты z. Таким образом, полученные выше при различных начальных возмущениях функции q (x,y,t) описывают с точностью до множителя вертикальные смещения поверхности литосферы, которые определяют процесс осадконакопления.
Точечные начальные возмущения температуры являются источниками термоконвективных волн в литосфере. Когда начальные возмущения охватывают конечную область, то из этой области наружу разбегаются конвективные волны, а внутри области устанавливаются термоконвективные колебания (стоячие волны). Термоконвективные колебания создают в литосфере систему конвективных ячеек. Над каждой ячейкой поверхность литосферы опускается (или поднимается), образуя осадочные бассейны. Поскольку число Рэлея Ra, характеризующее литосферу, не превышает Ra m, форма ячеек, а следовательно и форма бассейнов, определяется начальными возмущениями. Выше были рассмотрены такие начальные возмущения, которые приводят к квадратным ячейкам. Но при другом выборе начальных возмущений можно получить прямоугольные, гексагональные и другие формы ячеек и бассейнов.
Термоконвективные колебания (стоячие волны) можно рассматривать как механизм, вызывающий образование и эволюцию осадочных бассейнов на континентальных кратонах [Birger, 1998]. В настоящей работе исследована связь конвективных колебаний с начальными возмущениями температуры в литосфере.
Пакеты конвективных волн распространяются в литосфере со
скоростью
3pk/d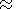 0.15 см/год и создают на верхней поверхности
литосферы прогибания, которые заполняются осадками. Возраст осадков
увеличивается пропорционально расстоянию от переднего фронта волны
до ее источника. Конвективные волны можно связать с известым в
геологии процессом развития переферических прогибов [Белоусов, 1978;
Хаин, 1973]. При
этом процессе внутрь кратона медленно распространяется прогибание,
которое существовало в начальный момент в примыкающей к кратону
геологически активной области ("геосинклинали").
0.15 см/год и создают на верхней поверхности
литосферы прогибания, которые заполняются осадками. Возраст осадков
увеличивается пропорционально расстоянию от переднего фронта волны
до ее источника. Конвективные волны можно связать с известым в
геологии процессом развития переферических прогибов [Белоусов, 1978;
Хаин, 1973]. При
этом процессе внутрь кратона медленно распространяется прогибание,
которое существовало в начальный момент в примыкающей к кратону
геологически активной области ("геосинклинали").
Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант № 97-05-65415.
Белоусов В. В., Эндогенные режимы материков, 232 c., Недра, Москва, 1978.
Биргер Б. И., Реологическая модель мантии Земли и планет земной группы, Теоретические проблемы геодинамики и сейсмологии, C. 42-55, Наука, Москва, 1994, ( Вычисл. сейсмология, Вып. 27).
Ландау Л. Д., Лифшиц Е. М., Механика сплошных сред, 788 c., Наука, Москва, 1953.
Хаин В. Е., Общая геотектоника, 512 c., Недра, Москва, 1973.
Birger, B. I., Linear and weakly nonlinear problems of the theory of thermal convection in the earth's mantle, Physics Earth Planet. Inter., 50, 92-98, 1988.
Birger, B. I., On a thermoconvective mechanism for oscillatory vertical crustal movements, Physics Earth Planet. Inter., 92, 279-291, 1995.
Birger, B. I., Rheology of the Earth and thermoconvective mechanism for sedimentary basins formation, Geophysical Journal International, 134, 1-12, 1998.
Copson, E. T., Asymptotic expansions, University Press, 170 p., Cambridge, 1965.
Fleitout, L., and Yuen, D. A., Steady state, secondary convection beneath lithospheric plates with temperature- and pressure-dependent viscosity, J. Geophys. Res., 89, 9227-9244, 1984.
Von Doetsch, G., Anleitung zum praktischen Gebrauch der Laplace-Transformation und der Z-Transformation, Springer, 365 p., Munchen, 1967.
 |