
В. П. Трубицын, В. В. Рыков
Институт физики Земли им. О. Ю. Шмидта, Российская академия наук
В 70-х годах произошли коренные изменения в представлениях о процессах в недрах Земли и соответственно их проявлений на поверхности. Имея возможность изучить процессы на дне океанов, ученые США и Европы открыли, что океаническая литосфера перемещается в стороны от срединно-океанических хребтов. В хребтах океаническая литосфера рождается при застывании извергающейся магмы, а зонах субдукции остывшие и утяжеленная литосфера затягивается обратно в мантию. При этом вся литосфера Земли разбита на отдельные плиты, часть из которых несет на себе континенты. Эти представления были сформулированы в виде концепции тектоники океанических литосферных плит. Концепцию тектоники литосферных плит понимают не только в этом узком смысле, но и более широком, когда с ней связывают формулировку представлений об основных глобальных процессах в мантии Земли, проявлением которых и является движение литосферных плит.
В эти же 60-70-е годы на основе данных измерения скоростей распространения сейсмических волн и экспериментальных и теоретических данных о свойствах вещества при высоких давлениях были построены первые надежные модели распределения плотности, давления и температуры в Земле.
Плотность растет с глубиной в мантии в основном не за счет изменения химического состава, а за счет сжимаемости и фазовых переходов при росте давления. Температура в мантии очень высока и вещество при длительном воздействии способно течь подобно высоковязкой жидкости. На этом основании был сделан вывод, что в мантии может быть интенсивная тепловая конвекция.
Циркулирующее в мантии вещество при подъеме к поверхности охлаждается и
при температуре порядка
T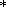 =1300o
C затвердевает, образуя полужесткую
океаническую литосферу. По мере продвижения на горизонтальном участке
конвективной ячейки литосфера еще более охлаждается и утолщается. На
нисходящем участке конвективной ячейки погрузившаяся литосфера еще долго
остается полужесткой до тех пор, пока не нагреется до температуры
T
=1300o
C затвердевает, образуя полужесткую
океаническую литосферу. По мере продвижения на горизонтальном участке
конвективной ячейки литосфера еще более охлаждается и утолщается. На
нисходящем участке конвективной ячейки погрузившаяся литосфера еще долго
остается полужесткой до тех пор, пока не нагреется до температуры
T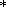 . Таким
образом, океаническая литосфера не плавает на поверхности нижележащей части
мантии, а участвует в конвективном кругообороте вещества всей ячейки мантии и
является той ее частью, которая в данный момент находится при температуре ниже
T
. Таким
образом, океаническая литосфера не плавает на поверхности нижележащей части
мантии, а участвует в конвективном кругообороте вещества всей ячейки мантии и
является той ее частью, которая в данный момент находится при температуре ниже
T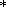 . При этом,
так как горизонтальный размер конвективных ячеек не превышает
20 тыс. км, а максимальная скорость течений порядка 10 см/год, то
возраст
океанической литосферы не может превышать 200 млн. лет.
. При этом,
так как горизонтальный размер конвективных ячеек не превышает
20 тыс. км, а максимальная скорость течений порядка 10 см/год, то
возраст
океанической литосферы не может превышать 200 млн. лет.
Согласно тектоники литосферных плит нет чисто континентальных плит. Континенты считаются всегда вмороженными в океанические плиты и поэтому могут лишь пассивно перемещаться вместе с ними. Благодаря плавучести континенты не могут погружаться в мантию. В отличие от океанической литосферы, толщина которой не превышает 80 км, литосферные корни континентов могут достигать глубин в несколько сот км. Но они не мешают дрейфу континентальных плит, так как вся мантия до ядра ведет себя подобно вязкой жидкости. Следует заметить, что подкоровая литосфера континентов также, как и океаническая литосфера, является областью мантии, отличающейся от остальной мантии лишь реологическими свойствами и в принципе также может перемешиваться конвективными мантийными течениями.
К настоящему времени проведено очень много численных экспериментов для исследования тепловой конвекции в мантии Земли. На двух и трехмерных моделях в декартовой и сферической системе координат выяснена роль переменной вязкости, зависящей от температуры, давления и напряжения и влияние фазовых переходов на структуру мантийных течений. См., например, [Christensen, 1983, 1984; Christensen and Yuen, 1984; Glatzmaier, 1988; Machetel and Weber, 1991; Lenardic and Kaula, 1994; Solheim and Peltier, 1994; Tackley et al., 1994; Parmentier et al., 1994]. В этих моделях было показано, что высоковязкая океаническая литосфера в целом может самосогласованно возникать, если учесть, что вязкость мантийного вещества мантии резко возрастает с температурой особенно вблизи температуры затвердевания [Jacoby and Schmeling, 1982]. Несмотря на большие успехи численного моделирования мантийной конвекции и океанической литосферы как целой, тектоника плит остается не завершенной. Пока не решена основная задача тектоники литосферных плит. Не построено моделей, самосогласованно описывающих разбиение океанической литосферы на отдельные плиты.
Тектоника литосферных плит объясняет процессы возникновения и эволюции только океанической литосферы. Как отмечалось выше, континентальная литосфера обладает существенно отличными свойствами по сравнению с океанической. Она на много толще и время ее существования также на много больше. Утверждение тектоники литосферных плит о том, что нет чисто континентальных плит, относится только к относительно малому интервалу времени, меньшему среднему времени существования океанических плит. За время в 200 млн. лет все океанические плиты погружаются в мантию. Но континенты, хотя могут деформируются, дробится и объединятся, существуют несколько млрд. лет. Поэтому их нельзя рассматривать как пассивные включения в океанические плиты. Если бы континенты дрейфовали пассивно, будучи вмороженными в океанические плиты, то было нельзя также объяснить причины распада суперконтинентов [Trubitsyn and Rykov, 1995].
Свойства океанической литосферы удалось изучить на основе измерения дна океанов. Но континентальная литосфера скрыта под толщей континентальной коры. Поэтому в настоящее время свойства континентальной литосферы исследуются с помощью численного моделирования мантийной конвекции, взаимодействующей с плавающими континентами.
В работе [Трубицын и Фрадков, 1985] впервые было показано, что тепловая конвекция в верхней мантии под континентами подавляется и соответственно\linebreak уменьшается (в три раза) тепловой поток, выходящий через континенты. В то же время океаническая литосфера не может сильно тормозить вынос тепла из мантии, так как океанические литосферные плиты участвуют в конвективном кругообороте вещества мантии. В работах [Трубицын и др., 1991, 1993, 1994; Трубицын и Бобров, 1993; 1996; Lowman and Jarvis, 1993, 1995, 1996; Бобров и Трубицын, 1995; Nakakuki et al., 1997] показано, что неподвижный континент сначала подавляет мантийную конвекцию под собой и расширяет конвективную ячейку, а затем через время в несколько сот миллионов лет, после прогрева субконтинентальной мантии, под континентом возникает горячий восходящий мантийный поток.
Поскольку континенты не фиксированы в пространстве, а плавают по мантии, то их влияние на структуру мантийной конвекции оказывается еще более сильным. В первых работах учитывалось только механическое взаимодействие мантии с движущимися плитами в виде эффективного граничного условия. В местах нахождения плиты условие свободной границы заменялось заданием горизонтальной скорости [Lux et al., 1979; Трубицын и Фрадков, 1986; Doin et al., 1997].
В работе [Gurnis, 1988] приведены результаты расчета численной двумерной модели мантийной конвекции с учетом механического и теплового взаимодействия с плавающими континентами. При этом для предотвращения расплывания вязких континентов был использован искусственный прием фиксации крайних точек континентов. В работах [Trubitsyn and Rykov, 1995; Рыков и Трубицын, 1996a, б] построена первая самосогласованная трехмерная численная модель мантийной конвекции с двумя свободно плавающими трехмерными твердыми континентами на основе прямого решения взаимосвязанной системы уравнений тепловой конвекции и уравнений движения твердых континентов. Эта модель [Trubitsyn and Rykov, 1995] воспроизводит общие закономерности формирования и распада Пангеи. После распада Пангеи образуются структуры подобные Атлантическому и Тихому океанам. При этом на окраинах Тихого океана возникают зоны субдукции с почти вертикальным погружением (типа Курило-Камчатки) на одной окраине и очень пологим погружением (типа Южноамериканской) на другой окраине океана. В работе [Rykov and Trubitsyn, 1996b] при другом начальном положении континентов после распада суперконтинента сформировалась структура двух сцепленных континентов, подобная Северной и Южной Америке.
В работе [Trubitsyn and Rykov, 1997] впервые дано объяснение причины наклонного погружения океанической литосферы под надвигающийся континент. Было проведено самосогласованной численное моделирование конвекции в верхней мантии (при невысоком числе Рэлея Ra=10 4 ) с переменной вязкостью и взаимодействующей с движущимся континентом. Континент моделировался толстой твердой плитой. Рассматривались случаи, когда плита могла свободно плавать в мантии и двигаться с заданной фиксированной скоростью. Оказалось, что при приближении к нисходящему холодному мантийному потоку континент отклоняет его, образуя структуры, подобные наклонным зонам субдукции. Угол наклона от горизонтали для нисходящего мантийного потока растет с ростом скорости надвигающегося континента.
В работе [Трубицын и Рыков, 1998б] на двумерной модели
подробно изложена
математическая постановка задачи и метод ее решения. Рассмотрена более близкая к
реальной Земле модель конвекции при числе Рэлея Ra=10
6 на сетке 200
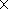 80 с
тонким континентом толщиной
d =90 км и горизонтальным размером
l =6 тыс. км.
Проведены расчеты длительной эволюции системы мантия-континент. Из сравнения
эволюции нестационарной конвекции в мантии без континента и с континентом в те
же моменты времени видно, как движущийся континент кардинально изменяет
структуру мантийной конвекции.
80 с
тонким континентом толщиной
d =90 км и горизонтальным размером
l =6 тыс. км.
Проведены расчеты длительной эволюции системы мантия-континент. Из сравнения
эволюции нестационарной конвекции в мантии без континента и с континентом в те
же моменты времени видно, как движущийся континент кардинально изменяет
структуру мантийной конвекции.
В работе [Трубицын и Рыков, 1998с] на двух и трехмерных моделях представлены результаты серии численных экспериментов, выявляющих четыре особенности тепловой конвекции, проявляющихся в глобальной тектонике Земли. Рассмотрены механизмы возникновения и циркуляции океанической литосферы, генерации и подъема плюмов, характер неполного массообмена между верхней и нижней мантией, влияние плавающих континентов на мантийную конвекцию, в частности создающее различие континентальной и океанической литосферы.
В работе [Трубицын и Рыков, 1998а] сформулирована новая концепция глобальных геодинамических процессов - тектоника плавающих континентов и океанических литосферных плит. Тектоника литосферных плит объяснят процессы под океанами. Тектоника плавающих континентов объясняет процессы под континентами.
В настоящей работе впервые представлена численная модель мантийной конвекции в сферической трехмерной мантии со свободно плавающими континентами.
Как отмечалось во введении, авторами уже в течении ряда лет публикуются результаты моделирования мантийной конвекции, взаимодействующей с плавающими континентами. Оказалось, что именно в результате этого взаимодействия возникают глобальные перестройки мантийной конвекции. Фактически континенты являются регуляторами глобальных геодинамических процессов в Земле [Трубицын и Рыков, 1998а]. Может возникнуть вопрос, почему до сих пор в литературе нет результатов расчета трехмерных моделей мантийной конвекции с плавающими континентами других авторов, хотя эта проблема возникла уже десятилетие тому назад. Причина этого, вероятно, состоит в том, что американские и европейские специалисты по геодинамике полагали континенты менее вязкими, чем океанические литосферные плиты. Но в этом случае они должны деформироваться и раздавливаться быстрее, чем океанические плиты, чего не наблюдается в действительности. Авторы настоящей работы исходили из того, что океаническая литосфера в целом состоит из совокупности плит и может деформироваться и погружаться в мантию легче, чем отдельная плита. Поэтому в качестве первого приближения авторы взяли модель абсолютно твердых континентов, взаимодействующих с мантией. Благодаря зависимости вязкости мантии от температуры и давления маловязкая астеносфера и высоко вязкая океаническая и континентальная литосфера не задаются, а самосогласованно возникают как результат решения уравнений. В результате моделирования континентов твердыми толстыми пластинами и явного использования естественных переменных (скоростей мантийных течений скоростей континентов) оказалось возможным впервые описать не только поступательное движение континентов, но и их вращение в пространстве.
Таким образом, модель сводится к следующему. Рассматривается земной шар, центральная часть которого занимает жидкое ядро, а внешняя оболочка состоит их вязкой силикатной мантии. Граница между ядром и мантией полагается недеформируемой без прилипания и с фиксированной температурой. Для простоты полагается, что подогрев мантии осуществляется снизу. В мантии возникает тепловая конвекция. В мантию погружаются твердые плавучие континенты. На поверхности мантии, не занятой континентами задаются условия свободного проскальзывания для скоростей и нулевая фиксированная температура. На всей поверхности каждого континента задается условия полного прилипания для мантийных течений, а также непрерывность температуры и теплового потока. Таким образом, континент движется под действием полной силы вязкого сцепления с мантийными течениями на торцах и подошве континента. При столкновении континентов во всех местах их соприкосновения вводится эффективная сила отталкивания. Эта сила в каждый момент выбирается из условия, чтобы континенты не пересекались и не отскакивали друг от друга на расстояние, меньшее пространственного шага расчетной сетки.
Тепловая конвекция вязкой мантии описывается распределением вектора конвективных скоростей Vi(x,y,z), распределением температуры T(x,y,z) и давления p(x,y,z). В приближении Буссинеска эти неизвестные функции находятся из решения системы трех уравнений: уравнения переноса импульса, уравнений переноса тепла и массы
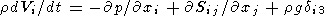 | (1) |
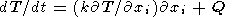 | (2) |
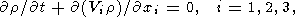 | (3) |
где r - плотность мантии, gi - ускорение силы тяжести, T - температура, отсчитываемая от адиабатического распределения, k - коэффициент теплопроводности, Q - термометрическая плотность тепловых источников, di j - символ Кронеккера, равный 1 при i=j и равный 0 при i j, Si j - девиаторный тензор вязких напряжений [Ландау и Лифшиц, 1986]
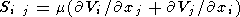 | (4) |
где m - кинематическая вязкость.
Относительная величина инерциальных членов в левой части уравнения
переноса импульс в вязкой жидкости (2) по отношению к членам в правых частях
уравнений имеет порядок
kr/m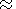 10-23. Поэтому этими
инерциальными членами можно пренебречь. В приближении Буссинеска положим
r = r0(1
- aT) в последнем
члене плавучести уравнения (1) и
r = r0
во всех остальных членах уравнений (1)-(3).
Будем отсчитывать давление от его гидростатического распределения
p(z),
определяемого условием
10-23. Поэтому этими
инерциальными членами можно пренебречь. В приближении Буссинеска положим
r = r0(1
- aT) в последнем
члене плавучести уравнения (1) и
r = r0
во всех остальных членах уравнений (1)-(3).
Будем отсчитывать давление от его гидростатического распределения
p(z),
определяемого условием
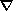 p0 = - r0g.
Введем безразмерные переменные, принимая
за единицу измерения для длины толщину мантии
D, для скорости
D/k, для
времени
D2/k, для температуры
T0, для вязкости
m0,
для давления и напряжений
m0
k/D2,
для плотности тепловых источников
kT0/D2.
p0 = - r0g.
Введем безразмерные переменные, принимая
за единицу измерения для длины толщину мантии
D, для скорости
D/k, для
времени
D2/k, для температуры
T0, для вязкости
m0,
для давления и напряжений
m0
k/D2,
для плотности тепловых источников
kT0/D2.
В этих переменных уравнения конвекции (1)-(3) примут вид
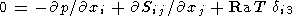 | (5) |
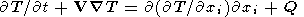 | (6) |
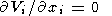 | (7) |
где Ra - число Рэлея, равное
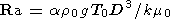 | (8) |
Компоненты скорости любой точки твердого континента u(u, v, w) могут быть представлены в виде [Ландау и Лифшиц, 1965]
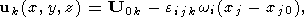 | (9) |
где U0k - вектор мгновенной скорости центра тяжести U0k = (u0, v0, w0) и wi - вектор мгновенной угловой скоростью вращения относительно этого центра тяжести w = (wx, wy, wz), xi - координаты произвольной точки континента, и xi0 - координаты мгновенного центра тяжести континента, eijk - символ Леви-Чивита, равный нулю при совпадении любых двух индексов, равный 1 при четной транспозиции индексов по сравнению с 123 и равный -1 - при нечетной транспозиции.
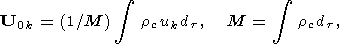 | (10) |
где rc - распределение плотности в континенте, dt - элемент объема, M - масса континента.
Уравнения Эйлера для движения твердого тела в общем случае имеют вид [Ландау и Лифшиц, 1965]
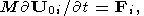 | (11) |
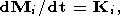 | (12) |
где Fi - внешняя сила, Mi - момент импульса тела.
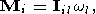 | (13) |
где Iik - тензор моментов инерции тела
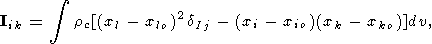 | (14) |
Ki - полный момент силы, складывающийся из моментов ki сил fj, действующих на отдельные элементы тела
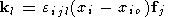 | (15) |
На континент действует сила тяжести, приложенная к центру тяжести, и силы взаимодействия с вязкой мантией, приложенные к элементам поверхности погруженной части континента. Под действием этих сил континент плавает в мантии, перемещаясь вдоль поверхности и вращаясь вокруг вертикальной оси. Так как давление и скорости мантийных течений меняются во времени и в пространстве, то в общем случае не равны нулю как вертикальная скорость центра тяжести континента w0, так и скорости вращения континента wx и wy вокруг мгновенных горизонтальных осей x и y. Континенты могут опускаться (когда они находятся над нисходящими мантийными потоками) вместе с поверхностью мантии и относительно ее и подниматься (в местах восходящих потоков). При этом величина опускания и подъема разных концов континента могут быть разными.
В дальнейшем будем рассматривать только горизонтальные перемещения центра тяжести континента и вращение континента вокруг вертикальной оси, пренебрегая всеми остальными малыми эффектами, полагая w0 = 0 и wx = wy = 0. Поскольку сила тяжести уравновешена выталкивающей силой, то внешняя сила, действующая на континент сводится к силе вязкого сцепления с мантией, при этом давление p нужно считать отсчитанным от гидростатически равновесного распределения p0(z)
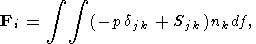 | (16) |
где df - абсолютная величина элемента поверхности твердого континента, nj - единичный вектор внешней нормали к поверхности континента. Интеграл берется по всей поверхности погруженной в мантию части континента произвольной формы.
Таким образом, для горизонтального движения и вращения вокруг мгновенной вертикальной оси твердого континента произвольной формы уравнения Эйлера сводятся к системе трех уравнений [Ландау и Лифшиц, 1965]
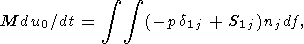 | (17) |
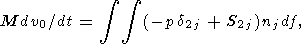 | (18) |
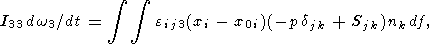 | (19) |
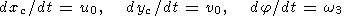 | (20) |
где xc(t) и yc(t) - координаты центра тяжести континента, j - угол поворота континента.
В частном случае при горизонтальном движении твердых бесконечно тонких континентов вязкая сила действует только на подошве континента, для которой nk =(0, 0, -1 ). В этом случае уравнения Эйлера упрощаются
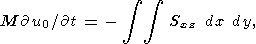 | (21) |
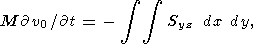 | (22) |
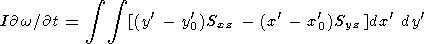 | (23) |
где
I - момент инерции континента относительно оси
z , проходящей
через его центр
тяжести и вычисляемый в подвижной системе координат с осями
x
, проходящей
через его центр
тяжести и вычисляемый в подвижной системе координат с осями
x и
y
и
y ,
направленными по главным осям инерции континента
,
направленными по главным осям инерции континента
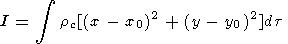 | (24) |
Из соотношений размерности следует, что величина инерциальных членов в
левой части уравнений Эйлера для движения континентов (17-19), как и для
уравнения переноса импульса в вязкой жидкости (1), имеет порядок
kr/m 10-23.
10-23.
После пренебрежения инерциальными членами\linebreak уравнения Эйлера для движения континентов дают шесть соотношений для нахождения шести неизвестных: координат центра тяжести континента xc(t), yc(t), угла его поворота j и скоростей континента u0(t), v0(t) и w3(t)
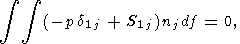 | (25) |
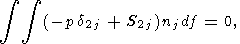 | (26) |
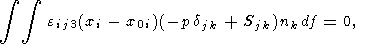 | (27) |
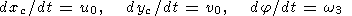 | (28) |
Уравнение для распределения температуры Tc внутри твердого континента в исходной неподвижной системе координат сводится к уравнению теплопроводности с адвективным переносом тепла со скоростями, удовлетворяющими соотношению (9)
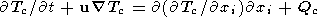 | (29) |
где Qc - плотность тепловых источников внутри континента.
Уравнения мантийной конвекции (1-3) и уравнения для движения континента (17-19) и переноса тепла в нем (29) связаны между собой через граничные условия.
Как указывалось, для мантийных течений на нижней и боковых границах расчетной области принимается условие непротекания и проскальзывания (равенство нулю нормальной составляющей скорости жидкости и равенства нулю тангенциальных составляющих вязких сил)
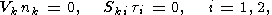 | (30) |
где nk - единичный вектор, нормальный к данной поверхности и ti - единичные вектора, касательные к ней.
На границе твердых движущихся континентов принимается условие непротекания и прилипания, то есть равенство скоростей жидкой мантии и скоростей континента
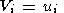 | (31) |
на всей поверхности погруженной в мантию части континента.
Температуры на нижней границе области фиксирована T = 1. На боковых границах принимается условие нулевого теплового потока
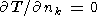 | (32) |
где nk - единичный вектор, нормальный к боковой поверхности области.
На верхней свободной поверхности температура мантии равна нулю ( T = 0) только в океанической области вне континента.
На поверхности погруженной в мантию части континента принимается условие непрерывности температуры и теплового потока между мантией и континентом
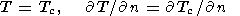 | (33) |
На верхней поверхности континента температура полагается равной нулю
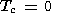 | (34) |
Таким образом, математическая проблема сводится к следующему. Имеется три неизвестные функции координат и времени для мантийной конвекции: вектор скоростей мантийных течений Vi(x,y,z,t), распределение температуры T(x,y,z,t) и распределение давления p(x,y,z,t), а также четыре неизвестные функции времени для движения континентов как целых: две компоненты мгновенной скорости поступательного движения центра тяжести u0(t) и v0(t), одна компонента мгновенной угловой скорости вращения континента вокруг центра тяжести w(t) и распределение температуры в континенте Tc(x,y,z,t). Для их нахождения имеется система взаимосвязанных уравнений: три дифференциальных уравнения конвекции (1-3), три интегральных соотношения (25-27), к которым свелись уравнения Эйлера и уравнение переноса тепла в континенте (29). Зная в данный момент положение и скорости континента u0(t), v0(t) и w(t), можно по (28) найти его положение в следующий момент времени. Для определения постоянных интегрирования дифференциальных уравнений служат граничные условия (30-34).
Отличие рассматриваемой задачи со свободно плавающим континентом от известной задачи с неподвижным континентом состоит в том, что граничные условия для скоростей течений и температуры на границе с континентом ставятся в месте нахождения в данный каждый момент плавающего континента, скорость и положение которого заранее не известны, а определяются из решения системы взаимосвязанных дифференциальных уравнений.
Если континентов несколько, то уравнения движения (25-27) и уравнение для температуры (29) выписываются для каждого континента. Кроме того, при столкновении твердых континентов ставится условия невозможности их проникновения друг в друга. Для этого в моменты соприкосновения континентов в какой-либо точке к силам вязкого сцепления с мантией к каждому континенту добавляется сила расталкивания континентов, приложенная в месте их касания и направленная противоположно относительной скорости континентов. Алгоритм расчета этих сил описан ниже.
При численном решении системы уравнений тепловой конвекции с плавающими континентами можно воспользоваться двумя принципиально различными методами. В методе двух областей на каждом временном шаге отдельно решаются уравнения тепломассопереноса в мантии вне континента и внутри континента, а затем решения "сшиваются", чтобы удовлетворить граничным условиям на погруженной в мантию части континента. В методе сквозного счета на каждом временном шаге при заданном положении континента рассматривается своя единая расчетная область, но на поверхности континента явно учитывается скачек параметров, характеризующих различающиеся между собой свойства вещества мантии и континентов. В методе сквозного счета процедура численного алгоритма более проста, но при этом необходимо проводить сглаживание скачков функций, заменяя на каждом временном шаге твердый континент высоковязкой областью.
В общем виде алгоритм численного счета системы уравнений тепловой конвекции с плавающим континентом сводится к следующему. Пусть в некоторый момент времени t1 нам известны скорости конвективных течений, поле температур T(t1) и давлений p(t1) в мантии, а также положение x1(t1), y1(t1) и скорости континента u0(t1), v0(t1) и w (t1). Нам нужно найти решение системы уравнений (1-5, 25-27 и 29) в следующий момент времени t2 = t1 + Dt. Новое положение континента x1(t2), y1(t2) в момент t2 можно просто найти по (28) x1(t2) = x1(t1) + u0(t1)Dt, y1(t2) = y1(t1) + v0(t1)Dt. Если бы были известны также и новые скорости континента в этом положении u0(t2), v0(t2) и w (t2), то можно было бы снова решить уравнения тепловой конвекции (1-5) с граничными условиями для температуры (32-34) и скоростей (30-31), соответствующими новому положению континента, и найти скорости мантийных течений Vx(t2), Vy(t2) и Vz(t2), температуру T(t2) и давление p(t2) в момент времени t2. Но сложность задачи как раз и состоит в том, что именно эта скорости континента u0(t2), v0(t2) и w (t2) неизвестны. Они должны быть такими, чтобы новые найденные скорости мантийных течений Vx(t2), Vy(t2) и Vz(t2), соответствующие этим новым скоростям u0(t2), v0(t2) и w(t2), удовлетворяли бы также уравнениям движения континента (25-27). Поэтому необходимо найти какой-либо итерационный способ нахождения этих скоростей континента. В принципе можно просто по определенной схеме перебирать значения скоростей континента, рассчитывая поля конвективных скоростей и вычисляя интегралы (25-27), пока не найдутся такие значения u0(t2), v0(t2) и w(t2), при которых правые части соотношений (25-27) отличаются он нуля на значение, меньшее наперед заданного числа e, соответствующего заданной точности счета. Так как по физическому смыслу правая часть соотношений (25-27) соответствуют силам и моменту силы, действующих на континент, то e>0, если выбранная скорости континента u0(t2), v0(t2) и w(t2) занижены и e<0, если они завышены.
Как указывалось выше при расчете движения континентов принимается
условие невозможности их взаимного проникновения. Это условие реализуется
следующим алгоритмом. При расчете движения континентов постоянно проверяется
условие неперекрытия континентов. Если в какой-либо момент
t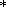 1
некоторая точка
одного континента попала в область другого континента, то расчет возвращается на
предыдущий момент времени
t
1
некоторая точка
одного континента попала в область другого континента, то расчет возвращается на
предыдущий момент времени
t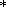 2
= t
2
= t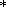 1
- Dt и счет опять возвращается на
предыдущий момент начиная с момента времени
t
1
- Dt и счет опять возвращается на
предыдущий момент начиная с момента времени
t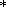
 2,
в правую часть уравнение
движения континента (27-29) добавляется сила расталкивания континентов. Ее
направление, величина и точка приложения выбирается следующим способом.
Сначала определяются средние скорости
U1 и
U2 точек каждого континента,
попавших в область перекрытия другого континента. Затем находится разность этих
скоростей. За точку приложения сил к каждому континенту выбирается центр
области перекрытия. Направление сил расталкивания континентов берется
противоположным относительной скорости одного континента по отношению к
другому. Величина сил отталкивания выбирается итерационным способом. Сначала
берется некоторое значение силы отталкивания и продолжается решение системы
уравнений тепловой конвекции (1-5), переноса тепла в континентах (29) и
уравнений движения континентов (25-27) с учетом этой дополнительной силы
отталкивания. Если же за интервал времени
Dt континенты расходятся на
расстояние, большее шага расчетной сетки, выбранное значение силы отталкивания
уменьшается. В течение времени, когда континенты соприкасаются существенно
изменяются скорости их поступательного и вращательного движения по сравнению
со свободно плавающими континентами.
2,
в правую часть уравнение
движения континента (27-29) добавляется сила расталкивания континентов. Ее
направление, величина и точка приложения выбирается следующим способом.
Сначала определяются средние скорости
U1 и
U2 точек каждого континента,
попавших в область перекрытия другого континента. Затем находится разность этих
скоростей. За точку приложения сил к каждому континенту выбирается центр
области перекрытия. Направление сил расталкивания континентов берется
противоположным относительной скорости одного континента по отношению к
другому. Величина сил отталкивания выбирается итерационным способом. Сначала
берется некоторое значение силы отталкивания и продолжается решение системы
уравнений тепловой конвекции (1-5), переноса тепла в континентах (29) и
уравнений движения континентов (25-27) с учетом этой дополнительной силы
отталкивания. Если же за интервал времени
Dt континенты расходятся на
расстояние, большее шага расчетной сетки, выбранное значение силы отталкивания
уменьшается. В течение времени, когда континенты соприкасаются существенно
изменяются скорости их поступательного и вращательного движения по сравнению
со свободно плавающими континентами.
Решение системы уравнений тепловой конвекции с плавающими континентами проводилось методом конечных разностей [Rykov and Trubitsyn, 1996b]. При численном решении уравнения переноса температуры (6, 29) использовался метод переноса с коррекцией потоков Залесака [Zalesak, 1979]. Уравнения для скоростей и давления (5, 7, 25-28) сводились к уравнениям эллиптического типа с переменными коэффициентами (обобщенным уравнениям Пуассона). Для их решения использовался попеременно треугольный метод в трехслойной модификации с выбором итерационных параметров по методу сопряженных градиентов [Samarskii and Nikolaev, 1978].
Расчеты проводились на трехмерных сферических моделях. Поэтому обсуждаемые выше общие уравнения переписывались в сферической системе координат для искомых скоростей мантийных течений Vr(r, q, f, t), Vq(r, q, f, t), Vf(r, q, f, t), температуры T(r, q, f, t) и скоростей центров тяжестей континентов uq(r, q, f, t), uf(r, q, f, t) и их твердотельного вращения с угловыми скоростями dj/dt в локальной мгновенной сферической системе координат.
Для анализа взаимодействия дрейфующих континентов с мантийными течениями были рассмотрены две модели: модель 1. С одним свободно плавающим континентом при слабой тепловой конвекции в мантии с числом Рэлея при Ra =104 и модель 2. С пятью плавающими континентами при интенсивной конвекции с числом Рэлея Ra=106. Для обеих моделей в качестве граничных условий взята фиксированная температура на границе с ядром и нулевая температура на поверхности. В качестве начального состояния взята вязкая мантия без конвекции с распределением температуры, соответствующим стационарному кондуктивному тепловому потоку. Затем вводилось малое произвольное возмущением температуры и по уравнениям мантийной конвекции рассчитывалась эволюция температуры и скоростей конвективных течений. С течением времени в мантии устанавливалась квазистационарная тепловая конвекция, структура которой практически не зависит от начального возмущения. Затем в мантию помещались континенты и на основе решения системы взаимосвязанных уравнений мантийной конвекции и движения континентов рассчитывалась дальнейшая эволюция системы мантия-континенты.
 Как указывалось выше структура мантийной конвекции в безразмерных переменных при
постоянной вязкости определяется всего одним параметром - числом Рэлея. Для сферической
Земли число Рэлея по различным оценкам, примерно, равно Ra =106. При меньшей интенсивности
конвекция в мантии менее хаотичная и движение континентов более регулярно. Чтобы выявить
особенности дрейфа континентов сначала была рассчитана модель 1.
На рис. 1 приведены
распределения вдоль радиуса для нададиабатической температуры T(r) и числа Нуссельта
Nu=Nu(r) - безразмерного теплового потока, устанавливающихся при конвекции в мантии
при числе Рэлея Ra =104. На рис. 2 показано распределение температуры T(r,q) в сечении
для нулевой долготы. Значения безразмерной температуры в интервале от нуля (на поверхности)
до единицы (на границе с ядром). Соответствие значений температуры и цветовой гаммы указано
в левой части рисунка. Жидкое ядро Земли указано темно-красным цветом. Стрелками указано
направление и относительная величина скоростей мантийных течений. Масштаб безразмерной
скорости также приведен в левой части рисунка. В верхней левой части рисунка указано
значение безразмерного времени, в которое установилась конвекции. В этот момент в
мантию помещен континент, указанный красным цветом в правой части сферы.
Как указывалось выше структура мантийной конвекции в безразмерных переменных при
постоянной вязкости определяется всего одним параметром - числом Рэлея. Для сферической
Земли число Рэлея по различным оценкам, примерно, равно Ra =106. При меньшей интенсивности
конвекция в мантии менее хаотичная и движение континентов более регулярно. Чтобы выявить
особенности дрейфа континентов сначала была рассчитана модель 1.
На рис. 1 приведены
распределения вдоль радиуса для нададиабатической температуры T(r) и числа Нуссельта
Nu=Nu(r) - безразмерного теплового потока, устанавливающихся при конвекции в мантии
при числе Рэлея Ra =104. На рис. 2 показано распределение температуры T(r,q) в сечении
для нулевой долготы. Значения безразмерной температуры в интервале от нуля (на поверхности)
до единицы (на границе с ядром). Соответствие значений температуры и цветовой гаммы указано
в левой части рисунка. Жидкое ядро Земли указано темно-красным цветом. Стрелками указано
направление и относительная величина скоростей мантийных течений. Масштаб безразмерной
скорости также приведен в левой части рисунка. В верхней левой части рисунка указано
значение безразмерного времени, в которое установилась конвекции. В этот момент в
мантию помещен континент, указанный красным цветом в правой части сферы.
 На рис. 3 (7 кадров) приведены результаты расчета эволюции
системы мантия-континент.
Форма континента и его положение для определенности выбраны подобными современной Африке.
Но структура мантийной конвекции не может соответствовать современной Земле, так состояние
мантийной конвекции в момент помещения континента выбрано произвольно. Таким образом,
рассматриваемая модель служит лишь для выявления принципиальной возможности дрейфа континента
и его закономерностей. Цветом указано распределение вычисленного безразмерного теплового
потока (числа Нуссельта) вдоль поверхности Земли. Напомним, что температура на поверхности
континента и на поверхности свободной части мантии одинакова и в принятых безразмерных
единицах равна нулю. На этих рисунках вся земная поверхность показана в развернутой
проекции.
На рис. 3 (7 кадров) приведены результаты расчета эволюции
системы мантия-континент.
Форма континента и его положение для определенности выбраны подобными современной Африке.
Но структура мантийной конвекции не может соответствовать современной Земле, так состояние
мантийной конвекции в момент помещения континента выбрано произвольно. Таким образом,
рассматриваемая модель служит лишь для выявления принципиальной возможности дрейфа континента
и его закономерностей. Цветом указано распределение вычисленного безразмерного теплового
потока (числа Нуссельта) вдоль поверхности Земли. Напомним, что температура на поверхности
континента и на поверхности свободной части мантии одинакова и в принятых безразмерных
единицах равна нулю. На этих рисунках вся земная поверхность показана в развернутой
проекции.
 Более подробно эволюция дрейфа континента в модели 1 представлена в виде анимационного
фильма anim01, включающего 55 кадров. Как видно из этих рисунков, при слабой конвекции в мантии возникает только
несколько восходящих и нисходящих конвективных потоков. При этом нисходящие потоки практически
оказываются связанными в единую систему. Континент сначала затягивается на место какого
либо нисходящего мантийного потока. Но поскольку форма и размеры континента не совпадают
области нисходящего потока на земной поверхности, то это положение континента оказывается
нестационарным. Так в рассмотренной модели с постоянной вязкостью не учитывается
океаническая литосфера и континент всего один, то его движение оказывается свободным.
Континент начинает дрейфовать вдоль системы связанных нисходящих мантийных потоков.
Так как континент тормозит выход тепла из мантии, то при неподвижным достаточно большим
континентом мантия начинает прогреваться и, примерно через 200-400 млн. лет возникает
восходящий горячий конвективный поток [Трубицын и Бобров, 1996]. При быстром движении
континента под ним не успевает возникнуть горячий восходящий мантийный поток. Но, как
видно из рисунков приложения А, при замедлении дрейфа сзади континента восходящий
поток может частично возникать.
Более подробно эволюция дрейфа континента в модели 1 представлена в виде анимационного
фильма anim01, включающего 55 кадров. Как видно из этих рисунков, при слабой конвекции в мантии возникает только
несколько восходящих и нисходящих конвективных потоков. При этом нисходящие потоки практически
оказываются связанными в единую систему. Континент сначала затягивается на место какого
либо нисходящего мантийного потока. Но поскольку форма и размеры континента не совпадают
области нисходящего потока на земной поверхности, то это положение континента оказывается
нестационарным. Так в рассмотренной модели с постоянной вязкостью не учитывается
океаническая литосфера и континент всего один, то его движение оказывается свободным.
Континент начинает дрейфовать вдоль системы связанных нисходящих мантийных потоков.
Так как континент тормозит выход тепла из мантии, то при неподвижным достаточно большим
континентом мантия начинает прогреваться и, примерно через 200-400 млн. лет возникает
восходящий горячий конвективный поток [Трубицын и Бобров, 1996]. При быстром движении
континента под ним не успевает возникнуть горячий восходящий мантийный поток. Но, как
видно из рисунков приложения А, при замедлении дрейфа сзади континента восходящий
поток может частично возникать.

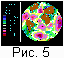 На рис. 4 - 6 приведены результаты расчета эволюции мантийной конвекции с
пятью плавающими континентами при числе Рэлея Ra =106. На рис. 4 приведено рассчитанное
распределение температуры (фиолетовая кривая) и теплового потока (красная кривая) вдоль
радиуса в мантии. На рис. 5 (4 кадра) представлены результаты расчета эволюции системы
мантия-континенты для модели 2. В отличие от модели 1 на этих рисунках показан вид земного
полушария со стороны точки наблюдения с широтой в 90o и долготой 0o. Начальное положение
и форма континентов взяты подобными континентам Африка, Северная и Южная Америка, Австралия
и Евразия. Форма каждого континента описана приближенно по 12 угловым точкам контура. Так
как структура конвекции в момент помещения континентов в мантию выбрано произвольным, то
рассчитанная модель не ставит целью проследить дрейф континентов на реальной Земле, а лишь
выявляет принципиальные особенности дрейфа континентов, в частности возможность их
объединения в суперконтиненты и последующего расхождения.
На рис. 4 - 6 приведены результаты расчета эволюции мантийной конвекции с
пятью плавающими континентами при числе Рэлея Ra =106. На рис. 4 приведено рассчитанное
распределение температуры (фиолетовая кривая) и теплового потока (красная кривая) вдоль
радиуса в мантии. На рис. 5 (4 кадра) представлены результаты расчета эволюции системы
мантия-континенты для модели 2. В отличие от модели 1 на этих рисунках показан вид земного
полушария со стороны точки наблюдения с широтой в 90o и долготой 0o. Начальное положение
и форма континентов взяты подобными континентам Африка, Северная и Южная Америка, Австралия
и Евразия. Форма каждого континента описана приближенно по 12 угловым точкам контура. Так
как структура конвекции в момент помещения континентов в мантию выбрано произвольным, то
рассчитанная модель не ставит целью проследить дрейф континентов на реальной Земле, а лишь
выявляет принципиальные особенности дрейфа континентов, в частности возможность их
объединения в суперконтиненты и последующего расхождения.
Как видно из рис. 5, три континента (Африка, Евразия и Северная Америка) начинают дрейфовать на север. Два других континента (Австралия и Южная Америка) движутся на юг.
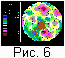 На рис. 6. (11 кадров) показана дальнейшая эволюция системы мантия-континенты. Поскольку
к этому моменту времени континенты уходят на другую половину земного шара, то на этих
рисунках показан вид земного шара со стороны точки с координатами 45o южной
широты и 210o
восточной долготы. Как видно из этих рисунков, в момент безразмерного времени t=14.0298
три континента (Южная Америка, Евразия и Австралия) объединяются в суперконтинент. В момент
t=14.03296 все пять континентов объединяются в единый суперконтинент Пангею. Так как под
Пангеей накапливается тепло, то мантийное вещество в этом месте становится легче. Нисходящий
конвективный поток сменяется на восходящий, который раскалывает Пангею к моменту безразмерного
времени t =14.0355. После распада Пангеи на ее месте еще долго остается система горячих
восходящих мантийных потоков, аналогичных гигантской горячей аномалии под Тихим океаном.
На рис. 6. (11 кадров) показана дальнейшая эволюция системы мантия-континенты. Поскольку
к этому моменту времени континенты уходят на другую половину земного шара, то на этих
рисунках показан вид земного шара со стороны точки с координатами 45o южной
широты и 210o
восточной долготы. Как видно из этих рисунков, в момент безразмерного времени t=14.0298
три континента (Южная Америка, Евразия и Австралия) объединяются в суперконтинент. В момент
t=14.03296 все пять континентов объединяются в единый суперконтинент Пангею. Так как под
Пангеей накапливается тепло, то мантийное вещество в этом месте становится легче. Нисходящий
конвективный поток сменяется на восходящий, который раскалывает Пангею к моменту безразмерного
времени t =14.0355. После распада Пангеи на ее месте еще долго остается система горячих
восходящих мантийных потоков, аналогичных гигантской горячей аномалии под Тихим океаном.
 Более подробно эволюция дрейфа пяти континентов в модели 2 представлена в виде анимационного
фильма anim02, включающего 101 кадр. Этот фильм содержит 15
кадров для начального этапа эволюции, рассматриваемого с одной стороны и 86 кадров для
этапа эволюции с объединением трех и пяти континентов.
Более подробно эволюция дрейфа пяти континентов в модели 2 представлена в виде анимационного
фильма anim02, включающего 101 кадр. Этот фильм содержит 15
кадров для начального этапа эволюции, рассматриваемого с одной стороны и 86 кадров для
этапа эволюции с объединением трех и пяти континентов.
На недавно состоявшейся Международной Гордоновской Конференции (Gordon Research Conference - Interior of the Earth, 28 June - 3 July, 1998, Бостон, США) в качестве важнейших нерешенных проблем наук о Земле указаны две проблемы: объяснение причины имеющих место в истории Земли неоднократных объединений и расхождений континентов и объяснение природы континентальной литосферы, ее образования и эволюции.
Решение этих проблем будет фактически следующим важном этапом в развитии концепции о строении и процессах в Земле. Тектоника литосферных плит объяснила природу только океанической литосферы, рассматривая континенты лишь как пассивно дрейфующие неоднородности, вмороженные в океанические плиты. Так как океанические литосферные плиты существуют не более 200 млн. лет, то тектоника плит в принципе не может объяснить глобальные геологические процессы длительностью в миллиарды лет, в частности причину образования и распада суперконтинентов. Очевидно, что без континентов не могла бы возникнуть и континентальная литосфера, возраст которой больше океанических плит. Свойства и эволюция континентальной литосферы должны определяться долгоживущими движущимися континентами.
Новый подход к глобальной тектонике был выдвинут в работах [Trubitsyn and Rykov, 1995; Трубицын и Рыков, 1997; 1998a, б, в]. На основе детальных численных экспериментов на двух и трехмерных моделях в декартовых координатах было показано, что континенты - не пассивные включения в литосферные плиты, а, наоборот, являются главными регуляторами всей глобальной тектоники Земли и саморегуляторами своего дрейфа. Именно континенты, возникшие более трех млрд. лет тому назад сформировали континентальную литосферу и обусловили ее свойства, отличные от океанической литосферы.
В настоящей работе впервые представлена трехмерная сферическая модель мантийной конвекции, взаимодействующей с несколькими плавающими континентами. Условие прилипания на погруженной в мантию части поверхности континентов вводит механическое взаимодействие мантии и континентов. Условие непрерывности температуры и теплового потока на этих границах вводит тепловое взаимодействие мантии и континентов. Континенты взаимодействуют между собой при непосредственном столкновении и опосредовано через мантию, изменяя ее структуру. Решение системы взаимосвязанных уравнений переноса массы, тепла и импульса для вязкой мантии и уравнений Эйлера для твердых континентов впервые позволило самосогласованно описать эволюцию системы мантия-континенты на трехмерной модели. Благодаря сферичности модели (в которой отсутствую боковые границы) удалось проследить очень длительную эволюцию дрейфа континентов и впервые описать как образование, так и распад суперконтинентов.
Следует отметить, что представленная модель доказывает только принципиальную возможность образования и распада суперконтинентов без непосредственной привязки к реальной Земле. Это обусловлено тем, что структура мантийной конвекции в момент помещения континентов была взята из модельных расчетов установления конвекции. В то время как структура мантийной конвекции возникла в результате длительной эволюции Земли под влиянием большого числа осложняющих процессов, например, дифференциации вещества, перераспределения источников тепла, существенного изменения вязкости и др.
Однако решение этой проблемы оказывается возможным при использовании данных сейсмической томографии. Пересчет распределения скоростей сейсмических волн дает современное мгновенное распределение температуры в Земле. Поэтому решение системы уравнений конвекции с плавающими континентами на основании развитого авторами математического аппарата даст возможность определить скорости мантийных течений, которые существенного зависят от прилипания к твердым континентам. Кроме этого, развитый авторами аппарат позволяет рассчитать и сами скорости континентов, распределение теплового потока, рельеф, гравитационное поле и распределение напряжений во всей Земле. После оптимизации параметров модели с условием согласования результатов расчета со всем комплексом имеющихся данных наблюдений будет построена полная геодинамическая модель Земли. Эта модель позволит на компьютере видеть процессы в недрах Земли, в частности в результате которых формируются месторождения полезных ископаемых и изменяется общее поле напряжений
Бобров А. М., Трубицын В. П., Времена перестроек мантийных течений под континентами, Физика Земли, (7), 5-13, 1995, (Bobrov A. M., Trubitsyn V. P., Times of rebuilding of mantle flows beneath continent, Izvestiya, Physiscs of the Solid Earth, 31, 551-559, 1996), (English translation of Fizika Zemli, (7), 5-13, 1995, Published by American Geophysical Union and Geological Society of America).
Ландау Л. Д., Лифшиц Е. М., Гидродинамика, c. 736, Наука, Москва, 1986.
Ландау Л. Д., Лифшиц Е. М., Механика, c. 203, Наука, Москва, 1965.
Рыков В. В., Трубицын В. П., Численное моделирование мантийной конвекции и тектоники континентальных плит, Вычислительная сейсмология, Геодинамика и прогноз землетрясений, 26, 94-102, 1994, (Rykov V. V. and Trubitsyn V. P., Numerical technique for calculation of three-dimensional mantle convection and tectonics of continental plates, in: Computational Seismology and Geodynamics, ed. by D. K. Chowdhury, Am. Geophys. Un., Vol. 3, pp. 17-22, Washington D.C., 1996a, English translation of Vychisliteljnaya seismologiya,(26), pp. 94-102, Nauka, Moscow. 1994).
Рыков В. В., Трубицын В. П., Трехмерная модель мантийной конвекции с движущимися континентами, Вычислительная сейсмология, Теоретические проблемы геодинамики и сейсмологии, 27, 21-41, 1994, (Rykov V. V., and Trubitsyn V. P., 3-D model of mantle convection incorporating moving continents, in: Computational Seismology and Geodynamics, ed. by D. K. Chowdhury. Am. Geophys. Un., Vol. 3, 23-32, Washington D.C., 1996b, English translation of Vychisliteljnaya seismologiya, (27), pp. 21-41, Nauka, Moscow, 1994).
Самарский А. А., Николаев Е. С., Методы решения сеточных уравнений, c. 591, Наука, Москва, 1978, (Samarskii A. A., and Nikolaev E. S., Method of solving finite-difference equations (in Russian), p. 591, Nauka, Moscow, 1978).
Теркотт Д., Шуберт Дж., Геодинамика, c. 730, Мир, Москва, 1985, (Turcotte D. L., and Schubert G., Geodynamics: in: Applications of Continuum Physics to Geological Problems, 449 pp., John Wiley, New York, 1982).
Трубицын В. П., Фрадков А. С., Конвекция под континентами и океанами, Физика Земли, (7), 3-14, 1985, (Trubitsyn V. P., and Fradkov A. S., Convection under continents and oceans, Izvestiya, Physics of the Solid Earth, 21, (7), 491-498, 1985, (English translation of Fizika Zemli, (7), 3-13, 1985, Published by American Geophysical Union and Geological Society of America).
Трубицын В. П., Фрадков А. С., Силы вязкого торможения океанической литосферы, Физика Земли, (6), 3-16, 1986.
Трубицын В. Р. Бобров А. М., Кубышкин В. В., Теплова конвекция в мантии, вызванная горизонтальным и вертикальным градиентом температуры, Физика Земли, (5), 12-23, 1991.
Трубицын В. Р. Бобров А. М., Кубышкин В. В., Влияние континентальной литосферы на структуру мантийной тепловой конвекции, Физика Земли, (5), 3-11, 1993, (Trubitsyn V. P., and Bobrov A. M. and Kubyshkin V. V., Influence of continental lithosphere on structure of mantle thermal convection, Izvestiya, Physiscs of the solid Earth, 29, 377-385, 1993, English translation of Fizika Zemli, (9), 27-37, 1993, Published by American Geophysical Union and Geological Society of America).
Трубицын В. П., Белавина Ю. Ф., Рыков В. В., Тепловое и механическое взаимодействие мантии с континентальной литосферой, Физика Земли, РАН, (11), 3-13, 1993, (Trubitsyn V. V., Belavina Yu. F., and Rykov V. V., Thermal and mechanical interaction of mantle and continental lithosphere, Izvestiya, Physics of the Solid Earth, 29, 933-945, 1993, English translation of Fizika Zemli, (11), 3-13, 1993, Published by American Geophysical Union and Geological Society of America).
Трубицын В. П., Бобров А. М., Эволюция структуры мантийной конвекции после распада суперконтинента, Физика Земли, (9), 27-37, 1993, (Trubitsyn V. P., and Bobrov A. M., Structure evolution of mantle convection after breakup of supercontinent, Izvestiya, Physiscs of the Solid Earth, 29, 768-778, 1994, English translation of Fizika Zemli, (9), 27-37, 1993, Published by American Geophysical Union and Geological Society of America).
Трубицын В. П., Белавина Ю. Ф., Рыков В. В., Тепловая конвекция в мантии с переменной вязкостью и континентальной плитой конечных размеров, Физика Земли, (7/8), 5-17, 1994, (Trubitsyn V. V., Belavina Yu. F., and Rykov V. V., Thermal mantle convection in a varying viscosity mantle with a finite-sized continental plate, Izvestiya, Physics of the Solid Earth, 30, 587-599, 1995, English translation of Fizika Zemli, (7/8), 5-17, 1994, Published by American Geophysical Union and Geological Society of America).
Трубицын В. П., Бобров А. М., Структура мантийной конвекции под неподвижными континентами, Вычислительная сейсмология, Современные проблемы сейсмичности и динамики Земли, (28), 22-31, Наука, Москва, 1996.
Trubitsyn V. P., and Bobrov A. M., Structure of mantle convection beneath stationary continents, in: Computational Seismology and Geodynamics, ed. by D. K. Chowdhury. Am. Geophys. Un., Vol. 4, pp. 42-53, Washington D.C, 1997, (English translation of Vychisliteljnaya seismologiya, (28), pp. 22-31, Nauka, Moscow, 1996).
Трубицын В. П., Бобров А. М., Тепловое и механическое взаимодействие континентов с мантией, Вычислительная сейсмология, Теоретические проблемы геодинамики сейсмологии, 27, 3-20, 1994, (Trubitsyn V. P., and Bobrov A. M., Thermal and mechanical interaction of continents with the mantle in: Computational Seismology and Geodynamics, ed. by D. K. Chowdhury. Am. Geophys. Un., Vol. 3, pp. 33-41, Washington D.C, 1996, English translation of Vychisliteljnaya seismologiya, (27), pp. 3-20, Nauka, Moscow, 1994).
Трубицын В. П., Рыков В. В., Механизм формирования наклонных зон субдукции, Физика Земли, (6), 1-12, 1997, (Trubitsyn V. P., and Rykov V. V., Mechanism of formation of an inclined subduction zone, Izvestiya, Physics of the Solid Earth, Official English translation of Fizika Zemli, (6), 1-12, 1997, Interperiodica Publishing, 33, (6), 427-437, Russia. 1997).
Трубицын В. П., Рыков В. В., Глобальная тектоника плавающих континентов и океанических литосферных плит, ДАН РАН, 359, (1), 109-111, 1998.
Трубицын В. П., Рыков В. В., Самосогласованная 2-D модель мантийной конвекции с плавающим континентом, Российский ж. наук о Земле, (электронная версия), Russian J. Earth's Sciences, (electronic), 1, (1), июль, 1998, http://eos.wdcb.rssi.ru/rjes/rje98001/rje98001.htm
Трубицын В. П., Рыков В. В., Мантийная конвекция и глобальная тектоника Земли, Вестник ОГГГГ РАН, (электронная версия) (1 (3)), 1998, http://www.scgis.ru/russian/cp1251/dgggms/1-98/main.html
Christensen U., A numerical model of coupled subcontinental and oceanic convection, Tectonophysics, 95, 1-23, 1983.
Christensen U. R., Convection with pressure- and temperature- dependent non-Newtonian rheology, Geophys. J. Astr. Soc., 77, 343-384, 1984.
Christensen U. R., Heat transfer by variable viscosity convection, II. Pressure influence, non-Newtonian rheology and decaying heat sources, Phys. Earth Planet. Inter., 37, 183-205, 1985.
Christensen U. R., and Yuen D. A., The interaction of a subducting lithospheric slab with a chemical or phase boundary, J. Geophys. Res., 89, 4389-4402, 1984.
Doin M.-P., Fleitout L., and Christensen U., Mantle convection and stability of depleted and undepleted continental lithosphere, J. Geophys. Res., 102, 2771-2787, 1997.
Fukao Y., Maruyama S., Obaya shi M., and Inoue H., Geological implication of the whole mantle P -wave tomography, Jour. Geol. Soc. Japan, 100, 4-23, 1994.
Glatzmaier G. A., Numerical simulation of mantle convection: Time-dependent, three-dimensional, compressible, spherical shell, Geophys. astrophys. Fluid Dyn, 43, 223-264, 1988.
Guillou, L., and Jaupart C., On the effect of continents on mantle convection, J. Geophys. Res., 100, 24,217-24,238, 1995.
Gurnis M., Large-scale mantle convection and aggregation and dispersal of supercontinents, Nature, 332, 696-699, 1988.
Gurnis M., and Zhong S., Generation of long wavelength heterogeneity in the mantle dynamics interaction between plates and convection, Geophys. Res. Lett., 18, 581-584, 1991.
Lenardic A., and Kaula W. M., Tectonic plates, D

 thermal structure,
and the nature of mantle plumes, J. Geophys. Res., 99, 15,697-15,708, 1994.
thermal structure,
and the nature of mantle plumes, J. Geophys. Res., 99, 15,697-15,708, 1994.
Lowman J. P., and Jarvis J. T., Mantle convection flow reversals due to continental collisions, Geophys. Res. Lett., 20, 2091-2094, 1993.
Lowman J. P., and Jarvis J. T., Continental collisions in wide aspect ratio and high Rayleigh number two-dimensional mantle convection models, J. Geophys. Res., 101, (B11), 25,485-25,497, 1996.
Lowman J. P., and Jarvis J. T., Mantle convection models of continental collision and breakup incorporating\refparbreakfinite thickness plates, Phys. Earth Planet. Inter., 88, 53068, 1995.
Jacoby W. R., and Schmeling H., On the effects of the lithosphere on mantle convection and evolution, Phes. Earth Planet. Int., 9, 305-319, 1982.
Lux R. A., Davies G. F., and Thomas J. H., Moving lithospheric plates and mantle convection, Geophys. J. R. Astron. Soc., 57, 209-228, 1979.
Machetel P., and Weber P., Intermittent layered convection in a model mantle with an endothermic phase change at 670 km, Nature, 350, 55-57, 1991.
Parmentier E. M., Sotin C., and Travis B. J., Turbulent 3-D thermal convection in an infinite Prandl number, volumetrically heated fluid; Implication for mantle dynamics, Geophys. J. Int., 116, 241-254, 1994.
Nakakuki T., Yuen D. A., and Honda S., The interaction of plumes with the transition zone under continents and oceans, Earth Planet. Sci. Lett., 146, 379-391, 1997.
Solheim L. P., and Peltier W. R., Phase boundary deflections at 660-km depth and episodically layered isochemical convection in the mantle, J. Geophys. Res., 99, 15,861-15,875, 1994.
Tackley P. J., Stevenson D. J., Glatzmaier G. A., and Schubert G., Effect of multiple phase transitions in three dimension spherical model of convection in Earth's mantle, J. Geophys. Res., 99, 15,877-15,901, 1994.
Trubitsyn V. P., and Rykov V. V., A 3-D numerical model of the Wilson cycle, J. Geodynamics, 20, 63-75, 1995.
Zalesak S. T., Fully multidimensional flux-correced transport algorithms for fluids, J. Comp. Phys., 31, 335-361, 1979.
Zhong S., and Gurnis M., 1993 Dynamic feedback between a continentlike raft and thermal convection, J. Geophys Res., 98, 12,219-12,232, 1993.
Zhong, Sh., and Gurnis M., Role of plates and temperature-dependent viscosity in phase change dynamics, J. Geophys. Res., 99, 15,903-15,917, 1994.
 |