
С. М. Молоденский
Объединенный Институт физики Земли РАН, Москва, Б. Грузинская ул., д. 10
Как известно, нутация Земли и планет в пространстве полностью определяется
эйлеровскими углами
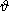 E, fE, yE,
описывающими положение Тиссерановых (связанных с телом планеты) осей
(x, y, z) относительно
неподвижной системы координат. В то же время, динамические уравнения движения
реальной модели планеты определяют только компоненты
(wx ,
wy ,
wz) угловой скорости
вектора
w относительно подвижной
системы
координат
(x, y, z). В случае аксиально симметричной планеты
(когда главные моменты инерции А, В, С удовлетворяют условию
A=B ), эйлеровские углы
связаны с этими компонентами известными кинематическими соотношениями
Пуансо [Ландау и Лифшиц, 1964]; в случае же
A
E, fE, yE,
описывающими положение Тиссерановых (связанных с телом планеты) осей
(x, y, z) относительно
неподвижной системы координат. В то же время, динамические уравнения движения
реальной модели планеты определяют только компоненты
(wx ,
wy ,
wz) угловой скорости
вектора
w относительно подвижной
системы
координат
(x, y, z). В случае аксиально симметричной планеты
(когда главные моменты инерции А, В, С удовлетворяют условию
A=B ), эйлеровские углы
связаны с этими компонентами известными кинематическими соотношениями
Пуансо [Ландау и Лифшиц, 1964]; в случае же
A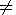 B общие соотношения
между
B общие соотношения
между
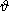 E, fE, yE
и
(wx, wy,
wz) представляют
довольно сложную
(нелинейную) систему обыкновенных дифференциальных уравнений, которая до
настоящего времени во многих существенных деталях не была исследована.
E, fE, yE
и
(wx, wy,
wz) представляют
довольно сложную
(нелинейную) систему обыкновенных дифференциальных уравнений, которая до
настоящего времени во многих существенных деталях не была исследована.
Как было показано в [Молоденский, 1980; Zharkov et al., 1996], в случае достаточно малых нарушений аксиальной симметрии (если параметр
удовлетворяет условию
|h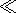 1| ),
уравнения Эйлера могут
быть решены методом возмущений
по степеням этого малого параметра; при таком подходе,
члены порядка
h включают только короткопериодические (полусуточные)
возмущения значений
1| ),
уравнения Эйлера могут
быть решены методом возмущений
по степеням этого малого параметра; при таком подходе,
члены порядка
h включают только короткопериодические (полусуточные)
возмущения значений
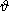 E ,
fE ,
yE . Тем не менее,
этот результат нельзя рассматривать, как окончательное решение
рассматриваемой задачи, поскольку поправки порядка
h2 могут содержать и длиннопериодные
члены,
возмущающие не только мгновенные значения амплитуд нутаций, но и их
средние значения. Как известно, современные радиоинтерферометрические
наблюдения наиболее чувствительны именно к этим возмущениям, поэтому
их анализ представляет наибольший интерес для практического применения.
E ,
fE ,
yE . Тем не менее,
этот результат нельзя рассматривать, как окончательное решение
рассматриваемой задачи, поскольку поправки порядка
h2 могут содержать и длиннопериодные
члены,
возмущающие не только мгновенные значения амплитуд нутаций, но и их
средние значения. Как известно, современные радиоинтерферометрические
наблюдения наиболее чувствительны именно к этим возмущениям, поэтому
их анализ представляет наибольший интерес для практического применения.
Ниже даны простые аналитические выражения, описывающие эти поправки с точностью порядка h4 .
Как известно, современные радиоинтерферометрические наблюдения определяют движение фиксированных точек R земной поверхности относительно неподвижной системы координат, которая связывается обычно с внегалактическими радиоисточниками. В то же время, известное уравнение Лиувилля
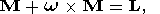 , , | (1) |
где точкой над символом обозначена производная по времени, w - угловая скорость вращения тиссерановой системы координат (x, y, z), M - угловой момент, L - момент внешних сил, определяет только движение вектора w относительно системы координат (x, y, z). Чтобы выразить компоненты вектора R через известные значения компонент (wx, wy, wz) удобно использовать соотношения Пуансо, которые связывают траекторию вектора w относительно подвижной системы координат (x, y, z) (полодию) c траекторией того же вектора в пространстве (герполодией).
В случае абсолютно твердой планеты с аксиально симметричным эллипсоидом инерции (когда A=B и все недиагональные компоненты тензора инерции Iik равны нулю), компоненты M и w связаны известным соотношением
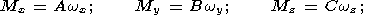 | (2) |
а момент L можно представить в форме
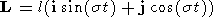 | (3) |
где i , j - единичные орты, ориентированные вдоль осей x и y , соответственно,
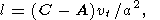 | (4) |
vt - амплитуда близсуточной компоненты приливного потенциала
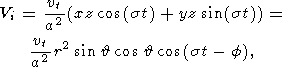 | (5) |
а - средний радиус планеты,
(r, 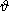 , f )
- сферические координаты,
s - приливная частота.
, f )
- сферические координаты,
s - приливная частота.
В самом общем случае, уравнение Лиувилля (1) представляет систему из трех нелинейных дифференциальных уравнений относительно трех неизвестных функций wx(t), wy(t), wz(t) . При h = 0 оно имеет очень простое точное решение. Действительно, подставив (2-4) в (1), мы получим
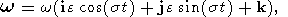 | (6) |
где k - единичный орт, совпадающий с осью z и
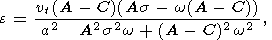 | (7) |
амплитуда нутации относительно подвижной системы координат (x, y, z).
Равенство амплитуд x - и y - компонент вектора в выражениях (6-7) является прямым следствием аксиальной симметрии рассматриваемой задачи. Вследствие этого, поверхности полодии и герполодии (определяемые как траектории движения вектора относительно подвижной и неподвижной систем координат, соответственно) являются коническими. В соответствии с известной теоремой Пуансо, отношение углов раскрытия этих конусов e и a определяется соотношением
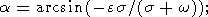 | (8) |
амплитуда нутационного движения неподвижного относительно системы координат (x, y, z) вектора R равна a + e для прямых компонент нутаций (когда направление вектора w совпадает с направлением нутационного движения) и a - e для обратных компонент (в противоположном случае).
В случае
h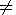 0
точные решения нелинейных динамических и кинематических
уравнений могут быть достаточно сложны. Поскольку для практических
приложений основной интерес представляют низкочастотные составляющие
возмущений, далее мы будем использовать метод их приближенного решения,
основанный на следующем:
0
точные решения нелинейных динамических и кинематических
уравнений могут быть достаточно сложны. Поскольку для практических
приложений основной интерес представляют низкочастотные составляющие
возмущений, далее мы будем использовать метод их приближенного решения,
основанный на следующем:
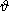 E, fE,
yE , можно выразить эти углы
и значения
w1(t) ,
w2(t) ,
w3(t) через известные компоненты
wx(t) ,
wy(t) ,
wz(t) . Поскольку кинематические
соотношения нелинейны, для их обращения используется метод возмущений
первого порядка по степеням малого параметра
h .
E, fE,
yE , можно выразить эти углы
и значения
w1(t) ,
w2(t) ,
w3(t) через известные компоненты
wx(t) ,
wy(t) ,
wz(t) . Поскольку кинематические
соотношения нелинейны, для их обращения используется метод возмущений
первого порядка по степеням малого параметра
h .
Используя выражение (5) для компонент приливного приливообразующего потенциала в декартовой системе координат, нетрудно найти момент сил, действующих на аксиально несимметричную планету
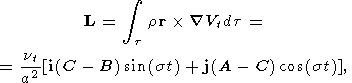 | (9) |
где t - объем, занимаемый Землей. Заменив в уравнениях (2) соотношение между wy и My формулой My = Bwy и подставив затем (2), (9) в уравнение Лиувилля (1), мы получим
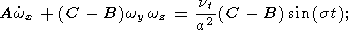 | (10a) |
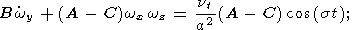 | (10b) |
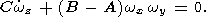 | (10c) |
Используя соотношения (6) , (7), легко видеть, что отношение входящих в соотношение (10с) членов Cwz и ( B-A)wxwy - порядка hevt /(ga) , где e – сжатие планеты , а g – ускорение свободного падения на ее поверхности. Это отношение во всех случаях пренебрежимо мало, поэтому приближение wz = w = const выполнено с большим запасом точности. В этом приближении решения уравнений (10а-10в) имеют вид
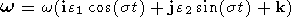 | (11a) |
где
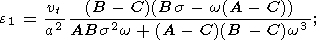 | (11b) |
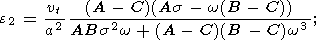 | (11c) |
Подставив выражения (11) в известные соотношения Эйлера для эйлеровских
углов ( 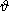 E, fE, yE )
с компонентами ( wx, wy,
wz ) [Ландау и Лившиц,
1964]:
E, fE, yE )
с компонентами ( wx, wy,
wz ) [Ландау и Лившиц,
1964]:
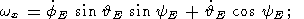 | (12a) |
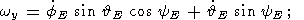 | (12b) |
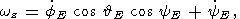 | (12c) |
мы получим систему из трех нелинейных обыкновенных дифференциальных
уравнений для трех неизвестных функций
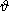 E, fE, yE.
E, fE, yE.
В случае аксиально симметричного тела (когда А=В ) и e1 = e2 = e , где e определено соотношением (7)) эти уравнения имеют элементарное решение (именуемое обычно соотношениями Пуансо) следующего вида:
 | (13a) |
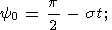 | (13b) |
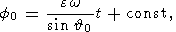 | (13c) |
которые показывают, что угловая частота и амплитуда нутационного движения в пространстве равны
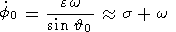 |
и
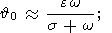 | (13d) |
(если эти амплитуды удовлетворяют условию
|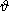 0|
0| 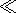 1 ).
1 ).
Чтобы оценить эффекты трехосности эллипсоида инерции в первом порядке
теории возмущений, выполним сначала
некоторые простейшие преобразования исходных уравнений. Домножив (12a),
(12b) на
cosyE и
sinyE и вычитая
затем результаты, нетрудно выразить значения
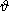 E через известные значения
e1, e2
:
E через известные значения
e1, e2
:
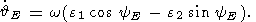 | (14a) |
Аналогично, умножив (12a) и (12b) на sinyE и cosyE и суммируя затем результаты: мы найдем:
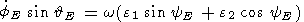 | (14b) |
Чтобы линеаризовать эти уравнения, представим их решения в виде суперпозиции
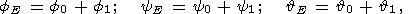 | (15) |
где
f0, y0,
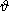 0 - решения нулевого приближения
(13а-с)
для аксиально симметричного тела, а
f1, y1,
0 - решения нулевого приближения
(13а-с)
для аксиально симметричного тела, а
f1, y1,
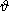 1 - малые
поправки, учитывающие эффекты трехосности эллипсоида инерции.
1 - малые
поправки, учитывающие эффекты трехосности эллипсоида инерции.
Подставив (15) и (11a) в (14a, b) и в (12c) и пренебрегая затем членами порядка h2 , получим
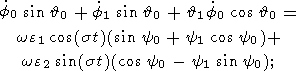 | (16a) |
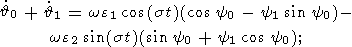 | (16b) |
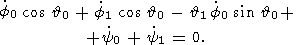 | (16c) |
Преобразуя главные члены в правых частях этих уравнений в соответствии с (13в)
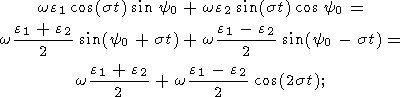 |
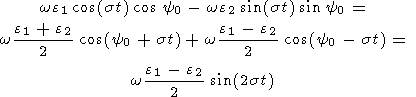 |
и учитывая, что в нулевом порядке теории возмущений значения
f0, 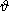 0,
y0 связаны с
e, w и
s соотношениями (13), мы получим после дифференцирования
этих соотношений по времени:
0,
y0 связаны с
e, w и
s соотношениями (13), мы получим после дифференцирования
этих соотношений по времени:
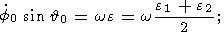 | (17a) |
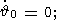 | (17b) |
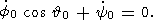 | (17c) |
С учетом (17) уравнения (16) можно записать в виде
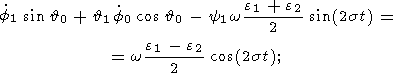 | (18a) |
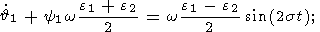 | (18b) |
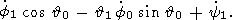 | (18c) |
Исключив из этих соотношений значения
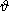 0 и
f0 с помощью (13a) и
(17c), мы получим окончательно
следующую систему из трех неоднородных линейных обыкновенных
дифференциальных уравнений:
0 и
f0 с помощью (13a) и
(17c), мы получим окончательно
следующую систему из трех неоднородных линейных обыкновенных
дифференциальных уравнений:
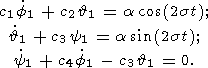 | (19) |
с коэффициентами
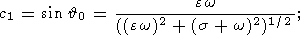 |
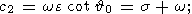 |
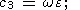 |
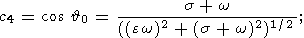 |
и с правой частью, пропорциональной
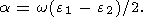 |
Поскольку система уравнений (19) третьего порядка, она имеет три линейно независимых однородных решения. Нетрудно показать, что эти решения не представляют существенного интереса для решения рассматриваемой здесь задачи, поскольку они описывают малые изменения углов Эйлера, связанные с произвольным бесконечно малым поворотом неподвижной системы координат в пространстве. Неоднородное же решение этих уравнений имеет вид
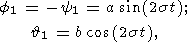 | (20) |
где
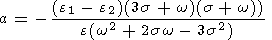 |
и
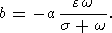 |
Эти выражения полностью определяют короткопериодические возмущения первого порядка, связанные с трехосностью эллипсоида инерции.
Чтобы найти короткопериодические возмущения в движении вектора
w в пространстве, введем
неподвижную
декартову систему координат ( e1, e2, e3 ) таким
образом,
чтобы ось
e3 совпадала с осью невозмущенного
конуса герполодии, а угол
fE был бы равен углу между линией
узлов и
вектором
e1 . Тогда соотношения между
компонентами ( w1, w2,
w3 ) и эйлеровскими углами
( 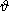 E, fE,
yE )
будут полностью аналогичны соотношениям
(12a-c) с той лишь разницей, что в них значения
fE следует заменить
на
yE , а значения
yE на
fE :
E, fE,
yE )
будут полностью аналогичны соотношениям
(12a-c) с той лишь разницей, что в них значения
fE следует заменить
на
yE , а значения
yE на
fE :
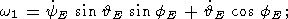 | (21a) |
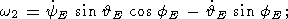 | (21b) |
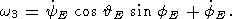 | (21c) |
В случае вынужденной нутации Земли амплитуда нутации в пространстве ew / (s + w) не превосходит нескольких секунд дуги, поэтому вместо (13а) можно использовать более простое выражение
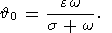 | (22) |
Подставив (15), (13b, c), (22) и (17) в (21), получим:
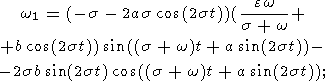 | (23a) |
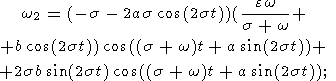 | (23b) |
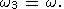 | (23c) |
Как и поправки первого порядка к эйлеровским углам (20), эти выражения также содержат только короткопериодные (полусуточные) возмущения.
Используем теперь известную теорему Пуансо, согласно которой качение полодии по герполодии происходит без проскальзывания. Вследствие этой теоремы, общий метод расчета долгопериодных возмущений герполодии может быть сформулирован следующим образом: пусть полная длина траектории движения вектора w относительно подвижной системы координат ( x, y, z ) определяется выражением
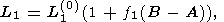 | (24a) |
где L1(0) - соответствующая длина в случае планеты с аксиально симметричным эллипсоидом инерции (при A=B ) и f1(B-A) - малая поправка, учитывающая эффекты трехосности.
Поскольку в случаях
A=B и
А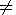 B рассматриваемые траектории совпадают с
окружностью (6), и с эллипсом
(11a), соответственно, фактически, функция
f1 будет описывать известную
разность длины эллипса (11a) с полуосями
we1,
we2
и длины
2pwe
окружности (6).
B рассматриваемые траектории совпадают с
окружностью (6), и с эллипсом
(11a), соответственно, фактически, функция
f1 будет описывать известную
разность длины эллипса (11a) с полуосями
we1,
we2
и длины
2pwe
окружности (6).
Аналогично, используя соотношения (23), нетрудно выразить полную длину траектории того же вектора w относительно неподвижной системы координат ( e1, e2, e3 ) виде
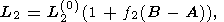 | (24b) |
где L2(0) = |s / (s + w)| L1(0) - полная длина для осесимметричного случая и f2(B-A) описывает разность длин траекторий для осенесимметричного и осесимметричного случаев.
Как отмечалось выше, отсутствие точных выражений для углов Эйлера через компоненты wx(t), wy(t) не позволяет определить эту функцию непосредственно. Однако, используя известные выражения (23), нетрудно найти ту часть этой функции f2(s)(B-A) , которая связана с короткопериодными (полусуточными) возмущениями герполодии. После этого оказывается возможным представить возмущение длины траектории вектора угловой скорости в пространстве в виде суммы известных короткопериодных возмущений L2(0)f2(s)(B-A) и неизвестных длиннопериодных возмущений L2(0)f2(1)(B-A) , определяющих изменение "среднего'' радиуса герполодии:
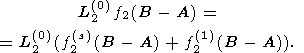 | (25a) |
В соответствии с теоремой Пуансо можно записать условие качения полодии по герполодии без проскальзывания в виде равенства длин траекторий, описываемых вектором угловой скорости за равные промежутки времени относительно подвижной и неподвижной систем координат:
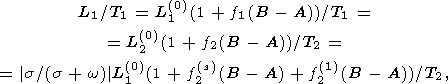 |
где T1 и T2 - полные периоды движения вектора w относительно подвижной и неподвижной систем координат соответственно. Поскольку
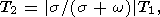 |
мы можем выразить неизвестное значение f2(1)(B-A) через известные функции f1(B-A) и f2(s)(B-A) в следующем простом виде:
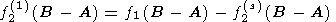 | (25b) |
Соответственно, изменение среднего радиуса герполодии (которое равно изменению амплитуды нутации dA , умноженному на w ) может быть представлено в форме
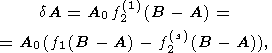 | (26) |
где A0 - невозмущенная амплитуда нутации в нулевом приближении, соответствующая аксиально симметричному случаю.
В соответствии с (11), полная длина траектории вектора w относительно подвижной системы координат ( x, y, z ) равна
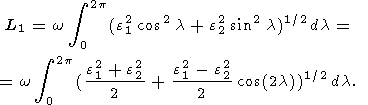 |
Разлагая подынтегральную функцию в ряд Тэйлора по малому параметру k = (e12 - e22)/(e12 + e22) с помощью (11b, c) и пренебрегая членами порядка k4 , получим
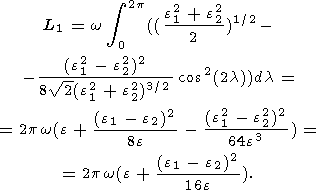 | (27a) |
Сравнивая это выражение с формулой (24а), мы получим
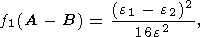 | (27b) |
где e1, e2 и e определяются выражениями (11b), (11c) и (7), соответственно.
Перейдем теперь к определению длины траектории движения вектора w относительно неподвижной системы координат ( e1, e2, e3 (герполодии).
Строго говоря, эта траектория не обязательно является замкнутой, поэтому постановка данной задачи требует некоторого уточнения. Очевидно, при наличии короткопериодных (полусуточных) возмущений в полодии и в герполодии последняя может быть замкнутой только при условии соразмеримости периодов нутационного движения относительно подвижных и неподвижных осей. Поскольку эти периоды равны, соответственно, p/s и 2p/|s + w|, в общем случае произвольных значений s и w герполодия замкнутой кривой не является.
Чтобы использовать теорему Пуансо в случае незамкнутых траекторий вектора угловой скорости в пространстве, определим "среднюю" длину этих траекторий соотношением
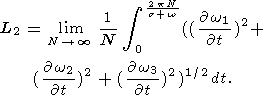 | (28) |
Подставив (23) в (28) и разлагая, как ранее, подынтегральную функцию в ряд Тэйлора с точностью до членов порядка k4 , будем иметь
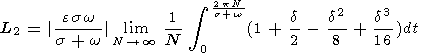 | (29a) |
где
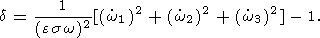 | (29b) |
Подставив (20a-c) в (26a, b), получим
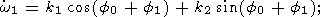 | (30a) |
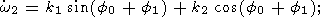 | (30b) |
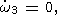 | (30c) |
где
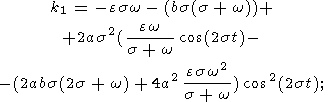 | (31a) |
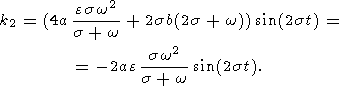 | (31b) |
Подставив эти выражения в (29) , (30a, b) и пренебрегая затем членами четвертого и высших порядков, мы найдем
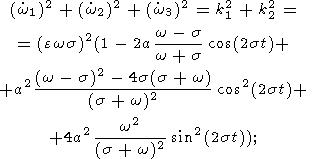 | (32a) |
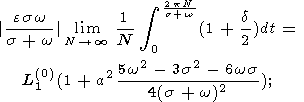 | (32b) |
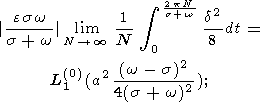 | (32c) |
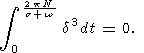 | (33) |
Суммируя эти выражения, получим окончательно
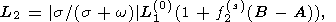 | (34a) |
где
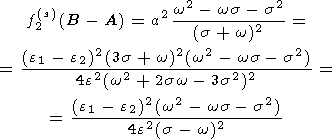 | (34b) |
Подстановка (34b) и (26b) в (23), дает следующее окончательное выражение для поправки к средней амплитуде нутации:
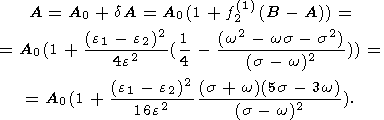 | (35) |
Следует отметить, что эта поправка обращается в нуль, если s = -w или если s = 3w/5 . Первый корень соответствует частоте прецессии. Обращение в нуль этого выражения для частоты прецессии свидетельствует о том, что постоянная прецессии зависит лишь от величины С - (A+B)/2 и практически не зависит от разности главных экваториальных моментов B-A .
Второй корень s = 3w/5 и корень знаменателя s = -w соответствуют случаям, когда частота вынужденной нутации в пространстве не мала по сравнению с ее частотой в подвижной системе (эти частоты соответствуют периодам нутационного движения в пространстве Ts = 5T0/8 и Ts = T0/2 соответственно, где T0 = 2p/w - звездные сутки). Движение с периодом Ts = T0/2 происходит в случае синхронного суточного и орбитального вращений (Когда в точках весеннего и осеннего равноденствий оси главных экваториальных моментов сохраняют неизменное направление). Очевидно, в этом случае амплитуды нутаций определяются не средним за период значением (А+В)/2 , а некоторыми "эффективными'' значениями параметров А, В (определяемых ориентацией главных экваториальных осей планеты в окрестностях тех точек траектории, где момент приливных сил имеет максимальную величину). В этом особом случае поправки к средним амплитудам нутаций пропорциональны не (e1 e2)2/e2 , а (e1 e2)/e . Это соображение объясняет, почему в предельном случае поправки второго порядка (35) стремятся к бесконечности.
Ландау Л. Д. и Е. М. Лифшиц Механика, М., Наука, 1964.
Молоденский С. М. Приливы, нутация и внутреннее строение Земли, Москва, "Наука'', 1980, 214 с.
Zharkov V. N., S. M. Molodensky, E. Groten, A. Brzezinski, and P. Varga. The Earth and its rotation. Low-frequency geodynamics, Heidelberg, Wichman Verlag, 1996, 531 pp.
 |