Заключение

Выше мы представили обзор и анализ термодинамических свойств геоматериалов, необходимых для изучения термодинамики глубинных оболочек Земли. Суммируем наиболее важные результаты анализа.

(1) В разделах 2-5 показано, что для самосогласованного определения всех параметров 2-го порядка необходимо знать три таких параметра. В связи с уравнениями состояния все термодинамические параметры разделяются на термические и калорические. Дана сводка подходов к определению уравнений состояния на основе экспериментальных данных. Эти подходы можно также сформулировать в виде соответствующих уравнений в частных производных. Из 16 параметров 3-го порядка независимыми являются четыре соответственно выбранных параметра. Обращается внимание на создание самосогласованной базы данных по термодинамическим параметрам минералов и приводится пример такой базы для трех минералов, основанной на входных (экспериментальных) значениях параметров a, K_S, C_P, ( K_S/ P)_T, (a/ T)_P, ( C_P/ T)_P и ( K_S/ T)_P.

(2) Каждый из восьми параметров 2-го порядка проанализирован отдельно по следующему плану: вывод тождественных соотношений между их P-T производными, оценки собственных и внешних ангармонических вкладов в температурных производных, полезные упрощения этих соотношений и их следствия, явные приближенные зависимости параметров 2-го порядка от давления и температуры.

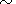(3) В анализе коэффициента теплового расширения (раздел 6) обобщается формула Берча для a = a(P) при T (или S ) = const. Показано, что a в нижней мантии по обобщенной формуле очень чувствительно к допускаемым значениям смешанной P-T производной модуля сжатия K_T в области d K₀/dT (0-4) 10^-4 K^-1. Выбор значения около 2 10^-4 K^-1 приводит к a нижней мантии, близкому к величинам по (экспоненциальным) законам О. Андерсена и др. [1993] и Шоплы и Белера [1992]. На основе этих оценок и представленного обзора мы заключаем, что коэффициент теплового расширения убывает вдоль горячей адиабаты нижней мантии в 4-5 раз (от P = 0 до P = 1.35 Мбар). Анализируя степенной закон для a О. Андерсона, мы сформулировали строгие условия совместимости различных допущений об уравнении состояния и параметрах d_T, K_T, K и C_V и рассмотрели следствия этих допущений. Во многих случаях эти условия оказываются полезными для самосогласованного термодинамического анализа. Например, закон Берча в степенном виде K_T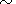 V^b приводит к K = const, K_T = K_T(V), d_T = K = const, уравнению Мурнагана (41) и, при C_V = const, a = a (V). Рассмотрение различных экстраполяций a в область высоких температур (при P=0 ) указывает на большую неопределенность a (до 30-50% при T 1500-2000 K ), что говорит о необходимости высокотемпературных измерений a для улучшения теоретических оценок.

(4) Изобарическая теплоемкость C_P в условиях нижней мантии (раздел 7) убывает приблизительно на 10% (вдоль горячей адиабаты от P=0 до P = 1.35 Мбар). При низких температурах T < Q собственный ангармонизм в ( C_P/ T)_P полностью доминирует, но при T > Q, когда ( C_P/ T)_P малo, его вклад составляет 15-30%.

(5) Подчеркивается различие между моделью теплового давления О. Андерсена и уравнением Ми-Грюнайзена (раздел 8). Эта модель имеет две важные особенности: тепловое давление обычно линейно по температуре, но его зависимость от объема определяется спецификой материала. По нашим оценкам, при T > Q нелинейные члены в P_th дают вклад не более 1-3%. В целом, мы указываем на существование, по крайней мере, четырех моделей термического уравнения состояния: уравнение Ми-Грюнайзена (или более общее решеточное ангармоническое уравнение состояния), модель с различными формами опорной изотермы P (V, T₀) и заданной зависимостью a (P, T), упомянутая выше модель О. Андерсена и уравнение вида (28) с допускаемыми зависимостями параметров от температуры.

(6) В разделе 9 рассмотрены подробнее параметры Андерсена-Грюнайзена d_T и d_S. Из обобщенной формулы Берча для a выведено явное выражение для d_T (V) при T (или S ) = const. Мы находим, что при d K₀/dT = 2.3 10^-4 K (см. вывод (3)) d_T в подошве мантии почти вдвое меньше величины при P = 0.

(7) Формулы для изотерм-адиабатических преобразований модулей сжатия выведены в разделе 10. Дополнительно (см. вывод (3)) проанализирована смешанная производная d K₀/dT, для которой получена новая формула (98). В целом, этот параметр для различных геоматериалов оценивается величинами порядка (1-3) 10^-4 K^-1.

Из анализа зависимости модулей сжатия от температуры мы заключаем, что ответственные за собственный ангармонизм параметры d^T_V = K - d_T и d^S_V при комнатной температуре в основном попадают в область между -4 и -1 и между - 1 и 1, соответственно. Однако их высокотемпературные значения находятся в области между -1 и 1 для d^T_V и между 0 и 1.5 для d^S_V. Приближение d^T_V 0 ( d_T K и K_T = K_T (V) ) оправдывается для многих, но не для всех минералов.

В связи с интерпретацией данных сейсмической томографии для нижней мантии, мы находим следующую область приемлемых значений для этого слоя Земли: d^T_V 0.2, q 0.8, g 1.1, d_T 3-3.3 и d_S 1.9-2.2.

Величины K_S при высокой температуре, вычисленные по степенному закону с d_S = const к линейной зависимости K_S от энтальпии (метод О. Андерсона), имеют ошибки порядка 2-6% и 1-3%, соответственно. Таким образом, подтверждается вывод О. Андерсена [1995] об эффективности оценок K_S по энтальпии.

(8) Ряд тождеств для параметра Грюнайзена g и производной q = ( lng/ ln V)_T приведен в разделе 11. Из них следует, что условия C_V = const или C_V = C_V (T) приводят к g = g (V) или g = f(V)/C_V(T), соответственно. Оба случая совместимы с моделью теплового давления О. Андерсона при t = aK_T = const или t = t (V). Любое из указанных условий для C_V также дает q = q(V) или q = const ; более того, из условия 0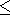 q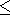 1 следует 0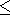 K - d_T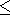 1 и наоборот. Величины q по термодинамическим оценкам попадают в основном в интервал 0.5-2. Этот параметр обычно убывает с давлением и температурой. В производной (g/ T)_P собственный ангармонизм в целом преобладает, указывая на существенную температурную зависимость в g (V,T). В дополнение ко многим известным выражениям для g (V) мы вывели новое соотношение, основанное на параметре l 1 - ( lngT/ ln V)_S 1. Случай g = 0 дает формулу Райса [Rice, 1965]. Изменение l в области 0-1 (соответственно, d^S_V l (1 + agT)^-1 изменяется примерно в том же интервале при agT 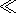1 ) заметно влияет на g при большом сжатии.

(9) Систематизированы тождества и приближенные соотношения для адиабатического градиента температуры t_S ( T/ P)_S. Термодинамические оценки параметра Белера n = ( lnt_S/ ln V)_T близки к результатам измерений для оливина, кварца и периклаза. Неопределенность оценок n порядка 1 вызваны ошибками в используемых термодинамических величинах. В производной (t_S/ T)_P преобладает собственный ангармонизм. При определении уравнения состояния по данным для t_S важную роль играет связь этого параметра с теплоемкостью.

Наконец, в разделах 6-8 и 10 мы испытали применимость уравнения Ми-Грюнайзена к описанию температурной зависимости параметров a, C_P, t и K_S. Эта модель качественно правильно описывает указанные зависимости, но не обеспечивает достаточно точного количественного согласия по всем параметрам. Поэтому (с учетом вывода (8)) следует с некоторой осторожностью подходить к применению этого уравнения в геофизике.

Благодарности

This document was generated by TeXWeb (Win32, v.1.0) on August 10, 1998.