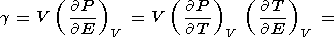
Параметр Грюнайзена определяется соотношением (8) или (14), которые далее приводят к тождествам
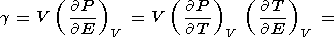 |
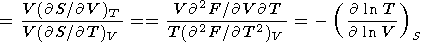 | (105) |
Типичные значения g по (8) или (14) заключены в пределах от 1 до 2 (таблица 2 и [Паньков и др., 1997]). Из 54 минералов, рассмотренных в статье [D. Anderson, 1989], лишь пять имеют g более 2, и ни один не имеет g более 3. Низкие g встречаются редко, например, g = 0.4 для a -кварца, 0.3 для коэсита и g< 0 для U 2 O, AgJ и b -кварца.
Производные g по V (или Р ) описываются параметром q, для которого из (8) и (100) имеем
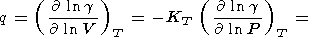 | (106) |
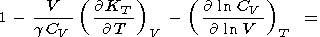 |
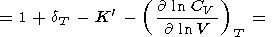 | (107) |
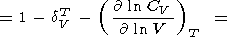 |
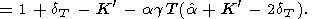 | (108) |
Ранее мы уже отмечали (см. (57) или (69) и (8)), что
СV = const привед
Если просто допустить чисто объемную зависимость
g, то из
(14), (33) и (106) мы найдем
Если сюда подставить
(KS/
Однако в общем случае
g = g (V,T)
мы находим из формулы для
g в (18)
что после исключения
L с помощью (85) приводит к тождеству
[Bassett et al., 1968]
которое сводится к (111) при
g = g (V).
В разделе 6 мы уже ссылались на сведения о параметре
q.
Данные по
q имеют следующие источники: 1) термодинамические
оценки по (108) или (111), 2) подгонка уравнений состояния типа
Ми-Грюнайзена к данным по
a(Т),
СР(Т) и
КS(Т) при
Р=0, 3)
ударноволновые данные [напр., McQueen, 1991;
Duffy and Ahrens, 1992a], 4) адиабатические измерения
температурного
градиента по
P [Boehler, 1982, 1983],
5) спектроскопия твердых тел
[например, Reynard et al., 1992; Williams et al.,
1987],
6) теоретические модели уравнений состояния
[напр., Isaak et al., 1990], 7) анализ
геофизических данных [O. Anderson, 1979b; D. Anderson,
1989].
Значения
q по (108), приведенные в таблице 3 и [Паньков и др., 1997],
попадают в интервал 0.5-2, исключая высокие значения для коэсита
(17), фаялита (2-3) и Fe-перовскита (4-5); слегка отрицатеьные
значения найдены для энстатита и FeO. С ростом
T при
P = const или ростом
P при
T (или
S ) = const величина
q уменьшается (см.
также раздел 6).
Для производной
g по температуре снова имеем разложение
типа (29)
где член собственного ангармонизма можно раскрыть с помощью
(18) и (85)
Как правило, этот член отрицателен и полностью доминирует в (114)
при
T < Q, но при высокой температуре его величина
сравнима с
q.
Таким образом, часто используемое допущение
g = g (V)
в общем случае
неудовлетворительно, а температурный эффект, оцениваемый по
(114), может служить некоторой мерой справедливости уравнения
Ми-Грюнайзена.
Другое полезное представление
(
Если
g = g (V), то
CV = CV
(S) или
CV = сonst.
Условие
CV (S) приводит к
Более того, (117) ведет к
CV(V,T) = CV
(Q/T) и
Q/T = f (S),
так что
g представляется в виде
g = - d lnQ/d
ln V,
где
Q - некоторая характеристическая температура.
Часто используемые зависимости решеточного
параметра
Грюнайзена от объема приводилось в разделе
6. Представляет
интерес также формула Райса [Rice, 1965]
вытекающая из (110) при условии
Условие
(
Уравнение (118) можно также рассматривать как частный
случай более общего представления
g = g (V,S).
Введем параметр
l
где
F = KS/r. Предполагая
l = l (S)
или
l = const, из (119) и (105) находим
где
g0 = g0
(S) и
V0 = V0 (S). Эта зависимость
g (x) с различными значениями
l иллюстрируется на рис. 10.
Мы видим, что
g (x) весьма чувствительно к изменениям
l в интервале от 0 до 1.
В геофизике условия, близкие к адиабатическим, возможны в
конвектирующей мантии и ядре, а также при распространении
сейсмических волн. Кроме того, состояния на ударной адиабате на
начальном участке ударного сжатия близки к адиабатическим.
Адиабаты данного материа образуют однопараметрическое
семейство кривых. Температура и давление при этом связаны
адиабатическим градиентом
tS, который,
учитывая определение
(10) и соотношения раздела 2, можно записать в виде
Типичные значения
tS, найденные
из этих тождеств, приведены в
таблице 2 и [Паньков и др., 1997].
Прямые измерения
tS при высоких
давлениях и температурах
были осуществлены в ряде работ [Джавадов, 1986;
Boehler and Ramakrishnan, 1980; Boehler, 1982, 1983].
Шопла и Белер [Choplas and Boehler, 1992]
сообщили о поправках к первоначальным
результатам Boehler [1982] для
tS.
Рассмотрим основные тождества и приближенные
соотношения для производных. Обозначая через
n логарифмическую производную
tS по объему и используя
q из (106), находим
(cравни с (45)).
Формулу (122) можно представить в разных формах, используя для
q выражения (113), (115) и (58). Ясно, что
n убывает при
изотермическом или адиабатическом сжатии. Простейшую
оценку
n можно получить, полагая
Типичные значения
q = 1-2 и
K
Переходя от переменных ( V,S ) к ( V,T ), представим
адиабатическую производную по объему в виде
Приближение (89) и
n
Записывая производную
tS по
Т в виде (29), имеем
или после подстановки
(
Величины
((
Заметим, что параметр
tS появляется
в любом выражении,
связанном с заменой переменных
P, S на
P, T, например,
- cоотношение, использованное при выводе (98).
При умеренных сжатиях объемная зависимость
tS может быть
описана степенным законом
где
n = n (T) или const,
tS0 = tS0
(T) и
V0 = V0 (T).
Эта формула
использовалась для описания измеренных
tS до
P = 50 кбар и
T = 1000 K [Boehler and Ramakrishnan, 1980;
Boehler, 1981, 1982].
Однако Шопла и Белер [Chopelas and Boehler, 1992], учитывая
изменение
dT с
V (cм. (46), (47)), нашли, что линейная зависимость
lntS от
V (n = mx) лучше описывает данные по
tS,
чем степенная зависимость, и следовательно,
где постоянная
m определялась по формуле
(cм.(122), где
СР приближенно заменено на
СV ). Таким образом, при
условии что
(
Измеренные значения
tS ( Р,Т ) позволяют прежде всего найти
изобарическую теплоемкость [Джавадов,
1986]
Это соотношение следует из тождества
Наоборот, если задается термическое уравнение
состояния и
tS (T)
при
Р=0, то (14) дает
CP (T) при
Р=0, и, следовательно, можно
определить калорическое уравнение состояния.
 = dT (V) и
t = aKT
= const ).
Таким образом, случай
СV = const или
СV = СV (T)
дают
эквивалентность двух неравенств
= dT (V) и
t = aKT
= const ).
Таким образом, случай
СV = const или
СV = СV (T)
дают
эквивалентность двух неравенств
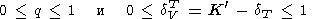
(109) 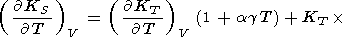
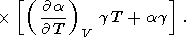
(110)  T)V из тождества (99), то
T)V из тождества (99), то
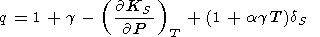
(111) 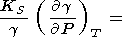
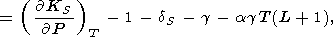
(112) 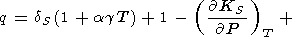
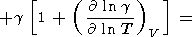
(113) 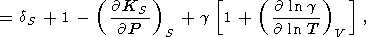
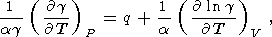
(114) 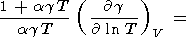
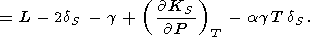
(115)  g/
g/ T)V следует из (8) и (69)
[Stacey, 1977b]
T)V следует из (8) и (69)
[Stacey, 1977b]
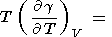
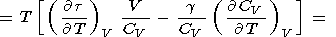
(116) 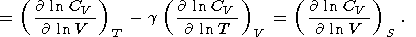
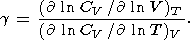
(117) 11.2. Некоторые явные зависимости
g от объема
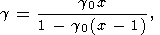
(118) 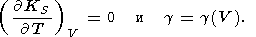
 KS/
KS/ T)V > 0
(см. раздел 10
и [D.Anderson, 1989]), выполняется для широкого
класса веществ и, как следствие, дает для
них нижнюю границу
зависимости
g (V), т.е.
q
T)V > 0
(см. раздел 10
и [D.Anderson, 1989]), выполняется для широкого
класса веществ и, как следствие, дает для
них нижнюю границу
зависимости
g (V), т.е.
q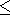 1 + g
,
g
1 + g
,
g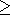 g
(x) по (118). Ранее эта граница
была указана на основе уравнения состояния Ми-Грюнайзена
[Калинин, Паньков, 1972], но она вытекает также из данного
термодинамического анализа.
g
(x) по (118). Ранее эта граница
была указана на основе уравнения состояния Ми-Грюнайзена
[Калинин, Паньков, 1972], но она вытекает также из данного
термодинамического анализа.
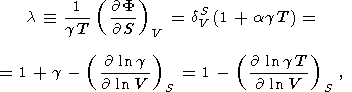
(119) 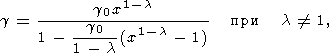
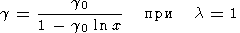
(120) 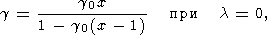
12. Адиабатический градиент температуры
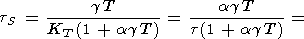
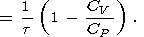
(121) 12.1. P-V-T производные tS
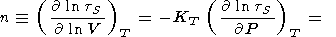
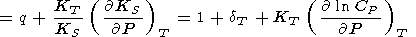
(122) 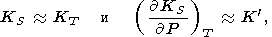
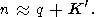
(123)  = 4-5 дают
n
= 4-5 дают
n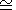 5-7. Наоборот,
данные по
n и
K
5-7. Наоборот,
данные по
n и
K позволяют
оценить
q. Если в (122) пренебречь
последним членом при
Т > Q [Boehler and Chopеlаs, 1992],
то
n
позволяют
оценить
q. Если в (122) пренебречь
последним членом при
Т > Q [Boehler and Chopеlаs, 1992],
то
n 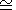 1+ dT.
1+ dT.
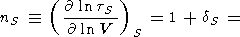
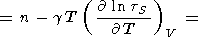
(124) 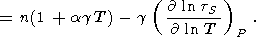
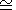 1 + dT
дают
nS
1 + dT
дают
nS 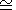 n
- g.
n
- g. 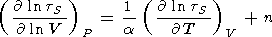
(125)  lntS/
lntS/ T)V из
(124)
T)V из
(124)
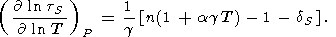
(126)  lntS)(
lntS)( ln V))P
и
n (связанное с внешним ангармонизмом),
вычисленные с помощью (126) и (122), приведены в таблице 2 и
[Паньков и др., 1997]. Они показывают, что в (125) преобладает
член, связанный с собственным ангармонизмом.
ln V))P
и
n (связанное с внешним ангармонизмом),
вычисленные с помощью (126) и (122), приведены в таблице 2 и
[Паньков и др., 1997]. Они показывают, что в (125) преобладает
член, связанный с собственным ангармонизмом.
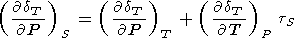
(127) 12.2. Явные зависимости tS от объема
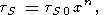
(128) 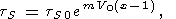
(129) 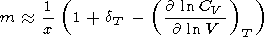
(130)  ln CV/
ln CV/ ln V)T
не зависит от
V,
производная
(
ln V)T
не зависит от
V,
производная
( dT/
dT/ x)T может
быть определена
по величине
m. Исаак [Isaak, 1993] применил
этот метод при анализе смешанной производной
x)T может
быть определена
по величине
m. Исаак [Isaak, 1993] применил
этот метод при анализе смешанной производной
 2 KS/
2 KS/ P
P T с помощью (91).
T с помощью (91).
12.3. Уравнение состояния, основанное на данных для tS, Р, Т.
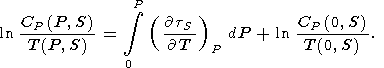
(131)  2T/
2T/ P
P S =
S =  2 T/
2 T/ S
S P.
Интеграл в (131) берется по адиабате и теплоемкость
СP(Т) при
Р=0 предполагается известной. Далее, зная какую-либо опорную
изотерму
V (P,T0), из (14) найдем термическое
уравнение состояния
P.
Интеграл в (131) берется по адиабате и теплоемкость
СP(Т) при
Р=0 предполагается известной. Далее, зная какую-либо опорную
изотерму
V (P,T0), из (14) найдем термическое
уравнение состояния
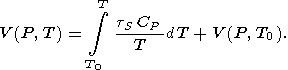
(132)
This document was generated by TeXWeb
(Win32, v.1.0) on August 10, 1998.