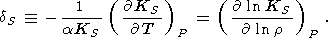
Здесь мы подробнее рассмотрим два полезных параметра Андерсона-Грюнайзена [Gruneisen, 1926; O. Anderson, 1966, 1967]: изотермический dT, введенный выше (cм. (31)), и адиабатический dS, определяемый ниже
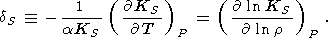 | (82) |
Оба параметра используются как в геофизических, так и физических работах [Chung, 1973; Barron, 1979]. Параметр dT применяется главным образм для анализа P-T зависимостей a, KT и t, а dS используется для оценки температурной зависимости KS и при рассмотрении связей скоростей упругих волн с термодинамическими данными [D. Anderson, 1987; O. Anderson et al., 1987; Isaak et al., 1992; Duffy and Ahrens, 1992].
С уменьшением температуры в области T 300 К при P = const оба параметра dT и dS возрастают из-за уменьшения a, но при высокой температуре T > Q они становятся более или менее постоянными [O. Anderson et al., 1992a]. Из (16) выводится точная связь между dT и dS [Birch, 1952]
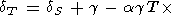 |
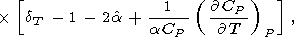 | (83) |
которую мы использовали для расчетов величин в таблице 3 [Паньков и др., 1997]. При выводе (83) мы попутно находим
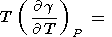 |
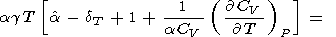 |
 | (84) |
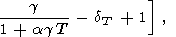 |
где для удобства введено обозначение
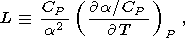 | (85) |
Величины
L и
( g /
g / T)P при
P = const = 0, вычисленные из (84) и (85),
также приведены в таблице 3 и [Паньков и др., 1997].
T)P при
P = const = 0, вычисленные из (84) и (85),
также приведены в таблице 3 и [Паньков и др., 1997].
Данные для ряда минералов [O. Anderson et al., 1992a]
показывают, что
( g/
g/ T)P=0
T)P=0 0 в достаточно широкой области
температур. Допуская
(
0 в достаточно широкой области
температур. Допуская
( g/
g/ T)P = 0 при
CV = const (T > Q), из (84)
получим
T)P = 0 при
CV = const (T > Q), из (84)
получим
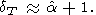 | (86) |
Так как при этом CV = const, мы получаем q = 0 и, согласно (35) и (42),
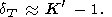 | (87) |
Однако оценка
dT по (42) с
q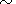 1 более точна, чем по (87). В этой
связи следует ожидать, что в (84)
1 более точна, чем по (87). В этой
связи следует ожидать, что в (84)
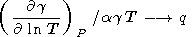 |
при CV const.
Используя (83), тождество (84) можно переписать как
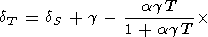 |
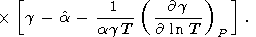 | (88) |
Если последний член мал, то имеем [O. Anderson et al., 1992a]
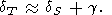 | (89) |
Это равенство рекомендуется для оценок при высокой температуре, если данных для использования тождеств (83) или (88) недостаточно.
Дополнительно к анализу параметра
dT (P,T), описанному в
разделах 6 и 8 рассмотрим следующие особенности поведения
dT.
1) Если
g = g (V), то
q = q (V), но, вообще говоря,
dT = dT
(V,T), так как
CV = CV
(V,T) и
K = K
= K (V,T). 2) Если
CV = CV
(T), то (42) выполняется и,
кроме того,
g = f(V)/CV(T),
q = q(V), хотя, вообще говоря,
K
(V,T). 2) Если
CV = CV
(T), то (42) выполняется и,
кроме того,
g = f(V)/CV(T),
q = q(V), хотя, вообще говоря,
K = K
= K (V,T) и
dT = dT
(V,T).
Комбинируя первое из этих допущений с условием
KT = KT
(V) (т.е.
dT = K
(V,T) и
dT = dT
(V,T).
Комбинируя первое из этих допущений с условием
KT = KT
(V) (т.е.
dT = K ), мы получаем
), мы получаем
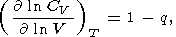 | (90) |
и поэтому CV принимает вид CV (V,T) = A (V)/B (T).
В разделе 2 мы привели аргументы в пользу убывания
dT с
давлением. Подобное же поведение этого параметра следует из
приближенной формулы (42), если учесть, что обе величины
K и
q также убывают с давлением. Точные соотношения для производных
dT по
P и
T следуют из определения
dT по (31)
и
q также убывают с давлением. Точные соотношения для производных
dT по
P и
T следуют из определения
dT по (31)
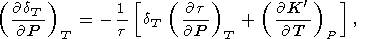 | (91) |
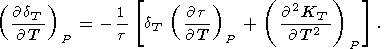 | (92) |
Если в (91) преобладает первый член, то получается необычный
случай
(( dT)/(
dT)/( P))T >
0.
В (92) имеем
(
P))T >
0.
В (92) имеем
( dT/
dT/ T)P < 0,
если пренебречь второй производной
KT по
T (по крайней мере при комнатной температуре).
Однако приближение
dT = K
T)P < 0,
если пренебречь второй производной
KT по
T (по крайней мере при комнатной температуре).
Однако приближение
dT = K (ближе к действительности
при
T > Q ) дает,
наоборот,
(
(ближе к действительности
при
T > Q ) дает,
наоборот,
( dT/
dT/ T)P > 0
вследствие
(
T)P > 0
вследствие
( K
K /
/ T)P
>0.
Экспериментальные данные указывают на слегка отрицательную
производную
((
T)P
>0.
Экспериментальные данные указывают на слегка отрицательную
производную
(( 2 KT)/(
2 KT)/( T2))P
при
T > Q [O. Anderson et al., 1992a].
T2))P
при
T > Q [O. Anderson et al., 1992a].
Наконец, уравнение состояния типа (28), из которого мы
находили коэффициент теплового расширения по (36), позволяет
найти явную зависимость
dT от давления
(или объема) на изотерме.
Сохраняя в (36) лишь члены, включающие
d K 0/d
T, получим
0/d
T, получим
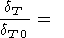 |
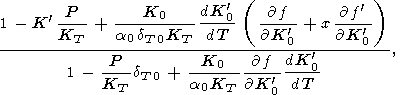 | (93) |
где
f обозначает
производную f по x.
обозначает
производную f по x.
 Эта формула обобщает
аналогичное соотношение Берча, которое следует из (93) при
dK
Эта формула обобщает
аналогичное соотношение Берча, которое следует из (93) при
dK 0/dT
= 0 [Birch, 1968].
Однако для обычных уравнений состояния
dT по
формуле Берча возрастает с
P (исключая уравнение Мурнагана,
для которого поведение
dT зависит от
знака разности
K
0/dT
= 0 [Birch, 1968].
Однако для обычных уравнений состояния
dT по
формуле Берча возрастает с
P (исключая уравнение Мурнагана,
для которого поведение
dT зависит от
знака разности
K - dT0 ).
Таким
образом, мы снова убеждаемся в том, что в анализе теплового
расширения с помощью (28) важно учитывать член с производной
dK
- dT0 ).
Таким
образом, мы снова убеждаемся в том, что в анализе теплового
расширения с помощью (28) важно учитывать член с производной
dK 0/dT.
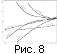
На рис. 8 показано несколько кривых
dT(x)
по (93) и уравнению
состояния (37), соответствующих кривым
a на рис. 1-3 (для
сравнения изображена прямая
dT = 6x
-1 по (47)).
Предпочтительным является значение
dK
0/dT.
На рис. 8 показано несколько кривых
dT(x)
по (93) и уравнению
состояния (37), соответствующих кривым
a на рис. 1-3 (для
сравнения изображена прямая
dT = 6x
-1 по (47)).
Предпочтительным является значение
dK 0/dT
0/dT 2
2 10-3
К-1 (см. раздел 2), а отклонения от него сильно влияют
на
значения
dT при сжатиях,
достигаемых в нижней мантии. При
высокой температуре для
dT имеем нижнюю
границу
dT > K
10-3
К-1 (см. раздел 2), а отклонения от него сильно влияют
на
значения
dT при сжатиях,
достигаемых в нижней мантии. При
высокой температуре для
dT имеем нижнюю
границу
dT > K - 1, согласно (42) [O. Anderson
et al., 1992a].
- 1, согласно (42) [O. Anderson
et al., 1992a].
Упругие модули и их
P-V-T производные - основа
термодинамики недр Земли [Birch, 1952, 1976;
Sumino and O. Anderson, 1984; D. Anderson,
1967,
1987, 1988, 1989;
O. Anderson et al., 1968, 1992a;
Duffy and D. Anderson, 1989;
Bina and Helffrich, 1992;
Duffy and Ahrens, 1992]. Они служат также параметрами
уравнений
состояния. Простейшие оценки адиабатического и изотермического
модулей сжатия при высоких давлениях получаются из их линейной
зависимости от давления, которая, однако, начинает заметно
завышать модули сжатия при приблизительно
x < 0.85. Изменение
производных модулей по давлению рассматривалось во многих
публикациях по уравнениям состояния (см. раздел 3). Для оценки
пригодности эмпирических уравнений состояния применяется связь
между первой
K
 (
( KT/
KT/ R)T и второй
K
R)T и второй
K

 (
( 2
KT/
2
KT/ P2)T производными
при
P = 0 [Pankov and Ullmann, 1979a;
Jeanloz, 1989;
O. Anderson, 1986; Hoffmeister, 1991b].
Обычно
K
P2)T производными
при
P = 0 [Pankov and Ullmann, 1979a;
Jeanloz, 1989;
O. Anderson, 1986; Hoffmeister, 1991b].
Обычно
K и
KK
и
KK
 для различных минералов при
P = 0 лежат в интервалах от 4 до 6 и от
- 5
до
- 10, соответственно.
Точность
(
для различных минералов при
P = 0 лежат в интервалах от 4 до 6 и от
- 5
до
- 10, соответственно.
Точность
( KS/
KS/ P)T (измеренных
с помощью ультразвуковых методов
или техники бриллюэновского рассеяния) составляет в лучшем
случае 1-5% (c учетом данных разных лаборатоий), а иногда 20 и
50%. Иногда для
K
P)T (измеренных
с помощью ультразвуковых методов
или техники бриллюэновского рассеяния) составляет в лучшем
случае 1-5% (c учетом данных разных лаборатоий), а иногда 20 и
50%. Иногда для
K и
K
и
K
 сообщаются аномально высокие значения
(cм. ссылки к таблицам в [Паньков и др., 1997]),
например,
K
сообщаются аномально высокие значения
(cм. ссылки к таблицам в [Паньков и др., 1997]),
например,
K = 5-7 (гранаты),
K
= 5-7 (гранаты),
K = 9-14 (пироксены),
KK
= 9-14 (пироксены),
KK
 = - 60 (шпинели), которые, как
предполагается, с ростом давления быстро принимают привычные
значения.
= - 60 (шпинели), которые, как
предполагается, с ростом давления быстро принимают привычные
значения.
Рассмотрим основные соотношения между адиабат-изотермическими производными модулей KS и KT. Переходя от переменных P, S к P, T, легко найти
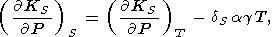 | (94) |
где
dS определено
формулой (82). Производная
( KS/
KS/ P)S характеризует
кривизну адиабаты и ударной адиабаты, имеющих касание второго
порядка. Далее из (16) находим
P)S характеризует
кривизну адиабаты и ударной адиабаты, имеющих касание второго
порядка. Далее из (16) находим
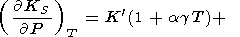 |
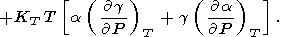 | (95) |
Исключая
( g
g P)T
с помощью (8) и (17) (или (122)) и используя (58),
получим
P)T
с помощью (8) и (17) (или (122)) и используя (58),
получим
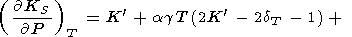 |
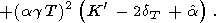 | (96) |
Подставляя сюда
( KS
KS P)T
из (94) и
dS из (93), приходим
к формуле
Берча [Birch, 1952]
P)T
из (94) и
dS из (93), приходим
к формуле
Берча [Birch, 1952]
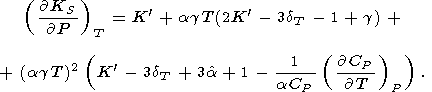 | (97) |
Различия между адиабат-изотермическими производными
KS и
KT обычно малы при нормальных условиях (1-2%
для мантийных
минералов). Из вычислений, в которых производная
( KS/
KS/ P)T использовалась
как входной параметр, мы находим
P)T использовалась
как входной параметр, мы находим
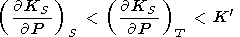 |
(исключая FeO,
для которого
( KS/
KS/ P)T плохо
известна
[Паньков и др., 1997]).
Однако Д. Андерсон [D. Anderson, 1989] указал на обратное
неравенство
P)T плохо
известна
[Паньков и др., 1997]).
Однако Д. Андерсон [D. Anderson, 1989] указал на обратное
неравенство
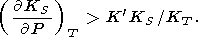 |
Для высокотемпературных оценок (таблица 3 и [Паньков и др., 1997]) произвольно было допущено
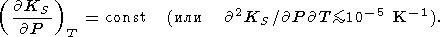 |
Отсюда по (94)-(97) были
найдены существенные различия, до 10-30%, между производными
KS и
KT по давлению при высокой температуре.
Фактически эти
различия того же порядка, что и приращения производной по
давлению за счет температуры. В частности, найденные
 2 KT/
2 KT/ P
P T составляют
3.5
T составляют
3.5 10-4 (стишовит),
2
10-4 (стишовит),
2 10-4 (ильменит),
3
10-4 (ильменит),
3 10-4 (Mg-перовскит),
1.7
10-4 (Mg-перовскит),
1.7 10-4 (MgO) и не
превышают
1
10-4 (MgO) и не
превышают
1 10-4 для других
минералов (некоторые оценки получились отрицательными).
10-4 для других
минералов (некоторые оценки получились отрицательными).
Для оценки
 2 KT
/
2 KT
/  P
P T Исаак [Isaak, 1993] использовал тождество
типа (91) и данные Белера по адиабатическому градиенту
температуры (см. также раздел 12.2). Он нашел
T Исаак [Isaak, 1993] использовал тождество
типа (91) и данные Белера по адиабатическому градиенту
температуры (см. также раздел 12.2). Он нашел
 2 KT/
2 KT/ P
P T = (3.9
T = (3.9 1.0)
1.0) 10-4 и
(3.3
10-4 и
(3.3 0.9)
0.9) 10-4
К-1 для MgO и оливина, соответственно. Кроме того, он
показал, что
эта производная уменьшается приблизительно на 30% при
изотермическом увеличении давления до 100 ГПа. Подобный
порядок величин в качестве нижней границы для этой производной
получен из ударноволновых данных [Duffy and Ahrens, 1992]
(cм.
также разделы 6 и 9).
10-4
К-1 для MgO и оливина, соответственно. Кроме того, он
показал, что
эта производная уменьшается приблизительно на 30% при
изотермическом увеличении давления до 100 ГПа. Подобный
порядок величин в качестве нижней границы для этой производной
получен из ударноволновых данных [Duffy and Ahrens, 1992]
(cм.
также разделы 6 и 9).
Дополнительно к этому анализу смешанных производных приведем следующее тождество
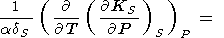 |
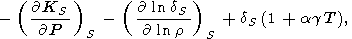 | (98) |
которое мы вывели из (94), используя (127) и
( g /
g / T)P из
(88).
Заметим, что аналогичное выражение, приведенное в статье [Bukowinsky and Wolf,
1990], отличается от (98) (вследствие либо опечатки, либо
ошибки). Для примера подставим в (98) характерные параметры для
нижней мантии:
(
T)P из
(88).
Заметим, что аналогичное выражение, приведенное в статье [Bukowinsky and Wolf,
1990], отличается от (98) (вследствие либо опечатки, либо
ошибки). Для примера подставим в (98) характерные параметры для
нижней мантии:
( KS/
KS/ P)S = 4,
agT =
0.1,
((
P)S = 4,
agT =
0.1,
(( lndS)/(
lndS)/( lnr ))S
= -1 и
dS = 3 при
x = 1 или
dS 2 при
x = 0.7. Отсюда находим
lnr ))S
= -1 и
dS = 3 при
x = 1 или
dS 2 при
x = 0.7. Отсюда находим
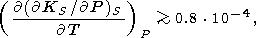 |
что вполне согласуется с предыдущими оценками.
При рассмотрении температурной зависимости KS и KT параметры Андерсона-Грюнайзена dS и dT представляются в виде (29) [D. Anderson et al., 1987; Duffy and D. Anderson, 1989; O. Anderson et al., 1992a]
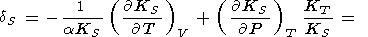 |
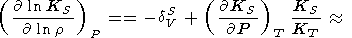 | (99) |
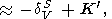 |
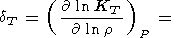 | (100) |
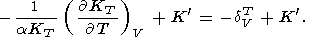 |
В разделе 9 мы рассмотрели основные закономерности
изменения
dS и
dT с давлением
и температурой (некоторое
уменьшение их с температурой в окрестности
T = 300 К,
стремление к постоянным значениям при
T > Q и убывание с
давлением). Теперь остановимся на вкладах собственных
dSV,
dTV
и внешних
K ангармонических
членов в (99) и (100).
ангармонических
членов в (99) и (100).
Д. Андерсон [D. Anderson, 1988, 1989]
подчеркнул, что
изменение модуля сжатия с температурой при
P = const в основном
связано с изменением
a, т.е. здесь внешний ангармонизм обычно
преобладает и усиливается с температурой (из-за роста
K
и далее, согласно (89) и (99),
Таким образом, при высоких температурах именно изотермический,
а не адиабатический модуль сжатия становится в основном фукцией
объема.
Анализируя термодинамические параметры нижней мантии, Д.
Андерсон [D. Anderson, 1987, 1988,
1989] опирался на данные
сейсмической томографии и геоида и предполагал, что наблюдаемые
горизонтальные аномалии вызваны вариациями температуры.
Стейси [Stacey, 1981] показал, что обьяснить эти аномалии
чисто
температурным эффектом нельзя, так при этом высоты геоида были
бы слишком велики. Поэтому предлагалось обьяснять сейсмические
неоднородности вариациями состава или даже частичным
плавлением в нижней мантии [Price et al., 1989;
Duffy and Ahrens,
1992b]. Тем не менее следуя Д. Андерсону, ниже мы приводим
оценки термодинамических параметров для нижней мантии,
рассматривая чисто температурный эффект формально как
предельный случай.
Модель Земли PREM, формула для акустического параметра
Грюнайзена и данные томографии дают на глубинах нижней мантии
(
Однако это значение
dSV
трудно согласовать с данными для
такого представительного минерала нижней мантии как периклаз.
Используя
dTV
= 0 и
dT = K
который применялся для оценок значений, приведенных в таблице 2 и
[Паньков и др., 1997].
Второй метод, предложенный в статье [O. Anderson, 1989]
и дополненный позже [О. Anderson et al., 1992], основан
на данных
для энтальпии. Здесь мы получим связь
KS с энтальпией, исходя из
формулы
g = aKS
V / CP,
которая дает производную
(
где звездочка означает величину при некоторой фиксированной
температуре. С помощью значений параметров из таблицы 2
и [Паньков и др., 1997] а также данных по энтальпии,
мы оценили
KS по (104) для ряда минералов. Энтальпийный
метод
оценки
KS является весьма эффективным: неопределенность
оценки
при высоких температурах составляет 2-5% (таблица 4). Ясно, что
оба метода дают более точные результаты при наличии
высокотемпературных значений
K
 ). Оценки,
приведенные в таблице 3 и [Паньков и др., 1997], показывают,
что при T = 300 К имеем
dTV<0
(исключая очень неопределенные
данные для FeO); большинство этих оценок попадает в интервал
между -1 и -2 (хотя для коэсита, стишовита и фиктивного Fe-перовскита
было найдено
dTV
= -17, -5 и -3.9, соответственно).
Согласно [D. Anderson, 1989], типичные значения
dTV
находятся в области от -4 до -1 (в таблице 5 указанной выше работы мы находим
также значения, выпадающие из этого интервала: 2.2
(ортопироксен),
- 5.3 (SrTiO
3 ) и
- 19 (СаСО
3 )).
Для 11 минералов из 54,
рассмотренных Д. Андерсоном, параметр
dSV
удовлетворяет
неравенству
|dSV|
> 2 (в частности,
dSV
= -4.1 (GeO
2 ), 3.8 (ортопироксен),
- 3.1
(SrTiO
3 ),
- 18 (CaCO
3 )). При высокой
температуре
dTV
может быть либо положительным, либо
отрицательным (между
- 1 и 1), а
|dSV|,
как правило, положительно и
находится в области 0-1.5 [Паньков и др., 1997]. Таким
образом, с
температурой
|dTV|
в среднем уменьшается,
а
|dSV|
возрастает. Вклад
dSV/dS в (99) обычно меньше
10-30% при 300 К и не превышает 15-60%
при высокой температуре, cоответственно,
dTV
да
). Оценки,
приведенные в таблице 3 и [Паньков и др., 1997], показывают,
что при T = 300 К имеем
dTV<0
(исключая очень неопределенные
данные для FeO); большинство этих оценок попадает в интервал
между -1 и -2 (хотя для коэсита, стишовита и фиктивного Fe-перовскита
было найдено
dTV
= -17, -5 и -3.9, соответственно).
Согласно [D. Anderson, 1989], типичные значения
dTV
находятся в области от -4 до -1 (в таблице 5 указанной выше работы мы находим
также значения, выпадающие из этого интервала: 2.2
(ортопироксен),
- 5.3 (SrTiO
3 ) и
- 19 (СаСО
3 )).
Для 11 минералов из 54,
рассмотренных Д. Андерсоном, параметр
dSV
удовлетворяет
неравенству
|dSV|
> 2 (в частности,
dSV
= -4.1 (GeO
2 ), 3.8 (ортопироксен),
- 3.1
(SrTiO
3 ),
- 18 (CaCO
3 )). При высокой
температуре
dTV
может быть либо положительным, либо
отрицательным (между
- 1 и 1), а
|dSV|,
как правило, положительно и
находится в области 0-1.5 [Паньков и др., 1997]. Таким
образом, с
температурой
|dTV|
в среднем уменьшается,
а
|dSV|
возрастает. Вклад
dSV/dS в (99) обычно меньше
10-30% при 300 К и не превышает 15-60%
при высокой температуре, cоответственно,
dTV
да
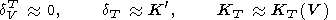
(101) 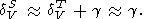
(102) 10.2. Интерпретация данных сейсмической томографии
 KS/
KS/ P)S =
3-3.8,
g = 1.2
P)S =
3-3.8,
g = 1.2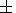 0.1 и
dS = 1-1.8. Следовательно,
(89), (94), (96), (99)
и (100) приводят к
dT
0.1 и
dS = 1-1.8. Следовательно,
(89), (94), (96), (99)
и (100) приводят к
dT dS
+ g = 2.2-3.0,
K
dS
+ g = 2.2-3.0,
K = 3-3.8 (небольшая
поправка может быть введена с помощью формулы
a = a0
xdT
при
a0 = 4
= 3-3.8 (небольшая
поправка может быть введена с помощью формулы
a = a0
xdT
при
a0 = 4 10-5 К-1 и
T
10-5 К-1 и
T 2000-3000 К),
dSV
2000-3000 К),
dSV K
K - dS = 1.2-2.8
и
dTV
= dSV
- g = -0.1-1.7.
Если для
g допустить большую неопределенность, скажем
- dS = 1.2-2.8
и
dTV
= dSV
- g = -0.1-1.7.
Если для
g допустить большую неопределенность, скажем
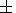 0.4,
то
dT
0.4,
то
dT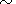 1.9-3.3 и
dSV
1.9-3.3 и
dSV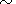 - 0.4-2.0.
Таким образом, внешние ангармонические
эффекты, хотя и ослабевают с давлением, все еще
преобладают в
нижней мантии ( K
- 0.4-2.0.
Таким образом, внешние ангармонические
эффекты, хотя и ослабевают с давлением, все еще
преобладают в
нижней мантии ( K > dSV
или
|dTV| ).
Член от собственного ангармонизма
dSV
заметно возрастает с давлением, но его аналог
dTV
может либо
возрастать, либо убывать, достигая нуля. Д. Андерсон [D. Anderson,
1989],
ссылаясь на экспериментальную информацию, особо
подчеркнул случай с
dTV
> dSV
или
|dTV| ).
Член от собственного ангармонизма
dSV
заметно возрастает с давлением, но его аналог
dTV
может либо
возрастать, либо убывать, достигая нуля. Д. Андерсон [D. Anderson,
1989],
ссылаясь на экспериментальную информацию, особо
подчеркнул случай с
dTV 0, откуда
dSV
0, откуда
dSV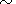 g = 1.2.
g = 1.2. 
 3.2-3.5
при
x = 0.7 из уравнения Берча-Мурнагана для MgO, мы находим
dS
3.2-3.5
при
x = 0.7 из уравнения Берча-Мурнагана для MgO, мы находим
dS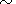 dT
- g = 2.2-2.5 при
g = g0x
( q = 1, см. (119)). Эти значения
dT и
dS в среднем все
еще заметно
превышают сейсмические оценки. О. Андерсон и др. [O. Anderson et al.,
1992b] указали, что данные для MgO можно согласовать
с сейсмическими выводами, если допустить
q < 1. В частности, наш
анализ показывает, что допустима следующая согласованная
совокупность значений:
dTV
0.2,
q 0.8,
g = g0xq
1.1 (при
x = 0.7 ) и
dT = K
dT
- g = 2.2-2.5 при
g = g0x
( q = 1, см. (119)). Эти значения
dT и
dS в среднем все
еще заметно
превышают сейсмические оценки. О. Андерсон и др. [O. Anderson et al.,
1992b] указали, что данные для MgO можно согласовать
с сейсмическими выводами, если допустить
q < 1. В частности, наш
анализ показывает, что допустима следующая согласованная
совокупность значений:
dTV
0.2,
q 0.8,
g = g0xq
1.1 (при
x = 0.7 ) и
dT = K - dTV
3-3.3 и
dS 1.9-2.2. Во
всяком случае, на этом пути
можно искать согласия с сейсмическими данными, если бы значения,
выведенные из томографии, основывались на чисто температурном
объяснении сейсмических аномалий
- dTV
3-3.3 и
dS 1.9-2.2. Во
всяком случае, на этом пути
можно искать согласия с сейсмическими данными, если бы значения,
выведенные из томографии, основывались на чисто температурном
объяснении сейсмических аномалий
10.3. Оценки KS при высокой температуре
10.3.1.
Мы дополним анализ зависимости
K<UNDEF>S от
температуры при
Р =0 рассмотрением двух методов.
Один из них использует условие
dS = d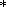 S =
const [D. Anderson, 1988; Duffy and D. Anderson,
1989],
откуда, в силу (99), имеем степенной закон
S =
const [D. Anderson, 1988; Duffy and D. Anderson,
1989],
откуда, в силу (99), имеем степенной закон
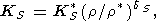
(103)  KS/
KS/ H)P. Таким
образом,
H)P. Таким
образом,
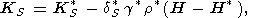
(104) 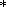 S,
r
S,
r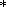 ,
g
,
g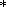 ,
H
,
H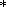 , d
, d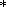 S.
S. 10.3.2.

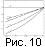 В заключение этого анализа приведем зависимость
KS(T) при
P = 0, рассчитанную из уравнения состояния Ми-Грюнайзена
с
g = g0xq
для трех минералов (рис. 9).
Из сравнения кривых
KS при разных
q = 0-2 с экспериментальными данными
(рис. 10) можно получить подходящие значения
q, но учитывая
результаты, приведенные для этих же уравнений состояния в
разделах 6 и 7, не всегда удается найти
такие значения
q, при
которых уравнение состояния одновременно согласовывалось бы с
данными по
a, CP,
t и
KS. Это, как и в разделах 6 и 7,
свидетельствует о неточности тепловой части уравнения Ми-Грюнайзена.
В заключение этого анализа приведем зависимость
KS(T) при
P = 0, рассчитанную из уравнения состояния Ми-Грюнайзена
с
g = g0xq
для трех минералов (рис. 9).
Из сравнения кривых
KS при разных
q = 0-2 с экспериментальными данными
(рис. 10) можно получить подходящие значения
q, но учитывая
результаты, приведенные для этих же уравнений состояния в
разделах 6 и 7, не всегда удается найти
такие значения
q, при
которых уравнение состояния одновременно согласовывалось бы с
данными по
a, CP,
t и
KS. Это, как и в разделах 6 и 7,
свидетельствует о неточности тепловой части уравнения Ми-Грюнайзена.
This document was generated by TeXWeb
(Win32, v.1.0) on August 10, 1998.