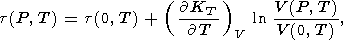Термодинамика глубинных геофизических сред
В. Паньков, В. Ульман, Р. Хайнрих, Д. Краке
7. Теплоемкость
Решеточная теплоемкость минералов при
T 1000 K близка к
классическому пределу
3Rn = 3RM/m (молярное значение,
где
R -
газовая постоянная,
n - число атомов в химической формуле). Из
калориметрии мы имеем информацию об изобарической
теплоемкости
CP при
P = 0, которая превосходит
CV на 1-3%
при 300 К и 10-15% при
T > Q (таблица 2 и [Паньков и др.,
1997]).
Так как для мантийных минералов
m 20-22,
классическое
значение
CV равно 1.13-1.25 Дж/г К. Ангармонические
высокотемпературные поправки в
CV становятся существенными,
в зависимости от минерала, либо вблизи
точки плавления, либо уже при комнатной температуре (иногда при
T более 1/6 температуры плавления) [Mulargia and Boschi, 1980;
Quareni and Mulargia, 1988; Reynard et al.,
1992;
Fiquet et al., 1992].
20-22,
классическое
значение
CV равно 1.13-1.25 Дж/г К. Ангармонические
высокотемпературные поправки в
CV становятся существенными,
в зависимости от минерала, либо вблизи
точки плавления, либо уже при комнатной температуре (иногда при
T более 1/6 температуры плавления) [Mulargia and Boschi, 1980;
Quareni and Mulargia, 1988; Reynard et al.,
1992;
Fiquet et al., 1992].
7.1. P- V- T
производные теплоемкости
Из тождеств
 2E/
2E/ V
V T =
T =  2E/
2E/  T
T V и
V и
 2S/
2S/ P
P T =
T =  2S/
2S/ T
T P,
используя соотношения Максвелла, имеем
P,
используя соотношения Максвелла, имеем
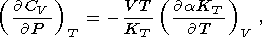 | (57) |
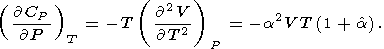 | (58) |
Заметим, что (57) и (58) - лишь варианты тождеств (33) и (34),
соответственно. Логарифмические производные по объему
при
T = const можно выразить следующим образом
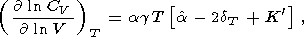 | (59) |
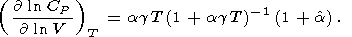 | (60) |
Эти тождества использованы для расчета производных,
приведенных
в таблицах 2 и 3, а также в [Паньков и др., 1997]. О.
Андерсон и др.
[O. Anderson et al., 1993] отметили, что в дебаевской
модели
( CV/
CV/ P)T 0,
и тогда
a 2dT
- K
P)T 0,
и тогда
a 2dT
- K .
.
Разность
CP - CV
удовлетворяет тождеству
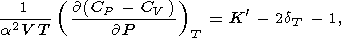 | (61) |
т.е. убывает с давлением при обычных значениях
K и
dT (таблица 3,
[Паньков и др., 1997]).
и
dT (таблица 3,
[Паньков и др., 1997]).
Берч [Birch, 1952] оценил уменьшение
CP с давлением в
нижней мантии, полагая
a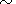 4 и
agT
4 и
agT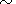 0.1,
что, по степенному закону для
CP, дает
13-16% уменьшение
CP на изотерме в области
x от 1.0 до 0.7.
Согласно Берчу, максимальное уменьшение
CP в мантии, по-видимому,
не превышает 20%.
0.1,
что, по степенному закону для
CP, дает
13-16% уменьшение
CP на изотерме в области
x от 1.0 до 0.7.
Согласно Берчу, максимальное уменьшение
CP в мантии, по-видимому,
не превышает 20%.
Адиабатическая производная
CP по объему
равна
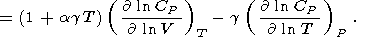 | (62) |
Подставляя
( ln CP/
ln CP/ ln T)P
ln T)P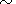 0.15 (типичное значение для минералов при
T 1000 К),
g
0.15 (типичное значение для минералов при
T 1000 К),
g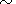 1-1.5,
agT
1-1.5,
agT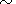 0.1 и
(
0.1 и
( ln CP/
ln CP/ ln V)T
ln V)T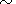 0.5 (для
a
0.5 (для
a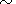 4 ),
мы находим
(
4 ),
мы находим
(  ln CP
ln CP ln V)S
ln V)S 0.3-0.4.
Следовательно, уменьшение
CP в нижней мантии (до
x
0.3-0.4.
Следовательно, уменьшение
CP в нижней мантии (до
x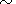 0.7 )
по степенному закону составит 8-13%.
0.7 )
по степенному закону составит 8-13%.
Используя (29), представим производную
CP по температуре в
виде
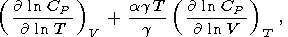 | (63) |
Второй член, происходящий от внешнего ангармонизма, можно
оценить с помощью (58), так что (63) и данные по
( CP/
CP/ T)P дают
сведения о первом члене, связанном с собственным ангармонизмом.
При комнатной температуре
(
T)P дают
сведения о первом члене, связанном с собственным ангармонизмом.
При комнатной температуре
( ln CP/
ln CP/ ln V)T
порядка
(
ln V)T
порядка
( ln CP/
ln CP/ ln T)P, но тем не
менее вклад второго члена в сумму мал из-за множителя
agT.
При
высокой температуре этот вклад возрастает обычно до 15-30%
(60-70% для ильменита и перовскита) [Паньков и др., 1997].
В
классическом пределе
CV = const, и если положить
a
ln T)P, но тем не
менее вклад второго члена в сумму мал из-за множителя
agT.
При
высокой температуре этот вклад возрастает обычно до 15-30%
(60-70% для ильменита и перовскита) [Паньков и др., 1997].
В
классическом пределе
CV = const, и если положить
a a
(V) и
g
a
(V) и
g g
(V), то
(
g
(V), то
( CP/
CP/ T)V
T)V agCV.
agCV.
Далее, из (17) и (18) легко найти тождество
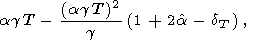 | (64) |
которое использовано в расчетах этой производной
для минералов
таблицы 3 и в работе [Паньков и др., 1997]. Затем с помощью
тождества
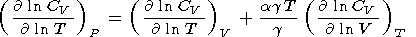 | (65) |
можно вычислить
(( ln CV)/(
ln CV)/( ln T))V,
располагая оценками второго члена по (59).
ln T))V,
располагая оценками второго члена по (59).
Явная зависимость
CV (V, T) может быть получена
из моделей и
измерений колебательного спектра твердых
тел [напр., Pitzer and Brewer, 1961]
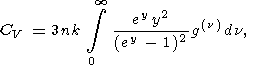 | (66) |
где
k - постоянная Больцмана,
y = hnkT,
g (n) - спектральная плотность,
n - решеточные частоты,
включая оптические и акустические моды
[Kieffer, 1979a, 1979b, 1979c,
1980;
Hofmeister, 1991a, 1991b;
Richet et al., 1992].
Этот метод дает информацию о неточности
теории Дебая и
соответствующего приближения
g = - d ln Q/d
ln V. В теории Дебая
характеристическая температура
Q обычно оценивается по
акустическим данным, но
Q, найденное по данным для
CV при
T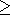 300 К
(обозначаемое
Qth ) в среднем
превышает акустическое
Q (Qa)
на
20% (большие отклонения свойственны кварцу и коэситу) (см.
таблицу 2, а также [Паньков и др., 1997; Watanabe,
1982]).
Однако Шопла [Chopelas, 1990b] нашла хорошее
согласие дебаевской
модели с данными спектра для MgO при давлениях до 200 кбар при
условии
Q
300 К
(обозначаемое
Qth ) в среднем
превышает акустическое
Q (Qa)
на
20% (большие отклонения свойственны кварцу и коэситу) (см.
таблицу 2, а также [Паньков и др., 1997; Watanabe,
1982]).
Однако Шопла [Chopelas, 1990b] нашла хорошее
согласие дебаевской
модели с данными спектра для MgO при давлениях до 200 кбар при
условии
Q Vg, т.е.
q = 0.
Vg, т.е.
q = 0.
Спектроскопические измерения при высоких давлениях
позволяют найти производную
( CV/
CV/ P)T. Так,
данные до 200 кбар
[Chopelas, 1990a, 1990b] показывают,
что
CV линейно уменьшается
с
P с градиентом
- (
P)T. Так,
данные до 200 кбар
[Chopelas, 1990a, 1990b] показывают,
что
CV линейно уменьшается
с
P с градиентом
- ( CV/
CV/ P)T =
17.6
P)T =
17.6 10-3 (T
= 300 К) и
0.91
10-3 (T
= 300 К) и
0.91 10-3 (T
= 1800 К) для MgO и
49.8
10-3 (T
= 1800 К) для MgO и
49.8 10-3 (T
= 300 К) и
3.4
10-3 (T
= 300 К) и
3.4 10-3 (T =
1800 К) Дж/моль К
кбар для форстерита. Если с этим значением экстраполировать
CV до
максимального давления в мантии
P = 1357 кбар, то
CV уменьшится
на 40-60%, 8-12% и 2-3% на изотермах
T = 300 К, 1000 К и 1700 К, соответственно.
Сравнивая эти результаты с приведенными выше
оценками убывания
CP, мы заключаем, что разность
CP - CV
в нижней мантии должна быть чрезвычайно мала. Из данных Шоплы,
используя также
KT и
CV из таблицы 2, мы найдем
(
10-3 (T =
1800 К) Дж/моль К
кбар для форстерита. Если с этим значением экстраполировать
CV до
максимального давления в мантии
P = 1357 кбар, то
CV уменьшится
на 40-60%, 8-12% и 2-3% на изотермах
T = 300 К, 1000 К и 1700 К, соответственно.
Сравнивая эти результаты с приведенными выше
оценками убывания
CP, мы заключаем, что разность
CP - CV
в нижней мантии должна быть чрезвычайно мала. Из данных Шоплы,
используя также
KT и
CV из таблицы 2, мы найдем
( ln CV
/
ln CV
/ ln V)T
= 0.77 (T = 300 К) и
0.022 (T = 1800 К) для MgO и 0.54 ( T = 300 К ) и 0.022 ( T = 1700 К ) для форстерита.
Эти результаты сравнимы с нашими оценками по термодинамическим данным
(таблица 3).
ln V)T
= 0.77 (T = 300 К) и
0.022 (T = 1800 К) для MgO и 0.54 ( T = 300 К ) и 0.022 ( T = 1700 К ) для форстерита.
Эти результаты сравнимы с нашими оценками по термодинамическим данным
(таблица 3).
7.2. Явная зависимость CP от температуры при P = 0.
Калориметрические данные для
CP в зависимости от
температуры при
P = 0 обычно сглаживают с помощью различных
эмпирических выражений [напр., Fei and Saxena, 1987;
Berman, 1988; Saxena, 1989;
Richet and Fiquet, 1991]
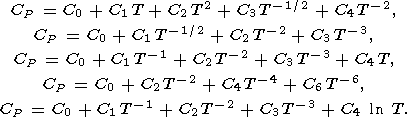 | (67) |
 Рише и Фике [Richet and Fiquet, 1991] показали, что
последняя из
этих формул предпочтительна, но ни одна из них не является
достаточной для описания данных в широкой области температур.
На рис. 6 иллюстрируется также зависимость
CP (T) по формуле,
использованной в [Watanabe, 1982], где приведены измерения
CP в
области температур 350-700 К. Как показывает пример MgO,
экстраполяция
CP по этой формуле не всегда приемлема.
Рише и Фике [Richet and Fiquet, 1991] показали, что
последняя из
этих формул предпочтительна, но ни одна из них не является
достаточной для описания данных в широкой области температур.
На рис. 6 иллюстрируется также зависимость
CP (T) по формуле,
использованной в [Watanabe, 1982], где приведены измерения
CP в
области температур 350-700 К. Как показывает пример MgO,
экстраполяция
CP по этой формуле не всегда приемлема.
Так же как в анализе теплового расширения (раздел 6.3), мы
вычислили
CP (T) при
P = 0 для трех минералов из того же уравнения
состояния, которое использовалось в разделе 6.3 для расчета
a.
Результаты этих вычислений приведены на рис. 6. Видно, что,
варьируя параметр
q в пределах 1-2, можно добиться согласия с
приведенными на рисунке данными. Отсюда, в частности, мы
находим
q 0 для MgO,
q = 1-2 для Al
2 O
3 и
q
0 для MgO,
q = 1-2 для Al
2 O
3 и
q 0.5 для форстерита. Однако эти значения
q не всегда удается согласовать
с данными по
a (раздел 6.3), что снова указывает на неточность
используемой
модели уравнения состояния Ми-Грюнайзена.
0.5 для форстерита. Однако эти значения
q не всегда удается согласовать
с данными по
a (раздел 6.3), что снова указывает на неточность
используемой
модели уравнения состояния Ми-Грюнайзена.
8. Тепловое давление
8.1. P- V- T
производные термического коэффициента давления
Термический коэффициент давления (9), (12) - основная
характеристика теплового давления и может быть определен как
t = ( Pth/
Pth/ T)V.
Заметим, что
t имеет также смысл скрытой теплоты расширения
на 1 К. Особенно большое внимание этому параметру уделили О.
Андерсон и сотрудники [O. Anderson, 1982, 1984,
1988;
O. Anderson and Sumino, 1980;
O. Anderson and Goto, 1989; О. Anderson
et al., 1982,
1991, 1992a],
в частности, в связи с их разработкой
резонансного метода для измерения упругих свойств минералов при
высоких температурах.
T)V.
Заметим, что
t имеет также смысл скрытой теплоты расширения
на 1 К. Особенно большое внимание этому параметру уделили О.
Андерсон и сотрудники [O. Anderson, 1982, 1984,
1988;
O. Anderson and Sumino, 1980;
O. Anderson and Goto, 1989; О. Anderson
et al., 1982,
1991, 1992a],
в частности, в связи с их разработкой
резонансного метода для измерения упругих свойств минералов при
высоких температурах.
Основные тождества для производных
t легко вывести из тех,
что уже приводились в разделах 6 и 7. Особенно полезны
следующие тождества [Brennan and Stacey, 1979;
Birch, 1978; O. Anderson and Yamamoto, 1987]
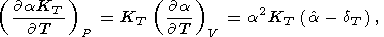 | (68) |
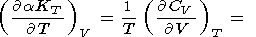 | (69) |
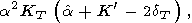 |
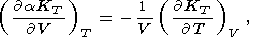 | (70) |
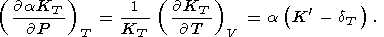 | (71) |
Первая из этих формул получается путем раскрытия производной
слева и использования (30), вторая, (69) - следствие (57), формулу
(70) легко вывести, приравнивая производные
P по
V и
T, взятые в
том или ином порядке, а (71) - следствие (70) и (31).
Из (68) и (69) также имеем
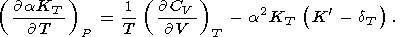 | (72) |
Согласно (71), при обычном соотношении
dT > K параметр
t убывает с давлением на изотерме.
Однако при высоких давлениях это
убывание может смениться ростом
t, как это имеет место в модели
PIB MgO [O. Anderson et al., 1993]. Из (68) ясно, что
t, по крайней
мере при
T < Q, растет с температурой на изохоре.
параметр
t убывает с давлением на изотерме.
Однако при высоких давлениях это
убывание может смениться ростом
t, как это имеет место в модели
PIB MgO [O. Anderson et al., 1993]. Из (68) ясно, что
t, по крайней
мере при
T < Q, растет с температурой на изохоре.
Логарифмическая производная
t по температуре при
P = const, согласно (29), представляется в виде
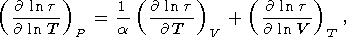 | (73) |
где первый член (эффект собственного ангармонизма),
положительный в силу (69), можно написать как сумму
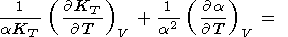 | (74) |
а второй, с учетом (70) и (71), равен
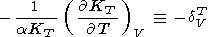 | (75) |
где введено обозначение
dTV
(см. дальнейший анализ в разделе 9).
Хотя член от собственного ангармонизма в (73) доминирует при
T < Q из-за больших значений
a, знак (73) при высоких температурах
может быть любым.
Температурная зависимость
t похожа на аналогичную
зависимость
CV, так что при
T > Q величина
t стремится быть
независящей от температуры [O. Anderson, 1984]. Соответственно,
тепловое давление
Pth стремится к линейной зависимости от
T. Наши
оценки
t (таблица 3, см. также [Паньков и др.,
1997]) показывают,
что нелинейные члены в
Pth дают вклад не более 1-3% при
максимальных температурах, указанных в таблице 3 и [Паньков и др., 1997].
Линейность
Pth по
T в высокотемпературной области
считается универсальным свойством твердых
тел [Anderson et al., 1992a].
В отличие от температурной зависимости, степень
зависимости
t от обь
e ма при
T = const варьирует с переходом от одного типа материалов к другому.
Согласно Андерсону и др.,
земные материалы попадают в промежуточную группу между
минералами с существенной зависимостью
t от объема
(например, золото) и веществами со сравнительно слабой зависимостью
t (V) (например, NaCl, щелочные металлы,
благородные элементы).
Существенно, что эти выводы были сделаны на основе как
P-V-T данных
(анализ
Pth (V,T) ), так и высокотемпературных
данных для
KT и
aKT при
P = 0 (анализ (70)).
На первый взгляд, наблюдаемая закономерность в
t (T) при
T > Q обьясняется тем, что в этой области
температур
CV const,
а, следовательно,
g не зависит от температуры в виду (8) и (69).
Другими словами, при высоких температурах оправдывается
квазигармоническое уравнение состояния Ми-Грюнайзена. Однако
это не совсем так в общем случае, если исходить из условий
t = const или
t = t (V)
, которые совместимы со случаем
CV (T) (см. (69)) и,
следовательно, с зависимостью
g как от объема,
так и от
температуры [O. Anderson and Yamamoto, 1987]. C теоретической
точки зрения, отклонение
CV от закона Дюлонга и Пти [напр.,
Mulargia and Broccio, 1983; O. Anderson and Suzuki,
1983;
Gillet et al., 1991; Reynard et al., 1992]
частично связано с собственным
ангармонизмом, описываемым членами третьего и последующих
порядков в разложении решеточного гамильтониана. При описании
экспериментальных данных термическое уравнение состояния
обычно требует сохранения меньшего числа членов этого
разложения, чем калорическое уравнение состояния [Leibfried and Ludwig, 1961; Wallace, 1972;
Davies, 1973]. Таким
образом, наблюдаемое отсутствие ангармонизма в
Pth с ростом
T и
выраженная зависимость
g от
T могут указывать на то, что либо
квазигармонический предел для колебательного
g еще не достигнут,
либо члены высшего порядка в тепловой части уравнения состояния
взаимно компенсируются [O. Anderson et al., 1982].
const,
а, следовательно,
g не зависит от температуры в виду (8) и (69).
Другими словами, при высоких температурах оправдывается
квазигармоническое уравнение состояния Ми-Грюнайзена. Однако
это не совсем так в общем случае, если исходить из условий
t = const или
t = t (V)
, которые совместимы со случаем
CV (T) (см. (69)) и,
следовательно, с зависимостью
g как от объема,
так и от
температуры [O. Anderson and Yamamoto, 1987]. C теоретической
точки зрения, отклонение
CV от закона Дюлонга и Пти [напр.,
Mulargia and Broccio, 1983; O. Anderson and Suzuki,
1983;
Gillet et al., 1991; Reynard et al., 1992]
частично связано с собственным
ангармонизмом, описываемым членами третьего и последующих
порядков в разложении решеточного гамильтониана. При описании
экспериментальных данных термическое уравнение состояния
обычно требует сохранения меньшего числа членов этого
разложения, чем калорическое уравнение состояния [Leibfried and Ludwig, 1961; Wallace, 1972;
Davies, 1973]. Таким
образом, наблюдаемое отсутствие ангармонизма в
Pth с ростом
T и
выраженная зависимость
g от
T могут указывать на то, что либо
квазигармонический предел для колебательного
g еще не достигнут,
либо члены высшего порядка в тепловой части уравнения состояния
взаимно компенсируются [O. Anderson et al., 1982].
Подводя итог анализу
t, сформулируем следующие
утверждения и их следствия. 1) Пусть
CV не зависит от
V,
т.е. либо
CV = CV
(T), либо
CV = const.
2) Пусть
KT = KT
(V), что равносильно
dT = K .
Из 1) следует, что либо
t = t (V)
, либо
t = const,
и далее
KT - либо линейная
функция температуры, либо
KT (V), что ведет к
q = q (V) (или
q = 1 ),
g = Vt
(V)/CV (T) или
g = g (V).
Аналогично утверждение
2) равносильно либо
t = t (T), либо
t = const.
Если оба утверждения 1), но с
CV const, и 2)
одновременно выполняются, то
t = const,
g = const
.
Из 1) следует, что либо
t = t (V)
, либо
t = const,
и далее
KT - либо линейная
функция температуры, либо
KT (V), что ведет к
q = q (V) (или
q = 1 ),
g = Vt
(V)/CV (T) или
g = g (V).
Аналогично утверждение
2) равносильно либо
t = t (T), либо
t = const.
Если оба утверждения 1), но с
CV const, и 2)
одновременно выполняются, то
t = const,
g = const V/CV
(T) и
q = 1. Условие
CV = сonst и
KT = KT
(V) приводят к
g = const
V/CV
(T) и
q = 1. Условие
CV = сonst и
KT = KT
(V) приводят к
g = const V.
V.
8.2. Модели теплового давления
Термическое уравнение состояния, получающееся
непосредственно путем интегрирования (12), имеет вид
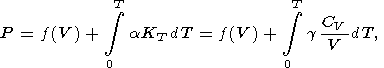 | (76) |
где
f (V) - давление статической решетки плюс давление нулевых
колебаний. Второй член - полное тепловое давление
Pth,
учитывающее все ангармонические вклады. Это уравнение можно
переписать в виде
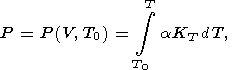 | (77) |
где, например,
T0 = 300 К. Тепловое давление, в соответствии с
описанным выше поведением
t, приближенно записывается как
[O. Anderson, 1988, 1989]
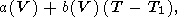 | (78) |
где
T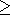 T1
T1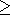 Q. Как уже отмечалось,
для определенного класса
твердых тел зависимостью от
V в (78) можно пренебречь.
Q. Как уже отмечалось,
для определенного класса
твердых тел зависимостью от
V в (78) можно пренебречь.
В уравнении Ми-Грюнайзена, однако, тепловое давление
определяется выражением
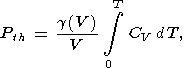 | (79) |
где используется квазигармоническая теплоемкость
CV. Таким
образом, здесь при высоких температурах
T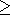 T2
T2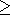 Q,
когда
CV
Q,
когда
CV const,
const,
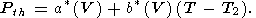 | (80) |
Даже если
b (V) = b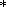 (V) в некоторой области температур, различие
между (78) и (80) не исчезает, так как в общем случае
g = g (V,T)
в (78) и
a
(V) в некоторой области температур, различие
между (78) и (80) не исчезает, так как в общем случае
g = g (V,T)
в (78) и
a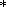 a. Практичеки
же для определенных минералов и при
современной точности измерений
Pth по (78) и теории Ми-Грюнайзена
могут быть не отличимы [Fei et al., 1992;
Mao et al., 1991], особенно для минералов с низкой
дебаевской температурой.
a. Практичеки
же для определенных минералов и при
современной точности измерений
Pth по (78) и теории Ми-Грюнайзена
могут быть не отличимы [Fei et al., 1992;
Mao et al., 1991], особенно для минералов с низкой
дебаевской температурой.
Член
Pth в (77) можно аппроксимировать несколькими
способами. Так, задаваясь объемными зависимостями
K и
dT и интегрируя
(75), можно найти
t (V) при
T = const [О. Anderson et al., 1992a, 1993].
Затем зависимость
t от температуры выводится из данных для
a (T) и
KT (T) при
P = 0. Другую возможность такой
аппроксимации дает степенной закон для
t (V) на изотерме.
и
dT и интегрируя
(75), можно найти
t (V) при
T = const [О. Anderson et al., 1992a, 1993].
Затем зависимость
t от температуры выводится из данных для
a (T) и
KT (T) при
P = 0. Другую возможность такой
аппроксимации дает степенной закон для
t (V) на изотерме.
Фай и др. [Fei et al., 1992a, 1992b]
и Мао и др.
[Mao et al., 1991] использовали ряд моделей
Pth для описания
рентгеновских
P-V-T данных. В одной
из моделей они допустили
( KT/
KT/ T)V =
const.
В этом случае (70) дает
T)V =
const.
В этом случае (70) дает
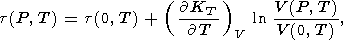 | (81) |
где
t (0, T) определяется по данным для
a при условии
(d KTd
T)P = const,
причем последнее допускалось во всей области
P-V-T измерений.
Из постоянства обеих температурных производных
KT следует,
что
tK = const, но тогда
K
= const, но тогда
K будет расти
с давлением на
изотерме и убывать с температурой на изобаре, что расходится с
обычным поведением этого параметра (см. раздел 6).
Отметим, что параметр
dT может быть
очень чувствителен к
принимаемой модели
Pth [Mao et al., 1991],
хотя величины
Pth по разным моделям могут быть близки.
будет расти
с давлением на
изотерме и убывать с температурой на изобаре, что расходится с
обычным поведением этого параметра (см. раздел 6).
Отметим, что параметр
dT может быть
очень чувствителен к
принимаемой модели
Pth [Mao et al., 1991],
хотя величины
Pth по разным моделям могут быть близки.
 Наконец, на рис. 7 мы иллюстрируем зависимость
t от
температуры при
P = 0, вычисленную из уравнения Ми-Грюнайзена,
описанного в разделе 6, для периклаза, корунда и
форстерита с различными значениями
q в интервале 0-2. Хотя это
уравнение дает правильные закономерности
изменения и порядок
величины
t, трудно добиться полного согласия с приведенными
данными, как и в случаях с теплоемкостью
(раздел 7) и тепловым
расширением (раздел 6). Несомненно требуется большая точность
определения теплового давления, чем дает
уравнение Ми-Грюнайзена
(например, для расчетов фазовых диаграмм, когда 10%
ошибка в
Pth существенно влияет на рассчитываемые
фазовые кривые).
Наконец, на рис. 7 мы иллюстрируем зависимость
t от
температуры при
P = 0, вычисленную из уравнения Ми-Грюнайзена,
описанного в разделе 6, для периклаза, корунда и
форстерита с различными значениями
q в интервале 0-2. Хотя это
уравнение дает правильные закономерности
изменения и порядок
величины
t, трудно добиться полного согласия с приведенными
данными, как и в случаях с теплоемкостью
(раздел 7) и тепловым
расширением (раздел 6). Несомненно требуется большая точность
определения теплового давления, чем дает
уравнение Ми-Грюнайзена
(например, для расчетов фазовых диаграмм, когда 10%
ошибка в
Pth существенно влияет на рассчитываемые
фазовые кривые).
This document was generated by TeXWeb
(Win32, v.1.0) on August 10, 1998.
 20-22,
классическое
значение
CV равно 1.13-1.25 Дж/г К. Ангармонические
высокотемпературные поправки в
CV становятся существенными,
в зависимости от минерала, либо вблизи
точки плавления, либо уже при комнатной температуре (иногда при
T более 1/6 температуры плавления) [Mulargia and Boschi, 1980;
Quareni and Mulargia, 1988; Reynard et al.,
1992;
Fiquet et al., 1992].
20-22,
классическое
значение
CV равно 1.13-1.25 Дж/г К. Ангармонические
высокотемпературные поправки в
CV становятся существенными,
в зависимости от минерала, либо вблизи
точки плавления, либо уже при комнатной температуре (иногда при
T более 1/6 температуры плавления) [Mulargia and Boschi, 1980;
Quareni and Mulargia, 1988; Reynard et al.,
1992;
Fiquet et al., 1992].
 2E/
2E/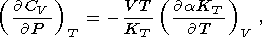
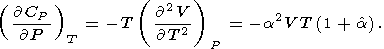
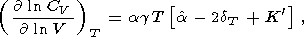
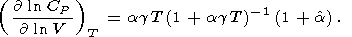
 .
. 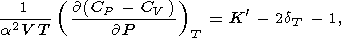
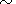 4 и
agT
4 и
agT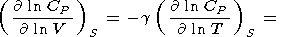
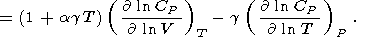
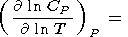
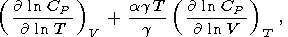
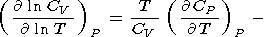
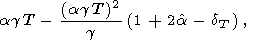
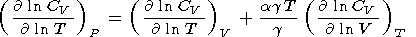
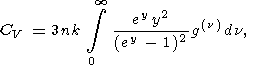
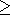 300 К
(обозначаемое
Qth ) в среднем
превышает акустическое
Q (Qa)
на
20% (большие отклонения свойственны кварцу и коэситу) (см.
таблицу 2, а также [Паньков и др.,
300 К
(обозначаемое
Qth ) в среднем
превышает акустическое
Q (Qa)
на
20% (большие отклонения свойственны кварцу и коэситу) (см.
таблицу 2, а также [Паньков и др.,  10-3 (T
= 300 К) и
0.91
10-3 (T
= 300 К) и
0.91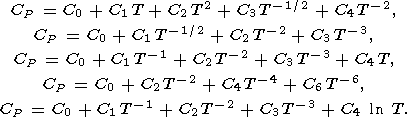

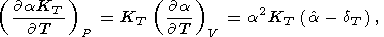
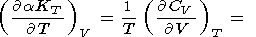
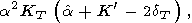
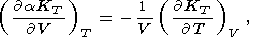
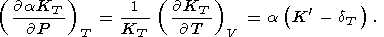
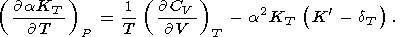
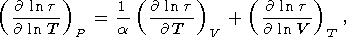
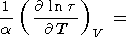
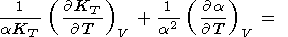
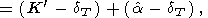
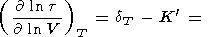
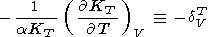
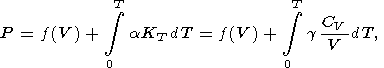
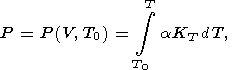
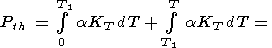
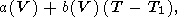
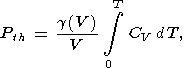
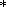 (V) в некоторой области температур, различие
между (78) и (80) не исчезает, так как в общем случае
g = g (V,T)
в (78) и
a
(V) в некоторой области температур, различие
между (78) и (80) не исчезает, так как в общем случае
g = g (V,T)
в (78) и
a