6. Коэффициент теплового расширения

6.1. P-T производные

Из тождества ² V/ T P = ² V/ P T следует [Birch, 1952]

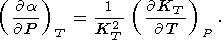(30)

Это фундаментальное соотношение записывается в безразмерной форме

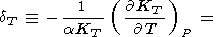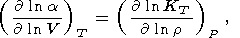(31)

где вводится изотермический параметр Андерсона-Грюнайзена [O. Anderson, 1966a, 1967; Barron, 1979].

Изменение a c температурой при P = const характеризуется безразмерным параметром a [Furth, 1944; O. Anderson, 1966b; Birch, 1986; O. Anderson et al., 1993]

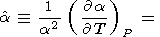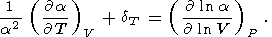(32)

Член

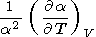можно связать с производными C_V и K_T, используя тождество ²S/ V T = ² S/ T V, что приводит к

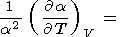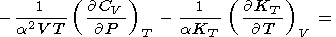(33)

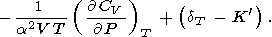Аналогично тождество ² S P T = ² S T P дает

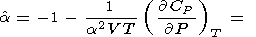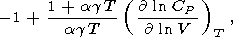(34)

где введено удобное безразмерное произведение

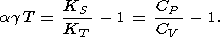Берч [Birch, 1952] указал, что параметр d_T для различных веществ обычно лежит в интервале между 4 и 8 (при P = 0 и T = 300 K), что и было подтверждено в дальнейшем [см. Sumino and O. Anderson, 1984; O. Anderson et al., 1990, 1992a; Boehler, 1992]; встречаются, однако, исключения: например, минералы KMnF ₃ ( d_T 1 ) и Re ₂ O ₃ ( d_T 77 ).

Параметр a при нормальных условиях обычно существенно превышает d_T [Birch, 1952; O. Anderson et al., 1992a]. Данные и оценки, собранные в таблицах [Паньков и др., 1997] для 25 мантийных минералов, дают область 10 a 270. Однако при высокой температуре ( T > Q ) d_T и a cущественно сближаются, а их совпадение означало бы, что a зависит лишь от объема (т.е. собственный ангармонизм в (32) подавляется).

Представляют интерес следующие три допущения и их следствия.

(1) Теплоемкость C_V не зависит от давления, т. е. C_V = C_V(T) (как в уравнении Ван-дер-Ваальса или Хильдебранда [O. Anderson, 1979]), или C_V = const (как в классическом пределе при T > Q ). Тогда из (33) и (32)

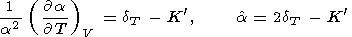(35)

Обычно, при P = 0, d_T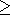 K.

(2) K_T зависит лишь от объема, т.е. K_T(V) - приближение, часто оправдывающееся при T > Q [O. Anderson, 1982; D. Anderson, 1988, 1989]. Тогда ( K_T/ T)_V = 0 и из (29) и (31) имеем K = d_T, т.е. d_T зависит лишь от объема или является константой (последний случай ведет к уравнению Мурнагана (44)).

(3) Если одновременно выполняются указанные выше условия (1) и (2), то имеем a = a(V) и K = d_T = a (зависит лишь от объема или константа).

6.2. Явная зависимость a от объема или давления при T = const

В большей части земных недр T > Q и a слабо зависит от температуры. Рассмотрим ряд приближенных формул для оценки изотермического или адиабатического изменения a.

6.2.1.

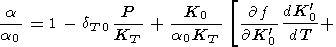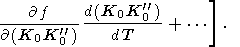(36)

Если в (36) сохранить лишь два первых члена, то получится формула Берча [Birch, 1952, 1968]. Заметим, что тогда a меняет знак при K_T/P = d_T0 - условие, которое может достигаться в нижней мантии ( K_T/P = 4.7 ). Более того, в этом случае для большинства уравнений состояния типа (28) d_T вместо обычного убывания (см. раздел 9) растет с давлением. Однако обращение знака a с ростом давления невозможно с точки зрения термодинамики [Паньков, 1992].

В качестве примера использования (36) мы вычислили a(P/K₀) c помощью уравнения состояния из работ [Ullmann and Pankov, 1976, 1980], в котором

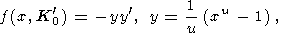	(37)

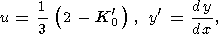так что

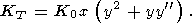(38)

Вначале мы полагаем dK₀/ T = 0 и пренебрегаем членами, содержащими K₀, K₀,.... Кривые a/a₀ в зависимости от P/K₀, полученные отсюда при характерных значениях K₀= 3 и 4 и d_T0 = 2,4 и 6, показаны на рис. 1. Зависимость P/K₀ от x изображена на рис. 2. Мы видим, в частности, что в условиях нижней мантии влияние d_TO на оценку a очень существенно (у основания мантия при сжатии вдоль ее "горячей" адиабаты x 0.7 и P/K₀ 0.70 для K₀ 1.9-2.0 Mбар и K₀ = 3.8-4.1 [D. Anderson, 1989]). Кроме того, использованное приближение для a может приводить к некорректному результату a< 0 в пределах нижней мантии.

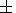Для иллюстрации влияния dK₀/ T мы используем теперь третье слагаемое в (36), полагая dK₀/ T = 2 10^-3 K^-1 - значение, вытекающее из наших оценок для NaCl по данным, которые обсуждал Берч [Birch, 1978]. Значение 2 10^-3 К^-1 нереалистично, так как приводит к росту a с давлением (рис.1 и 3). С другой стороны, отрицательное значение - 2 10^-3 этой производной слишком мало, так как при этом значительно уменьшается давление, при котором достигается условие a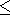 0.

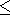Приближения K = d_T (см. выше) и d_T const при T > Q указывают на очень слабую зависимость K от температуры. Модели решеточной динамики [Hemley et al., 1989] показывают, что K для перовскитовой фазы MgSiO ₃ изменяется меньше, чем на 10% в области температур 300-2000 К ( dK₀/ T 2 10^-4 \ K^-1 ). Теоретическая модель PIB для MgO [Isaak et al., 1990; O. Anderson et al., 1993] дает некоторое увеличение dK₀/ T с температурой в том же интервале 300-2000 К со средними значениями, изменяющимися от 2.8 10^-4 до 4.2 10^-4 К ^-1. Величины того же порядка следуют из соотношения d ln K₀/d ln r = -1, указанного в [D. Anderson, 1989] для модели PREM.

Производную dK₀/dT можно оценить также из упомянутого выше допущения K_T = K_T(V) (т.е. K = d_T и учитывается (70)):

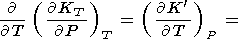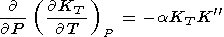(39)

(штрихи означают производные по давлению). Положив a 3 10^-5 К ^-1 и - K_TK 5-10 [напр., Pankov and Ullmann, 1979; Hofmeister, 1991], найдем dK₀/ T (1-3) 10^-4 K ^-1, что близко к приведенным выше оценкам.

Наконец, забегая вперед, воспользуемся тождеством (91), которое, конечно, приводит к (39) при K = d_T (см. (71)). Хотя члены в (91) близки друг к другу, из соображений, приведенных ниже, следует, что (d_T/ P)_T 0 и, следовательно,

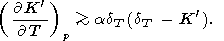(40)

Подставляя сюда данные для параметров справа (таблицы 2, 3 и [Паньков и др., 1997]), находим

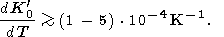Подчеркнем, что поправка к a по (36), связанная с этой производной, позволяет избежать как отрицательных a при высоких давлениях, так и роста a c давлением. На рис. 1 показано влияние параметра dK₀/dT = 2 10^-4 K ^-1 на кривую a c параметрами K = d_T0 = 4.

6.2.2.

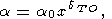(41)

интегрируя (30) и используя (8) при условии

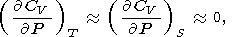которое дает

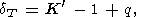(42)

где введено обозначение

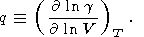(43)

Кроме того, он допустил d_T K const. Постоянство K (или условие K = K(T) ) приводит к уравнению Мурнагана (типа (28))

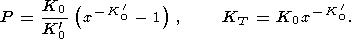(44)

Ясно, что (41) просто следует из определения d_T по (31) при условии, что d_T либо зависит только от T, d_T = d_T (T), либо является константой, а вместо (44) можно использовать любую подходящую аппроксимацию изотермы P(V, T₀).

Однако две функции a (V, T) и P (V, T) нельзя выбирать независимо. В частности, задание a (V, T) и P (V, T₀), очевидно, определяет уравнение состояния P (V, T). В этой связи полезно следующее обобщение выводов ряда авторов [Clark, 1969; Birch, 1966; O. Anderson, 1986; D. Anderson, 1989]. Рассмотрим четыре утверждения: (1) справедливо (44), где K₀ - функция температуры, K₀ (T), а K₀ либо константа, либо зависит от T; (2) (d_T/ P)_T = 0 (т.е. d_T = const или d_T = d_T (T) ); (3) ( K/ T) P = 0 ; (4) d_T = K, что, согласно (71), равносильно K_T = K_T (V) (т.е. t (T) = aK_T или t = сonst).

Тогда с помощью тождеств (44), (71), (91) и (92) можно доказать, что, если два из этих утверждений (кроме пары (1) и (3)) одновременно выполняются, то и другие два справедливы; более того, тогда d_T = K = const и, соответственно, имеет место (44). Если же дополнительно (к двум утверждениям) C_V = сonst или C_V = C_V(T), то a = a(V), K = d_T = a = const и t = const (см. раздел 6.1 и (69), (71)).

Понятно, что такие утверждения накладывают ограничения на уравнения состояния. Если используется, например, уравнение типа (28) вместо уравнения Мурнагана, то только одно из приведенных выше утверждений может строго соблюдаться. В частности, одновременное использование уравнения Берча-Мурнагана и допущения d_T = d_T(T) или d_T = const несовместимо ни с условием d_T = K, ни с условием K = K(P).

Другой не очевидный вывод состоит в том, что уравнение Мурнагана (44) однозначно выводится из предположений K_T = f(P) + aT (a = const) и t = t (T) или const.

Интересное замечание касается использования мурнагановской формулы для описания потенциальной (или решеточной) части уравнения состояния в классическом высокотемпературном приближении. В общем случае при C_V = const имеем линейную зависимость K_T (V, T) от T (cм. (69) и (70)), и лишь при g/x = const (q = 1) и мурнагановском потенциале мы получаем

где a, b и c - постоянные ( K = const ). Отсюда видно, что все изотермы ( T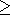 0 ) также описываются формулой (44), но при нелинейных зависимостях g(x) это уже не так.

Приведенное выше рассмотрение имеет отношение и к закону Берча, который для минералов со средним атомным весом m = 20-22 г/моль можно записать в универсальной степенной форме K_T = aV^b (где a и b - константы, а раличием между K_S и K_T пренебрегается). Так как здесь K = const, K_T = K_T(V) и используется (44), этот закон приводит к d_T = K = const, формуле (41) и, при C_V = const, к a = a (V).

Чтобы проиллюстрировать поведение a по (41) в плоскости a/a₀-P/K₀, мы использовали уравнение состояния (37) с K₀ = 3 и 4 (соответствующие кривые a проходят через концы вертикальных черточек на рис. 1.

Первоначальное предположение О. Андерсона [1967] d_T = const оправдывалось имевшимися в то время ультразвуковыми и ударноволновыми данными и, казалось, подтверждается более поздними спектроскопическими, ультразвуковыми и резонансными измерениями [O. Anderson et al., 1990; Chopelas and Boehler, 1992]. В частности, по данным для семи минералов значение d_T = 4-6 было рекомендовано как представительное для материала нижней мантии. Однако D. Anderson, [1987, 1989] по данным сейсмологии и геоида нашел для нижней мантии значение in situ d_T = 2-3. Следовательно, возникает предположение, что d_T должно убывать с давлением. Основания для этого можно найти в ударноволновых и статических данных [Birch, 1986; O. Anderson et al., 1993].

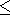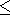Теоретические ab initio расчеты [Reynard and Price, 1990] для MgO дают постоянное d_T в интервале 0.7 x 1.0. Другие ab initio результаты [Isaak et al., 1990] показывают, однако, что d_T убывает с уменьшением x.

Шопла и Белер [Chopelas and Boehler, 1992] использовали данные по адиабатическому градиенту t_S и теплоемкости C_P для определения более точной зависимости a(x), чем степенной закон (41). Из соотношения Максвелла (14) они нашли

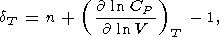(45)

где n ( lnt_S/ ln V)_T. Далее они положили n = mx, где m = 6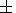 1 по измерениям для плохо сжимаемых веществ, и ( ln C_P/ ln V)_T = 1 или 0 при T < Q или T > Q, соответственно (ср. с данными в таблице 3 и [Паньков и др., 1997]). Таким образом, их формулу для a можно записать в виде

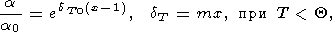(46)

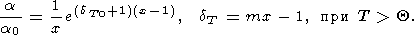(47)

В работах [O. Anderson et al., 1992а, 1992b, 1993] был предпочтен степенной закон d_T = d_T0 x^k (при T Q ), который дает

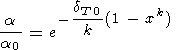(48)

c небольшими отклонениями от (47). Значение k = 1.1-1.4 было выведено из теоретической модели PIB для MgO [Isaak et al., 1990].

Для нижней мантии формулы (47) и (48) показывают, что начиная от состояния P = 0, T 1700-2000 K (адиабатически разгруженная нижняя мантия), a вдоль "горячей" мантийной адиабаты убывает в 4-5 раз при достижении подошвы мантии. Степенной закон (41) с d_T = 5-6 дает более сильное убывание (6-8 раз), а с d_T = 2-3 - более слабое (2-3 раза). Хотя формулы (47) и (48) предпочтительнее, чем (41), они требуют дальнейшего подтверждения и информации о параметрах m, k и ( ln C_P/ ln V)_T. Для сравнения отметим, что изложенный в пункте 6.2.1 метод оценки a по (36), (37) дает для нижней мантии результаты, близкие к a по (47) или (48) при использовании в (36) значения dK₀/dT = 2.3 10^-4 K ^-1 (рис. 3).

Качественно подобные результаты для a c убывающим при сжатии d_T были получены Жарковым [1997] из анализа уравнений состояния при сверхвысоких давлениях. Еще раньше [Жарков, 1959] он показал, что термодинамика нижней мантии, основанная на дебаевской модели, дает 4-5-кратное убывание a у основания мантии по сравнению со значением при P = 0.

6.2.3.

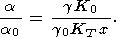(49)

Термодинамический параметр g, вообще говоря, отличается от так называемого решеточного параметра Грюнайзена [напр., Mulargia, 1977, 1979; D. Anderson, 1989; O. Anderson, 1968, 1979, 1980]. Oднако, если допускается, что последний зависит лишь от объема, то оба параметра совпадают (к этому же приводит и квазигармоническая модель уравнения состояния при высокой температуре, когда, с другой стороны, имеем чисто термодинамическое следствие g = g (V) при C_V = const (cм. раздел 11).

Три наиболее известные формулы для решеточного g можно записать в общем виде [Жарков, Калинин, 1968; Irvine and Stacey, 1975]

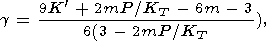(50)

где m = 0, 1, 2 дает, соответственно, формулы Слейтера, Дугдайла-Макдональда и Зубарева-Ващенко. Последняя представляется наиболее предпочтительной, по крайней мере при T > Q для высокосимметричных кристаллов. Согласно Лейбфриду и Людвигу [Leibfried and Ludwig, 1961], g можно приближенно найти по среднеквадратичной частоте атомных колебаний. В случае кубических кристаллов с центральным взаимодействием и учетом лишь ближайших соседей это также приводит к формуле Зубарева-Ващенко [Pankov, 1983; Hofmeister, 1991].

Применение (50) требует знания зависимости P (V) на нулевой изотерме, хотя g по (50) нечувствительно к замене изотермы T = 0 K на какую-либо изотерму T > 0 К. Если воспользоваться уравнением состояния (37) с K₀ = 4 и затем найти g по (50) при m = 2 и a/a₀ по (49), то при x = 0.7 (примерно у подошвы мантии) получим a₀/a = 1.7. Столь небольшое уменьшение a по сравнению с найденным выше убыванием в 4-5 раз связано с тем, что уравнение состояния (37), как и многие другие зависимости P (V) [Pankov and Ullmann, 1979b], дает по (50) очень низкое значение наклона

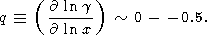Это либо указывает на необходимость введения более гибкого уравнения состояния с независимым параметром K₀K₀ K₂ (такого, как, например, модель 2 в [Ullmann and Pankov, 1980] или уравнение Берча-Мурнагана четвертого порядка), либо требует поправок к формуле для g. Формула (50) с m = 2 была усовершенствована в работе [Stacey, 1981], но при этом наклон q для уравнения состояния с ограниченным числом параметров, по-видимому, остается низким.

Другим важным приближением для g является эмпирический степенной закон [напр., O. Anderson, 1968; McQueen, 1970; Jeanloz and Ahrens, 1980a, 1980b]

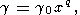(51)

где q часто допускается равным 1, согласно ударноволновым данным [McQueen, 1992] или исследованиям мантии [O. Anderson, 1979b; D. Anderson, 1989]. При q = 1 из (49) следует формула Берча aK_T = a₀ K₀ = const, которая дает в подошве мантии a₀/a = 3.5-4.0 (при x = 0.7, K₀ = 4, K_T/K₀ = 3.51 и T = 2000-3000 K). Значение q = 1.5-2.0, более предпочтительное для мантийного перовскита [Паньков и др., 1997], приводит, однако, к a₀/a = 4.2-5.0, что близко к результату по (47) и (48).

Заметим, что, согласно (49), степенные законы для a (41) и g (51) снова возвращают нас к уравнению Мурнагана (44). Так как последнее обычно удовлетворительно описывает данные при P/K₀ 0.3 (x 0.82), можно ожидать, что (41) будет достаточным приближением для a в той же области сжатий.

Даффи и Аренс [Duffy and Ahrens, 1993] вычислили a по ударноволновым данным для MgO, CaO, CaMgSi ₂ О ₆ и e -Fe до давлений P > 140 GPa. Используя (49) и (51) с q = const, а также K_T/K₀ из модели PIB для MgO [Isaak et al., 1990], они нашли q = 0.5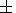 0.5, что меньше, чем q = 0.83-1.26 в области сжатий x = 0.67-1.0 на изотерме PIB [Isaak et al., 1990]. Периклаз более сжимаем, чем вещество нижней мантии, так что для него x = 0.67 при P = 134 GPa вблизи подошвы мантии (согласно изотерме PIB при 2000 К, имеем P/K₀ = 1.047, K_T/K₀ = 4.699, K = 4.74 ). C этими значениями результаты Даффи и Аренса дают для MgO у основания мантии (при x = 0.67) a₀/ a = 3.1-4.7, что в 1-1.6 раз меньше, чем a₀/a из (47), (48) с характерным значением d_TO = 5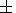 1 (значение d_TO = 4 приближает оценку a₀/a по (47), (48) к ударноволновому результату). Эти данные можно также рассматривать как аргумент в пользу убывания как d_T, так и q при сжатии.

В одном из последних анализов зависимости g от объема [O. Anderson et al., 1993] был принят степенной закон

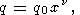(52)

который аналогично (48) дает

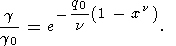(53)

Полагая q₀ = 1.5-2.0 и n = 1 (MgO по [O. Anderson et al., 1992b]), из (49) найдем a₀/a = 4-4.5 при x = 0.7. Отметим, что q₀ для MgO, согласно [O. Anderson et al., 1993], убывает от 1.72 до 1.26 с ростом температуры от 300 К до 2000 К.

В целом, многочисленные оценки a₀/a разными методами, описанными выше, согласованно показывают, что коэффициент теплового расширения убывает в 4-5 раз вдоль "горячей" адиабаты нижней мантии при изменении давления от 0 до основания мантии. Однако полного согласия по всем параметрам, связанным с этими оценками (например, по q и d_T ) пока нет.

6.3. Зависимость a от температуры при P = 0

6.3.1.

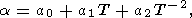(54)

которая использовалась нами для вычисления a при высокой температуре (таблица 2 и [Паньков и др., 1997]). Ее применимость оправдывается также расчетами фазовых диаграмм [Fei et al., 1990, 1991].

Более корректным, по-видимому, является метод Сузуки [Suzuki, 1975], в котором a определяется из уравнения Ми-Грюнайзена

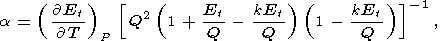(55)

где E_t - дебаевская тепловая энергия

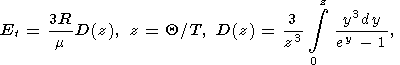k = 12(K₀ - 1), Q = K₀ V₀g и D (z) - функция Дебая. Здесь g = const и параметры K₀ и K₀ в данном случае определяются при T = 0. Подгоночными параметрами являются Q, k и Q. Формула (55) следует из разложения потенциального давления по V, в котором учитываются лишь первые два члена. Значения Q, полученные этим методом, приведены в таблице 2 и работе [Паньков и др., 1997].

O. Anderson et al. [1992] экстраполировал a₀ (T) от фиксированного значения при T > Q к высоким температурам с помощью соотношения

(56)

где d_T = a = const (см. (32)). Формулу (56) легко вывести из условия, что a₀ при P = 0 изменяется с плотностью по степенному закону. Заметим, что (56) имеет асимптоту, вблизи которой a резко возрастает с T, что в какой-то степени отражает тот факт, что потенциальная энергия при растяжении кристалла проходит через точку перегиба.

6.3.2.

This document was generated by TeXWeb (Win32, v.1.0) on August 10, 1998.