3. Уравнения состояния и калорические функции

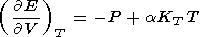
Фундаментальное уравнение (1) связывает пять переменных, две из которых являются независимыми. Следовательно, полное описание термодинамической системы получается, если известны ее термическое P(V,T) и калорическое E(V,T) уравнения состояния. Термическое уравнение состояния, поскольку оно связывает экспериментальные P-T и теоретические V-T переменные, необходимо для преобразования этих переменных при анализе любой физической характеристики [Жарков, Калинин, 1968]. Параметры, определяемые из этого уравнения, называются термическими характеристиками системы, а величины, для определения которых требуется либо только калорическое, либо оба типа уравнений состояния, называются калорическими. К последним относятся, в частности, K_S, g, C_P, t_S.

Два типа уравнений состояния связаны соотношением

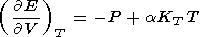(21)

или

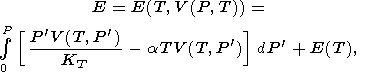где использовано преобразование

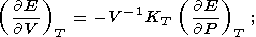постоянная интегрирования равна

и интеграл берется вдоль изотермы. Вследствие указанной связи, для определения E(V,T) достаточно знать термическое уравнение состояния и E(T) или энтальпию H(T) при P = 0. Для тех же целей можно использовать любую из калорических функций H(T), S(T), G(T), C_P(T) при P = 0, так как имеют место следующие тождества

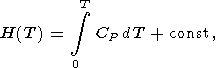(22)

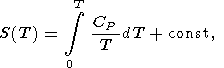(23)

Последняя формула записывается также в виде

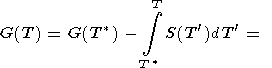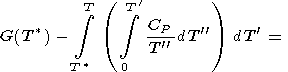(24)

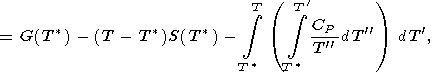где T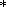 - некоторая фиксированная температура, выбранная из соображений удобства.

Для минерала, состав которого представляется суммой окислов (компонент), энергия Гиббса выражается через разностные члены

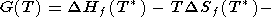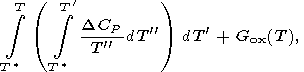(25)

где

DH_f = H - H _ox, DS_f = S - S _ox, DC_P = C_P - C_{P ox} - соответственно, энтальпия и энтропия образования минерала из окислов и разность теплоемкостей минерала и окислов (с учетом стехиометрических коэффициентов). Выражения типа (25) часто применяются в расчетах фазовых равновесий [Navrotsky and Akaogi, 1984; Kuskov and Galimzyanov, 1986; Fabrichnaya and Kuskov, 1991; Fei and Saxena, 1986; Fei et al., 1990; Sobolev and Babeyko, 1989]. При этом некоторые авторы используют приближение DC_P = 0 (или const 0, или DC_P (T) из эмпирических выражений типа (67)). В любом случае член DH_f (T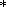) в (25) неявно содержит произвольную нормировочную константу [Калинин и др., 1991].

Из (3) следует

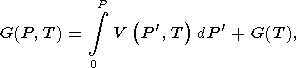(26)

где G (T) = G (T, 0) определяется по (24) или (25), причем последняя из этих формул может быть записана в сокращенной форме

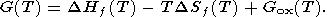(27)

Методы определения уравнений состояния в геофизике можно классифицировать следующим образом.

(1) Макроскопический подход, основанный Мурнаганом [Murnaghan, 1951] и Берчем [Birch, 1952]. Он дает зависимость давления от объема при T (или S ) = const типа [Ullmann and Pankov, 1976]

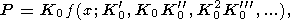(28)

где (и далее, если не оговорено) величины с индексом 0 относятся к P = 0 и произвольной температуре, x = V/V₀ = r₀/r и модули K₀ K_T0, K₀ = ( K_T/ P)_T0, ... - материальные параметры. Большинство данных по этим параметрам получено при комнатной температуре [напр., Sumino and O. Anderson, 1984]. Среди последних достижений экспериментальных исследований следует отметить ультразвуковые измерения при высоких давлениях [Fujisawa, 1987; Webb, 1989; Yoneda, 1990; Liebermann et al., 1993], рентгеновские данные при высоких давлениях и температурах [напр., Yagi et al., 1987; Plymate, 1990; Mao et al., 1991; Fei et al., 1992a, 1992b; Boehler et al., 1989], наблюдения колебательных спектров [напр., Chopelas, 1990a, 1990b, 1991a, 1991b, 1993; Hoffmeister, 1987, 1991] и высокотемпературные измерения упругих модулей при P = 0 резонансным методом [O. Anderson et al., 1992a; O. Anderson, 1995].

Явный вид функции f (зависимости от объема) рассматривался Мурнаганом [Murnaghan, 1951], Берчем [Birch, 1952, 1968, 1978, 1986] и многими другими [Thomsen, 1970, 1971; Ahrens and Thomsen, 1972; Davies, 1973; Ullmann and Pankov, 1976, 1980; Pankov and Ullmann, 1979; Stacеy, 1981; Aidun et al., 1984; Jeanloz, 1989; Bina and Helffrich, 1992; Isaak et al., 1992; Wall et al., 1993]. Наиболее популярным соотношением данного типа является уравнение Берча-Мурнагана.

Упругие модули и скорости звука в минералах зависят прежде всего от состава, кристаллической структуры, давления и температуры. Данные по этим зависимостям были обобщены в виде ряда эмпирических закономерностей, названных законом Берча, сейсмическим уравнением состояния, законом соответственных состояний, универсальными уравнениями состояния [Birch, 1966; O. Anderson and Nafe, 1965; D. Anderson, 1967, 1987; Chung, 1973; Davies, 1976; O. Anderson, 1973; D. Anderson and O. Anderson, 1970; Mao, 1974; Калинин, 1972; Schankland and Chung, 1974; Campbell and Heinz, 1992]. Эти закономерности позволяют оценивать параметры K₀ и с меньшей точностью K₀ [D. Anderson, 1988; Duffy and D. Anderson, 1989].

(2) Статистическая физика твердых тел, описывающая колебания атомов в кристаллах, приводит к микроскопической теории уравнений состояния, включающей фундаментальное уравнение Ми-Грюнайзена [Gruneisen, 1926; Born and Huang, 1954; Leibfried and Ludwig, 1961; Knopoff, 1963; Knopoff and Shapiro, 1969; Жарков, Калинин, 1968; Wallace, 1972; Mulargia, 1977; Mulargia and Boschi, 1980; Hardi, 1980; O. Anderson, 1980; Gillet et al., 1989, 1990, 1991; Richet et al., 1992; Reinard et al., 1992]. В этом подходе также используются различные полуэмпирические потенциалы атомных сил или выражения для опорных P - V зависимостей и решеточные или колебательные параметры Грюнайзена [напр., Альтшулер, 1965; Жарков, Калинин, 1968; Ahrens and Thomsen, 1972; McQueen, 1991]. Материальные параметры при этом определяются по данным статического и динамического сжатия, упругих модулей, теплового расширения, калорических функций и колебательных спектров.

(3) Интегрирование соотношения (12) (см. раздел 8.2) дает давление в виде суммы двух членов: опорной изотермы и приращения теплового давления DP_th. Этот термодинамический подход, основанный на экспериментальных данных, был развит О. Андерсоном [O. Anderson, 1979a, 1979b, 1979c, 1980, 1982, 1984, 1988, 1995], который уделил особое внимание анализу теплового давления. Он широко использовался для описания рентгеновских и резонансных данных [O. Anderson et al., 1982, 1992a; O. Anderson and Yamamoto, 1987; O. Anderson and Zou, 1989; Mao et al., 1991; Fei et al., 1992a, 1992b].

(4) Более сложные теоретические модели уравнений состояния выводятся путем расчетов с использованием методов Хартри-Фока, Томаса-Ферми, псевдопотенциалов, полуэмпирических потенциалов, молекулярной динамики [Hemley et al., 1985, 1987; Isaak et al., 1990; Wolf and Bukowinski, 1987, 1988; Wall and Price, 1988; Wall et al., 1986; D'Arco et al., 1991; Price et al., 1989; Matsui et al., 1987, 1991; Matsui, 1988, 1989; Reynard and Price, 1990; Agnon and Bukowinski, 1990; Walzer, 1992; Cohen, 1987; Dovesi et al., 1987; Catlow and Price, 1990; Boisen and Gibbs, 1993; Silvi et al., 1993; Catti et al., 1993; Barton and Stacey, 1985].

Как упоминалось выше, простая система полностью описывается термодинамически, если для нее известен какой-либо из термодинамических потенциалов или известны термическое уравнение состояния и одна из калорических функций. В таблице 1 суммированы различные подходы, показывающие, какие функции должны быть найдены экспериментально или теоретически, чтобы обеспечить такое описание. Эти подходы можно также сформулировать в виде уравнений в частных производных с соответствующими граничными условиями.

4. Термодинамические параметры третьего и дальнейшего порядков

Порядок термодинамической характеристики определяется максимальным порядком производной термодинамического потенциала, входящей в ее определение. Чтобы найти все параметры третьего порядка ( P - V - T - S производные параметров второго порядка), полное число которых для потенциалов (1)-(4) равно 16, достаточно задать, кроме параметров низшего порядка, четыре независимых и соответственно выбранных параметра третьего порядка. В частности, из эксперимента мы часто имеем информацию о производных ( K_S/ P)_T (или

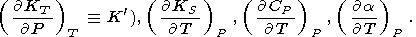Соотношения, связывающие их с остальными параметрами, приводятся ниже в соответствующих разделах.

Для экстраполяции данных по термодинамическим свойствам к высоким давлениям и температурам часто используется степенная зависимость от объема, согласно которой логарифмическая производная по этой переменной полагается равной константе [Жарков, 1968; D. Anderson, 1988, 1989]. При этом производная по температуре какого-либо параметра A при P = const представляется в безразмерном виде

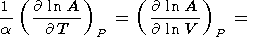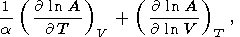(29)

где первое слагаемое характеризует так называемую собственную ангармоничность, а второе - внешнюю ангармоничность, связанную с тепловым расширением [Jones, 1976; Smith and Cain, 1980]. Параметром A может служить любая физическая характеристика, например, коэффициенты транспортных процессов или модовые параметры Грюнайзена [Reynard et al., 1992; Gillet et al., 1989].

5. Термодинамическая база данных

База данных по свойствам минералов, необходимым для геофизического анализа и построения уравнений состояния, должна включать прежде всего плотность и параметры второго и третьего порядков. Пример подобной базы данных для трех минералов приведен в таблицах 2 и 3, а база данных для 25 мантийных минералов, включая их фазы высокого давления (в том числе фиктивные фазы), представлена в системе Internet [Паньков и др., 1989]. Данные в этих таблицах относятся к условиям P = 0, T = 300 K и P = 0 и указанной вверху температуре. Таблица 2, кроме параметров второго порядка, включает молярную массу M, средний атомный вес m, плотность r, температуру плавления T_m, дебаевские температуры Q ( Q_a - акустическая температура Дебая, Q_a из подгонки уравнения Ми-Грюнайзена к данным по a [Suzuki, 1975], Q_th - наша оценка по теплоемкости), классическое значение C_V = 3R/m ( R - газовая постоянная), энтальпию DH_f и энтропию DS_f образования минерала из окислов и оценку теплового давления P_th 0.5aK_T. Важно иметь самосогласованные значения параметров второго порядка: здесь в качестве входных параметров мы использовали экспериментальные значения K_S (или K_T ), a и C_P. При высокой температуре T > 300 K величины a и C_P определялись по эмпирическим формулам из работ [Fei and Saxena, 1987; Fei et al., 1990, 1991], а для K_S приведены либо экспериментальные значения, либо оценки через параметр Андерсона-Грюнайзена d_S (300 K), который допускался постоянным (см. таблицу 3 и разделы 9, 10). Для величин, приведенных в таблице 3, входными параметрами служили призводные ( K_S/ P)_T, ( K_S / T)_P (или d_S ), ( C_P/ T)_P, a = a^-2(a/ T)_P и указанные в таблице 2 плотность и параметры второго порядка. Высокотемпературные значения этих производных оценивались при условии ( K_S/ P)_T const. Наконец, в таблице 2 для каждого минерала собраны ссылки на источники экспериментальных данных по их термодинамическим свойствам.

This document was generated by TeXWeb (Win32, v.1.0) on August 10, 1998.