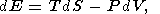
С термодинамической точки зрения, Земля является тепловой машиной, характеризуемой множеством параметров, которые определяются из уравнений состояния и моделей кондепарованных сред. В разработке этих моделей достигнут большой прогресс [напр., Jeanloz, 1983; Hemley et al., 1985, 1987; Wall et al., 1986; Catti, 1986; Cohen, 1987; Dovesi et al., 1987; Wolf and Bukowinsky, 1987, 1988; Wall and Price, 1988; Matsui et al., 1987; Matsui, 1988, 1989; Price et al., 1989; Catlow and Price, 1990; Isaak et al., 1990; Reynard and Price, 1990; Agnon and Bukowinsky, 1990a; Matsui and Price, 1991; D'Arco et al., 1991; Walzer, 1992; Silvi et al., 1993; Catti et al., 1993; Boison and Gibbs, 1993]. Однако практические исследования в геофизике в большой степени основаны на использовании полуэмпирических уравнений состояния [Birch, 1952, 1986; O. Anderson, 1966b, 1995; Pankov and Ullmann, 1979; D. Anderson, 1967, 1987, 1989; Stacey, 1981; Bina and Helffrich, 1992; Wall et al., 1993]. Прямое определение свойств геоматериалов на основе экспериментальных данных при высоких давлениях и температурах необходимо для решения многих задач геофизики и дает важные ограничения на структуру уравнений состояния.
Со времени фундаментальной работы Берча [Birch, 1952] была накоплена огромная информация по свойствам геоматериалов и их геофизическим приложениям [напр., Stacey, 1977a, 1977b; Jeanloz and Thompson, 1983; Brown and Shankland, 1981; Жарков и Калинин, 1968; Zharkov, 1986; Jeanloz and Knittle, 1989; O. Anderson et al., 1992a, 1992b, 1993; Kuskov and Panferov, 1991; D. Anderson, 1989; O. Anderson, 1988, 1995]. Настоящая работа посвящена обзору и анализу связей между основными термодинамическими характеристиками геоматериалов и их изменения с давлением и температурой. Прежде всего мы имеем дело с восемью параметрами 2-го порядка. Внимание обращается на их самосогласованное определение, связь с уравнениями состояния, сводку подходов к определению уравнений состояния. Приводится пример самосогласованной базы данных по термодинамическим свойствам минералов. Далее каждый из параметров 2-го порядка рассматривается отдельно: устанавливаются тождественные соотношения между их P-T производными (параметрами 3-го порядка) и анализируются практически полезные приближенные соотношения, включая примеры явных P-T зависимостей параметров 2-го порядка. Приводятся оценки некоторых параметров 4-го порядка. Соотношения между различными параметрами представляются в виде, удобном для практического использования экспериментальных данных и теоретического анализа. Наконец, даны некоторые приложения результатов к оценкам свойств нижней мантии. Наш анализ служит дополнением к обзорам, представленным в работах [O. Anderson, 1995; Stacey, 1995].
В классической термодинамике простые системы, испытывающие обратимые изменения состояния, описываются множеством параметров, включая гидростатическое давление P, температуру T, объм V или плотность r и энтропию S. Отправным пунктом термодинамического анализа являются стандартные выражения для полных дифференциалов термодинамических потенциалов [напр., Callen, 1960; Morse, 1969; Kelly, 1973]
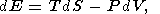 | (1) |
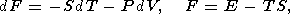 | (2) |
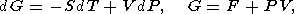 | (3) |
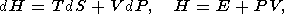 | (4) |
где E - внутренняя энергия, F - свободная энергия, G - энергия Гиббса и H - энтальпия.
Для описания термодинамических свойств в геофизике используются восемь параметров второго порядка: коэффициент объемного теплового расширения a, изобарическая CP и изохорическая CV теплоемкости, изотермический KT и адиабатический KS модули сжатия, термический коэффициент давления t и адиабатический градиент температуры tS. Эти параметры определяются формулами
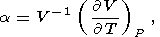 | (5) |
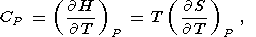 | (6) |
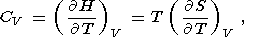 |
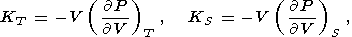 | (7) |
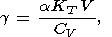 | (8) |
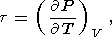 | (9) |
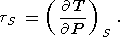 | (10) |
Используя равенство вторых смешанных производных термодинамических потенциалов, из (1)-(4) получаем четыре соотношения Максвелла [см. также Stacеy, 1977a]
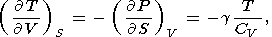 | (11) |
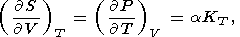 | (12) |
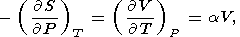 | (13) |
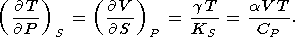 | (14) |
Легко показать, что вторые производные термодинамических потенциалов выражаются через введенные выше параметры или характеристики
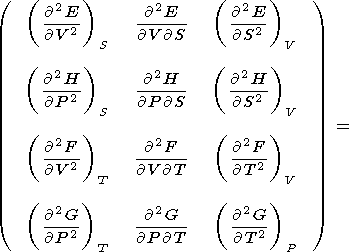 |
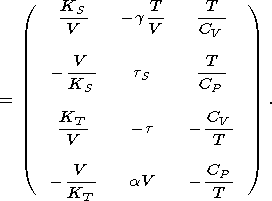 | (15) |
Ясно, что число независимых параметров второго порядка равно трем, и, следовательно, восемь введенных параметров связаны между собой пятью соотношениями. Четыре из них - это (11)-(14), а пятое можно получить, переходя от одной пары характеристических переменных к другой; в частности,
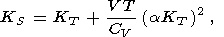 | (16) |
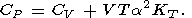 | (17) |
Таким образом, если из эксперимента известны, как обычно, a, CP, KS (или KT ), то пять упомянутых выше соотношений можно записать в виде
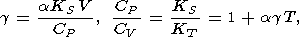 |
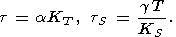 | (18) |
Приведем два примера использования термодинамических соотношений в геофизике. Первый из них касается уравнения Вильямсона-Адамса для градиента плотности внутри Земли [Birch, 1952; D. Anderson, 1989], которое мы представим здесь в виде
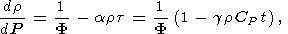 | (19) |
где r и P плотность и давление в Земле, F = KS/r - сейсмический параметр, t = dT/dP - tS - сверхадиабатический градиент температуры в Земле. Уравнение (19) легко получается из
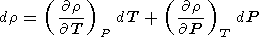 |
с помощью (5), (16) и (14) или (18).
Другой пример - адиабатический градиент температуры по глубине l в Земле (см. (14))
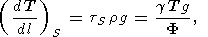 | (20) |
где g - ускорение силы тяжести и использовано уравнение равновесия dP/dl = rg. Согласно модели Земли PREM [D. Anderson and Dziewonski, 1981\link], F = 50, 80 и 117 км 2 /c 2 на глубинах, соответственно, 400, 1071 и 2740 км. Полагая T = 1700 K, 2200 К и 3000 К последовательно на тех же глубинах [D. Anderson, 1989; Паньков, 1989] и g = 1-1.5, получаем (dT/dl)S = 0.3-0.5 K/км - величина, обычно цитируемая в геофизической литературе.