
В. П. Трубицын, В. В. Рыков
Институт физики Земли им. О. Ю. Шмидта, Российская академия наук, Москва
 80. В
мантии устанавливается развитая нестационарная тепловая конвекция
с узкими нисходящими и восходящими потоками в виде плюмов со
скоростями мантийных течений от 1 до 10 см/год. Далее в некоторый
момент в мантию помещается континент в виде тонкой длинной
пластины толщиной
d =0.03 и длиной
l =2.0 от толщины всей мантии, что
в размерном виде соответственно составляет
d =90 км и l=6 тыс км.
Чтобы продемонстрировать эффект прогревания мантии под
континентом, он помещается на самое холодное место мантии, где в
данный момент оказалось больше нисходящих мантийных потоков.
Эволюция системы мантия-континент находится численным решением
уравнений переноса импульса, массы и тепла для вязкой жидкости и
твердого континента. Дается строгая формулировка задачи, приводится
самосогласованный метод решения полной системы связанных
интегродифференциальных уравнений и указывается метод их
численной реализации. Сначала в течение долгого времени (порядка
500 Ma) континент практически остается неподвижным, но в мантии
происходит кардинальная перестройка течений, в результате которой
холодные нисходящие мантийные потоки под континентом
подавляются, а вместо них под континент стягиваются горячие
восходящие потоки. После этого под влиянием результирующей силы
вязкого сцепления с мантийными течениями континент начинает
перемещаться с переменной скоростью в среднем порядка 1 см/год.
При этом в результате механического сцепления и теплового
взаимодействия с движущимся континентом структура мантийных
течений и скорость перемещения континента постоянно меняются. По
прошествии времени порядка 1.5 10
9 лет, пройдя расстояние около 15 тыс
км, континент оказывается на месте, где сконцентрировано несколько
холодных нисходящий мантийных потоков. Тогда скорость континента
резко уменьшается и он, в зависимости от общей структуры мантийных
течений, может продолжить свое движение как в первичном, так и в
обратном направлении. Результаты проведенного численного
эксперимента могут быть использованы для анализа механизма дрейфа
континентов типа Евразии, зарождения и подьема плюмов и
геодинамических процессов в субконинтальной мантии.
80. В
мантии устанавливается развитая нестационарная тепловая конвекция
с узкими нисходящими и восходящими потоками в виде плюмов со
скоростями мантийных течений от 1 до 10 см/год. Далее в некоторый
момент в мантию помещается континент в виде тонкой длинной
пластины толщиной
d =0.03 и длиной
l =2.0 от толщины всей мантии, что
в размерном виде соответственно составляет
d =90 км и l=6 тыс км.
Чтобы продемонстрировать эффект прогревания мантии под
континентом, он помещается на самое холодное место мантии, где в
данный момент оказалось больше нисходящих мантийных потоков.
Эволюция системы мантия-континент находится численным решением
уравнений переноса импульса, массы и тепла для вязкой жидкости и
твердого континента. Дается строгая формулировка задачи, приводится
самосогласованный метод решения полной системы связанных
интегродифференциальных уравнений и указывается метод их
численной реализации. Сначала в течение долгого времени (порядка
500 Ma) континент практически остается неподвижным, но в мантии
происходит кардинальная перестройка течений, в результате которой
холодные нисходящие мантийные потоки под континентом
подавляются, а вместо них под континент стягиваются горячие
восходящие потоки. После этого под влиянием результирующей силы
вязкого сцепления с мантийными течениями континент начинает
перемещаться с переменной скоростью в среднем порядка 1 см/год.
При этом в результате механического сцепления и теплового
взаимодействия с движущимся континентом структура мантийных
течений и скорость перемещения континента постоянно меняются. По
прошествии времени порядка 1.5 10
9 лет, пройдя расстояние около 15 тыс
км, континент оказывается на месте, где сконцентрировано несколько
холодных нисходящий мантийных потоков. Тогда скорость континента
резко уменьшается и он, в зависимости от общей структуры мантийных
течений, может продолжить свое движение как в первичном, так и в
обратном направлении. Результаты проведенного численного
эксперимента могут быть использованы для анализа механизма дрейфа
континентов типа Евразии, зарождения и подьема плюмов и
геодинамических процессов в субконинтальной мантии.
К настоящему времени проведено очень много численных экспериментов для исследования тепловой конвекции в мантии Земли. На двух и трехмерных моделях в декартовой и сферической системе координат выяснена роль переменной вязкости, зависящей от температуры, давления и напряжения и влияние фазовых переходов на структуру мантийных течений. См., например, [Christensen, 1983, 1984; Christensen and Yuen, 1984; Glatzmaier, 1988; Machetel and Weber, 1991; Lenardic and Kaula, 1994; Solheim and Peltier, 1994; Tackley et al., 1994; Parmentier et al., 1994]. Численное моделирование дало возможность понять многие принципиальные закономерности глобальной геодинамики. Важнейшей задачей численного моделирования в ближайшее десятилетие будет построение моделей, в которых высокая вязкая океаническая литосфера самосогласованно разбивается на отдельные плиты.
Другой важной задачей является выяснение влияния континентов на структуру мантийной конвекции. Континенты покрывают более четверти поверхности Земли. Мантийный тепловой поток выходящий из мантии через континенты примерно равен 30 мвт/м 2 , что в три раза меньше, чем теплового потока, выходящего через океаны, в среднем равного 90 мвт/м 2. Это объясняется тем, что континенты теплоэкранируют мантию, так как внутри континентов тепло переносится только кондуктивно. Число Нуссельта, характеризующее ковективный вынос тепла, для всей мантии по разным оценкам может быть порядка 20. Океаническая литосфера участвует в конвективном кругообороте вещества мантии, находясь практически в конвективном тепловом погранслое, и несмотря на высокую вязкость, не сильно теплоэкранирует мантию. Таким образом, даже неподвижные континенты должны существенно влиять на структуру мантийной конвекции.
В работе [Christensen, 1983] на упрощенной модели сравнивалась структура мантийных течений под континентами и океанами. В работе [Трубицын и Фрадков, 1985] показано, тепловая конвекция в верхней мантии подавляется и соответственно уменьшается (в три раза) тепловой поток, выходящий через континенты. В работах [Trubitsyn et al., 1993a, 1993b , 1994; Trubitsyn and Bobrov, 1993; 1996, 1997; Lowman and Jarvis, 1993, 1995, 1996; Bobrov and Trubitsyn, 1996; Nakakuki et al., 1997] показано, что неподвижный континент сначала подавляет мантийную конвекцию под собой и расширяет конвективную ячейку, а затем через время в несколько сот миллионов лет, после прогрева субконтинентальной мантии, под континентом возникает горячий восходящий мантийный поток.
Поскольку континенты не фиксированы в пространстве, а плавают по мантии, то их влияние на структуру мантийной конвекции оказывается еще более сильным. В первых работах влияние движения континентов учитывалось упрощенно в виде эффективного граничного условия. Вместо континента в соответствующих точках на верхней границы, условия свободной границы заменялось заданием горизонтальной скорости [Lux et al., 1979]. В работе [Doin M.-P., 1997] таким же образом эффект движущихся континентов учитывался заданием скорости на верхней границе виде некоторой функции времени.
В работе [Gurnis, 1988] приведены результаты расчета самосогласованной численной двумерной модели мантийной конвекции со свободно плавающими континентами. В работах [Trubitsyn and Rykov, 1995; Rykov and Trubitsyn, 1996a, 1996b] построена первая трехмерная численная модель мантийной конвекции с двумя плавающими континентами. Эта модель [Trubitsyn and Rykov, 1995] воспроизводит общие закономерности формирования и распада Пангеи. После распада Пангеи образуются структуры подобные Атлантическому и Тихому океанам. При этом на окраинах Тихого океана возникают зоны субдукции с почти вертикальным погружением (типа Курило-Камчатки) на одной окраине и очень пологим погружением (типа Южноамериканской) на другой окраине океана. В работе [Rykov and Trubitsyn, 1996b] при другом начальном положении континентов после распада суперконтинента сформировалась структура двух сцепленных континентов, подобная Северной и Южной Америке.
В работе [Trubitsyn and Rykov, 1997] проведено численное моделирование самосогласованной численной модели конвекции в верхней мантии (при невысоких числах Рэлея) с переменной вязкостью и взаимодействующей с движущимся континентом. Континент моделировался толстой твердой плитой. Рассматривались случаи, когда плита могла свободно плавать в мантии и двигаться с заданной фиксированной скоростью. Оказалось, что при приближении к нисходящему холодному мантийному потоку континент отклоняет его, образуя структуры, подобные наклонным зонам субдукции. Угол наклона от горизонтали для нисходящего мантийного потока растет с ростом скорости надвигающегося континента.
В настоящей работе подробно описывается математическая
постановка задачи и метод ее решения. Рассматривается более близкая
к реальной Земле модель конвекции при числе Рэлея Ra=10
6 на сетке
200
 80 с тонким континентом толщиной
d=90 км и горизонтальным
размером
l=6 тыс. км. Рассчитывается длительная эволюция системы
мантия-континент. Из сравнения эволюции нестационарной конвекции
в мантии без континента и с континентом в те же моменты времени
видно, что движущийся континент кардинально изменяет структуру
мантийной конвекции.
80 с тонким континентом толщиной
d=90 км и горизонтальным
размером
l=6 тыс. км. Рассчитывается длительная эволюция системы
мантия-континент. Из сравнения эволюции нестационарной конвекции
в мантии без континента и с континентом в те же моменты времени
видно, что движущийся континент кардинально изменяет структуру
мантийной конвекции.
Мантия моделируется несжимаемой жидкостью с постоянной вязкостью, находящейся в вытянутой\linebreak прямоугольной двумерной области толщиной D и длиной L с аспектным отношением L:D=10:1. Все границы области считаются непроницаемыми с проскальзыванием, кроме верхней свободной границы. Температура на нижней и верхней границах фиксирована и соответственно равна T=T0 и T=0 , что соответствует нагреву снизу. Боковые стенки полагаются теплоизолированными. Начало координат выбирается в левом нижнем углу и ось z направлена вверх, ось x направлена вправо.
Континенты выбираются в виде легких твердых толстых теплопроводных прямоугольных плит длиной l и толщиной d+d0 , плавающих в мантии, где d - глубина погружения в мантию и d0 - высота континентов над мантией. Благодаря силам вязкого сцепления с мантийными течениями континент дрейфует, в сторону нисходящих мантийных потоков. Так как тепло внутри континентов переносится только кондуктивно, континенты создают теплоэкранирущий эффект, задерживая выход тепла из мантии. Кроме того, континенты влияют на мантию и механически, так как благодаря прилипанию выравнивают между собой скорости мантийных течений, примыкающих к торцам и нижней поверхности континентов.
Тепловая конвекция вязкой мантии описывается распределением вектора конвективных скоростей Vi(x, y, z) , распределением температуры T(x, y, z) и давления p(x, y, z). Эти неизвестные функции находятся из решения системы трех уравнений переноса импульса, тепла и массы
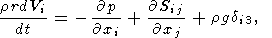 | (1) |
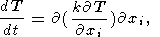 | (2) |
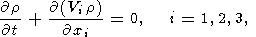 | (3) |
где r - плотность, g - ускорение силы тяжести, T - температура, отсчитываемая от адиабатического распределения , k - коэффициент температуропроводности, dij - символ Кронеккера , Sij - девиаторный тензор вязких напряжений
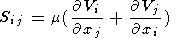 | (4) |
где
m - вязкость. Относительная величина инерциальных
членов в левой
части уравнения переноса импульса в мантии (1) по отношению к
членам в правых частях уравнений имеет порядок
kr /m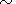 10-23 .
Поэтому этими инерциальными членами можно пренебречь.
10-23 .
Поэтому этими инерциальными членами можно пренебречь.
Положим
r = r0(1
- a) в последнем члене плавучести уравнения (1)
и
r = r0
во всех остальных членах уравнений (1)-(3). Далее будем
отсчитывать давление от его гидростатического распределения
p0(z) ,
определяемого условием
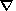 p = -r0g
. Введем безразмерные переменные,
принимая за единицу измерения для длины толщину мантии
D , для
скорости
k/D , для времени
D2/k , для температуры
T0, для вязкости
m ,
для давления и напряжений
mk/D2.
p = -r0g
. Введем безразмерные переменные,
принимая за единицу измерения для длины толщину мантии
D , для
скорости
k/D , для времени
D2/k , для температуры
T0, для вязкости
m ,
для давления и напряжений
mk/D2.
В этих переменных уравнения конвекции (2)-(4) для двумерной модели примут вид :
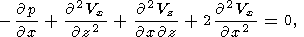 | (5) |
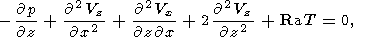 | (6) |
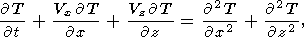 | (7) |
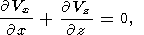 | (8) |
где Ra - число Рэлея, равное
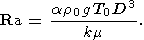 | (9) |
В двумерной модели скорости всех точек твердого континента u=(ux, uy) , плавающего в мантии (вдоль ее горизонтальной поверхности), равны между собой и равны скорости его центра тяжести
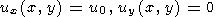 | (10) |
Континенты движутся под действием вязких сил мантийных течений. Уравнение Эйлера для горизонтального движения твердого континента имеют вид
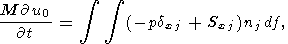 | (11) |
где df - площадь элемента поверхности, nj - единичный вектор внешней нормали к нему, M - безразмерная масса континента, (для рассматриваемой двумерной модели) приходящаяся на единицу длины в направлении оси y. Интеграл берется по всей поверхности погруженной в мантию части континента, включая его подошву (z=1-d) и торцы ( x=x1 и x=x1+l ).
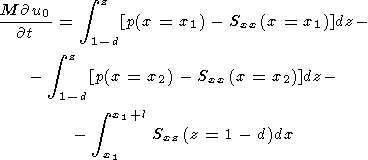 | (12) |
где d и l - толщина и длина погруженной части континента, x1(t) и x2(t)=x1(t)+l - мгновенные координаты левого и правого краев континента, удовлетворяющие условиям
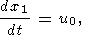 | (13) |
Уравнение для распределения температуры Tс внутри твердого континента в исходной неподвижной системе координат сводится к уравнению теплопроводности c адвективным переносом тепла со скоростью континента u0 вдоль оси x
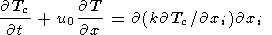 | (14) |
Относительная величина инерциальных членов в левой части
уравнения движения континентов (12) по отношению к членам в
правой части также как и для мантии имеет порядок
kr/m 10-23.
Подставляя выражение (4) для девиаторного тензора вязких
напряжений в уравнения движения континентов (12) и пренебрегая
инерциальными членами, уравнения движения континента в
безразмерных переменных можно записать в виде
10-23.
Подставляя выражение (4) для девиаторного тензора вязких
напряжений в уравнения движения континентов (12) и пренебрегая
инерциальными членами, уравнения движения континента в
безразмерных переменных можно записать в виде
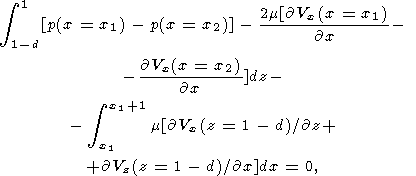 | (15) |
где координата x1 , входящая в пределы интегрирования, определяется из уравнения (13).
Уравнения мантийной конвекции (6-10) и уравнения для движения континента (15, 13) и переноса тепла в нем (14) оказываются взаимосвязаны между собой через граничные условия.
Граничные условия для температуры на нижней и боковых границах всей расчетной области имеют вид :
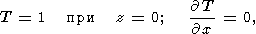 | (16) |
при x=0 и x=10.
На верхней свободной поверхности при z=1 температура мантии равна нулю ( T=0 ) только в океанической области вне континента, то-есть при x < x1(t) и x > x1(t)+l .
На поверхности погруженной в мантию части континента принимаются условия непрерывности температуры и теплового потока между мантией и континентом, то есть на подошве континента при z=1-d и x1(t) < x < x1(t)+l получаем:
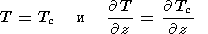 | (17) |
и на торцах континента при 1-d < z < 1 и x = x1 или x = x2
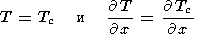 | (18) |
На верхней поверхности континента принимается условие нулевой
температуры, то есть
Tc = 0 при
x1(t) < x < x1(t)+l и
z=1 + d0 , где
d0 - высота
выступающей над мантией части континента. Обычно
d0 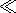 d.
d.
Как указывалось выше, для мантийных течений на нижней и боковых границах всей расчетной области принимаются условия непротекания и проскальзывания. Поэтому на нижней границе можно записать Vz = 0 , Sxz = 0 при z = 0. Так как это условие выполняется при всех x , то и Vz/x = 0 при z = 0. Учитывая соотношение (4), получаем
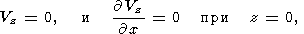 | (19) |
Аналогично для боковых границ области получаем
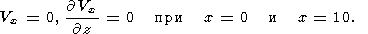 | (20) |
Такое же условие (19) принимается и на верхней свободной поверхности при z=1, но только вне континента,
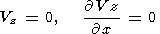 | (21) |
при x < x1(t) и x > x1(t)+l. Условие прилипания вязкой мантии к движущемуся континенту сводится к равенству скорости мантийного течения и скорости движения континента в местах их соприкасания в данный момент
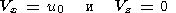 | (22) |
на подошве континента при x1(t) < x < x1(t) + l , z = 1 - d , и на его торцах при 1-d < z < 1 , x = x1 и x = x2.
Условия (22) позволяют упростить уравнение движения континента.
Так как условие непротекания
Vz = 0 выполняется вдоль всей подошвы
континента независимо от
x , то на ней и
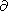 Vz/
Vz/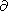 x = 0. Поэтому в (15)
последний член под интегралом обращается в нуль. Аналогично, так
как условие прилипания
Vz = 0 выполняется вдоль всех торцов
континента независимо от
z , то
x = 0. Поэтому в (15)
последний член под интегралом обращается в нуль. Аналогично, так
как условие прилипания
Vz = 0 выполняется вдоль всех торцов
континента независимо от
z , то
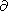 Vz/
Vz/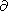 z=0. Но тогда из условия
несжимаемости (8) следует, что вдоль торцов и
z=0. Но тогда из условия
несжимаемости (8) следует, что вдоль торцов и
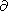 Vx/
Vx/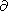 x=0. В результате
уравнения движения континента принимают простой вид :
x=0. В результате
уравнения движения континента принимают простой вид :
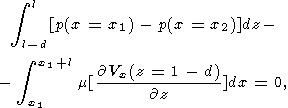 | (23) |
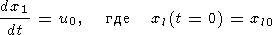 | (24) |
Таким образом, математическая проблема сводится к следующему. Имеется всего семь неизвестных функций. Четыре функции координат и времени для мантийной конвекции: две компоненты скоростей мантийных течений Vx(x, z, t) и Vz(x, z, t) , распределение температуры T(x, z, t) и распределение давления p(x, z, t). Три неизвестные функции времени для континента : распределение температуры в нем Tс(x, z, t) , мгновенная скорость поступательного движения континента как целого u0(t) и координата его левого края x1(t). Для нахождения этих функций имеется замкнутая система семи взаимосвязанных уравнений: четырех дифференциальных уравнения конвекции (5-8), уравнения теплопроводности для континента (14), уравнения движения твердого континента, сводящегося к условию на производные для скоростей мантийных течений (23) и соотношения (24) между скоростью континента и его положением. Для определения постоянных интегрирования дифференциальных уравнений служат граничные условия (18-22).
Отличие рассматриваемой задачи со свободно плавающим континентом от известной задачи с неподвижным континентом состоит в том, что граничные условия непротекания и прилипания на поверхности контакта в каждый момент ставятся в месте нахождения плавающего континента, скорость и положение которого заранее не известны, а на каждом шаге по времени определяются из решения системы взаимосвязанных дифференциальных уравнений.
При численном решении системы уравнений тепловой конвекции с плавающими континентами можно воспользоваться двумя принципиально различными методами. В методе двух областей [Trubitsyn and Bobrov, 1996, 1997] на каждом временном шаге отдельно решаются уравнения тепломассопереноса в мантии вне континента и внутри континента, а затем решения "сшиваются'', чтобы удовлетворить граничным условиям на погруженной в мантию части континента. В методе сквозного счета [Trubitsyn and Rykov, 1995; Rykov and Trubitsyn, 1996a, 1996b] рассматривается единая расчетная область, но на поверхности континента явно учитывается скачек параметров, характеризующих различающиеся между собой свойства вещества мантии и континентов. В методе сквозного счета процедура численного алгоритма более проста, но при этом необходимо проводить сглаживание скачков функций, заменяя на каждом временном шаге твердый континент высоковязкой областью.
В общем виде алгоритм численного счета системы уравнений тепловой конвекции с плавающими континентами сводится к следующему. Пусть в некоторый момент времени t1 нам известны скорости конвективных течений, поле температур T(t1) и давлений p(t1) в мантии, а также положение x1(t1) и скорость континента u0(t1). Нам нужно найти решение системы уравнений (5-8, 14, 23 и 24) в следующий момент времени t2 = t1 + Dt. Новое положение континента x1(t2) в момент t2 можно просто найти по (24) x1(t2) = x1(t1) + u0(t)1)Dt. Если бы была известна также и новая скорость континента в этом положении u0(t2) , то можно было бы решить уравнения тепловой конвекции (5-8) с граничными условиями для температуры (18) и скоростей (19-22), соответствующими новому положению континента, и найти скорости мантийных течений Vx(t2) и Vz(t2), температуру T(t2) и давление p(t2) в момент времени t2. Но сложность задачи как раз и состоит в том, что именно эта скорость континента u0(t2) неизвестна. Она должна быть такой, чтобы новые найденные скорости мантийных течений Vx(t2) и Vz(t2) , соответствующие этой новой скорости u0(t2) , удовлетворяли бы также уравнению движения континента (24). Поэтому необходимо найти какой-либо итерационный способ нахождения этой скорости континента. В принципе можно просто по определенной схеме перебирать значения скорости континента, рассчитывая поля конвективных скоростей и вычисляя интегралы в (23), пока не найдется то значение u0(t2) , при котором правая часть соотношения (23) отличается он нуля на значение e, соответствующее наперед заданной точности. Так как по физическому смыслу правая часть соотношения (23) соответствует силе, действующей на континент, то e > 0 , если выбранная скорость континента u0(t2) занижена и e< 0 , если u0(t2) - завышена.
Решение системы уравнений тепловой конвекции с плавающими континентами проводилось методом конечных разностей [Rykov and Trubitsyn, 1996b].\linebreak При численном решении уравнения переноса температуры (7, 14) использовался метод переноса с коррекцией потоков Залесака [Zalesak, 1979]. Уравнения для скоростей и давления (5, 6, 8) сводились к уравнениям эллиптического типа с переменными коэффициентами (обобщенным уравнениям Пуассона). Для их решения использовался попеременно треугольный метод в трехслойной модификации с выбором итерационных параметров по методу сопряженных градиентов [Samarskii and Nikolaev, 1978].
Мантия моделировалась вязкой жидкостью, находящейся в
вытянутой двумерной области. Толщина мантии
D  3 тыс. км, длина
внешней окружности
2pR
3 тыс. км, длина
внешней окружности
2pR  40 тыс. км., длина внутренней окружности
2p (R-D)
40 тыс. км., длина внутренней окружности
2p (R-D)  21 тыс км. Поэтому приближено была взята область с
аспектным соотношением сторон
L:D = 10:1. Была рассмотрена
простейшая модель с нагревом снизу при числе Рэлея Ra=
106 с
расчетной сеткой
200
21 тыс км. Поэтому приближено была взята область с
аспектным соотношением сторон
L:D = 10:1. Была рассмотрена
простейшая модель с нагревом снизу при числе Рэлея Ra=
106 с
расчетной сеткой
200 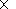 80.
80.
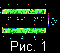
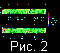
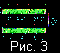
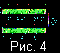 На рис. 1a,
2a,
3a, и
4a представлены результаты расчета мантийной
тепловой
конвекции, возникшей через безразмерное время t=1.0995. Как
известно при
t > 1 даже в отсутствие конвекции вся область
прогревается. Поэтому можно считать, что к рассматриваемому
моменту конвекция полностью установилась. Но при числе Рэлея Ra
> 2105 тепловая конвекция оказывается нестационарной,
квазитурбулентной. Это обусловлено тем, что нелинейные члены
Vx
На рис. 1a,
2a,
3a, и
4a представлены результаты расчета мантийной
тепловой
конвекции, возникшей через безразмерное время t=1.0995. Как
известно при
t > 1 даже в отсутствие конвекции вся область
прогревается. Поэтому можно считать, что к рассматриваемому
моменту конвекция полностью установилась. Но при числе Рэлея Ra
> 2105 тепловая конвекция оказывается нестационарной,
квазитурбулентной. Это обусловлено тем, что нелинейные члены
Vx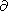 T/
T/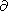 x и
Vz
x и
Vz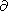 T/
T/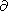 z в уравнении (7)
на каждом временном шаге
генерируют новые более мелкие гармоники. С ростом числа Рэлея эти
нелинейные члены растут и в результате самоорганизации возникают
более мелкие неоднородности, постоянно изменяющиеся со временем.
z в уравнении (7)
на каждом временном шаге
генерируют новые более мелкие гармоники. С ростом числа Рэлея эти
нелинейные члены растут и в результате самоорганизации возникают
более мелкие неоднородности, постоянно изменяющиеся со временем.
Безразмерная температура, равная
T=0 на верхней поверхности и
равная
T0=1 на нижней поверхности области, на рисунках обозначена
цветными тонами. Величина и направление скорости мантийных
течений в каждой точке обозначены стрелкой. Масштаб скоростей
приведен в нижнем левом углу рисунков. Максимальные скорости
мантийных имеют порядок
V max  1500
безразмерных единиц.
1500
безразмерных единиц.
В верхней части рисунков красной линией приведено вычисленное
распределение числа Нуссельта (безразмерного теплового потока
q = -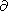 T/
T/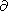 z ) на внешней поверхности области. Среднее значение числа
Нуссельта, примерно, равно Nu
z ) на внешней поверхности области. Среднее значение числа
Нуссельта, примерно, равно Nu
 17. Амплитуда относительных
вариаций теплового потока имеет порядок 100%.
17. Амплитуда относительных
вариаций теплового потока имеет порядок 100%.
Зеленой линией обозначен вычисленный рельеф, то есть
деформации верхней свободной поверхности, возникающие под
действием сил вязких напряжений конвективных течений. Высоты
рельефа приведены на правой оси в безразмерных единицах,
умноженных на
10-3. Высоты рельефа вычисляются по формуле
h = Szz/rg.
Учитывая выражения указанные выше (в параграфе 3) единицы
измерения для компонент тензора напряжений, для единицы измерения
высоты рельефа получим
mk/(rgD2).
Как видно из
рис. 1a,
2a,
3a, и
4a средние
значения амплитуд вычисленных безразмерных высот рельефа имеют
порядок
25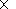 103.
103.
Полагая для Земли
D  3 106 м,
a
3 106 м,
a 3 10-5
К
-1 ,
DT
3 10-5
К
-1 ,
DT  2 103 К,
k
2 103 К,
k  10-6 м
2 с
-1 ,
m
10-6 м
2 с
-1 ,
m 1022
Па с,
r
1022
Па с,
r 5 103
кг/м
3 ,
g
5 103
кг/м
3 ,
g  10 мс
-2, найдем значения
единиц измерения времени и скорости. Для скорости единица
измерения равна
k/D
10 мс
-2, найдем значения
единиц измерения времени и скорости. Для скорости единица
измерения равна
k/D  10-5
м/год, для времени
t=D2/k
10-5
м/год, для времени
t=D2/k  300 млрд. лет.
Число Рэлея, характеризующее интенсивность мантийной тепловой
конвекции, по (9) будет равно Ra
300 млрд. лет.
Число Рэлея, характеризующее интенсивность мантийной тепловой
конвекции, по (9) будет равно Ra
 8 106.
8 106.
Поскольку указанные параметры Земли пока известны еще не
достаточно точно, то при расчетах было взято округленное значение
числа Рэлея Ra =
106. Так как скорости мантийных течений
пропорциональны
V 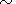 Ra
2/3 [Turcotte and Schubert, 1982],
то значение
вычисленных скоростей и времен легко пересчитать на несколько
отличные числа Рэлея. При сравнении результатов расчета с
наблюдаемыми данными при для Земли с указанными выше
параметрами, нужно значение скоростей
V умножить на
82/3 = 4 , а
значение времени
t разделить на 4. В результате для максимальных
мантийных течений получим
V max
Ra
2/3 [Turcotte and Schubert, 1982],
то значение
вычисленных скоростей и времен легко пересчитать на несколько
отличные числа Рэлея. При сравнении результатов расчета с
наблюдаемыми данными при для Земли с указанными выше
параметрами, нужно значение скоростей
V умножить на
82/3 = 4 , а
значение времени
t разделить на 4. В результате для максимальных
мантийных течений получим
V max  1500
1500 4
4 10-5 м/год
10-5 м/год
 6 см/год.
6 см/год.
На рис. 1a,
2a,
3a, и
4a представлена рассчитанная эволюция мантийной
конвекции для большого интервала времени. Безразмерное время
указано в левой части рисунков. Как указывалось выше, единица
измерения времени равна
t 300 млрд.
лет. Чтобы рассчитать интервал
времени между различными состояниями мантийной конвекции,
приведенным на рисунках, нужно указанные на рисунках безразмерное
время умножить на 300 млрд. лет и (с учетом пересчета чисел Рэлея)
разделить на 4, то есть умножить на 75 млрд. лет. Так полное время
эволюции мантийной конвекции, показанной на рисунках, составляет
(1.1495-1.0995)
300 млрд.
лет. Чтобы рассчитать интервал
времени между различными состояниями мантийной конвекции,
приведенным на рисунках, нужно указанные на рисунках безразмерное
время умножить на 300 млрд. лет и (с учетом пересчета чисел Рэлея)
разделить на 4, то есть умножить на 75 млрд. лет. Так полное время
эволюции мантийной конвекции, показанной на рисунках, составляет
(1.1495-1.0995)  75 млрд. лет
75 млрд. лет
 3.6 млрд. лет.
3.6 млрд. лет.
Для указанных выше параметров Земли единица измерения высот
рельефа будет равна
mk/(rgD2)
 0.02 м. Поэтому рассчитанные
безразмерные амплитуды высот рельефа
2.5
0.02 м. Поэтому рассчитанные
безразмерные амплитуды высот рельефа
2.5  104 , будут
соответствовать значениям 0.5 км.
104 , будут
соответствовать значениям 0.5 км.
На рис. 1b,
2b,
3b, и
4b представлены результаты расчета структуры
мантийных течений с учетом теплового и механического
взаимодействия с движущимся континентом. Для удобства сравнения
рис. 1a,
2a,
3a, и
4a и
рис. 1b,
2b,
3b, и
4b соответствуют
одним и тем же моментам времени.
В момент безразмерного времени
t=1.0995 помещается континент в
виде твердой пластины толщиной
d=0.03
D=90 км и длиной
l=2
D= 6
тыс.км. На рис. 1b,
2b,
3b, и
4b континент указан серым тоном. В качестве
начального положения для континент специально выбирается самое
холодное место в мантии, где сосредоточено наибольшее количество
исходящих мантийных потоков. Как видно из рисунков, благодаря
теплоэкранирующему эффекту мантия под континентом постепенно
прогревается. К моменту безразмерного времени
t=1.1151  1.2 млрд.
лет под континентом возникает четко выраженная система горячих
восходящих мантийных потоков и континент начинает перемещаться
вправо под влиянием результирующей силы вязкого сцепления с
мантийными течениями. Так как континент постоянно взаимодействует
с мантийными течениями, то мере движения континента меняется и
структура мантий конвекции. При дрейфе скорость континента в
безразмерных единицах сначала растет от 100 до 400, а затем опять
уменьшается. В размерных единицах, как указывалось выше, эти
скорости будут равны от 0.4 см/год до 1.6 см/год. Как видно из рис. 1b,
2b,
3b, и
4b,
пройдя расстояние порядка
5
D
1.2 млрд.
лет под континентом возникает четко выраженная система горячих
восходящих мантийных потоков и континент начинает перемещаться
вправо под влиянием результирующей силы вязкого сцепления с
мантийными течениями. Так как континент постоянно взаимодействует
с мантийными течениями, то мере движения континента меняется и
структура мантий конвекции. При дрейфе скорость континента в
безразмерных единицах сначала растет от 100 до 400, а затем опять
уменьшается. В размерных единицах, как указывалось выше, эти
скорости будут равны от 0.4 см/год до 1.6 см/год. Как видно из рис. 1b,
2b,
3b, и
4b,
пройдя расстояние порядка
5
D  15 тыс.км, через 2 млрд. лет
континент почти останавливается.
15 тыс.км, через 2 млрд. лет
континент почти останавливается.
 Анимационные рисунки в данной онлайновой версии (рис. 5 и рис. 6 по 30 кадров каждый) дополняют серии рис. 1a,
2a,
3a, и
4a и рис. 1b,
2b,
3b, и
4b
соответственно.
Анимационные рисунки в данной онлайновой версии (рис. 5 и рис. 6 по 30 кадров каждый) дополняют серии рис. 1a,
2a,
3a, и
4a и рис. 1b,
2b,
3b, и
4b
соответственно.
Рассчитана эволюция свободной нестационарной мантийной конвекции и эволюция мантийной конвекции, взаимодействующей со свободно плавающим континентом. Сравнение распределений температуры и скоростей мантийных течений для обеих моделей в одни и те же моменты времени показывает, что плавающие континенты принципиально изменяют структуру и эволюцию мантийной конвекции. Рассчитанные скорости мантийных течений и движений континента и распределения теплового потока согласуются с данными наблюдений. Представленные результы детальной эволюции мантийных течений могут быть использованы для анализа механизма дрейфа континентов типа Евразии, зарождения и подьема плюмов и теплового режима субконтинтальной мантии.
Бобров А. М., Трубицын В. П., Времена перестроек мантийных течений под континентами, Физика Земли, N. 7, 1995, c. 5-13.
Рыков В. В., Трубицын В. П., Численное моделирование мантийной конвекции и тектоники континентальных плит, Вычислительная сейсмология, т. 26, Геодинамика и прогноз землетрясений, 1994, c. 94-102.
Рыков В. В., Трубицын В. П., Трехмерная модель мантийной конвекции с движущимися континентами, Вычислительная сейсмология, т. 27, Теоретические проблемы геодинамики и сейсмологии, 1994, c. 21-41.
Самарский А. А., Николаев Е. С., Методы решения сеточных уравнений, Наука, M., 1978, c. 591.
Трубицын В. П., Фрадков А. С., Конвекция под континентами и океанами, Физика Земли, N 7, 1985, c. 3-14.
Трубицын В. Р., Бобров А. М., Кубышкин В. В. Влияние континетальной литосферы на структуру мантийной тепловой конвекции, Физика Земли, N 5, 1993, c. 3-11.
Трубицын В. П., Белавина Ю. Ф., Рыков В. В., Тепловое и механическое взаимодействие мантии с континентальной литосферой, Физика Земли, N 11, 1993, c. 3-13.
Трубицын В. П., Бобров А. М., Эволюция структуры мантийной конвекции после распада суперконтинта, Физика Земли, N 9, 1993, c. 27-37.
Трубицын В. П., Белавина Ю. Ф., Рыков В. В., Тепловая конвекция в мантии с переменной вязкостью и континентальной плитой конечных размеров, Физика Земли, N 7/8, 1994, c. 5-17.
Трубицын В. П., Бобров А. М., Тепловое и механическое взаимодействие континентов с мантией, Вычислительная сейсмология, т. 27, Теоретические проблемы геодинамики сейсмологии, 1994, c. 3-20.
Трубицын В. П., Бобров А. М., Структура мантийной конвекции под неподвижными континентами, Вычислительная сейсмология. Современные проблемы сейсмичности и динамики Земли, N 28, Наука, М., 1996, с. 22-31.
Трубицын В. П., Рыков В. В., Механизм формирования наклонных зон субдукции, Физика Земли, N. 6, 1997, c. 1-12.
Теркотт Д., Шуберт Дж., Геодинамика, Мир, M., 1985, 730 c.
Bobrov. A. M., Trubitsyn V. P., Times of rebuilding of mantle flows beneath continent, Izvestiya, Physiscs of the Solid Earth, 31, 1996, pp. 551-559.
Christensen U., A numerical model of coupled subcontinental and oceanic convection, Tectonophysics, 95, 1983, pp. 1 - 23.
Christensen U. R., Convection wih pressure- and temperature-dependent non-Newtonian rheology, Geophys. J. Astr. Soc., 77, 1984, pp. 343-384.
Christensen U. R. and Yuen D. A., The interaction of a subducting lithospheric slab with a chemical or phase boundary, J. Geophys. Res., 89, 1984, pp. 4389-4402.
Doin M.-P., Fleitout L. and Christensen U., Mantle convection and stability of depleted and undepleted continental lithosphere, J. Geophys. Res., 102, 1997, pp. 2771-2787.
Glatzmaier G. A., Numerical simulation of mantle convection: Time-dependaent, three-dimensional, compressible, spherical shell, Geophys. astrophys. Fluid Dyn., 43, 1988, pp. 223-264.
Guillou, L. and Jaupart C., On the effect of continents on mantle convection, J. Geophys. Res., 100, 1995, pp. 24217-24238.
Gurnis M., Large-scale mantle convection and aggregation and dispersal of supercontinents, Nature, 332, 1988, pp. 696-699.
Gurnis M. and Zhong S., Generation of long wavelengh heterogeneitiey in the mantle dynamics interaction between plates and convection, Geophys. Res. Lett., 18, 1991, pp. 581-584.
Lenardic A. and Kaula W. M., Tectonic plates, D " thermal structure, and the nature of mantle plumes, J. Geophys. Res., 99, 1994, pp. 15697-15708.
Lowman J. P. and Jarvis J. T., Mantle convection flow reversals due to continental collisions, Geophys. Res. Lett., 20, 1993, pp. 2091-2094.
Lowman J. P. and Jarvis J. T., Mantle convection models of continental collision and breakup incorporating finite thickness plates, Phys. Earth Planet. Inter., 88, 1995, pp. 53068.
Lowman J. P. and Jarvis J. T., Continental collisions in wide aspect ratio and high Rayleigh number two-dimensional mantle convection models, J. Geophys. Res., 101, B11, 1996, pp. 25485-25497.
Lux R. A. Davies G. F. and Thomas J. H., Moving lithospheric plates and mantle convection, Geophys. J. R. Astron. Soc., 57, 1979, pp. 209-228.
Machetel P. and Weber P., Intermittent layered convection in amodel mantle with an endothermic phase change at 670 km, Nature, 350, 1991, pp. 55-57.
Nakakuki T. Yuen D. A. and Honda S., The interaction of plumes with the transition zone under continents and oceans, Earth Planet. Sci. Lett., 146, 1997, pp. 379-391.
Parmentier E. M. Sotin C. and Travis B. J., Turbulent 3-D thermal convection in an infinite Prandl number, volumetrically heated fluid; Implication for mantle dynamics, Geophys. J. Int., 116, 1994, pp. 241-254.
Rykov V. V. and Trubitsyn V. P., Numerical technique for calculation of three-dimensional mantle convection and tectonics of continental plates, in Computational Seismology and Geodynamics, v. 3 ed. by D. K. Chowdhury. Am. Geophys. Un., Washington D.C. 1996a. pp. 17-22. (English translation of Vychisliteljnaya seismologiya, Nauka, M., No. 26, 1994, pp. 94-102)
Rykov V. V and Trubitsyn V. P., 3-D model of mantle convection incorporating moving continents, in Computational Seismology and Geodynamics, v. 3 ed. by D. K. Chowdhury. Am. Geophys. Un., Washington D.C., 1996b, pp. 23-32. (English translation of Vychisliteljnaya seismologiya, Nauka, M., No. 27, 1994, pp. 21-41)
Samarskii A. A. and Nikolaev E. S., Method of solving finite-difference equations (in Russian), Nauka, M., 1978, 591 p.
Solheim L. P. and Peltier W. R., Phase boundary deflections at 660-km depth and episodically layered isochemical convection in the mantle, J. Geophys. Res., 99, 1994, pp. 15861-15875.
Tackley P. J., Stevenson D. J., Glatzmaier G. A., Schubert G., Effect of multiple phase transitions in three dimension spherical model of convection in Earth’s mantle, J. Geophys. Res., 99, 1994, pp. 15877-15901.
Trubitsyn V. P. and Fradkov A. S., Convection under continnts and oceans, Izvestiya, Physiscs of the solid Earth, 21, No. 7, 1985, pp. 491-498. (English translation of Fizika Zemli, No. 7, 1985, pp. 3-13. Published by American Geophysical Union and Geological Society of America).
Trubitsyn V. P., Bobrov A. M., and Kubyshkin V. V., Influence of continental lithosphere on structure of mantle thermal convection, Izvestiya, Physiscs of the solid Earth, 29, 1993, pp. 377-385. (English translation of Fizika Zemli, No. 9, 1993, pp. 27-37. Published by American Geophysical Union and Geological Society of America).
Trubitsyn V. V., Belavina Yu. F., Rykov V. V., Thermal and mechanical ineraction of mantle and continental lithosphere, Izvestiya, Physiscs of the solid Earth, 29, 1993, pp. 933-945. (English translation of Fizika Zemli, No. 11, 1993, pp. 3-13. Published by American Geophysical Union and Geological Society of America).
Trubitsyn V. P. and Bobrov A. M., Structure evolution of mantle convection after breakup of supercontinent, Izvestiya, Physiscs of the solid Earth, 29, 1994, pp. 768-778. (English translation of Fizika Zemli, No. 9, 1993, pp. 27-37. Published by American Geophysical Union and Geological Society of America).
Trubitsyn V. V., Belavina Yu. F., Rykov V. V., Thermal mantle convection in a varying viscosity mantle with a finite-sized continental plate, Izvestiya, Physiscs of the solid Earth, 30, 1995, pp. 587-599. (English translation of Fizika Zemli, No. 7/8, 1994, pp. 5-17. Published by American Geophysical Union and Geological Society of America).
Trubitsyn V. P. and Rykov V. V., A 3-D numerical model of the Wilson cycle, J. Geodynamics, 20, 1995, pp. 63-75.
Trubitsyn V. P. and Bobrov A. M., Thermal and mechanical interaction of continents with the mantle, in Computational Seismology and Geodynamics, v. 3, ed. by D. K. Chowdhury. Am. Geophys. Un., Washington D.C, 1996, pp. 33-41. (English translation of Vychisliteljnaya seismologiya, Nauka, M., No. 27, 1994, pp. 3-20).
Trubitsyn V. P and A. M. Bobrov A. M., Structure of mantle convection beneath stationary continents, in Computational Seismology and Geodynamics, v. 4, ed. by D. K. Chowdhury. Am. Geophys. Un., Washington D.C., 1997, pp. 42-53. (English translation of Vychisliteljnaya seismologiya, Nauka, M., No. 28, 1996, pp. 22-31).
Trubitsyn V. P. and Rykov V. V., Mechanism of formation of an inclined subduction zone, Izvestiya, Physics of the Solid Earth, 33, No. 6, 1997, pp. 427-437. (English translation of Fizika Zemli, No. 6, Interperiodica Publishing, 1997, pp. 1-12).
Turcotte D. L. and Schubert G., Geodynamics: Applications of Continuum Physics to Geological Problems, John Wiley, New York, 1982, 449 pp.
Zalesak S. T., Fully multidimensional flux-correced transport algorithms for fluids, J. Comp. Phys., 31, 1979, pp. 335-361.
Zhong S. and Gurnis M., Dynamic feedback between a continentlike raft and thermal convection, J. Geophys Res., 98, 1993, pp. 12219-12232.
Zhong Sh. and Gurnis M., Role of plates and temperature-dependent viscosity in phase change dynamics, J. Geophys. Res., 99, 1994, pp. 15,903-15,917.
 |