Russian Journal of Earth Sciences
Vol. 7, No. 1, February 2005
Medium-term prediction of earthquakes from a set of criteria:
Principles, methods, and implementation
A. D. Zavyalov
Institute of Physics of the Earth, Russian Academy of Sciences,
Moscow, Russia
Contents
Abstract
This paper presents results obtained in 1980-2002 from studies of various
aspects of earthquake prediction in relation to the
development of a method of medium-term prediction from a set of criteria.
1. Introduction
By their catastrophic consequences, number of victims, material damage, and
adverse environmental impact, earthquakes are the most dangerous natural
catastrophes. They are not so dangerous by themselves as due to the fact that
they occur in populated areas. Their sudden onset aggravates even more their
destructive consequences. Damage and casualties are due to not only ground
motions proper but also various secondary natural phenomena activated by
earthquakes (creep, landslides, rockfalls, snowslides, ground liquefaction, and
so on). Secondary anthropogenic effects and aftermath (fires, explosions,
releases of radioactive and toxic matter, and epidemics) are also highly
dangerous.
Such natural phenomena as earthquakes are inevitable and cannot be prevented,
but their destructive effects can and must be mitigated. For this purpose, one
should know origins of earthquake occurrence, study processes related to the
preparation and realization of earthquakes, and develop methods for their
prediction.
Earthquakes account for 13% of total number of natural catastrophes that
occurred in the world from 1965 through 1999, occupying the third place
[Osipov, 2001].
According to data of the National Earthquake Information Center (NEIC) of
the United States, 2000 earthquakes with magnitudes
MS 7.0 occurred in the
world over the 20th century (from 1900 through 1999), and 65 of these had
magnitudes
MS
7.0 occurred in the
world over the 20th century (from 1900 through 1999), and 65 of these had
magnitudes
MS 8.0. Casualties associated
with the earthquakes of the 20th
century amounted to 1.4 million victims. Of this number, 987 thousand casualties
(about 32900 victims per year) account for the last 30 years, when human and
economic losses were fixed more accurately. According to data of the Center for
Research on the Epidemiology of Disasters (CRED) over 1965-1999, among all
natural catastrophes, earthquakes occupy third place by the number of deaths
(17% of the total number).
8.0. Casualties associated
with the earthquakes of the 20th
century amounted to 1.4 million victims. Of this number, 987 thousand casualties
(about 32900 victims per year) account for the last 30 years, when human and
economic losses were fixed more accurately. According to data of the Center for
Research on the Epidemiology of Disasters (CRED) over 1965-1999, among all
natural catastrophes, earthquakes occupy third place by the number of deaths
(17% of the total number).
Over 25% of Russia's area belongs to seismically hazardous zones, where seismic
tremors of an intensity of 7 and more are likely to arise
[Ulomov, 2000;
Ulomov and Shumilina, 1999-2000].
This territory includes 3000 large and small cities
and settlements, 100 large hydro- and thermoelectric stations, 5 nuclear power
plants, and numerous installations of higher ecological hazard. The territory of
103 Russian cities is earthquake prone
[Osipov, 2001;
Ulomov and Shumilina, 1999-2000].
The above implies the importance and relevance of earthquake prediction
as part of a more general task of mitigating the hazard and economic aftermath
of natural catastrophes.
Notwithstanding a great number of precursors, none is capable of giving exact
information on the time, place and strength of a forthcoming earthquake. Various
precursors differ in their behavior in various seismically active regions and
yield a large scatter in estimates of the time, place and strength of a future
earthquake. Note also that reports on earthquake precursors are generally and it
is difficult, if possible at all, to use this evidence for estimating, even
retrospectively, their statistical characteristics such as the probabilities of
correct prediction and false alarm and the average expectation time of an
earthquake after recording of a precursor.
Analysis of long-term data on several geophysical (mostly seismological)
precursors showed that the probability of successive prediction using each of
the precursors does not exceed 0.5
[Zavyalov, 2002].
A possible way out of this situation is the joint use of several prognostic criteria.
Practice of last years showed that, notwithstanding its disadvantages, this approach
is
justified, at least in relation to medium-term (a few years) prediction.
Methods applied to the solution of this problem are based on the following
principles:
- physical substantiation of the precursors in use, implying constraints on the
relation of the precursors to the preparation process gained from theoretical
and experimental results;
- estimation of basic statistical characteristics (probability of correct
prediction, false alarm probability, and so on) and prognostic efficiency of the
precursors used;
- mapping of the precursor values in space and time;
- Bayesian approach to the determination of probabilistic prediction
characteristics in the multiple-criteria approach.
2. Brief Review of Earthquake Prediction Algorithms
An earthquake prediction algorithm is understood here as a sequence of
operations intended for the identification of characteristic criteria or
anomalous variations in rate of geophysical-geological fields and their joint
treatment and analysis for the determination of the place, time and strength of
a future earthquake.
KORA-3 algorithm.
The first stage of scientific research on earthquake
prediction mainly consisted in accumulation of empirical data on phenomena
preceding the onset of strong earthquake and disappearing after its occurrence.
These criteria can be classified as dynamic. A few tens of cases of these
phenomena had been recorded by the late 1960s-early 1970s. On the other hand,
based on a set of geological-morphological and geomorphostructural criteria in
seismically active regions, researchers tried to identify areas capable of
generating strong earthquakes; these criteria can be classified as static.
A theoretical prerequisite for the use of data on contemporary topography was the
idea that large landforms in seismically active regions were produced by
orogenic tectonic processes involving lithospheric depths comparable to
hypocentral depths of earthquakes
[Gelfand et al., 1976a].
For the first time, this problem was formulated as a problem of predicting
places of strong earthquakes by V. I. Keilis-Borok in the early 1970s
[Gelfand et al., 1972a;
Keilis-Borok and Kossobokov, 1984, 1986;
Keilis-Borok et al., 1980;
Rantsman, 2001].
It was attacked not only by geophysicists but also by
geologists and mathematicians (E. Ya. Rantsman, I. M. Gelfand,
Sh. A. Guberman
and M. L. Izvekova)
[Gelfand et al., 1972a, 1973, 1974a, 1974b, 1976].
Afterward, large contributions to the solution of the problem of recognizing places
of
strong earthquake occurrence were made in
[Bhatia et al., 1992;
Caputo et al., 1980;
Cisternas et al., 1985;
Gelfand et al., 1972b, 1976b;
Gorshkov et al., 1979, 1985, 1991, 2001;
Gvishiani et al., 1982, 1984, 1988;
Healy et al., 1992;
Kossobokov and Khokhlov, 1993;
Kossobokov and Rotvain, 1977;
Kossobokov et al., 1990, 1999;
Romashkova and Kossobokov, 2001,
2002;
Zhidkov et al., 1975].
Based on the hypothesis according to which epicenters of the majority of strong
earthquakes gravitate toward morphostructural nodes, the latter were chosen as
objects for recognition. A set of criteria (characteristics of higher and lower
seismic activity of nodes) proved rather extensive, amounting to a few tens of
parameters. All these parameters were geological and characterized intense and
contrasting neotectonic movements and tectonic fragmentation of nodes. Using a
special set of criteria, an algorithm known under the name KORA-3
[Bongard, 1967]
based on the pattern recognition method was first to be trained, i.e. to
select criteria specific to high seismicity nodes ( H ) and to low seismicity
nodes ( L ).
Instrumental data on geophysical and geochemical fields, as well as on weak
seismicity, were not used, although their suitability for recognition was not denied
[Gorshkov et al., 2001].
The authors did not present any physical arguments in favor of one or other criterion
[Gelfand et al., 1972a].
The training procedure used samples of
H and
L nodes at which earthquakes of
predicted magnitudes occurred or, respectively, did not occur in the past.
The second stage consisted in the separation of nodes, at which no strong
earthquakes had been previously recorded, into the
H and
L categories. The
difference ( D ) between the numbers of the
H and
L criteria fixed for a
given node was used as a parameter based on which the node was attributed to the
H or
L type. A threshold value of
D was selected experimentally. The first
results obtained by this technique were published in
[Gelfand et al., 1972a].
Over the period from 1972 through 2000, the recognition procedure was applied to
more than 1100 morphostructural nodes. In all, 68 strong earthquakes occurred
over 30 years in all of the regions studied. 57 (84%) of these events occurred
at nodes that were recognized as
H nodes, 4 (6%) events occurred at
L nodes,
and 7 (10%) events occurred outside the nodes (target missing). Most of the
latter cases were confined to lineament zones.
An advantageous compromise between geomorphological and mathematical methods of
the recognition of possible earthquake occurrence places that was attained in
these studies has given good results. A drawback of this approach is its total
disregard for the time aspect; i.e. places were predicted in which strong
earthquakes of given magnitudes should sooner or later occur. In other words,
the static problem of predicting the place and strength of an earthquake was
solved. The question of the occurrence time (the third component of prediction)
remained open. However, in our opinion, the recognition problem can also be
formulated on the basis of dynamic time-dependent criteria. No theoretical
appear to be present in this way.
Another drawback of this approach is inadequate physical substantiation of the
relation between recognition criteria and the process of the strong earthquake
generation; as mentioned above, we mean the set of principles that are
consistent with theoretical and experimental data, providing constraints on the
relation of precursors to the preparation process.
An advantage of the prognostic procedure based on the KORA-3 algorithm is its
good formal description, admitting an independent verification. We should also
note that KORA-3 was the first algorithm intended for prediction of strong
earthquakes and using a set of prognostic characteristics.
Fortran Generalized Portrayal algorithm.
The inability to predict the
earthquake occurrence time from data on statistical criteria, on the one hand,
and a large number of dynamic prognostic criteria (their recording time was
related, in a way, to the earthquake occurrence time) accumulated by the early
1970s, on the other hand, induced researchers to seek other ways for solving the
pattern recognition problem in order to predict not only the place of a future
earthquake but also the time (or time interval) of its possible occurrence.
In the 1970s, a theory and methods based the pattern recognition techniques were
developed for the reconstruction of time dependences from empirical data
[Vapnik, 1979, 1984;
Vapnik and Chervonenkis, 1974].
Unlike the KORA-3 algorithm, this method is statistical, uses the principle of
empirical risk minimization and, which is important for the prediction problem,
allows one to work with small samples. An algorithm implementing this method was
called the Fortran Generalized Portrayal (FGP) algorithm
[Vapnik, 1984].
The FGP algorithm, implementing the solution to the pattern recognition problem,
is based on the generalized portrayal method of the construction of the
hyperplane separating the space of given criteria into one or other situation
(in the simplest case, into two classes)
[Vapnik, 1979, 1984;
Vapnik and Chervonenkis, 1974].
The generalized portrayal means in this case the
minimum-modulus directing vector of the separating hyperplane. Since all
computer programs implementing the method of generalized portrayal were written
in FORTRAN, this is reflected in the method's name.
The FGP method, intended for the recognition of spatial cells and time intervals
of possible earthquakes of given energy classes, was applied for the first time
to the Caucasus in the early 1990s
[Chelidze et al., 1995;
Construction..., 1991].
Initial data for this study were taken from the Caucasus regional catalog
of earthquakes. The recognition problem was solved with a set of strong
( K 12.5 ) earthquakes (and their groups)
and a set of prognostic criteria determined
from weak seismicity data processing: the recurrence plot slope
g,
density of seismogenic faults
Ksf, number of earthquakes
n, and released
seismic energy
E2/3. All criteria were represented as deviations of their
current values from their long-term (background) values and were normalized to
the rms error of the determination of the long-term series average. Values of
these parameters were calculated in a moving time window
DT=3 years long with
a step of
Dt=3 months in rectangular cells 50
12.5 ) earthquakes (and their groups)
and a set of prognostic criteria determined
from weak seismicity data processing: the recurrence plot slope
g,
density of seismogenic faults
Ksf, number of earthquakes
n, and released
seismic energy
E2/3. All criteria were represented as deviations of their
current values from their long-term (background) values and were normalized to
the rms error of the determination of the long-term series average. Values of
these parameters were calculated in a moving time window
DT=3 years long with
a step of
Dt=3 months in rectangular cells 50
 50 km and 100
50 km and 100
 100 km
in size with a half-size overlapping. The informativeness of each criterion was checked
separately before applying the recognition procedure to the set of criteria.
100 km
in size with a half-size overlapping. The informativeness of each criterion was checked
separately before applying the recognition procedure to the set of criteria.
The recognition problem was formulated in terms of the identification of higher
seismic hazard (HSH) time intervals. A six-year interval preceding a strong
earthquake was specified for each cell in which such an earthquake occurred.
Results of the HSH time interval recognition based on the use of the precursor
g and the joint use of the parameters
g and
E2/3 showed that correct
recognition of the
K 12.5 earthquake occurrence was attained
in 74% of all cases.
12.5 earthquake occurrence was attained
in 74% of all cases.
The method of the HSH time interval identification based on the FGP algorithm is
devoid of the main drawbacks of the method using the KORA-3 algorithm and is
effective for predicting not only the place and strength of a future earthquake
but also the time (time interval) of its occurrence. Moreover, parameters used
as precursors have a clear physical meaning and are related to the preparation
process. Unfortunately, the FGP method has not been further developed in
relation to earthquake prediction problems. This was largely due to the breakup
of the USSR and the loss of scientific contacts in the mid-1990s.
Complex of the California-Nevada (CN), magnitude 8 (M8)
and Mendocino scenario
(MSc).
These algorithms were designed and developed in
[Allen et al., 1984, 1986;
Keilis-Borok and Kossobokov, 1984, 1986].
These algorithms continue and develop approaches underlying the problem previous
formulated for the recognition of possible strong earthquake occurrence places
[Gelfand et al., 1972a].
They realize prediction of not only the place but also the time and
magnitude of a potential earthquake. The development of the CN, M8 and MSc
algorithms was apparently stimulated by the inability of the KORA-3 algorithm to
predict the earthquake occurrence time. They use a complex of prognostic
criteria determined primarily from data on seismicity.
A final goal of all algorithms is the determination of times of increased
probability (TIP) for predicting strong earthquakes with magnitudes
M M0 based on analysis
of a complex of earthquake flow properties. Values of
precursory parameters were calculated from data of a catalog of earthquakes,
aftershocks of which were preliminarily removed by the method proposed in
[Keilis-Borok et al., 1980].
The CN and M8 algorithms used the same set of formal prognostic criteria
determining various properties of the earthquake flow
[Sadovsky, 1986].
The physical meaning of the prognostic functions in use and
their relation to earthquake preparation processes were not considered by the
authors of the algorithms, who were mainly guided by the experience of
retrospective statistical analysis of catalogs. The strong earthquake magnitude
value
M0 varied from one region to other but was not lower than 6.4.
M0 based on analysis
of a complex of earthquake flow properties. Values of
precursory parameters were calculated from data of a catalog of earthquakes,
aftershocks of which were preliminarily removed by the method proposed in
[Keilis-Borok et al., 1980].
The CN and M8 algorithms used the same set of formal prognostic criteria
determining various properties of the earthquake flow
[Sadovsky, 1986].
The physical meaning of the prognostic functions in use and
their relation to earthquake preparation processes were not considered by the
authors of the algorithms, who were mainly guided by the experience of
retrospective statistical analysis of catalogs. The strong earthquake magnitude
value
M0 varied from one region to other but was not lower than 6.4.
Retrospective testing of the CN and M8 algorithms in various seismically active regions
of the world
[Sadovsky, 1986]
has shown the following. 23 of 29 strong earthquakes recorded over the testing time
occurred in the CN
predicted TIP intervals whose overall length amounted to 23% of the total testing
time.
Eight of nine strong earthquakes occurred in the M8 predicted TIP intervals. The
overall length of the latter amounted to 16% of the total testing time, whereas
the overall expectation time accounted for 11%
[Sadovsky, 1986].
Notwithstanding good results of its application, the CN algorithm has not been
further used. This might be attributed, among other factors, to the fact that
the alarm state was declared in this algorithm over large territories (a few
hundred thousands of squared kilometers).
Although the same drawback characterizes the M8 algorithm,
Healy et al. [1992]
and Kossobokov and Khokhlov [1993]
reported on the beginning of experimental
medium-term prediction of
M 7.5 earthquakes that would be conducted
in a
real-time mode with the use of the M8 algorithm. This experiment is still
continuing.
7.5 earthquakes that would be conducted
in a
real-time mode with the use of the M8 algorithm. This experiment is still
continuing.
Large areas of scanning cells in which TIP intervals are sought induced the
authors of the M8 algorithm to develop an auxiliary algorithm reducing the
spatial uncertainty of prediction. This algorithm, called the Mendocino scenario
(MSc)
[Kossobokov et al., 1990],
is applied if a TIP period is diagnosed in a testing area of size
D with the use of
CN or M8. Then, this area is divided into square cells
Sij of the linear size
D/16.
Relative seismic quiescence in the TIP period (with respect to previous time) is
sought
in each of the resulting cells
Sij. The authors of the MSc algorithm note that such anomalous
quiescence periods cannot be identified in a low-activity part of the alarm
territory. Therefore, the MSc algorithm identifies precisely the areas of higher
seismic activity, immediately involved in the earthquake preparation process
[Romashkova and Kossobokov, 2001].
Data of the MSc algorithm testing in both retrospective approach and real-time
mode showed that the MSc application complementing CN and M8 reduces the
spatiotemporal volume of alarm by three to four times for earthquakes of
M0 8 and by seven to eight times
for earthquakes of
M0
8 and by seven to eight times
for earthquakes of
M0 7.5.
7.5.
Thus, all algorithms considered above are based on the recognition of situation
patterns characterized by a set of criteria statistically related to possible
generation of strong earthquakes and their preparation process. The algorithm
outputs present a list of places, zones and territories in which strong
earthquakes of a given magnitude range (KORA-3 algorithm) or a list of time
periods during which strong earthquakes of a given amplitude range can occur in
a certain seismically active territory (FGP, CN and M8 algorithms).
The algorithms use a complex of prognostic characteristics. However, most of the
latter do not have a distinct, physically substantiated relation to the
earthquake preparation process. The authors proceeded from intuitive
considerations that this or other criterion reflects, in a way, the preparation
process. Recognition results obtained by the algorithms confirm these
considerations only statistically but do not clarify the physics of the process itself.
A drawback of the KORA-3 algorithm is its inability to predict the occurrence
time of a strong earthquake. KORA-3 solves a static problem of predicting the
place of a strong earthquake. A significant drawback of the CN and M8 algorithms
consists in large sizes of their spatial scanning cells, which is due to
sufficiently large samples of earthquakes required for effective operation of
the algorithms.
None of the algorithms provides mapped information on the occurrence probability
of a strong earthquake at a given point of the seismically active territory
under consideration.
3. Earthquake Precursors and Physical Principles Underlying
Earthquake
Prediction
Earthquake preparation models.
The majority of preparation models were
developed in the 1950s-1970s. This was primarily associated, on the one hand,
with the interest (increased in the mid-1950s-1960s) to the earthquake prediction
problem and its formulation as a fundamental scientific problem
[Gamburtsev, 1954, 1982]
and, on the other hand, and the discovery of macrofracture
precursors of various physical origins observed in both laboratory experiments
with samples of model materials and in situ investigations in seismically active
regions
[Sadovsky and Nersesov, 1978].
A feature common to the vast majority of the earthquake preparation models was their
qualitative approach to the description of the process
[Zubkov et al., 1980].
Avalanche-unstable fracturing (AUF) model
[Myachkin et al., 1975].
Theoretical and experimental prerequisites of its development were principles of
solid
fracture mechanics based on the kinetic concept of strength
[Zhurkov, 1968;
Zhurkov et al., 1977]
and achievements of observational seismology and other geophysical disciplines.
According to the AUF model, the earthquake preparation process consists of three
stages.
Stage 1: quasi-homogeneous cracking. Growth of existing cracks and formation
of new ones takes place at this stage due to tectonic stresses. This process
promotes the development of initial conditions for the formation of a main
rupture but is not accompanied by phenomena of the precursory type.
Stage 2: avalanche-like interaction of cracks. This stage begins when a
certain critical density of cracks is attained in the preparation volume: the
interaction between the cracks gives rise to cracks of larger sizes and rapid
abrupt variations in local stress fields. This process is accompanied by
variations in integral characteristics of the medium that are observed in
various geophysical fields and are precursors of the nucleating earthquake.
Stage 3: instability stage. Deformations are localized in a narrow region
encompassing the zone of the future main shock; several relatively large cracks
develop in this region. As a result of accelerating growth of deformations in
this region, a stress drop and elastic recovery of physicomechanical properties
are observed in the surrounding volume. The preparation zone divides into
elastic and inelastic subszones. The narrow zone of unstable deformation is
characterized by a higher concentration of fractures, and their set forms the
main fault surface. This fault (the earthquake source) is produced through the
breakage of bridges between large cracks. Qualitatively, this process develops
in a similar way at various scale levels, i.e. the formation of the large main
rupture is advanced by similar acts of smaller fracturing. Later, this was
confirmed under conditions of laboratory experiments, mining operations, and in
situ observations in seismically active regions
[Dyagilev, 1998;
Malovichko et al., 1998;
Zavyalov and Nikitin, 1997a, 1997b].
The scale invariance of the fracture process is an advantage of the AUF model.
Apparently, the AUF model served as a cornerstone of the modern ideas representing
a rock as a block-fragmented hierarchical self-organizing medium
[Sadovsky, 1979;
Sadovsky et al., 1982].
Ideas similar to the AUF model were advanced in works by W. Stuart and B. Brady
in relation to earthquake premonitory processes. As distinct from the AUF model,
the strain localization zone in the model of
Stuart [1974]
coincides with the fault present and fractured rock in the vicinity of the latter
behaves,
on a macroscopic scale, as a material with a dropping stress-strain diagram. The
strain development region in the model of
Brady [1974, 1975, 1976]
is considered as a soft elastic inclusion with lower effective elastic moduli; the
main
rupture develops due to stress redistribution such that a favorably oriented
major crack growth and other cracks close.
The presence or absence of water in the preparation region is inessential for
the AUF, Stuart and Brady models. On the contrary, in the dilatancy-diffusion
(DD) theory of earthquake preparation developed by
Scholz et al. [1973]
and likewise based on the fracturing process, tensile fractures prevail and the
presence of water in rocks of the hypocentral region is a factor of basic
significance.
According to the DD model, macrostresses gradually increase at the first
preparation stage characterized by elastic behavior but neither opening of
existing cracks nor formation of new ones occurs. At sufficiently large values
of differential stresses (larger than 50% of the failure value), numerous
tensile cracks arise and a relative increase in the rock volume (dilatancy) is
observed. Water enters the open pores via diffusion from the ambient medium, the
pore pressure drops, and the strength increases. At the third stage, the
diffusion rate being higher than the dilatancy rate, water migrating from
surrounding rocks is supposed to refill the dilatancy region, restoring various
physical parameters to their initial values. The water filling and the pore
pressure rise reduce the effective confining pressure, which is equivalent to a
decrease in the rock strength. As a result, the growth of tensile cracks
accelerates and they join to form a shear rupture resulting in an earthquake. An
advantage of the DD model is that it provides a mechanism underlying the
dependence of the long-term precursor duration on the strength of an earthquake.
A significant drawback of this model is the absence of a mechanism by which the
accumulated dilatancy cracks join to form the major rupture.
Dobrovolsky [1980]
was first to formulate ideas of a general model containing a
heterogeneity (inclusion) that was later called the consolidation model
[Dobrovolsky, 1991].
The geological medium in this model has a block structure,
and the earthquake preparation process consists of three stages. A specific
feature of the first stage (the regular state) is continuous deformation on a
regional or global scale resulting in relative motions of blocks of various
scales. Continuous deformation, short-lived bonds between neighboring blocks and
their breakage give rise to background seismicity and numerous asynchronous
variations in various geophysical fields. A considerable portion of the energy
of tectonic processes is spent on gradual deformation of the medium in the
regular state phase.
The next phase is consolidation. This phase starts with the formation of a bond
between two blocks. If such a bond is sufficiently strong, it will exist for a
longer time compared to background bonds. Strain rates will decrease in its
vicinity, and conditions for enlargement of the bond area will be created. As a
result, the link between the blocks becomes stronger and other blocks can join
the first two, forming a consolidated region, or a consolidated heterogeneity.
Relative movements of blocks inside this region are significantly smaller,
thereby reducing the seismicity. Note that the existence of the consolidation
process is not based on direct experimental data. The formation and development
of the consolidated inclusion disturbs the pattern of initial motions, which in
turn disturbs the regular pattern of background variations in various
geophysical fields. Mechanical stresses and strain rates are redistributed,
accommodating movements taking place far from the consolidation region, in which
the elastic potential energy is accumulated.
The set of phenomena associated with the consolidation phase is classified as
long-term precursors. Their occurrence time is controlled by the intensity of
tectonic processes and the growth rate of the consolidated region. The
consolidation phase can end with the development of plastic motions on inner
interblock boundaries in the consolidated boundary or with a swarm of weak
earthquakes. As a result, the accumulated elastic potential energy will
decrease. If the decrease in the accumulated energy level is sufficiently large,
precursors of a strong earthquake discovered in the consolidation phase will
prove false.
The third phase is a fracture phase. At a certain stage, the consolidated region
stops growing. This can be related to an unfavorable redistribution of the
strain rate field or the influence of adjacent large consolidated blocks. The
general geotectonic setting plays a decisive role in this case. The consolidated
region is a specific crustal volume whose fracture gives rise to an earthquake.
The fracture phase is distinguished by a breakup of the consolidation region
into its separate constituent elements (blocks). Dobrovolsky notes that the
fracture itself occurs mainly on weakened boundaries of blocks, and a rupture
can develop in these areas in accordance with various models.
The fracture phase divides into
a- and
b-stages. At the
a-stage,
the consolidated region breaks up via plastic movements, foreshocks and major
rupture. Short-term precursors are observed at this stage. The time interval
from the main shock to the end of the fracture phase is called the
b -stage.
At this time, the consolidation region is additionally fractured through
aftershocks and plastic motions. The total elastic potential energy of the
medium drops and the intensity of the aftershock activity slowly decreases. The
medium recovers the phase of regular state and the seismic cycle is accomplished.
A significant advantage of the consolidation model is the possibility of
obtaining numerical estimates of the strain field and related precursors.
The development of a preparation model including a heterogeneity was dictated by
the need for a more general description of the preparation process ignoring
various details specific to the AUF, DD, Stuart, and Brady models. However, this
approach has not clarified the formation mechanism of the major rupture and
conditions favoring its development. There is every reason to believe that the
breakup of the consolidated region complies with the AUF model.
Each of the models presented above has its advantages and drawbacks that
apparently set limits to their possible applications to the interpretation of
observed experimental data. As noted in
[Zubkov et al., 1980],
none of the models can be regarded as preferable. Each of these schemes is
acceptable and realizable under appropriate conditions
[Meredith et al., 1990].
However, in my opinion, the functional treatment of fracturing in its transition
from one
structural level to another and the inherent mechanism of a self-developing
process, proposed in the AUF model
[Myachkin, 1978],
makes this model preferable to the other preparation models.
Unique laboratory experiments on the simulation of the preparation process in a
macrofracture source have been conducted over the last 10-15 years
[Ponomarev, 2003;
Sobolev and Ponomarev, 2003].
The AUF model was carefully tested in these
experiments, and the majority of prognostic features observed during preparation
and development of a macrofracture (earthquake source under conditions of a
seismically active region) were experimentally confirmed. These are the division
of the loaded medium into zones of different stress levels with essentially
different evolutionary patterns of the seismic process, specific behavior of the
velocity ratio
Vp/Vs and the recurrence plot
slope
g, localization of
seismicity in a narrow zone defining the position of the future macrorupture,
and the clusterized fracture of the macrorupture zone. On the other hand,
analyzing several precursors of various types, Dobrovolsky arrived at the
following conclusion important for the subject of this paper: progress in
solving the earthquake prediction problem requires "comprehensive joint analysis
of a complex of premonitory phenomena''
[Dobrovolsky, 1991].
Choice of precursors.
Numerous publications of the 1960s-1990s devoted to
diverse premonitory phenomena have provided evidence on about 1000 cases of
anomalous behavior of various geophysical fields preceding strong earthquakes.
In accordance with physical nature, occurrence time, and variability in space
and time, all precursors can be subdivided into several groups of different sizes
[Sidorin, 1992;
Sobolev, 1993;
Zubkov, 2002].
Analysis of the entire set
of available data on precursors indicates that the vast majority of precursors
are phenomenological, i.e. they simply establish an observation of a geophysical
field anomaly before a given strong seismic event. The pertinent publications
usually do not present data on statistical characteristics of the precursors
because the recorded anomalies are not a result of systematic regular
observations; possible, physically substantiated mechanisms responsible for the
occurrence of precursors are not considered. As regards the precursor occurrence
area, data of observations at individual points (stations) are usually
published.
In order to use a concrete precursor for prediction purposes, its significance,
i.e. the probability that its occurrence before a strong earthquake was
nonrandom, should be estimated using either a priori information or
retrospective experience. Moreover, it is necessary to develop algorithms for
declaring an alarm and estimating the probability of false alarms and missing targets
[Keilis-Borok et al., 1980].
In this respect, we should note that only a
small number of precursors recorded throughout the world have met the formal
criteria developed by the IASPEI subcommission on earthquake prediction
[Wyss, 1991].
The above considerations and the experience of the author in developing
algorithms for the identification of prognostic anomalies suggest that the
choice of precursors usable for the medium-term prediction of earthquakes based
on a complex of prognostic criteria should meet the following requirements:
- clear physical meaning of a prognostic criterion;
- physically substantiated relation of each prognostic criterion to the earthquake
preparation process;
- availability of observation data for each prognostic criterion; these data
should be representative in time (long-terms series of prognostic parameter
values) and in space (the possibility of their mapping);
- availability of a formal procedure for the identification of anomalies in
prognostic parameters based on a model of their behavior during the earthquake
preparation;
- possibility of obtaining estimates for retrospective statistical characteristics
of each precursor: probability of successful prediction (probability of
detection), probability of a false alarm, prognostic efficiency
(informativeness), and so on.
Physically substantiated precursors.
All prognostic criteria described below
belong to the group of seismological parameters estimated from regular
seismological observations. Their values are obtained from data processing of
catalogs of earthquakes in seismically active regions under study.
Density of seismogenic faults
Ksf.
Form the standpoint of the kinetic theory
of strength, fracture of solids is a complex thermal fluctuation process
extended in time. The endurance of a loaded solid is described by Zhurkov's equation
[Zhurkov et al., 1980].
The stage of final macrofracture of a loaded
body is preceded by the stage of formation and accumulation of microcracks with
a characteristic lifetime determined by this equation. If
l is an average
distance between the centers of microcracks that are chaotically distributed in
the sample volume, we have
l=c-1/3, where
c is the concentration of
cracks. On a given structural scale, this distance can be expressed through the
crack size
L as follows:
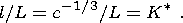 | (1) |
The parameter
K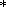 is known as the concentration
criterion of crack enlargement.
Its physical meaning consists in the fact that it characterizes the closeness of
cracks to each other and thereby their interaction and coalescence ability. The
value
K
is known as the concentration
criterion of crack enlargement.
Its physical meaning consists in the fact that it characterizes the closeness of
cracks to each other and thereby their interaction and coalescence ability. The
value
K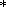 was found to be virtually
constant immediately before macrofracture
for wide ranges of materials (rocks included) and crack sizes (from
microfractures to earthquake-related ruptures in the crust). According to
various estimates of this parameter from data of laboratory and in situ
experiments, the
K
was found to be virtually
constant immediately before macrofracture
for wide ranges of materials (rocks included) and crack sizes (from
microfractures to earthquake-related ruptures in the crust). According to
various estimates of this parameter from data of laboratory and in situ
experiments, the
K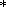 value range from 2.5 to 6.5.
value range from 2.5 to 6.5.
Based on analogies between fracture processes at various scale levels, the
method of concentration criterion of crack enlargement was applied for the first
time to large-scale crustal processes in
[Sobolev and Zavyalov, 1980]
and later in
[Kuksenko et al., 1984].
These studies showed that strong earthquakes mostly
occur in areas of lower values of the concentration criterion. For this reason,
the concentration parameter of seismogenic faults (fractures)
Ksf was
introduced in seismological practice; this parameter characterizes the state of
the seismogenic process in a seismically active crustal volume
V0 at a time
moment
t.
The fracture concentration parameter
Ksf has a clear physical meaning and is
the ratio of the average distance between seismogenic fractures in the volume
V0 to their average length:
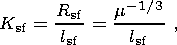 | (2) |
where
m=N/V0 is the volume
density (concentration) of fractures determined by
earthquakes that occurred in the volume,
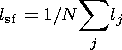 is the fault length average over the ensemble of fractures,
N is the total number
of earthquakes of the energy class range [Kmin, Kmax] that occurred in
the volume
V0 over the time
DT, and
lj is the length of an individual
seismogenic fault.
is the fault length average over the ensemble of fractures,
N is the total number
of earthquakes of the energy class range [Kmin, Kmax] that occurred in
the volume
V0 over the time
DT, and
lj is the length of an individual
seismogenic fault.
Results of analysis of
Ksf spatiotemporal distributions and the experience
of retrospective prediction
[Zavyalov, 1986]
suggest the following scheme of its application to prediction of strong earthquakes.
(i) The distribution of
Ksf is calculated with a step of
Dt for earthquakes
of a given range of energy classes and hypocentral depths in preliminarily
chosen elementary seismically active volumes
Vi.
(ii) If values
Ksf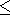 Ksf
al, where
Ksfal is an alarm
level determined experimentally from analysis of retrospective data, are found to
be present
in a certain volume
Vi, the strong earthquake expectation period is declared
for
this volume. The critical level
Ksfal depends on the seismic activity in the
region studied, sizes of the chosen seismically active region, and energy
classes of earthquakes involved in the calculations of
Ksf.
Ksf
al, where
Ksfal is an alarm
level determined experimentally from analysis of retrospective data, are found to
be present
in a certain volume
Vi, the strong earthquake expectation period is declared
for
this volume. The critical level
Ksfal depends on the seismic activity in the
region studied, sizes of the chosen seismically active region, and energy
classes of earthquakes involved in the calculations of
Ksf.
(iii) The expectation state in the volume under consideration
Vi is preserved
during the time period
Texp+|sT| determined
experimentally
from retrospective data. This state can end after a strong earthquake whose hypocenter
is
located in the given seismically active region, whereas in adjacent volumes the
expectation state ends with the onset of aftershock activity.
In the first case, the alarm is regarded as real and the time from the beginning
of the expectation period (the anomaly onset) to the earthquake moment is
defined as the expectation time. In the second case, the alarm declared for
adjacent cells that do not contain the hypocenter is considered false (because
the place of the event formally was not predicted), and the time from the
anomaly onset to the beginning of the aftershock activity is defined as the
false alarm period.
(iv) If a strong earthquake does not occur over the time
Texp+|sT| in the
volume
Vi, this time is classified as the false alarm period.
|
|
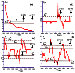
Figure 1
|
A typical plot of
Ksf versus time before a strong earthquake is shown in
Figure 1a.
Recurrence plot slope
g.
This parameter ( b -value) when it is used as a
characteristic of earthquake magnitude) is related to the distribution of
earthquakes over their energies (magnitudes) and is one of main characteristics
of the seismic regime. The distribution of elastic impulses over their energies
in processes of deformation and brittle fracture of various materials and rocks
was widely studied under laboratory conditions and in in situ experiments
(deformations of rock masses in mines)
[Mogi, 1962, 1967;
Scholz, 1968a, 1968b;
Vinogradov, 1957, 1959, 1963,
1964;
Zhurkov et al., 1977].
As was shown in a number of studies, this distribution is similar in shape to the
distribution of earthquakes over energies. This inference served as an argument for
the principle of fracture similarity at various scale levels
[Kostrov, 1975;
Myachkin, 1978;
Myachkin et al., 1975]
and provided a basis for the study of the
earthquake preparation process under laboratory conditions and in mines
[Vinogradov, 1957, 1963].
The validity of this approach was confirmed in
[Ponomarev et al., 1997;
Smirnov et al., 1995a, 1995b,
1995c;
Zavyalov and Sobolev, 1988].
Acknowledging the fundamental nature of the recurrence law, which was initially
inferred experimentally, researchers have repeatedly attempted to derive it theoretically
[Gurevich et al., 1960;
Hausner, 1955;
Mogi, 1962;
Petrov, 1981].
In all these papers, the authors postulated certain initial presumptions and
obtained dependences of the number of earthquakes on their magnitude that were
similar to the recurrence law. The theoretical recurrence plot slope in these
relations was a constant value.
Pod'yapolsky [1968] and Kuznetsova [1976]
arrived at a conclusion, important from the standpoint of prediction studies:
the value
g is not constant but depends on material properties
and conditions
of a loading process. This implies that variations in
g with time observed in
laboratory experiments and in situ observations yield evidence on the state
of
material in a fracture source. This idea was further developed and confirmed by
Meredith et al. [1990].
Laboratory studies of rock fracture and observations in mines have shown that
the macrofracture preparation process is characterized by regular temporal
variations in the ratio of the numbers of strong shocks to weak ones, which is
equivalent to variations in the slope of the plot showing the distribution of
acoustic impulses over energies. Studies in mines have shown that, as compared
with quiescent periods, the ratio of the numbers of strong pulses to weak ones
increases by three to seven times 15-18 hours to 1 month before a rockburst,
after which this ratio drops
[Cai et al., 1988;
Ponomarev et al., 1997;
Scholz, 1968a, 1968b;
Smirnov et al., 1995a, 1995b,
1995c;
Vinogradov, 1957, 1963, 1964].
Similar variations in
g were also observed in detailed studies of seismic
regimes in various seismically active regions of the world
[Adams, 1976;
Katon et al., 1981;
Mamadaliev, 1964;
Mikhailova, 1980a;
Van Wormer et al., 1976;
Zavyalov, 2003b;
Zavyalov and Sobolev, 1980;
Zhang and Fu, 1981].
Thus, there is every reason to suggest that a parameter indicating a forthcoming
macrofracture is an anomalous variation in the recurrence plot slope whose value
first anomalously increases and then drops until the onset of macrofracture
(rockburst or earthquake). As regards the physics of the macrofracture process,
the
g increase is associated with the formation of
small fractures (weak
earthquakes) that are much more numerous compared to the number of large
fractures (moderate earthquakes) in the preparation region of a forthcoming
strong earthquake. When the concentration of small fractures reaches a critical
value, processes of interaction between small cracks and their coalescence
become active; as a result, the number of large fractures increases relative to
small ones and the value of
g decreases until the onset moment of the major
rupture (a strong earthquake).
Using the maximum likelihood method, the value
g is calculated by the formula
[Gusev, 1974]
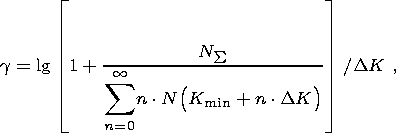 | (3) |
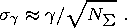 | (4) |
Here
NS is the total number of earthquakes
in the range of energy
classes from
Kmin to
Kmax (the sample size);
N(Kmin + n DK) is the number of earthquakes of the energy
class
Kmin+n
DK) is the number of earthquakes of the energy
class
Kmin+n DK,
n = 0, 1, 2,...,
and
DK is the unity of the energy class range.
DK,
n = 0, 1, 2,...,
and
DK is the unity of the energy class range.
Using the parameter
g for prediction analysis of strong earthquakes,
we
represented its temporal variations in terms of a dimensionless quantity
xg
characterizing the statistical significance of deviations of current values of
the parameter
g from its long-term values normalized to the
rms error of
their determination (7).
The following formal rule was used for the identification of precursory
anomalies in the parameter
xg
[Zavyalov, 1984b].
The criterion of the anomaly onset is the increment in
xg
above a certain alarm level
x alg
chosen empirically from a retrospective examination of available data.
Anomalous values of
xg
reach a maximum followed by their decrease, sometimes to negative values.
The termination moment of the
xg
anomaly is defined by its transition through a
level
x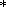 g determined also empirically from a new increase
in the
xg
value. The time from the onset of he anomaly to its termination is regarded as
its period
Tan.
g determined also empirically from a new increase
in the
xg
value. The time from the onset of he anomaly to its termination is regarded as
its period
Tan.
The anomaly is considered as realized if a single earthquake of the predicted
energy class
Kpr or a group of such earthquakes occurs within the anomaly
period
Tan in the seismically active subregion (cell) under study
DSi.
In this case, the time from the anomaly onset to the moment of the seismic event
is
the expectation time of this event
Texp (evidently,
Texp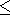 Tan ).
If no strong earthquake occurs during the time
Tan, the anomaly is considered as
false and its duration is the false alarm time
Tf.a..
Tan ).
If no strong earthquake occurs during the time
Tan, the anomaly is considered as
false and its duration is the false alarm time
Tf.a..
The above model describing the behavior of the precursor
xg
is consistent with
results of laboratory experiments on fracture of rocks and model materials, as
well as with the AUF model concepts.
The following formal scheme implementing the use of the parameter
xg
for
prediction of strong earthquakes was proposed in
[Zavyalov, 1984b].
(i) Spatial distributions of the parameter
xg
are calculated, at
step
Dt, for preliminarily chosen cell sizes
DSi and widths
of the current ( DTc ) and long-term ( DTl ) moving time windows.
(ii) As soon as values
xg xg
al appear in a subregion
DSi, the expectation period
of a strong earthquake is declared in this subregion.
xg
al appear in a subregion
DSi, the expectation period
of a strong earthquake is declared in this subregion.
(iii) The expectation state is preserved for the time period
Texp+|sT|
determined empirically from retrospective analysis of available data and can be terminated
before the expiration of the expectation period in the following two cases:
(a) after the occurrence time of a strong earthquake in the subregion considered;
(b) with a new increase in the value
xg
above the level
x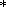 g=+1,
following the period of its decrease.
g=+1,
following the period of its decrease.
In the first case, the time from the anomaly onset to the
strong earthquake
occurrence is the expectation time
Texp. The time interval in the second case
is the false alarm period
Tf.a.. A typical dependence of
xg
versus
time before a strong earthquake is shown in Figure 1b.
Number of events per unit time N.
A very important characteristic of rock
fracture under laboratory conditions and of the seismic regime in a seismically
active region is the number of acoustic pulses (earthquakes) recorded per unit time.
Vinogradov [1980]
noted that the time distribution of elastic impulses
characterizes the evolution of fracture processes in the study volume depending
on the strain rate, material properties and, primarily, heterogeneity of the medium.
Sobolev [1993]
pointed out that the acoustic emission induced by deformation of rock samples reflects
the fracturing process and can be considered, with some reservations, as an analogue
of the seismic process in the Earth.
A review of published data on the generation of acoustic (seismic) impulses
indicates that the study of the temporal distribution of elastic impulses
(background earthquakes in seismically active regions) is beneficial to
prediction of a macrofracture (an earthquake)
[Atkinson, 1981;
Borovik, 1977;
Evisson, 1977;
Fedotov et al., 1969;
Inouye, 1965;
Kerr, 1979;
Mikhailova, 1980a;
Mogi, 1962, 1968a, 1968b;
Nersesov et al., 1976, 1979;
Rummel and Sobolev, 1983;
Shamina, 1956;
Teitelbaum and Ponomarev, 1980;
Tomashevskaya and Khamidullin, 1972;
Vinogradov, 1957, 1963;
Vinogradov et al., 1975;
Zavyalov and Sobolev, 1980, 1988].
Strong earthquakes can be preceded by
periods of both attenuation of seismic activity (a decrease in the number of
background earthquakes) and its enhancement (an increase in the number of
background earthquakes). In some cases, both types of the premonitory variations
separated in time can be observed in the same region. These schemes are
qualitatively accounted for in terms of the AUF model of earthquake preparation.
The average number of earthquakes per unit time in the range of energy classes
from
Kmin to
Kmax and its rms error are determined by the formulas
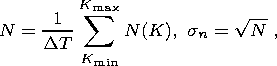 | (5) |
where
N(K) is the number of earthquakes of the energy class
K, and
DT is the length of the observation period
(time window width). A dimensionless parameter
xn defined in the same way as
the parameter
xg
is taken as the measure
of statistical significance.
If seismic quiescence is sought, the anomaly onset time is determined from
the
appearance of values
xn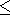 xnq al, where
xnq al is
an empirically chosen alarm level. If seismicity activity is sought,
the anomaly onset time is determined from the appearance of values
xn
xnq al, where
xnq al is
an empirically chosen alarm level. If seismicity activity is sought,
the anomaly onset time is determined from the appearance of values
xn xna al,
where
xna al is an empirically
chosen alarm level. The rule for
the anomaly identification from the parameter
xn is similar to the rule described
above
for the parameter
xg
and complies with the generally acknowledged idea that
an earthquake is preceded by either seismic quiescence or a foreshock activation
period.
xna al,
where
xna al is an empirically
chosen alarm level. The rule for
the anomaly identification from the parameter
xn is similar to the rule described
above
for the parameter
xg
and complies with the generally acknowledged idea that
an earthquake is preceded by either seismic quiescence or a foreshock activation
period.
An anomaly is considered false if no earthquakes of predicted energy class
Kpr occurs over the time
Texp+|sT|
in the seismically
active volume considered. In this case, the anomaly duration is the false alarm period.
On the other hand, if an earthquake or a group of earthquakes of the predicted energy
class occurs in the time interval
Texp+|sT|,
the time from the anomaly onset to the earthquake
occurrence is regarded as the expectation period for the given seismic event
and, with the end of this period the anomaly is regarded as realized.
The scheme of using the parameter
xn for prediction of strong
earthquakes is
similar to that proposed for the parameter
xg.
A typical example of the
dependence of
xn versus time before a strong
earthquake is given in Figure 1c.
Released seismic energy
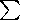 E2/3.
E2/3.
The parameter
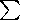 E2/3
was proposed and tested by
Keilis-Borok [1959] for strong ( M>7 ) earthquakes. The physical
meaning of this parameter consists in rapid accumulation of dynamic rupture areas
producing earthquakes smaller than a given energy class
K0 in the preparation
region of a strong earthquake
[Sadovsky and Pisarenko, 1983].
Keilis-Borok and Malinovskaya [1966]
noted the following important relation: a strong earthquake
occurs when the sum of the weak earthquake rupture areas becomes equal to the
area of the main rupture. According to the AUF model of earthquake preparation,
the dependence
E(t)=
E2/3
was proposed and tested by
Keilis-Borok [1959] for strong ( M>7 ) earthquakes. The physical
meaning of this parameter consists in rapid accumulation of dynamic rupture areas
producing earthquakes smaller than a given energy class
K0 in the preparation
region of a strong earthquake
[Sadovsky and Pisarenko, 1983].
Keilis-Borok and Malinovskaya [1966]
noted the following important relation: a strong earthquake
occurs when the sum of the weak earthquake rupture areas becomes equal to the
area of the main rupture. According to the AUF model of earthquake preparation,
the dependence
E(t)=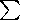 E2/3
plotted for weak earthquakes over time intervals
DT much shorter than the preparation time
of the main rupture should have
a baylike shape in the fracturing process
[Myachkin, 1978;
Myachkin et al., 1975].
Myachkin et al. [1975] emphasized that such behavior
of a precursor
is only possible immediately in the zone of the avalanche-like growth of fractures
and
the formation of the future main rupture, which is important for predicting the
place of the forthcoming shock.
E2/3
plotted for weak earthquakes over time intervals
DT much shorter than the preparation time
of the main rupture should have
a baylike shape in the fracturing process
[Myachkin, 1978;
Myachkin et al., 1975].
Myachkin et al. [1975] emphasized that such behavior
of a precursor
is only possible immediately in the zone of the avalanche-like growth of fractures
and
the formation of the future main rupture, which is important for predicting the
place of the forthcoming shock.
The parameter
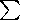 E2/3
is determined by the formula
E2/3
is determined by the formula
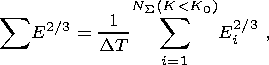 | (6) |
where
NS(K < K0)
is the number of earthquakes of energy classes
smaller than the given level
K0.
Similar to the cases of the recurrence plot slope and the number of earthquakes
considered above, the dimensionless parameter
xe (7) is accepted as the
measure of statistical significance. The released seismic energy, similar to the
number of earthquakes, is used in two modifications: as energy quiescence
(the
parameter
xeq ) and as activation of
seismic energy release ( xea ).
The scheme of the identification of precursory anomalies from the parameter
xe and its application to prediction
of strong earthquakes is similar to those described
above for
xg
and
xn. A typical dependence of
xe versus time
before a strong earthquake is shown in Figure 1d.
The above can be summarized as follows. A short review of earthquake preparation
models has revealed their advantages and drawbacks setting limits to their
possible applications to the interpretation of observed experimental data and
the development of earthquake prediction methods. A general characteristic of
these models consists in the fact that they are qualitative and useless for a
quantitative description of the fracture preparation process in heterogeneous
media including deep rocks of the Earth. An exception is the consolidation model
allowing one to gain numerical constraints on the strain field and related precursors.
The preparation models, describing the behavior of prognostic parameters at
various stages of the earthquake preparation process, provided a physical basis
for the medium-term earthquake prediction from a complex of prognostic
parameters and pointed out requirements to the relevant choice of precursors.
Prognostic parameters meeting these requirements and included for their use in
the algorithm of mapping expected earthquakes (MEE) were described.
Based on physical principles and the experience of retrospective analysis using
the criteria described above, we developed models describing the behavior of
prognostic parameters during preparation of earthquakes and proposed algorithms
for their use in prediction practice.
4. Prognostic Algorithm of Mapping Expected Earthquakes
(MEE)
The MEE algorithm is a complex of procedures designed for estimating the
conditional probability of strong earthquake occurrence
P(D1| K) in
a time period [t0, t0+DTMEE] in rectangular cells of given
sizes that form a grid covering the seismically active region studied.
A map of expected earthquakes is meant as the
set of conditional probability values
P(D1| K) calculated for all
spatial cells in the given region and represented in the form of contours.
The value
DTMEE denotes the serviceable
time of the map of
expected earthquakes (EE) during which a strong earthquake can occur.
We constructed the MEE algorithm using the Bayes approach as the most widespread
and simple technique. It is based on the use of probabilities that certain
indicators (prognostic parameters
Ki ) assume values complying with a diagnosis
(hypothesis)
Dj.
Main principles of the MEE algorithm construction.
The MEE algorithm of
earthquake prediction is based on the principle of spatial-temporal scanning of
a catalog of earthquakes in the seismically active region to be analyzed. The
region is covered by a rectangular grid of
DX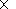 DY cells,
and values of various prognostic parameters are calculated for each cell
in a moving time window of a width
DT at a step
Dt.
Neighboring cells are either independent or can partly overlap each other
[Sobolev et al., 1990, 1991;
Zavyalov et al., 1995;
Zavyalov, 2002].
Overlapping of neighboring cells can be used to partly estimate
uncertainties of epicenter determinations.
DY cells,
and values of various prognostic parameters are calculated for each cell
in a moving time window of a width
DT at a step
Dt.
Neighboring cells are either independent or can partly overlap each other
[Sobolev et al., 1990, 1991;
Zavyalov et al., 1995;
Zavyalov, 2002].
Overlapping of neighboring cells can be used to partly estimate
uncertainties of epicenter determinations.
The main database used in the MEE algorithm is a catalog of earthquakes in the
seismically active region under study; this catalog should be representative and
homogeneous for earthquakes of energy classes
K K0 (M
K0 (M M0).
M0).
Two types of diagnoses are possible in the case of earthquake prediction:
occurrence (diagnosis
D1 ) or nonoccurrence ( D2 ) of a strong earthquake in
the spatial cell under consideration. The probabilities of these diagnoses
P(D1) and
P(D2) are calculated using the earthquake catalog, without
regard for any
prognostic parameters; the calculated values (Table 1) are unconditional probabilities (UPs).
The MEE algorithm uses two groups of prognostic parameters, quasi-stationary and
dynamic. The first group includes geological and geophysical parameters that do
not vary or vary weakly during an observation period and the strong earthquake
preparation time, are physically related to the occurrence of earthquakes, and
can be mapped throughout the observation area (see Chapter 3). The quasi-stationary
parameters are used for differentiating the observation area
according to the level of unconditional probability of strong earthquake
occurrence
P(D1). Experience of MEE applications in various seismically
active
regions of the world showed that the incorporation of quasi-stationary
indicators the unconditional probability
P(D1) by a factor of 1.5-2 in cells
where they are observed and decreases it by the same factor in cells where they
are not observed. The following quasi-stationary parameters can be utilized: the
number of tectonic faults of a given rank in a cell, the number of fault
intersections in a cell, the velocity gradient of recent movements, gravity anomalies,
etc.
Dynamic criteria include geophysical parameters estimated from regular
seismological observations, as well as observations of other geophysical fields
that have clear physical meaning and are related to the preparation of strong
earthquakes. The variation period of the dynamic parameters is much shorter than
the observation period and the preparation time of a strong earthquake. A
necessary condition for using a given dynamic criterion in the MEE algorithm is
the possibility of its mapping (see the paragraph "Choice of Precursors'').
No limitations are imposed on the number of quasi-stationary and dynamic
prognostic parameters used in the MEE algorithm and, in this sense, the
algorithm is open.
In regular observations of geophysical parameters, a researcher is often
interested not in the values of these parameters but in their statistically
significant deviations from their long-term values. The statistical significance
of the observed deviations of prognostic parameters is particularly important in
establishing their relation to subsequent catastrophic natural phenomena. This
approach is used in the MEE algorithm.
|
|
Figure 2
|
All dynamic prognostic parameters
Ki, with the exception of the seismogenic
fault concentration
Ksf having a cumulative nature and being a threshold
quantity, are represented as spatial-temporal distributions of anomalous
deviations from a corresponding long-term (background) level that are normalized
to the rms error of its determination. The parameter
xKi taken
as a measure of
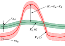
statistical significance is defined as follows (Figure 2)
[Zavyalov, 1984a, 1984b]:
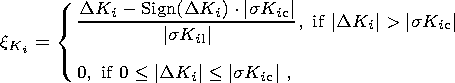 | (7) |
where
DKi=Ki
c-Ki l;
Ki c and
sKi c are the current
value
of the prognostic parameter and its standard deviation in the moving time window
DTc calculated from pertinent
formulas (see Chapter 3); and
Ki l and
sKi l are
long-term (background) values calculated in the moving time window
DTl > DT
c.
Each dynamic parameter has retrospective statistical estimates obtained for
chosen alarm levels; the most important of these estimates are the detection
probability
P(Ki|D1), i.e. the probability
of occurrence of a strong earthquake
after anomalous values of the parameter
Ki were recorded; the false alarm
probability
P(Ki|D2), i.e. the potential of
nonoccurrence of a strong earthquake
after anomalous values of
Ki were recorded; the average time of expectation of
a strong earthquake
Texpi; and the average expectation area
Sexpi.
The expectation time
Texpi is defined as the time from the initial
moment of
recording
Ki values that exceed a given alarm level (anomalous values)
to the
occurrence moment of a strong earthquake. If no earthquake occurs, this time is
considered as the false alarm time
Tif.a..
The expectation area
Siexp of a strong earthquake in relation to
the
prognostic parameter
Ki is the sum of areas of
DX DY cells
in which the expectation state is declared, i.e.
Ki values in these cells are
anomalous, exceeding the given alarm level. If no strong earthquake occurs in
these cells, their total area is considered as the false alarm area
Sif.a..
DY cells
in which the expectation state is declared, i.e.
Ki values in these cells are
anomalous, exceeding the given alarm level. If no strong earthquake occurs in
these cells, their total area is considered as the false alarm area
Sif.a..
Expressions used for the determination of retrospective statistical
characteristics are presented in Table 1.
The alarm level for each prognostic parameter is chosen through expert analysis
based on the set of retrospective statistical estimates and other a priori
information.
The detection probability
P(Ki| D1) is defined as the ratio
of the number
of strong earthquakes
Npr preceded by an anomaly of the parameter
Ki (predicted strong earthquakes)
to the total number of strong earthquakes
Ntotal that occurred during the observation period in the observation
area
[Zavyalov et al., 1995].
In turn, the false alarm probability
P(Ki| D2) is the ratio of the
false alarm area
to the observation area (Table 1).
The conditional probability of strong earthquake occurrence
P(D1| K) determined
from a complex of prognostic parameters in each spatial cell
DSMEE is
calculated by the Bayesian formula; given two diagnoses, this formula has the form
P(D1 K) =
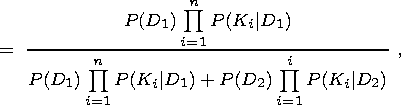 | (8) |
In the absence of anomalous values of the prognostic parameter
Ki, the
probabilities
P(Ki | D1) and
P(Ki | D2) in (8) are replaced
by the probabilities
1-P(Ki | D1) and
1-P(Ki | D2).
We assume that all parameters used here are simple, i.e.
the presence of anomalous values of
Ki in the cell under consideration is
coded as "1'' and their absence, as "0''. If quasi-stationary prognostic
parameters
K i are used,
the unconditional probabilities
P(D1) and
P(D2) in grid cells are replaced by the stationary conditional
probabilities
P(K
i are used,
the unconditional probabilities
P(D1) and
P(D2) in grid cells are replaced by the stationary conditional
probabilities
P(K i
| D1) and
P(K
i
| D1) and
P(K i
| D2).
Values of the latter are calculated by formula (8).
i
| D2).
Values of the latter are calculated by formula (8).
The set of conditional probabilities
P(D1 | K) for all spatial cells represented in
the form of contours was called the map of expected earthquakes for the time
period
[t0, t0+DT
MEE], where
DTMEE is the MEE
serviceability time (Table 1). Occurrence of a strong earthquake in this time interval
is assumed to be equiprobable.
The area of MEE alarm zones
Sjexp is the total area of cells in which the
conditional probability of strong earthquake occurrence
P(D1 | K) exceeds a given
level. The average area of alarm zones
Sal with a given level of
conditional probability of strong earthquake occurrence is determined by the expression
given in Table 1.
In order to select prognostic criteria for their use in the calculation of the
conditional probability
P(D1 | K), we estimated their prognostic effectiveness
in time ( Jt ) and in area ( Js ). The prognostic effectiveness of each criterion
was estimated retrospectively, as the ratio of the average flow density of
strong earthquakes over the alarm time (or over the alarm area) to their average
density over the observation time (or over the observation area) (Table 1)
[Fedotov et al., 1976].
Here,
Npr and
Ntotal are, respectively, the number of predicted strong earthquakes
and the total
number of earthquakes that occurred over the observation time
Tobs in the observation area
Sobs;
Texp.total is the total time
of expectation (alarm); and
Sexp.total. is the total area of
expectation (alarm). This definition implies that
J = 1 if a successful
prediction was random (the prognostic criterion is unrelated to the
preparation of a strong earthquake), when the densities of earthquakes to be
predicted in the alarm and observation periods (areas) coincide. The larger the
deviation of the effectiveness parameter from 1, the more effective the
prognostic criterion in use. Prognostic criteria with an effectiveness of less
than 1.2 were rejected from MEE calculations.
The prognostic effectiveness of the MEE algorithm as a whole,
JMEE (Table 1),
is defined as the ratio of the flow density of strong earthquakes in the
average alarm area to its value in the observation area at a given level of
seismic activity (commonly no less than one earthquake per year).
5. Testing of the Prognostic MEE Algorithm in Various
Seismically Active Regions
from 1985 through 2002
Initially, the MEE algorithm was developed and tested for the Caucasus
[Sobolev et al., 1990, 1991;
Zavyalov, 1993].
Afterward it was tested in seismically active regions of Kamchatka
[Zavyalov and Levina, 1993];
Turkmenistan [Zavyalov and Orlov, 1993];
Kyrgyzstan, southern California, northeastern and southwestern China
[Zavyalov and Zhang, 1993];
Greece [Zavyalov, 1994, 2003a;
Sobolev et al., 1999];
and western Turkey [Zavyalov, 2003b].
In all of these regions differing in their seismotectonic conditions,
a unified approach was applied to the distribution of prognostic parameters,
estimation of their retrospective statistical characteristics, choice of optimal
alarm levels and the strength of predicted earthquakes, and so on. In doing so,
we proceeded from the assumption on the similarity between earthquake preparation
processes in seismotectonically different regions based on the concept of
self-similarity of geodynamic processes
[Sadovsky, 1986].
This approach proved effective in accumulating, over
a relatively short time interval, statistically rather representative data
sufficient in order to draw reliable conclusions concerning prognostic
capabilities of the MEE algorithm.
The main database of the MEE algorithm was compiled from regional earthquake
catalogs, each including a few thousand events and covered a period of a few
tens of years. Depending on a region, earthquakes with
Kpr 12.5 ( Mpr
12.5 ( Mpr 5.5 )
were objects of prediction analysis. Stationary prognostic parameters were used
in some seismically active regions.
5.5 )
were objects of prediction analysis. Stationary prognostic parameters were used
in some seismically active regions.
Comparison of optimal alarm levels chosen in various seismically active regions
showed that, for each precursory parameter, these levels vary weakly from region
to region. This indicates the stability of the algorithm parameters in relation
to various seismically active regions differing in geological and tectonic
conditions. For the majority of precursors in all regions studied, the detection
probability estimated from each precursor is a few times lower than the
conditional probability
P(D1 | K) amounting to 70% (90% if a complex of
the
precursors is used). Usually, the detection probability obtained from an
individual precursor is 1.5-2 times higher than the unconditional probability
P(D1) but can occasionally be even lower than the latter.
An exception is the
parameter
Ksf yielding a detection probability higher than the unconditional
probability by a factor of 2.5 and more. The conditional probabilities of strong
earthquake occurrence
P(D1 | K) = 70% and 90% were chosen as alarm levels
for
the analysis of a complex of prognostic parameters.
The prognostic effectiveness of all parameters varies from region to region. The
most effective precursor in all regions is the parameter
Ksf. Its prognostic
effectiveness averages
Jt = 4.96 2.39. A parameter
next in effectiveness is
Nact - Jt = 3.96
2.39. A parameter
next in effectiveness is
Nact - Jt = 3.96 1.66. Less effective are the quiescence in
relation to the number of events ( Jt = 3.19
1.66. Less effective are the quiescence in
relation to the number of events ( Jt = 3.19 0.94 ) and
the recurrence plot
slope ( Jt = 2.24
0.94 ) and
the recurrence plot
slope ( Jt = 2.24 0.73 ). The
two parameters related to the seismic energy
release proved least effective. The parameter
Eq (quiescence in relation to
the energy release) had an overly low effectiveness ( J
0.73 ). The
two parameters related to the seismic energy
release proved least effective. The parameter
Eq (quiescence in relation to
the energy release) had an overly low effectiveness ( J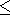 1 ) in several regions
and was not used there.
1 ) in several regions
and was not used there.
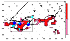
|
|
Figure 3
|
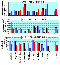
|
|
Figure 4
|
As an example, the Kamchatka EE map is shown in Figure 3.
Analysis of a set of EE maps in the study regions have shown that, using the
value
P(D1 | K) = 70% as an alarm level (exceeding the
unconditional probability in
these regions by about three times), the MEE algorithm effectiveness
JMEE ranges from 1.29 (the Caucasus) to 4.40 (S. California),
whereas
JMEE varies
within the range 2.02-5.84 with the level
P(D1 | K) = 90%. The average value of the
MEE algorithm effectiveness
JMEE amounts to 2.45
 0.94 for the level
P(D1 | K) = 70% and 3.14
0.94 for the level
P(D1 | K) = 70% and 3.14
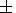 1.23 for
P(D1 | K) = 90%. In zones
with
P(D1 | K)
1.23 for
P(D1 | K) = 90%. In zones
with
P(D1 | K) 70%, 48%
(Greece) to 80% (SW China) of the predicted earthquakes
occurred over the serviceability time of the
corresponding EE maps (a few years). The average area of the corresponding alarm
zones was 12.7% to 58.1% of the observation area with a seismicity level of at
least one earthquake per year (commonly, 1.5-2 times smaller than the total area
of observations). These data are plotted in Figure 4.
70%, 48%
(Greece) to 80% (SW China) of the predicted earthquakes
occurred over the serviceability time of the
corresponding EE maps (a few years). The average area of the corresponding alarm
zones was 12.7% to 58.1% of the observation area with a seismicity level of at
least one earthquake per year (commonly, 1.5-2 times smaller than the total area
of observations). These data are plotted in Figure 4.
Results of the long-term testing of the MEE algorithm in various seismically
active regions showed that its average prognostic effectiveness is 2.5 times
higher than the random guessing value. On average, 68% of the predicted
earthquakes occurred in zones with
P(D1 | K) 70%, and
the average area
of alarm zones amounted there to 30% of the area with a seismicity level of
at least one earthquake per year. These data yield an idea of the real potential
prognostic capabilities of the MEE algorithm.
70%, and
the average area
of alarm zones amounted there to 30% of the area with a seismicity level of
at least one earthquake per year. These data yield an idea of the real potential
prognostic capabilities of the MEE algorithm.
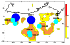
|
|
Figure 5
|
Figure 3,
illustrating a rather typical example, shows that several large
zones of high values of
P(D1 | K) exist in seismically active regions.
Detailed EE maps, with smaller sizes of spatial cells, were constructed for a
southern seismically active 360
 240-km region of Kamchatka from Cape
Lopatka to Cape Shipunski (the rectangular area in Figure 3). The cell areas
amounted to 30
240-km region of Kamchatka from Cape
Lopatka to Cape Shipunski (the rectangular area in Figure 3). The cell areas
amounted to 30
 30 km for calculating the parameter
Ksf and
60
30 km for calculating the parameter
Ksf and
60
 60 km for the remaining precursory parameters.
One of the EE maps
of this region is presented in Figure 5.
60 km for the remaining precursory parameters.
One of the EE maps
of this region is presented in Figure 5.
Comparison of retrospective statistical characteristics for the whole Kamchatka
Peninsula and its southern part reveals a decrease in the prognostic
effectiveness of all precursory parameters in the whole Kamchatka region, which
is related to an increase in the false alarm probability. The
Ksf effectiveness decrease is particularly pronounced (by more
than two times).
However, the alarm level and the average expectation time changed
insignificantly, indicating that the algorithm parameters are stable with
respect to variations in the spatial cell sizes. Analysis of the whole series of
maps for southern Kamchatka leads to the conclusion that the prognostic
effectiveness of the EE map series for southern Kamchatka is more than two times
higher than its value for the whole Kamchatka region. This appears to be
primarily related to a decrease in the alarm area in this part of the region.

|
|
Figure 6
|
In order to examine the effectiveness of the MEE algorithm as a function of the
energy class of predicted earthquakes and the depth range of the seismically
active layer, we calculated EE map series for Kamchatka with the following
parameters:
Kpr 14.5,
H = 0-100 km;
Kpr
14.5,
H = 0-100 km;
Kpr 13.5,
H = 0-50 km (Figure 6a); and
Kpr
13.5,
H = 0-50 km (Figure 6a); and
Kpr 13.5,
H = 25-75 km (Figure 6b).
Retrospective statistical characteristics in these cases also display a low
sensitivity of the algorithm parameters to variations in earthquake parameters
involved in the calculations. Analysis of the EE maps constructed in these three
variants shows that their prognostic effectiveness is higher compared to the basic
variant ( Kpr
13.5,
H = 25-75 km (Figure 6b).
Retrospective statistical characteristics in these cases also display a low
sensitivity of the algorithm parameters to variations in earthquake parameters
involved in the calculations. Analysis of the EE maps constructed in these three
variants shows that their prognostic effectiveness is higher compared to the basic
variant ( Kpr 13.5,
H = 0-100 km). A high efficiency of the
Kpr
13.5,
H = 0-100 km). A high efficiency of the
Kpr 14.5 earthquake prediction
( JMEE = 6.5 with
P(D1 | K) = 70%) is due to a
significant decrease in the alarm area. Because of small statistics of
Kpr
14.5 earthquake prediction
( JMEE = 6.5 with
P(D1 | K) = 70%) is due to a
significant decrease in the alarm area. Because of small statistics of
Kpr 15.5 earthquakes (only three
such events occurred over the period from 1962 through 2000),
this energy range of predicted earthquakes was not analyzed.
15.5 earthquakes (only three
such events occurred over the period from 1962 through 2000),
this energy range of predicted earthquakes was not analyzed.
The maps presented in Figures 6a and 6b show that the epicentral positions
of the main shock of the Kronotski, December 5, 1997 earthquake ( K = 15.5,
H = 10 km) and several of its aftershocks coincide with the zone of
P(D1 | K) 70%,
whereas the larger part of the aftershock area is characterized by values
P(D1 | K)
70%,
whereas the larger part of the aftershock area is characterized by values
P(D1 | K) 50%. On
the other hand, as seen from Figure 6b showing the distribution of
the conditional probability
P(D1 | K) for the depths
H = 25-75 km, only an
insignificant part of the aftershock zone has its values in the range
50%
50%. On
the other hand, as seen from Figure 6b showing the distribution of
the conditional probability
P(D1 | K) for the depths
H = 25-75 km, only an
insignificant part of the aftershock zone has its values in the range
50% 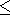 P(D1 | K)
P(D1 | K) 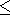 70%. Such a distribution pattern implies that the preparation
process
of the Kronotski earthquake developed mostly in the depth range
H = 0-25 km,
which agrees with data of instrumental determinations of its hypocentral depth.
Apparently, the MEE algorithm is capable of predicting the source depth of a
future earthquake.
70%. Such a distribution pattern implies that the preparation
process
of the Kronotski earthquake developed mostly in the depth range
H = 0-25 km,
which agrees with data of instrumental determinations of its hypocentral depth.
Apparently, the MEE algorithm is capable of predicting the source depth of a
future earthquake.
Calculations of EE maps for western Turkey with the cell sizes
DSMEE = 50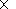 50 km,
75
50 km,
75
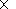 75 km and 100
75 km and 100
 100 km provided constraints on the effect
of the averaging cell
size on the prognostic properties of the MEE algorithm. The MEE algorithm proved
most effective with the cell size
DSMEE = 75
100 km provided constraints on the effect
of the averaging cell
size on the prognostic properties of the MEE algorithm. The MEE algorithm proved
most effective with the cell size
DSMEE = 75 75 km
( JMEE = 3.29 ), whereas its effectiveness was lowest in the
case of
DSMEE = 50
75 km
( JMEE = 3.29 ), whereas its effectiveness was lowest in the
case of
DSMEE = 50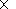 50 km ( JMEE = 1.19 ). We
may suggest that calculations with various sizes of averaging cells and
comparison of their results with estimated sizes of the earthquake source and
preparation areas as a function of the earthquake magnitude will be helpful for
more accurate adjustment of the MEE algorithm to earthquake prediction in a
given range of magnitudes.
50 km ( JMEE = 1.19 ). We
may suggest that calculations with various sizes of averaging cells and
comparison of their results with estimated sizes of the earthquake source and
preparation areas as a function of the earthquake magnitude will be helpful for
more accurate adjustment of the MEE algorithm to earthquake prediction in a
given range of magnitudes.
The long-term testing of the MEE algorithm has revealed some
of its drawbacks.
The most significant of the latter is as follows. As mentioned above, EE maps
usually exhibit zones of high conditional probabilities of the occurrence of a
strong earthquake. Several alarm zones are also observable even in the EE maps
constructed for the Cape Lopatka-Cape Shipunski in Kamchatka (Figure 5). This
implies that, using solely the prognostic capabilities of the MEE algorithm and
related individual precursors, one cannot localize the zone of a future strong
earthquake. This can be done by invoking, first, shorter-term precursors
(compared to precursors involved in the MEE algorithm procedure) and, second,
precursors of the nonseismological type (e.g. the water level in wells, radon
concentration, electromagnetic emission, and so on). Therefore, the MEE
algorithm can be recommended, on the one hand, as a means complementing
observations of other precursors in inferred zones of high conditional
probabilities (more than 70%) and, on the other hand, for taking preventive
measures to mitigate the possible economic and social damage of a future strong
earthquake.
In the last decade, the feasibility of earthquake prediction has been widely discussed
[Deshcherevsky et al., 2003;
Geller, 1997;
Geller et al., 1997;
Kagan, 1997;
Leary, 1997;
Sobolev, 1999;
Wyss, 1997].
In this discussion, both authors denying or doubting the earthquake prediction feasibility
[Geller, 1997;
Geller et al., 1997;
Kagan, 1997;
Leary, 1997]
and authors adhering to an opposite point of view
[Sobolev, 1999;
Wyss, 1997]
invoke rather weighty arguments in favor of their ideas, up to a change of a research
paradigm in the field of earthquake prediction
[Deshcherevsky et al., 2003].
As regards the question of whether earthquakes can be predicted, the author of the
present
paper believes that this question can be answered in two possible ways.
(i) Since our knowledge of the earthquake preparation process is still incomplete
and inadequate, earthquakes cannot be predicted. One should wait until the time
when this knowledge becomes complete and only then start predicting real
earthquakes. (ii) Based on the presently existing knowledge of the earthquake
preparation process and known precursors and using available prediction
algorithms, one should try to predict earthquakes, gaining in this way new
knowledge and accumulating the prediction experience. Undoubtedly, such
predictions should be probabilistic and their confidence levels should be
estimated.
Here, we arrive at the following conclusion: in order to accumulate experience
within the framework of the Code of earthquake prediction ethics
[Sobolev et al., 1994],
we can, in addition to the study of individual precursors, carry
out tentative systematic scientific prediction of strong earthquakes on a real
time scale, using available algorithms and precursors
[ Sadovsky, 1986;
Sobolev et al., 1990, 1991].
Thus, long-term testing of the MEE algorithm in various seismically active
regions has shown that the average prognostic effectiveness of the algorithm
JMEE is 2.5 times higher than in the case of random guessing.
In this respect, we should note that about 68% of earthquakes involved in
the prediction occurred in zones of the conditional probability
P(D1 | K) 70%, and
the average area of alarm zones amounted to 30%
of the area where the seismicity level was one earthquake per year or more.
These data are evidence of the real prognostic potential of the algorithm.
70%, and
the average area of alarm zones amounted to 30%
of the area where the seismicity level was one earthquake per year or more.
These data are evidence of the real prognostic potential of the algorithm.
The most effective prognostic criterion used in the MEE algorithm is the density
of seismogenic faults
Ksf. Its prognostic effectiveness in five
of nine tested seismically active regions was
J 4.
4.
The case study of the Ust-Kamchatka, December 5, 1997 earthquake ( K = 15.5) has
demonstrated the MEE algorithm potentialities in relation to the source depth
prediction of a future strong earthquake. The study in the Kamchatka region has
also shown that the prognostic effectiveness of the MEE algorithm increases when
the algorithm is applied to prediction of the strongest earthquakes.
The case study of western Turkey has shown that calculations with various sizes
of averaging cells and comparison of their results with estimated sizes of the
earthquake source and preparation areas as a function of the earthquake
magnitude is helpful for more accurate adjustment of the MEE algorithm to
prediction of earthquakes in a given range of magnitudes.
The long-term testing results indicate that the MEE algorithm can be
recommended, on the one hand, as a means complementing observations of other
precursors in inferred zones of high conditional probabilities (more than 70%)
and, on the other hand, for taking preventive measures to mitigate the possible
economic and social damage of a future strong earthquake.
6. Application of the MEE Algorithm to Prediction of
Future Strong Earthquakes:
A Case Study of Greece
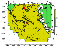
|
|
Figure 7
|
The seismological database used for calculations was derived
from the catalog of
Greece earthquakes compiled at the geophysical laboratory of the Thessalonike
Aristotle University. The catalog includes more than 40,000 earthquakes of local
magnitudes
ML 1.5 for the period
from 1964 through 1993 and is
representative (the contour
Mrep = 3.5 encompasses most of the territory
studied (Figure 7)
[Smirnov, 1997]); these characteristics enabled the
application of the prognostic MEE algorithm
[Sobolev et al., 1990, 1991;
Zavyalov et al., 1995].
1.5 for the period
from 1964 through 1993 and is
representative (the contour
Mrep = 3.5 encompasses most of the territory
studied (Figure 7)
[Smirnov, 1997]); these characteristics enabled the
application of the prognostic MEE algorithm
[Sobolev et al., 1990, 1991;
Zavyalov et al., 1995].
Over the observation time from 1964 through 1992, 36 single earthquakes with
ML  5.5 and their groups
occurred in the region studied. The unconditional
probability of the strong earthquake occurrence in this case was found to be
equal to
P(D1) = 0.1291. To differentiate the study region in accordance
with
the unconditional probability level
P(D1), we invoked data on the presence of
seismically active faults in scanning spatial cells
[Seismotectonic Map..., 1989].
Using these data, we obtained the stationary conditional probabilities of
the occurrence of a strong earthquake and false alarm equal to
P(K
5.5 and their groups
occurred in the region studied. The unconditional
probability of the strong earthquake occurrence in this case was found to be
equal to
P(D1) = 0.1291. To differentiate the study region in accordance
with
the unconditional probability level
P(D1), we invoked data on the presence of
seismically active faults in scanning spatial cells
[Seismotectonic Map..., 1989].
Using these data, we obtained the stationary conditional probabilities of
the occurrence of a strong earthquake and false alarm equal to
P(K i
| D1) = 0.8857
and
P(K
i
| D1) = 0.8857
and
P(K i
| D2) = 0.7288, respectively. Using the inferred values of
P(D1),
P(K
i
| D2) = 0.7288, respectively. Using the inferred values of
P(D1),
P(K i
| D1) and
P(K
i
| D1) and
P(K i
| D2) and the Bayesian formula
(8), we calculated a map showing the distribution of the stationary conditional probability
of strong earthquake occurrence over the territory studied (Figure 7). This map shows that the
region is divided into three zones. The probability increases to 15% in cells
including seismically active faults and decreased to 6% (about two times lower
than the value
P(D1) ) in cells in which no active faults are present.
The
probability remains the same (13%) in cells in which no data on seismically
active faults are available.
i
| D2) and the Bayesian formula
(8), we calculated a map showing the distribution of the stationary conditional probability
of strong earthquake occurrence over the territory studied (Figure 7). This map shows that the
region is divided into three zones. The probability increases to 15% in cells
including seismically active faults and decreased to 6% (about two times lower
than the value
P(D1) ) in cells in which no active faults are present.
The
probability remains the same (13%) in cells in which no data on seismically
active faults are available.
Retrospective analysis of the whole series of Greece EE maps obtained at a step
of one year for the period from 1978 through 1996 (the interval from 1964
through 1977 was used for training purposes) has shown that 48% of earthquakes
in the prediction magnitude range
ML 5.5 occurred in zones
where the
conditional probability level of such earthquakes exceeds 70%. In this case, the
average alarm area with a seismicity level of
N|ML
5.5 occurred in zones
where the
conditional probability level of such earthquakes exceeds 70%. In this case, the
average alarm area with a seismicity level of
N|ML 3.5
3.5 1 earthquake per year amounted to about 26% of the observation
area.
1 earthquake per year amounted to about 26% of the observation
area.
|
|
Figure 8
|
Figure 8 shows the EE map with a prognostic period of 1996-2002
that was
presented at the IASPEI General Assembly
[Sobolev et al., 1997, 1999].
One of the main results obtained by these authors was high potential seismic
hazard predicted for nearest years in areas east of the Athens-Thessalonica
line (area
A ) and southwest of Athens (area
B ).
The prognostic period of the map terminated at the end of
2002. Analysis of
strong ( ML 5.5 ) earthquakes
of the prognostic period in comparison with
the EE map (Figure 8) showed that four of five earthquakes of
ML
5.5 ) earthquakes
of the prognostic period in comparison with
the EE map (Figure 8) showed that four of five earthquakes of
ML 5.5 (80%)
occurred in zones of the conditional probability
P(D1 | K)
5.5 (80%)
occurred in zones of the conditional probability
P(D1 | K) 70%. Two
of these
events (40% of the total number), the strongest ( ML = 6.1) earthquakes of July
20, 1996, and November 18, 1997, occurred in zones of
P(D1 | K)
70%. Two
of these
events (40% of the total number), the strongest ( ML = 6.1) earthquakes of July
20, 1996, and November 18, 1997, occurred in zones of
P(D1 | K) 90%. The
earthquake of November 11, 1997 occurred in the zone specified as potentially
hazardous in August 1997 and this case can be regarded as a successful current
prediction of a future earthquake
[Sobolev et al., 1997, 1999].
The total area of all alarm zones in the map of Figure 8 amounted to
Sal = 45.3%
of the overall area with a seismicity level of 1 earthquake per year at
P(D1 | K) = 70%
and
Sal = 4.9% at
P(D1 | K) = 90%. Therefore, the prognostic effectiveness
of the Greece EE map of 1996-2002 in relation to strong earthquakes in zones
characterized by a given level of
P(D1 | K) was
JMEE = 1.77 for
P(D1 | K) = 70% and
JMEE = 8.16 for
P(D1 | K) = 90%.
Note that the effectiveness of the EE map in the first case virtually coincides
with the value obtained retrospectively from a long-term series of maps and is
two times higher than this value in the second case (see Figure 4)
[Zavyalov, 2002].
90%. The
earthquake of November 11, 1997 occurred in the zone specified as potentially
hazardous in August 1997 and this case can be regarded as a successful current
prediction of a future earthquake
[Sobolev et al., 1997, 1999].
The total area of all alarm zones in the map of Figure 8 amounted to
Sal = 45.3%
of the overall area with a seismicity level of 1 earthquake per year at
P(D1 | K) = 70%
and
Sal = 4.9% at
P(D1 | K) = 90%. Therefore, the prognostic effectiveness
of the Greece EE map of 1996-2002 in relation to strong earthquakes in zones
characterized by a given level of
P(D1 | K) was
JMEE = 1.77 for
P(D1 | K) = 70% and
JMEE = 8.16 for
P(D1 | K) = 90%.
Note that the effectiveness of the EE map in the first case virtually coincides
with the value obtained retrospectively from a long-term series of maps and is
two times higher than this value in the second case (see Figure 4)
[Zavyalov, 2002].
In the case of moderate earthquakes with
5.0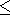 ML<5.5, only 12 of
23 events
(52%) occurred in zones with
P(D1 | K)
ML<5.5, only 12 of
23 events
(52%) occurred in zones with
P(D1 | K) 70% and
the effectiveness of the MEE
algorithm at
P(D1 | K)
70% and
the effectiveness of the MEE
algorithm at
P(D1 | K) 70% in
relation to earthquakes of
ML
70% in
relation to earthquakes of
ML 5.0 was
JMEE = 1.26, which is somewhat better than the effectiveness
in the case
of random guessing. Therefore, it is apparently inappropriate to use the MEE
algorithm for prediction of low magnitude magnitudes.
5.0 was
JMEE = 1.26, which is somewhat better than the effectiveness
in the case
of random guessing. Therefore, it is apparently inappropriate to use the MEE
algorithm for prediction of low magnitude magnitudes.
To sum up, we should note the following. Analysis of results
of seismicity
monitoring in Greece and adjacent areas over 1996-2002 has shown that the
prognostic MEE algorithm is applicable to the real-time medium-term prediction
of strong earthquakes. The effectiveness of the MEE algorithm in relation to
prediction of
ML 5.5 earthquakes is
no worse than its retrospective values
(see Figure 4)
and amounts to
JMEE = 1.77 and
JMEE = 8.16
at conditional probabilities of strong earthquake occurrence of 70% and 90%,
respectively. Application of the algorithm to prediction of weaker earthquakes
is less effective.
5.5 earthquakes is
no worse than its retrospective values
(see Figure 4)
and amounts to
JMEE = 1.77 and
JMEE = 8.16
at conditional probabilities of strong earthquake occurrence of 70% and 90%,
respectively. Application of the algorithm to prediction of weaker earthquakes
is less effective.
7. Further Improvement of the MEE Method
The MEE method described in this paper can be further improved and can be
complemented with new physically and statistically substantiated precursors that
meet the requirements described above and can be identified and used in
prognostic practice with formal procedures developed for these purposes. In the
opinion of the author, this approach offers a way for development and
improvement of the method.
In particular, the following prognostic criteria can be included in a duly
modified MEE algorithm: localization of the seismic process
[Sobolev and Zavyalov, 1984b;
Zavyalov and Nikitin, 1999, 2000],
the traveltime ratio of
P and
S waves (parameter
t )
[Slavina, 1976;
Slavina and Myachkin, 1991;
Sobolev and Slavina, 1977],
the parameter
Ksf including the fractal correction
[Smirnov and Zavyalov, 1996],
the earthquake grouping (clustering) parameter
[Vasilyev, 1994;
Zavyalov et al., 1995],
and the RTL parameter
[Sobolev and Tyupkin, 1996, 1997;
Sobolev et al., 1996].
Any of these criteria meets the requirements formulated in
the paragraph "Choice of Precursors.'' For example, no
procedures have been developed for mapping the seismicity
localization parameter and estimating its retrospective statistical
characteristics. Several precursors and prognostic algorithms
(such as RTL) have recently appeared and procedures for their use
in the MEE method have not been developed. However, these
precursors are physically substantiated and, formal procedures of
their identification being available, can be used in the MEE method.
8. Conclusion
This paper summarizes author's investigations in various aspects of physics of
the source and earthquake prediction in relation to the development of medium-term
prediction method using a complex of physically substantiated prognostic
criteria. Main results obtained in these studies are as follows.
Earthquake preparation models describing the behavior of precursors at various
stages of the preparation process provided a physical basis and imposed several
requirements to the choice of precursors for their use in the medium-term
earthquake prediction method involving a complex of prognostic criteria (the MEE
algorithm). This paper addressed the following criteria that met these
requirements and fracture this reason were accepted for their use in the MEE
algorithm: the density of seismogenic faults
Ksf, the recurrence plot
slope
g, the number of earthquakes per unit time, and
the released seismic
energy
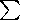 E2/3.
Their physical meaning and their relation
to the earthquake preparation process are elucidated. Based on physical ideas and
the experience of retrospective prediction using the aforementioned prognostic
criteria, we developed a model describing the behavior of these parameters during
earthquake preparation and proposed formal algorithms for their application in
prognostic practice.
E2/3.
Their physical meaning and their relation
to the earthquake preparation process are elucidated. Based on physical ideas and
the experience of retrospective prediction using the aforementioned prognostic
criteria, we developed a model describing the behavior of these parameters during
earthquake preparation and proposed formal algorithms for their application in
prognostic practice.
This paper proposed methods for collective treatment of precursors of various
types (dynamic and quasi-stationary) are based on the spatio-temporal scanning
and the Bayesian approach to the determination of the conditional probability of
strong earthquake occurrence if values of several prognostic criteria are
available, determination of their retrospective statistical characteristics, and
estimation of the prognostic effectiveness for each precursor and for the
algorithm as a whole.
Results of long-term testing of the MEE algorithm in various seismically active
regions showed that its average prognostic effectiveness
JMEE is 2.5 times
higher than in the case of random guessing. In this respect we should note that,
on average, 68% of earthquakes involved in prediction occurred in the
serviceability periods of expected earthquakes maps in zones where the
conditional probability is
P(D1 | K) 70%, and
the average area of alarm zones
amounted to 30% of the total area characterized by a seismicity level of no less
than 1 earthquake per year. These results provide an idea of the real prognostic
potential of the algorithm.
70%, and
the average area of alarm zones
amounted to 30% of the total area characterized by a seismicity level of no less
than 1 earthquake per year. These results provide an idea of the real prognostic
potential of the algorithm.
The estimates obtained in this study for the effectiveness of the precursors in
use showed that the most effective prognostic criterion used in the MEE
algorithm is the density of seismogenic faults
Ksf. Its prognostic
effectiveness was estimated at
J 4 in five of nine seismically active regions
involved in the testing procedure.
4 in five of nine seismically active regions
involved in the testing procedure.
Using various examples, the paper demonstrated the following aspects of the MEE
algorithm applications:
(i) it is applicable to prediction of the source depth of a future earthquake;
(ii) it is particularly effective for prediction of the strongest earthquakes;
(iii) the algorithm admits finer adjustment to prediction of earthquakes in
a
given range of magnitudes by comparing results obtained with various sizes of
spatial averaging cells with size estimates of the source and earthquake
preparation area as a function of the earthquake magnitude;
(iv) the algorithm can be used for medium-term prediction of strong earthquakes
on a real time scale.
Overall, this paper presented an algorithm for medium-term prediction of strong
earthquakes using a complex of physically significant prognostic criteria, with
prediction being characterized in terms of probabilistic estimates; the
effectiveness of this algorithm is several times higher than that of random
guessing prediction. Results of long-term testing indicate that the MEE
algorithm is useful for identifying zones of a high (more than 70%) conditional
probability in which observations of shorter-term precursors of other
geophysical origins should be intensified and for taking appropriate preventive
measures to mitigate economic and social damage that can be caused by a future
strong earthquake.
Acknowledgments
At various stages of this study, it was supported by the Russian Foundation for
Basic Research, project nos. 94-05-16114, 96-05-65439, and 97-05-96565; the
Program for the Support of Leading Scientific Schools in Russia, project
nos. 00-15-98578 and NSh-1270.2003.5; the International Science Foundation,
grant
nos. NFI000 and NFI300; the International Science and Technology Center, grant
no. 1745; and the Programs "Global Variations in the Environment and Climate,''
problem 2.3, and "Safety of Population and Economic Objects in Relation to
Natural and Anthropogenic Catastrophes,'' projects 2.2 (1991-1995), 1.2.1 (1996),
2.1 (1997-1998), and "Prediction of Joint Effects of Hazardous Natural Processes''
(1999-2001).
References
Adams, R. D. (1976), The Haicheng, China earthquake of 4 February 1975 - the first
successfully predicted earthquake, Int. J. Earthq. Eng. Struct. Dyn. 4(5),
423-437.
Allen, C., V. I. Keilis-Borok, I. V. Kuznetsov, et al. (1984), Long-term
prediction of
earthquakes and self-similarity of seismic precursors, California,
M 6.4, M
6.4, M 7,
in
Progress and Problems in Modern Geophysics (in Russian), pp. 152-165,
Nauka, Moscow.
7,
in
Progress and Problems in Modern Geophysics (in Russian), pp. 152-165,
Nauka, Moscow.
Allen, C., V. I. Keilis-Borok, I. M. Rotvain, and C. Hutten (1986),
A complex of long-term
seismological precursors: California and some other regions, in
Mathematical Methods in Seismology and Geodynamics (Computational Seismology,
issue 19) (in Russian), pp. 23-27, Nauka, Moscow.
Atkinson, B. (1981), Earthquake prediction, Phys. Technol. 12(2), 60-68.
Bhatia, S. C., T. R. K. Chetty, M. Filimonov, et al. (1992), Identification
of potential
areas for the occurrence of strong earthquakes in Himalayan arc region,
Proc. Indian Acad. Sci. (Earth Planet. Sci.) 101(4), 369-385.
Bongard, M. M. (1967), Recognition Problem (in Russian), 320 pp., Nauka,
Moscow.
Borovik, N. S., Earthquake prediction: Constraints on the seismic process from
observations of weak earthquakes (in relation to the identification of
prognostic criteria for strong earthquakes), in Seismic Regionalization of Eastern
Siberia and Its Geologic and Geophysical Basis (in Russian), pp. 197-213,
Novosibirsk.
Brady, B. T. (1974), Theory of earthquake, I., Pure Appl. Geophys. 112(4),
701-719.
Brady, B. T. (1975), Theory of earthquake, II., Pure Appl. Geophys. 113(1/2),
149-158.
Brady, B. T. (1976), Theory of earthquake, IV., Pure Appl. Geophys. 114(6),
1131-1041.
Cai, D., Y. Fang, and W. Sui (1988), The
b -value of acoustic emission during the
complete process of rock fracture, Acta Seismol. Sinica, (2), 129-134.
Caputo, M., V. Keilis-Borok, E. Oficerova, et al. (1980), Pattern recognition
of
earthquake-prone areas in Italy, Phys. Earth Planet. Inter., 21, 305-320.
Chelidze, T. L., G. A. Sobolev, Yu. M. Kolesnikov, and A. D. Zavyalov
(1995), Seismic
hazard and earthquake prediction research in Georgia, J. Georgian Geophys. Soc.
Ser. A, Phys. Solid Earth, 1, 7-39.
Cisternas, A., P. Godefroy, A. Gvishiani et al. (1985), A dual approach to recognition
of earthquake prone areas in the eastern Alps, Ann. Geophys., 3(2), 249-270.
Construction of Alternative Models of the Seismic Process (1991), (Report
on the
Project 3.1.1. GNTP No. 18 "Global Changes in the Environment and Climate''),
163 pp., IFZ
RAN, Moscow.
Deshcherevsky, A. V., A. A. Lukk, and A. Ya. Sidorin (2003), Fluctuations
of geophysical
fields and earthquake prediction, Izv. Phys. Solid Earth, 39, 267-282.
Dobrovolsky, I. P. (1980), Earthquake preparation model, Izv. Akad. Nauk SSSR,
Fiz. Zemli (in Russian), (11), 23-31.
Dobrovolsky, I. P. (1991), Theory of Tectonic Earthquake Preparation (in
Russian), 224 pp., IFZ RAN, Moscow.
Dyagilev, R. A. (1998), Fine structure of anthropogenic seismicity under conditions
of
the Kizel coal basin, in Mining Sciences at the Threshold of the 21st Century
(in Russian),
pp. 145-152, UrO RAN, Yekaterinburg.
Evisson, F. F. (1977), Precursory seismic sequences in New Zealand, N. Z. J.
Geol. Geophys., 20(1), 19-23.
Fedotov, S. A., A. M. Bagdasarova, I. P. Kuzin, and R. Z. Tarakanov
(1969), Earthquakes and the Deep Structure of the Southern Kurile Island Arc
(in Russian), 212 pp., Nauka, Moscow.
Fedotov, S. A., G. A. Sobolev, S. A. Boldyrev, et al. (1976), Long-term
and tentative
short-term prediction of Kamchatka earthquakes, in Search for Earthquake Precursors
(in Russian), pp. 49-61, Fan, Tashkent.
Frolov, D. I. (1984), Concentration criterion of crack growth during fracture of
solids,
in Earthquake Prediction (in Russian), No. 4, pp. 46-53, Donish,
Dushanbe.
Gamburtsev, G. A. (Ed.) (1954), Problems of Earthquake Prediction (in Russian),
50 pp., AN SSSR, Moscow.
Gamburtsev, G. A. (1982), Plan of future studies on the problem "Search for and
Development of Earthquake Prediction Methods'' (in Russian), pp. 304-311,
Nauka, Moscow.
Gelfand, I. M., Sh. A. Guberman, M. L. Izvekova, et al. (1972a), On high
seismicity
criteria, Dokl. Akad. Nauk SSSR (in Russian), 202(6), 28-35.
Gelfand, I. M., Sh. A. Guberman, M. L. Izvekova, et al. (1972b), Criteria
of high
seismicity, determined by pattern recognition, edited by A. R. Ritsema,
The Upper Mantle,
Tectonophysics, 13(1-4), 415-422.
Gelfand, I. M., Sh. A. Guberman, M. L. Izvekova, et al. (1973), Recognition
of occurrence
sites of strong earthquakes, I, Pamirs and Tien Shan, in Numerical and Statistical
Methods of Seismic Data Interpretation (Computational Seismology,
issue 6) (in Russian), pp. 107-133, Nauka, Moscow.
Gelfand, I. M., Sh. A. Guberman, M. P. Zhidkov, et al. (1974a), Recognition
of occurrence
sites of strong earthquakes, II, Four regions of Minor Asia and southeastern
Europe, in Computer Analysis of Digital Seismic Data (Computational
Seismology, issue 7) (in Russian), pp. 3-40, Nauka, Moscow.
Gelfand, I. M., Sh. A. Guberman, M. P. Zhidkov, et al. (1974b), Recognition
of occurrence
sites of strong earthquakes, III, Disjunctive nodes with unknown boundaries, in
Computer Analysis of Digital Seismic Data (Computational Seismology, issue
7),
(in Russian), pp. 41-58, Nauka, Moscow.
Gelfand, I. M., Sh. A. Guberman, V. I. Keilis-Borok, et al. (1976a), Occurrence
conditions
of strong earthquakes (California and some other regions), in Research in Seismicity
and Earth Models (Computational Seismology, issue 9) (in Russian), pp. 3-91,
Nauka, Moscow.
Gelfand, I. M., Sh. A. Guberman, V. I. Keilis-Borok, et al. (1976b), Pattern
recognition
applied to earthquake epicenters in California, Phys. Earth Planet. Inter., 11,
227-283.
Geller, R. J. (1997), Earthquake prediction: A critical review, Geophys. J. Int.,
131, 425-450.
Geller, R. J., D. D. Jackson, Y. Y. Kagan, and F. Mulargia (1997),
Earthquakes cannot be
predicted, Science, 275, 1616-1617.
Gorshkov, A. I., M. Caputo, V. I. Keilis-Borok, et al. (1979), Recognition
of occurrence sites
of strong earthquakes. IX. Italy,
M 6.0, in Theory and Analysis of Seismological
Observations
(Computational Seismology, issue 12) (in Russian), pp. 3-17, Nauka, Moscow.
6.0, in Theory and Analysis of Seismological
Observations
(Computational Seismology, issue 12) (in Russian), pp. 3-17, Nauka, Moscow.
Gorshkov, A. I., G. A. Niauri, E. Ya. Rantsman, and M. A. Sadovsky
(1985), Use of gravity
data for the occurrence site recognition of possible strong earthquakes in the
Greater Caucasus, in Theory and Analysis of Seismological Information
(Computational Seismology, issue 18) (in Russian), pp. 127-134, Nauka, Moscow.
Gorshkov, A. I., M. P. Zhidkov, E. Ya. Rantsman, and A. G. Tumarkin
(1991), Lesser Caucasus
morphostructure and earthquake occurrence sites, Izv. Akad. Nauk SSSR, Fiz. Zemli
(in Russian), (6), 30-38.
Gorshkov, A. I., V. G. Kossobokov, E. Ya. Rantsman, and A. A. Soloviev
(2001), Testing
results of occurrence site recognition of strong earthquakes from 1972 through
2000, in Problems of Lithosphere Dynamics and Seismicity (Computational
Seismology, issue 32) (in Russian), pp. 48-57, Geos, Moscow.
Gurevich, G. I., I. L. Nersesov, and K. K. Kuznetsov (1960), On the interpretation
of the
earthquake recurrence law, in Proceedings of TISSS (in Russian), vol. 6,
pp. 41-53, Dushanbe.
Gusev, A. A. (1974), Earthquake prediction from statistical seismicity data, in
Seismicity and Seismic Prediction, Upper Mantle Properties and Their Relation
to the Kamchatka Volcanism (in Russian), pp. 109-119, Nauka, Novosibirsk.
Gvishiani, A. D., M. P. Zhidkov, and A. A. Soloviev (1982), Recognition
of possible
occurrence sites of strong earthquakes, X, Occurrence sites of
M 7.75 earthquakes
on the pacific coast of South America, in Mathematical Models of the Earth Structure
and Earthquake Prediction (Computational Seismology, issue 14) (in Russian),
pp. 56-67, Nauka, Moscow.
7.75 earthquakes
on the pacific coast of South America, in Mathematical Models of the Earth Structure
and Earthquake Prediction (Computational Seismology, issue 14) (in Russian),
pp. 56-67, Nauka, Moscow.
Gvishiani, A. D., M. P. Zhidkov, and A. A. Soloviev (1984), Applicability
of Andes high
seismicity criteria to Kamchatka, Izv. Akad. Nauk SSSR, Fiz. Zemli (in Russian),
(1), 20-23.
Gvishiani, A. D., A. I. Gorshkov, E. Ya. Rantsman, A. Cisternas, and
A. A. Soloviev (1988),
Prediction of Earthquake Occurrence Sites in Regions of Moderate Seismicity
(in Russian),
184 pp., Nauka, Moscow.
Hausner, G. W. (1955), Properties of strong ground motion earthquakes, Bull.
Seismol. Soc. Am., 45, 1167-1184.
Healy, J. H., V. G. Kossobokov, and J. W. Dewey (1992), A Test to Evaluation
of the
Earthquake Prediction Algorithm M8, Open File Rep. 92-401, 23 pp.,
Geol. Surv. of U.S.
Inouye, W. (1965), On the seismicity in the epicentral region and its neighborhood
before the Niigata earthquake, Kenshin Jiho., 29, 31-36.
Kagan, Y. Y. (1997), Are earthquakes predictable? Geophys. J. Int., 131,
505-525.
Katon, Y., K. Yamazaki, and R. Ikegami (1981), Temporal variation of seismic
activity
in the region of the Pacific coast of north-eastern Japan, J. Seismol. Soc. Jpn,
34(3), 323-339.
Keilis-Borok, V. I. (1959), On estimation of the displacement in an earthquake source
and source dimension, Ann. Geophys. 12(2), 205-214.
Keilis-Borok, V. I., and V. G. Kossobokov (1984), A complex of long-term
precursors for
the strongest earthquakes, in Earthquakes and Preventive Measures for Natural
Catastrophes, The 27th International Geological Congress, Moscow, USSR, August 4-14,
1984, Colloquium 06 (in Russian), vol. 61, pp. 56-66, Nauka, Moscow.
Keilis-Borok, V. I., and V. G. Kossobokov (1986), Periods of a higher occurrence
probability of the strongest earthquakes, in Mathematical Methods in Seismology
and Geodynamics (Computational Seismology, issue 19) (in Russian), pp. 48-58,
Nauka, Moscow.
Keilis-Borok, V. I., and L. N. Malinovskaya (1966), On a regular occurrence pattern
of
strong earthquakes, in Seismic Methods (in Russian), 48-58, Nauka, Moscow.
Keilis-Borok, V. I., L. Knopoff, I. M. Rotvain (1980), Long-term seismological
precursors in Sierra-Nevada, New Zealand, Japan, and Alaska, in Methods and Algorithms
of Seismological Data Interpretation (Comparison Seismology, issue
13) (in Russian), pp. 3-11, Nauka, Moscow.
Kerr, R. (1979), Earthquake prediction: Mexican quake shows one way to look for the
big
ones, Science, 203(4383), 860-862.
Kossobokov, V. G., and A. V. Khokhlov (1993), Experimental medium-term real-time
prediction of earthquakes: Testing the M8 algorithm, in Mathematical Modeling
of Seismotectonic Processes in the Lithosphere in Relation to Earthquake Prediction
(in Russian), pp. 53-60, MITP RAN, Moscow.
Kossobokov, V. G., and I. M. Rotvain (1977), Recognition of possible occurrence Sites
of
strong earthquakes, VI, Magnitude
M 7.0, in Recognition and Spectral Analysis
in Seismology (Computational Seismology, issue 10) (in Russian), pp. 3-18,
Nauka, Moscow.
7.0, in Recognition and Spectral Analysis
in Seismology (Computational Seismology, issue 10) (in Russian), pp. 3-18,
Nauka, Moscow.
Kossobokov, V. G., V. I. Keilis-Borok, and S. W. Smith (1990), Localization
of
intermediate-term earthquake prediction, J. Geophys. Res. 95(12), 19,763-19,772.
Kossobokov, V. G., V. I. Keilis-Borok, L. L. Romashkova, and J. H. Healy
(1999), Testing
earthquake prediction algorithms: Statistically significant real-time prediction
of the largest earthquakes in the Circum-Pacific, 1992-1997, Phys. Earth Planet.
Inter. 111(3-4), 187-196.
Kostrov, B. V. (1975), Mechanics of a Tectonic Earthquake Source (in Russian),
176 pp., Nauka, Moscow.
Kuksenko, V. S. (1983-1984), Kinetic aspects of the fracture process and physical
principles
of its prediction, in Earthquake Prediction (in Russian), No. 4, pp. 8-20,
Donish, Dushanbe.
Kuksenko, V. S., V. A. Pikulin, S. Kh. Negmatullaev, and K. M. Mirzoev
(1984), Long-term
prediction of earthquakes using kinetics of fault accumulation (the Nurek
storage area), in Earthquake Prediction (in Russian), No. 5, pp. 139-148,
Donish, Dushanbe.
Kuznetsova, K. I. (1976), Crack propagation pattern in a heterogeneous medium and
a
statistical model of the seismic regime, in Research in Earthquake Physics
(in Russian),
pp. 114-127, Nauka, Moscow.
Kuznetsova, K.I., L.S. Shumilina, and A.D. Zavyalov (1981), The physical sense of
the
magnitude-frequency relation, in Proc. 2nd Int. Symp. on the Analysis of Seismicity
and Seismic Hazard. Liblice, Czechoslovakia, May 18-23, 1981, pp. 27-46.
Leary, P. C. (1997), Rock as a critical-point system and the inherent implausibility
of
reliable earthquake prediction, Geophys. J. Int., 131, 451-466.
Malovichko, A. A., R. A. Dyagilev, and D. Yu. Shulakov (1998), Monitoring
of anthropogenic
seismicity in mines of the Western Urals, in Mining Geophysics 98, Proceedings
of International Conference (in Russian), pp. 147-151, VNIMI, Saint-Petersburg.
Mamadaliev, Yu. A. (1964), Spatiotemporal behavior of seismic regime parameters,
in
Problems of Regional Seismicity in Central Asia (in Russian), pp. 93-104,
Ilim, Frunze.
Meredith, P. G., I. G. Main, and C. Jones (1990), Temporal variations in seismicity
during quasi-static and dynamic rock failure, Tectonophysics, 175, 249-268.
Mikhailova, R. S. (1980a), Evolution of seismic quiescence areas and earthquake
prediction, Izv. Akad. Nauk SSSR, Fiz. Zemli (in Russian), (10), 12-22.
Mikhailova, R. S. (1980b), Aftershocks of the Alai, 1978, Earthquake, in Earthquakes
in Central Asia and Kazakhstan (in Russian), pp. 25-45, Donish, Dushanbe.
Mogi, K. (1962), Study of elastic shocks caused by the fracture of heterogeneous
materials and its relation to earthquakes phenomena, Bull. Earthq. Res. Inst.,
40(1), 125-173.
Mogi, K. (1967), Earthquakes and fracture, Tectonophysics, 5(1), 35-55.
Mogi, K. (1968a), Source locations of elastic shocks in fracturing process in rocks,
Bull. Seismol. Soc. Japan, 46(5), 1103-1125.
Mogi, K. (1968b), Some features of recent seismic activity in and near Japan (1),
Bull. Earthquake Res. Inst., Univ. Tokyo, 46, 1225-1236.
Myachkin, V. I. (1978), Earthquake Preparation Processes (in Russian), 232 pp.,
Nauka, Moscow.
Myachkin, V. I., B. V. Kostrov, G. A. Sobolev, and O. G. Shamina
(1975), Fundamentals of
source physics and earthquake precursors, in Earthquake Source Physics (in
Russian), pp. 6-29, Nauka, Moscow.
Nersesov, I. L., V. S. Ponomarev, and Yu. M. Teitelbaum (1976), The seismic
quiescence
effect associated with strong earthquakes, in Research in Earthquake Physics
(in Russian), pp. 149-169, Nauka, Moscow.
Nersesov, I. L., Yu. M. Teitelbaum, and V. S. Ponomarev (1979), Premonitory
activation of
weak seismicity as a predictor of strong earthquakes, Dokl. Akad. Nauk SSSR
(in Russian), 249(6), 1335-1338.
Osipov, V. I. (2001), Natural catastrophes at the threshold of the 21st century,
Vestn. Ross. Akad. Nauk (in Russian), 71(4), 291-302.
Petrov, V. A. (1981), On the theory of the earthquake recurrence law, Izv. Akad.
Nauk, Fiz. Zemli (in Russian), (8), 92-94.
Pod'yapolsky, G. S. (1968), On the meaning of the coefficient in earthquake statistics,
Izv. Akad. Nauk SSSR, Fiz. Zemli (in Russian), (7), 16-31.
Ponomarev, A. V. (2003), Dynamics of Physical Fields in Modeling of Earthquake
Sources
(Doct. Diss. Phys. Math.) (in Russian), 64 pp., IFZ RAN, Moscow.
Ponomarev, A. V., A. D. Zavyalov, V. B. Smirnov, and D. A. Lockner
(1997), Physical
modeling of the formation and evolution of seismically active fault zones,
Tectonophysics, 277(1-3), 57-82.
Predictions, http://mitp.ru/predictions.html
Rantsman, E. Ya. (2001), Sites of strong earthquakes: Formulation of the problem
and a
method for its solution, in Problems of Lithosphere Dynamics and Seismicity
(Computational Seismology, issue 32) (in Russian), pp. 43-47, Geos, Moscow.
Romashkova, L. L., and V. G. Kossobokov (2001), Behavior of seismic activity before
and
after the strongest earthquakes of 1985-2000, in Problems of Lithosphere Dynamics
and Seismicity (Computational Seismology, issue 32) (in Russian), pp. 162-189,
Geos, Moscow.
Romashkova, L. L., and V. G. Kossobokov (2002), A spatially stabilized scheme for
the
application of the M8 algorithm: Italy and California, in Problems of Theoretical
Seismology and Seismicity (Computational Seismology, issue 33) (in Russian),
pp. 162-185, Geos, Moscow.
Rummel, F., and G. A. Sobolev (1983), Formation of shear cracks and seismic regime
in
samples containing lower strength inclusions, Izv. Akad. Nauk, Fiz. Zemli
(in Russian), (6), 59-73.
Sadovsky, M. A. (1979), Natural fragmentariness of rocks, Dokl. Akad. Nauk SSSR
(in Russian), 274(4), 829-831.
Sadovsky, M. A. (1999), Self-similarity of geodynamic processes, in Geophysics
and Physics of Explosions (in Russian), Selected works by M. A. Sadovsky,
pp. 171-177, Nauka, Moscow.
Sadovsky, M. A., and I. L. Nersesov (1978), Earthquake prediction problems, Izv.
Akad. Nauk SSSR, Fiz. Zemli (in Russian), (9), 13-30.
Sadovsky, M. A., L. G. Bolkhovitinov, and V. F. Pisarenko (1982), On the
discreteness
property of rocks, Izv. Akad. Nauk SSSR, Fiz. Zemli (in Russian), (12), 3-18.
Sadovsky, M. A., and V. F. Pisarenko (1983), Preparation time of an earthquake as
a
function of its energy, Dokl. Akad. Nauk SSSR (in Russian), 271(2),
330-333.
Sadovsky, M. A. (Ed.) (1986), Long-Term Prediction of Earthquakes (Methodological
Guidelines) (in Russian), 128 pp., IFZ AN SSSR, Moscow.
Scholz, C. H. (1968a), The frequency-magnitude relation of microfracturing in rocks
and
its relation to earthquakes, Bull. Seismol. Soc. Am. 58(1), 399-415.
Scholz, C. H. (1968b), Experimental study of fracturing process in brittle rock,
J. Geophys. Res. 73(4), 1447-1454.
Scholz, C. H., L. R. Sykes, and Y. P. Aggarwal (1973), Earthquake prediction
- a physical
basis, Science, 181(4102), 803-809.
Seismotectonic Map of Greece with Seismological Data (1989), Inst. Geol.
Mineral
Explor., Athens.
Shamina, O. G. (1956), Elastic impulses associated with rock sample fracture,
Izv. Akad. Nauk SSSR, Ser. Geofiz. (in Russian), (5), 513-518.
Sidorin, A. Ya. (1992), Earthquake Precursors (in Russian), 192 pp.,
Nauka, Moscow.
Slavina, L. B. (1976), Methods and some results of studying the parameter
Vp/Vs from
data of near earthquakes in the Kamchatka focal zone, in Research in Earthquake
Physics (in Russian), pp. 217-230, Nauka, Moscow.
Slavina, L. B., and V. V. Myachkin (1991), Occurrence times and sites of kinematic
precursors of strong earthquakes, in Model and in situ Studies of Earthquake
Sources (in Russian), pp. 71-78, Nauka, Moscow.
Smirnov, V. B. (1997), Experience of estimating the representativeness of earthquake
catalogs, Vulkanol. Seismol. (in Russian), (4), 93-105.
Smirnov, V. B., and A. D. Zavyalov (1996), Concentration criterion of fracture with
regard for a fractal distribution of faults, Vulkanol. Seismol. (in Russian),
(4), 75-80.
Smirnov, V. B., A. V. Ponomarev, and A. D. Zavyalov (1995a), The structure
of the acoustic
regime in rock samples and the seismic process, Fiz. Zemli (in Russian),
(1), 38-58.
Smirnov, V. B., A. V. Ponomarev, and A. D. Zavyalov (1995b), Formation
and evolution of the
acoustic regime in rock samples, Dokl. Ross. Akad. Nauk (in Russian),
343(6), 818-823.
Smirnov, V. B., A. V. Ponomarev, and A. D. Zavyalov (1995c), Acoustic structure
in rock samples
and the seismic process, Physics of the Solid Earth (English translation),
vol. 31(1), 38-58.
Sobolev, G. A. (1993), Fundamentals of Earthquake Prediction (in Russian),
314 pp., Nauka, Moscow.
Sobolev, G. A. (1999), Preparation stages of Kamchatka strong earthquakes, Vulkanol.
Seismol. (in Russian), (4-5), 63-72.
Sobolev, G. A., and A. V. Ponomarev (2003), Physics of Earthquakes and Precursors
(in Russian), 270 pp., Nauka, Moscow.
Sobolev, G. A., and L. B. Slavina (1977), Spatiotemporal variations in
Vp/Vs before
strong earthquakes in Kamchatka, Izv. Akad. Nauk SSSR, Fiz. Zemli (in Russian),
(7), 91-98.
Sobolev, G. A., and Yu. S. Tyupkin (1996), Anomalies in the weak seismicity regime
prior
to Kamchatka strong earthquakes, Vulkanol. Seismol. (in Russian), (4), 64-74.
Sobolev, G. A., and Yu. S. Tyupkin (1997), Low-seismicity precursors of large earthquakes
in Kamchatka, Volcanol. Seismol., 18, 433-446.
Sobolev, G. A., and A. D. Zavyalov (1980), On the concentration criterion of seismogenic
faults, Dokl. Akad. Nauk SSSR (in Russian), 252(1), 69-71.
Sobolev, G. A., and A. D. Zavyalov (1984a), Formation of a lateral fault and the
regime of
earthquakes, in Earthquake Prediction (in Russian), No. 5, pp. 160-173,
Donish, Dushanbe.
Sobolev, G. A., and A. D. Zavyalov (1984b), Localization of seismicity prior to the
December 15, 1971, Ust-Kamchatka earthquake, Fiz. Zemli (in Russian), (4),
17-24.
Sobolev, G. A., T. L. Chelidze, A. D. Zavyalov, et al. (1990), Maps of
expected
earthquakes based on a complex of seismological criteria, Izv. Akad. Nauk SSSR,
Fiz. Zemli (in Russian), (11), 45-56.
Sobolev, G. A., T. L. Chelidze, A. D. Zavyalov, et al. (1991), The maps
of expected
earthquakes based on a combination of parameters, Tectonophysics, 193, 255-265.
Sobolev, G. A., Yu. S. Tyupkin, and A. D. Zavyalov (1997), Map of expected
earthquakes
algorithm and RTL prognostic parameter: Joint application, The 29th General Assembly
of the Int. Assoc. Seismol. Phys. Earth's Inter., Abstracts, p. 97, Thessaloniki,
Greece.
Sobolev, G. A., Yu. S. Tyupkin, and A. D. Zavyalov (1999), Map of expected
earthquakes
algorithm and RTL prognostic parameter: Joint application, Russian J. Earth Sci.
1(4), 301-309 (http://eos.wdcb.rssi.ru/rjes/rjes
- r00.htm).
Sobolev, G. A., A. D. Zavyalov, and E. N. Sedova (1994), Ethical code of
earthquake
prediction, Izv. Ross. Akad. Nauk, Fiz. Zemli (in Russian), (1), 91-93.
Sobolev, G. A., Yu. S. Tyupkin, V. B. Smirnov, and A. D. Zavyalov
(1996), A method of
medium-term prediction of earthquakes, Dokl. Ross. Akad. Nauk (in Russian),
347(3), 405-407.
Stuart, W. D. (1974), Diffusionless dilatancy model for earthquake precursors,
Geophys. Res. Lett. 2(6), 261-264.
Teitelbaum, Yu. M., and V. S. Ponomarev (1980), Swarms of weak earthquakes in relation
to
prediction of strong events, Izv. Akad. Nauk SSSR, Fiz. Zemli (in Russian),
(1), 21-33.
Tomashevskaya, I. S., and Ya. N. Khamidullin (1972), Fracture precursors in rock
samples,
Izv. Akad. Nauk SSSR, Fiz. Zemli (in Russian), (5), 12-20.
Ulomov, V. I. (2000), General seismic regionalization of the Russian Federation (OSR-97),
List of inhabited localities of the Russian Federation in seismic areas,
The OSR-97 maps of general seismic regionalization (an insert), in Building Code
and Regulations "Construction in Seismic Areas'' (SniP II-7-81
<UNDEF>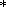 ) (in Russian),
pp. 25-44, Gosstroi, Moscow.
) (in Russian),
pp. 25-44, Gosstroi, Moscow.
Ulomov, V. I., and L. S. Shumilina (2000), A Set of General Seismic Regionalization
Maps (1:8 000 000) of the Russian Federation (OSR-97), Explanatory Note, OIFZ
RAN,
Moscow, 1999; A Map in 4 Sheets (in Russian), edited by V. N. Strakhov
and V. I. Ulomov,
Roskartografiya, Moscow.
Van Wormer, J. D., L. D. Gedney, J. N. Davies, and N. Condal (1976),
Vp/Vs and
b -values: A test of the dilatancy model for earthquakes precursors,
Geophys. Res. Lett., 2(11), 514-516.
Vapnik, V. N. (1979), Retrieval of Dependences from Empirical Data (in Russian),
448 pp., Nauka, Moscow.
Vapnik, V. N. (Ed.) (1984), Algorithms and Programs for the Recovery of Dependences
(in Russian), 464 pp., Nauka, Moscow.
Vapnik, V. N., and A. Ya. Chervonenkis (1974), Theory of Pattern Recognition
(in Russian), 416 pp., Nauka, Moscow.
Vasilyev, V. Yu. (1994), Earthquake Clustering Study (Cand. Diss. Phys. Math.
Sci.) (in Russian),
117 pp., IFZ RAN, Moscow.
Vinogradov, S. D. (1957), Acoustic observations in mines of the Kizel coal basin,
Izv. Akad. Nauk SSSR, Ser. Geofiz. (in Russian), (6), 744-755.
Vinogradov, S. D. (1959), On the distribution of pulses over energy during rock
fracture, Izv. Akad. Nauk SSSR, Ser. Geofiz. (in Russian), (12), 1850-1852.
Vinogradov, S. D. (1963), Acoustic studies in the Anna mine (Czechoslovakia),
Izv. Akad Nauk SSSR, Ser. Geofiz. (in Russian), (4), 501-512.
Vinogradov, S. D. (1964), Acoustic Observations of Rock Fracture (in Russian),
84 pp., Nauka, Moscow.
Vinogradov, S. D. (1980), Premonitory variations in seismic regime before fracture,
in
Modeling of Earthquake Precursors (in Russian), pp. 169-178, Nauka,
Moscow.
Vinogradov, S. D., K. M. Mirzoev, and N. G. Salomov (1975), Investigations
of Seismic Regime Associated with Fracture of Samples (in Russian), 118 pp.,
Donish, Dushanbe.
Wyss, M. (Ed.) (1991), Evaluation of Proposed Earthquake Precursors, Am.
Geophys. Un.
Washington D.C.
Wyss, M. (1997), Cannot earthquakes be predicted? Science, 278, 487-490.
Zavyalov, A. D. (1984a), Study of Variations in the Seismic Regime Including
Kinetics of the Fracture Process (Cand. Diss. Phys. Math.) (in Russian), 146 pp.,
Moscow.
Zavyalov, A. D. (1984b), The recurrence plot slope as a precursor of strong earthquakes
in Kamchatka, in Earthquake Prediction (in Russian), No. 5, pp. 173-184,
Donish, Dushanbe.
Zavyalov, A. D. (1986), Parameter of seismogenic fault concentration as a precursor
of
Kamchatka strong earthquakes, Vulkanol. Seismol. (in Russian), (3), 58-71.
Zavyalov, A. D. (1993), Map of expected earthquakes in the Caucasus for the period
from
1991 through 1995, in Construction of Models Describing the Development of the
Seismic Process and Earthquake Precursors (in Russian), pp. 118-120, GNTP,
Moscow.
Zavyalov, A. D. (1994), Application of MEE (Map of Expected Earthquakes) prognosis
algorithm in Greece, in Proceedings and Activity Report 1992-1994, European Seismological
Commission, 24th General Assembly, 1994 September 19-24, Athens, Greece, vol. II,
pp. 1039-1049.
Zavyalov, A. D. (2002), Testing the MEE prediction algorithm in various seismically
active regions in the 1985-2000 period: Results and analysis, Izvestiya, Phys.
Solid Earth, 38(4), 262-275.
Zavyalov, A. D. (2003a), Map of expected earthquakes in Greece for the 1996-2002
period:
Prediction and realization, Izvestiya, Phys. Solid Earth, 39, 1-6.
Zavyalov, A. D. (2003b), Retrospective testing of the MEE algorithm for western Turkey,
Izvestiya, Phys. Solid Earth, 39, 898-910.
Zavyalov, A. D., and V. I. Levina (1993), The first variant of the Kamchatka map
of
expected earthquakes, in Construction of Models Describing the Development of
the Seismic Process and Earthquake Precursors (in Russian), issue 1, pp. 177-182,
GNTP, Moscow.
Zavyalov, A. D., and Yu. V. Nikitin (1997a), Behavior of the crack concentration
parameter
preceding fracture at various scale levels, Vulkanol. Seismol. (in Russian),
(1), 65-79.
Zavyalov, A. D., and Yu. V. Nikitin (1997b), Concentration of ruptures as a criterion
of
failure preparation at different scales, Volcanol. Seismol. 19, 79-96.
Zavyalov, A. D., and Yu. V. Nikitin (1999), Seismicity localization before strong
earthquakes in Kamchatka, Vulkanol. Seismol. (in Russian), (4-5), 83-89.
Zavyalov, A. D., and Yu. V. Nikitin (2000), Seismicity localization before large
Kamchatka earthquakes, Volcanol. Seismol., 21, 525-534.
Zavyalov, A. D., and V. S. Orlov (1993), Map of expected earthquakes in Turkmenistan
and
adjacent areas, Izv. Akad. Nauk Turkm., Ser. Fiz.-Mat. Tekhn. Khim. Geol. Nauk
(in Russian), (1), 56-61.
Zavyalov, A. D., L. B. Slavina, V. Yu. Vasilyev, and V. V. Myachkin
(1995), Calculation of Expected Earthquakes Maps from a Complex of Prognostic
Criteria (in Russian), 40 pp., OIFZ RAN, Moscow.
Zavyalov, A. D., and G. A. Sobolev (1980), Some regularities of seismic regime and
earthquake prediction, Proc. 17th Gen. Assembly of ESC. Budapest, 1980, pp.65-69.
Zavyalov, A. D., and G. A. Sobolev (1988), Analogy in precursors of dynamic events
at
different scales, Tectonophysics, 152, 277-282.
Zavyalov, A. D., and Z. Zhang (1993), Using the MEE (Map of Expected Earthquakes)
algorithm in long-
and medium-term Earthquake prediction in northeast China, J. Earthquake Prediction
Res., 2(2), 171-182.
Zhang, G., and Z. Fu (1981), Some features of medium- and short-term anomalies before
great earthquakes, in Earthquakes Prediction (An Int. Review. Am. Geophys.
Un.
M. Ewing Ser.), vol. 4, pp. 497-509.
Zhidkov, M. P., I. M. Rotvain, and M. A. Sadovsky (1975), Recognition of
possible
occurrence sites of strong earthquakes, IV, High-seismicity intersections of
lineaments of the Armenia Upland, Balkans and Aegean Sea basin, in
Interpretation of Seismological and Neotectonic Data (Computational Seismology,
issue 8) (in Russian), Nauka, Moscow.
Zhurkov, S. N. (1968), Kinetic concept of the strength of solids, Vestn. Akad.
Nauk SSSR (in Russian), (3), 46-52.
Zhurkov, S. N., V. S. Kuksenko, V. A. Petrov, et al. (1977), On the rock
fracture
prediction, Izv. Akad. Nauk SSSR, Fiz. Zemli (in Russian), (6), 11-18.
Zhurkov, S. N., V. S. Kuksenko, V. A. Petrov, et al. (1980), Concentration
criterion of
rock volume fracture, in Physical Processes in Earthquake Sources (in Russian),
pp. 78-86, Nauka, Moscow.
Zubkov, S. I. (2002), Earthquake Precursors (in Russian), 140 pp., OIFZ
RAN, Moscow.
Zubkov, S. I., A. A. Gvozdev, and B. V. Kostrov (1980), A review of earthquake
preparation
theories, in Physical Processes in Earthquake Sources (in Russian), pp. 114-118,
Nauka, Moscow.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on March 23, 2005.
 7.0 occurred in the
world over the 20th century (from 1900 through 1999), and 65 of these had
magnitudes
MS
7.0 occurred in the
world over the 20th century (from 1900 through 1999), and 65 of these had
magnitudes
MS 8.0. Casualties associated
with the earthquakes of the 20th
century amounted to 1.4 million victims. Of this number, 987 thousand casualties
(about 32900 victims per year) account for the last 30 years, when human and
economic losses were fixed more accurately. According to data of the Center for
Research on the Epidemiology of Disasters (CRED) over 1965-1999, among all
natural catastrophes, earthquakes occupy third place by the number of deaths
(17% of the total number).
8.0. Casualties associated
with the earthquakes of the 20th
century amounted to 1.4 million victims. Of this number, 987 thousand casualties
(about 32900 victims per year) account for the last 30 years, when human and
economic losses were fixed more accurately. According to data of the Center for
Research on the Epidemiology of Disasters (CRED) over 1965-1999, among all
natural catastrophes, earthquakes occupy third place by the number of deaths
(17% of the total number).
 50 km and 100
50 km and 100
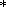 is known as the concentration
criterion of crack enlargement.
Its physical meaning consists in the fact that it characterizes the closeness of
cracks to each other and thereby their interaction and coalescence ability. The
value
K
is known as the concentration
criterion of crack enlargement.
Its physical meaning consists in the fact that it characterizes the closeness of
cracks to each other and thereby their interaction and coalescence ability. The
value
K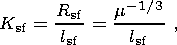
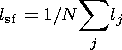 is the fault length average over the ensemble of fractures,
N is the total number
of earthquakes of the energy class range [Kmin, Kmax] that occurred in
the volume
V0 over the time
DT, and
lj is the length of an individual
seismogenic fault.
is the fault length average over the ensemble of fractures,
N is the total number
of earthquakes of the energy class range [Kmin, Kmax] that occurred in
the volume
V0 over the time
DT, and
lj is the length of an individual
seismogenic fault.
 Ksf
al, where
Ksfal is an alarm
level determined experimentally from analysis of retrospective data, are found to
be present
in a certain volume
Vi, the strong earthquake expectation period is declared
for
this volume. The critical level
Ksfal depends on the seismic activity in the
region studied, sizes of the chosen seismically active region, and energy
classes of earthquakes involved in the calculations of
Ksf.
Ksf
al, where
Ksfal is an alarm
level determined experimentally from analysis of retrospective data, are found to
be present
in a certain volume
Vi, the strong earthquake expectation period is declared
for
this volume. The critical level
Ksfal depends on the seismic activity in the
region studied, sizes of the chosen seismically active region, and energy
classes of earthquakes involved in the calculations of
Ksf. 
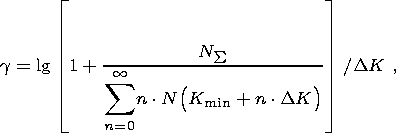
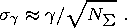
 DK) is the number of earthquakes of the energy
class
Kmin+n
DK) is the number of earthquakes of the energy
class
Kmin+n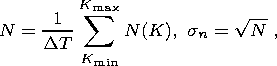
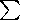 E2/3.
E2/3. 

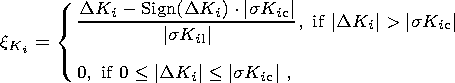
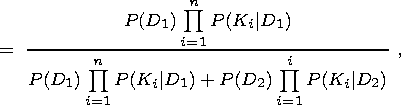
 i are used,
the unconditional probabilities
P(D1) and
P(D2) in grid cells are replaced by the stationary conditional
probabilities
P(K
i are used,
the unconditional probabilities
P(D1) and
P(D2) in grid cells are replaced by the stationary conditional
probabilities
P(K 2.39. A parameter
next in effectiveness is
Nact - Jt = 3.96
2.39. A parameter
next in effectiveness is
Nact - Jt = 3.96