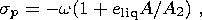
S. M. Molodensky
Schmidt Institute of Physics of the Earth, Russian Academy of Sciences, Moscow, Russia
The phenomenon of nearly diurnal free nutation of a planet with an ellipsoidal homogeneous ideal incompressible liquid core and a solid shell was discovered and examined simultaneously and independently in 1909-1910 in classical works by Hough, Sludsky, and Poincare (e.g. see [Lamb, 1945; Poincare, 1910]). This phenomenon reduces to the fact that, as the frequency of the diurnal tidal wave approaches the resonance frequency equal to
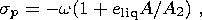| (1) |
(here w is the angular frequency of the Earth's diurnal rotation, eliq is the geometric flattening of the liquid core, and A and A2 are the equatorial moments of inertia of the whole Earth and the solid shell, respectively), the amplitude of the differential rotation of the liquid core relative to the shell increases unboundedly, which leads to an unbounded increase in the amplitude of forced nutation of the shell in space excited by this wave.
In the case of a more realistic model of the Earth including an elastic or inelastic mantle, a nonideal liquid core, and ocean, resonance amplitudes of forced nutation and tidal strain of the shell have finite values determined by the total amount of energy absorbed over the tidal cycle. Therefore, correct estimation of the resonance amplitudes should take into account not only the mantle elasticity effect on the value of sp but also all main dissipative effects.
The nearly diurnal resonance of the liquid core, influencing significantly precise measurements of amplitudes of forced nutation and diurnal earth tides, has recently been studied rather extensively. Earth models fitting best the entire set of modern astrometric and tidal gravity data were constructed [Molodensky, 2004] in order to describe dynamic tidal effects of the real Earth including a heterogeneous compressible viscous electrically conductive liquid core, inner solid core, viscoelastic shell, and ocean. In particular, analysis of these models showed that the best fit between theoretical and observed nutation amplitudes can be attained with the following values of parameters:
0.000001,
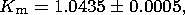 | (2) |
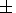0.0002, where eliq and esol are the effective dynamic flattenings of the outer liquid and inner solid cores, respectively, and Km is the dimensionless coefficient of effective inelasticity of the mantle defined as the ratio of the coefficient of mantle effective rigidity l2 (with respect to volume forces of tidal type) for diurnal oscillations to its value for oscillations at a period of 200 s (the PREM model was constructed for this period).
The value eliq = 0.002736 exceeds the hydrodynamic equilibrium dynamic flattening of the liquid core ehyd = 0.00256 by about 8%, and the value esol = 0.0053 is greater than the equilibrium flattening of the inner solid core by about two times. As was shown in [Molodensky, 2001; Molodensky and Groten, 2001], these divergences can be related to rheological properties of the mantle (due to their effect, the contemporary flattening of the liquid core can be conformable to the daily rotation velocity existing at the time 280-230 Ma, when its value and the equatorial ratio of the centrifugal force to the gravitational force was higher), as well as to the effect of the electromagnetic coupling of the liquid core with the mantle and the inner solid core, which produces an additional force moment acting on the inner solid core in the same way as the moment arising due to the ellipticity of the solid and liquid cores. With electrical conductivity values characteristic of metals at temperatures and pressures of the Earth's core, the magnetic field diffusion time is many orders greater than the period of nutation-induced oscillations of the solid core relative to the liquid core, implying that both electromagnetic and inertial coupling does not lead to tidal energy dissipation and a phase shift of the moment of electromagnetic forces relative to the moment of hydrodynamic pressure forces. Therefore, the fact that esol is significantly greater than the hydrostatic flattening of the inner solid core eh does not indicate that the real (geometric) flattening of the solid core differs from eh significantly.
In the recent epoch, the period of the nearly diurnal free nutation in space determined by values (2),
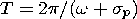 | (3) |
amounts to 434 sidereal days, which differs significantly from the solar year. However, due to a higher ratio of the centrifugal force to the gravitational force in the interval 280-230 Ma, hydrostatic flattenings of the liquid core and the mantle were also considerably higher. As is evident from formulas (1) and (3), the period of nearly diurnal free nutation decreases with an increase in eliq.
In the recent epoch, the day duration is known to increase by about 2
milliseconds per century (mainly due to dissipation of energy in shallow ocean
areas). However, estimates for remote geologic epochs (based on calculations of
cotidal maps showing the then-existing land-sea distributions) yield an
appreciably larger value. If one assumes, in accordance with
[Zharkov et al., 1996],
that an increase in the day duration over the last 280-230 Myr lie within
the range
dTday
(4-6)
103 s and the
value of the liquid core-mantle
electromagnetic coupling was nearly the same as presently, the period of nearly
diurnal free nutation in that epoch (with
dTday 5 103 s) should have
been
exactly equal to the solar year, and the frequency of retrograde annual nutation
excited by the tidal wave
Y1 should have coincided with the nearly
diurnal
resonance frequency of the liquid core.
Resonance excitation of nearly diurnal free nutation abruptly increases the amplitude of nearly diurnal oscillations of the liquid core relative to the mantle. This should give rise to two observable effects: (1) a change in the geomagnetic dynamo regime (particularly in the turbulent boundary layer at liquid core/mantle interface, where the velocity gradient of nearly diurnal oscillations is highest) and (2) an abrupt increase in tidal strain amplitudes in the mantle (determined by the dimensionless Love ( h and k ) and Shida ( l ) numbers.
The first effect can be associated with the period of anomalously rare changes in the orientation of the magnetic dipole relative to the Earth's geographic poles.
Movements of the Earth's magnetic poles (defined by the orientation of the
dipole that characterizes the main part of the geomagnetic field) are
reconstructed from paleomagnetic data. The movements of geomagnetic poles are
most clearly determined from profile data on the geomagnetic field recorded
across the strike of the Mid-Atlantic Ridge, where mantle material rises and,
upon cooling, moves horizontally eastward and westward at an average velocity of
about 2 cm yr
-1; during this process, rocks retain in their "memory'' the magnetic
field corresponding to the Curie point (the temperature at which ferromagnetic
domains are pinned). Profile data obtained at various latitudes coincide,
implying that the maximum distance between the geomagnetic and geographic poles
never exceeded a few degrees. Polarity of the magnetic dipole experienced
jumplike changes. The time of constant orientation of the magnetic dipole varies
from a few tens of thousands to 50 million years (the longest period of the
Earth's history during which the orientation did not change coincides with the
interval 280-230 Ma). The northern magnetic pole was close to the northern
geographic pole in about half of polarity change cases; the northern (southern)
magnetic pole approximately coincides with the southern (northern) geographic
pole in the other half of cases. The approximate coincidence of geographic and
magnetic poles is accounted for by a strong effect of the Coriolis force on the
convective motions in the liquid core. According to the Taylor-Proudman theorem
(e.g. see [Greenspan, 1969]),
stationary (geostrophic) flows of a rotating liquid meet the condition
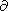v/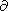
z=0, where
v is the velocity vector and the
z axis is oriented along the axis of the liquid rotation. On the strength
of this
relation, the so-called Taylor-Proudman columns oriented along the rotation axis
arise in the rotating liquid
[Greenspan, 1969];
motions in these columns are nearly axisymmetric and generate a dipole component
of the magnetic field preferably oriented along the liquid rotation axis.
An abrupt rise in mantle amplitudes of the tidal strain in the resonance time interval can lead to observed effects (e.g. the effects that are associated with the rise in the amplitude of oceanic tides excited by the wave Y1 and can be studied from data on daily and yearly nodes of fossil corals). Below, to obtain their estimates for the resonance epoch, I calculate the Love number h (determining the ratios of vertical displacements of the Earth's surface to the vertical displacement of the equipotential surface of the summarized gravitational potential of the Earth and the tide-generating potential at its surface), the Love number k (determining the ratio of the potential change due to the tidal mass redistribution inside the Earth to the tide-generating potential at its surface), and the Shida number l (determining the horizontal tidal displacements of the Earth's surface).
To estimate the effectiveness of the mechanism of resonance excitation of nearly diurnal free nutation, one should evidently take into account the effects of tidal energy dissipation due to which the resonance amplitude tends to a certain finite limit. For this purpose, resonance effects of tidal energy absorption are considered below (1) in oceans, (2) in an inelastic mantle, and (3) in a viscous core with regard for the electromagnetic coupling of the liquid core and mantle. The inelasticity of mantle in the tidal frequency range, the viscosity of the liquid core, and the core-mantle electromagnetic coupling were estimated with the use of new data on amplitudes and phases of forced nutation obtained in [Molodensky, 2000, 2004; Molodensky and Groten, 2001].
Estimates in an inelastic mantle were obtained with the use of the power-law function of creep with an exponent a [Smith and Dahlen, 1981]; in this case, the ratios of the real and imaginary parts of the shear modulus at frequencies w and w0 obey the relations (e.g. see [Zharkov et al., 1996])
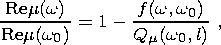 | (4a) |
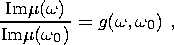 | (4b) |
where
Qm are mechanical quality parameters,
l is the depth to a spherical
layer, and
f(w, w0)
is a coefficient depending on rheological properties of
the medium. In the particular case
a
0, this dependence
includes the
Lomnitz function of creep:
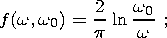 | (5a) |
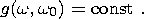 | (5b) |
In the more general case of a power function with a0, the functions f(w, w0 ) and g(w, w0 ) are given by the expressions
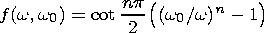 | (6a) |
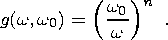 | (6b) |
As was shown in
[Molodensky, 2004],
the optimal value of
a in the range of tidal periods is
a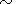 0.04,
and the quality factor
Qm in the lower
mantle (for the oscillation period 200 s) is
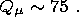 | (7) |
The values of electromagnetic and viscous coupling between the liquid core and the shell are determined by the expressions [Molodensky, 2004]
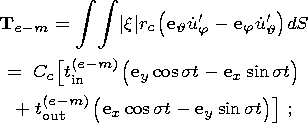 | (8a) |
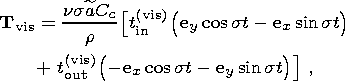 | (8b) |
where
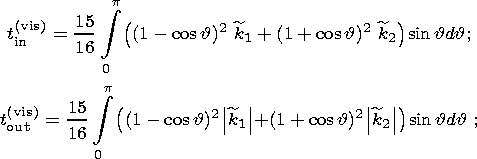 | (9a) |
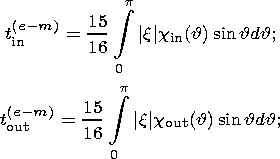 | (9b) |
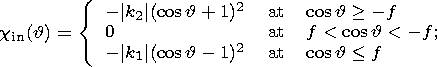 | (9c) |
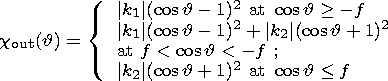 | (9d) |
|k1| and |k2| are the moduli of roots of the quadratic equation
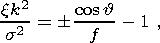 | (10a) |
corresponding to different signs of its right-hand side and f = s/(2w).
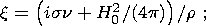 | (10b) |
n is viscosity;
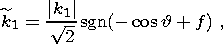 | (10c) |
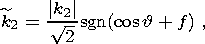 | (10d) |
H0 is the component of the magnetic field normal at the solid/liquid core and liquid core/mantle boundaries; and
 |
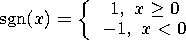is the signum function. Here Cc is the principal moment of inertia of the liquid core and the indices "in'' and "out'' denote components of moments, respectively, coinciding in phase with the moments of the tidal forces (in-phase components) and lagging behind them by p /2 (out-off-phase components).
Very few data are presently available on the angular distributions of
H0 in
the core. However, since the moment of electromagnetic forces
Cc t(e-m)in
( ey cos st -
ex sin st) coincides
in
phase with the moments of tidal forces and forces of the hydrodynamic pressure
acting on the solid/liquid core and liquid core/mantle ellipsoidal boundaries,
the
H0 distributions can be taken into account by introducing parameters
of
the effective dynamic flattening of the solid and liquid cores. Because the
coefficients
t(e-m)in determined by relation (9b)
are negative for any distributions
of the functions
x(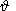
, j) (10b), the influence of this term reduces to the
fact that the effective dynamic flattenings of the inner and outer cores
esol and
eliq become greater than their geometric flattenings. Because
of deficient
data, I assume below that the values of the antiferromagnetic and viscous
coupling did not significantly varied over the last 230 Myr and, therefore,
the
deviations of
eliq and
esol from their hydrostatic values remained constant.
The resonance excitation of nearly diurnal free nutation including effects of the mantle inelasticity and electromagnetic and viscous coupling between core and shell can be described in terms of the Liouville equation for the liquid core
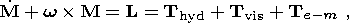 | (11) |
where
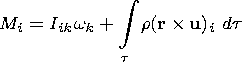 | (12) |
is the i th component of the angular momentum of the liquid core, Iik is the product of its moments of inertia, t is its volume, and L is the total moment of forces acting on the liquid core; the latter includes the moments of viscous ( Tvis ), electromagnetic ( Te-m ), and hydrodynamic pressure ( Thyd ) forces.
In the bulk of the liquid core, I describe the displacement field by expressions of the simplest (Poincare) type:
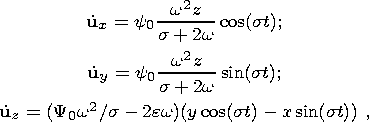 | (13) |
where y0 is a dimensionless resonance parameter determining the nutation amplitude of the liquid core relative to the shell and e is the nutation amplitude relative to the moving (Tisserand) coordinate system. The substitution of (13) into (12) yields
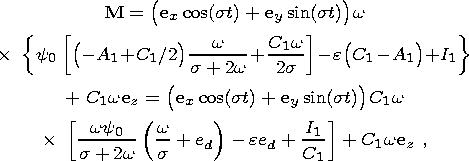 | (14) |
where A1 and C1 are the principal moments of inertia of the liquid core; I1 is the variation amplitude of inertia products determined by the relations
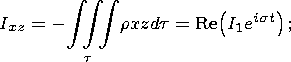 | (15) |
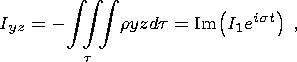 | (16) |
and ed = (C1 - A1)/C1 is the dynamic flattening of the liquid core.
In order to calculate the total moment of forces exerted by the liquid core on the shell, I calculate the moment of hydrodynamic pressure forces:
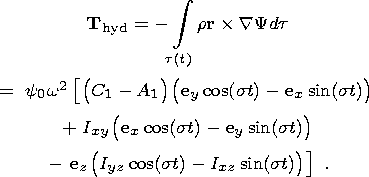 | (17) |
The substitution of relations (8a), (8b), (14) and (17) into (11) yields
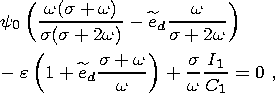 | (18) |
where
 |
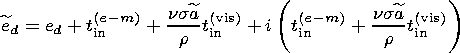- is the effective dynamic flattening of the core/mantle boundary.
The second relation connecting the parameters y0 and e can be obtained by using the continuity condition for the normal component of displacements at the core/mantle ellipsoidal boundary. The normal to this surface can be represented as
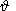) (1 - 2eg
cos2 ),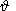
where
eg is the geometric flattening of this surface. In the
case of diurnal
tidal waves, the dependence of the normal component of displacements of the
core/mantle inelastic boundary on the angular variables ( 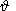, f )
and time
t can
be represented as
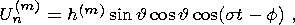 | (19) |
where
h(m) is the complex amplitude independent of ( 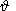, f, t ).
Then, I obtain
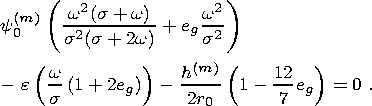 | (20) |
Equations (18) and (20) form a closed system of two algebraic equations (with complex coefficients) with respect to the two unknown complex parameters e and y0 determining amplitudes and phases of the shell nutation and tidal oscillations of the core relative to the shell near the resonance. The values of I1 and h(m) represented as coefficients in these equations were calculated for rheological models (4)-(6) in [Molodensky, 2004].
Below, I demonstrate that, with these values of parameters, the amplitude of resonance oscillations of the liquid core is about one and a half order of magnitude higher than their amplitude in the recent epoch and, consequently, the hypothesis that the geomagnetic variation pattern and the resonance excitation of nearly diurnal nutation were interrelated in the geologic epoch under consideration is fairly well substantiated.
For the numerical simulation of the resonance excitation of nearly diurnal free nutation in the interval 280-230 Ma, I used values of viscosity of the core and quality factor of the mantle from admissible ranges estimated in [Molodensky, 2002, 2004]. Because of lacking data on the temporal variation in the core-mantle electromagnetic coupling, I used its contemporary value determined by the real part of the contemporary dynamic flattening of the liquid core (see formula (2)).
Amplitude ratios of forced nutation of the real Earth to nutation of the Earth's
solid model
e/e0,
resonance parameters
Y0, and dynamic values of the Love
numbers
h and
k and the Shida number
l calculated by formulas (18) and (20)
are presented in the Table 1 for geologic epochs corresponding to various values
of the dynamic flattening of the liquid core
eliq. The first value
eliq = 2.736
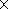10
-3, presented in this table, is the effective dynamic flattening of the
liquid core (including its electromagnetic coupling with the mantle) in the
recent epoch, whereas the value
eliq = 3.0615
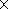10
-3 corresponds to an epoch of
approximately 280-230 Ma (more accurate dates are not presented due to
determination uncertainties in values of the secular slowing-down of the Earth's
daily rotation, although one may evidently assume that, in the first
approximation,
eliq decreases linearly with time).
As seen from the table, the Love and Shida numbers of the resonance epoch exceed their contemporary values by about two orders of magnitude, and resonance values of the factor Y0 (proportional to the amplitude of diurnal oscillations of the liquid core relative to the shell) are about 300 times greater than its contemporary values for the same retrograde annual component. The values of Y0 are about an order of magnitude higher than the amplitude of contemporary nearly diurnal oscillations of the core (excited by the main lunisolar component K1 ). Taking into account that, given turbulent friction of the core against the shell, the force of viscous friction is proportional to the second power of the resonance factor, and the absorbed energy is proportional to its third power, it is evident that the dissipation rate of tidal energy at the core/mantle boundary should have increased by a about 103 times. Therefore, the hypothesis on the interrelation between the geomagnetic variation pattern and the resonance excitation of nearly diurnal nutation 280-230 Ma is fairly plausible. Moreover, the estimate of the contribution of this effect to the history of the Earth's thermal balance is of significant interest.
Greenspan, H. P. (1969), The Theory of Rotating Fluids, p. 467, Cambridge University Press.
Lamb, H. (1945), Hydrodynamics, p. 738, Dover, New York.
Molodensky, S. M. (1981), The influence of ocean and viscosity of the shell on the Earth's nutation, Fizika Zemli, (4), 17-24.
Molodensky, S. M. (2000), Viscosity effects of the liquid core in the theory of the Earth's nutation, Izv., Phys. Solid Earth, 36, 114-120.
Molodensky, S. M. (2001), Lower mantle viscosity constraints from earth tides, nutation, and secular deceleration of rotation, Izv., Phys. Solid Earth, 37, 529-535.
Molodensky, S. M. (2004), Effect of the Electromagnetic Core-Mantle Coupling on the Earth's Nutation, 2. Comparison with Observations, Izv., Phys. Solid Earth, 40(9), 3-14.
Molodensky, S. M., and E. Groten (1997), On atmospheric excitation of out-of-phase nutational components, Astron. Astrophys., 327, 800-812.
Molodensky, S. M., and E. Groten (1998), On the dynamical effects of the inhomogeneous liquid core in the theory of Chandler wobble, Geophys. J. Int., 135, 723-726.
Molodensky, S. M., and E. Groten (2001), On the models of the lower mantle viscosity consistent with the modern data of core-mantle boundary flattening, Stud. Geophys. Geod., 45, 12-36.
Poincare, H. (1910), Sur la precession des corps deformables, Bull. Astron., 27, 321-356.
Smith, M. L., and F. A. Dahlen (1981), The period and Q of the Chandler wobble, Geophys. J. R. Astron. Soc., 64, 223-284.
Zharkov, V. N., S. M. Molodensky, A. Brzezinski, E. Groten, and P. Varga (1996), The Earth and Its Rotation, Low Frequency Geodynamics, p. 508, Herbert Wichmann Verlag, Heidelberg.