
M. K. Kaban
Schmidt United Institute of Physics of the Earth, Russian Academy of Sciences, Moscow, Russia
This work continues a series of papers investigating main properties of the density structure of the North Eurasian lithosphere [Kaban, 2001, 2002]. The present study examines density inhomogeneities of the lithosphere in relation to its stress state. Evidently, deviations from isostasy of lithosphere giving rise, for example, to isostatic gravity anomalies are directly related to the stress state of the lithosphere. There are known attempts at relating various derivatives of the gravity field and topography to the seismicity distribution (e.g. see [Artemjev, 1975; Gelfand et al., 1983]). However, until recently, such studies were restricted to the search for various empirical relations connecting, for example, gradients of isostatic anomalies with the distribution of earthquake sources. The majority of these studies were of little success, apparently because they were purely empirical rather than systematic. The present paper is an attempt to fill this gap.
The factors controlling the stress state of the lithosphere can be divided into two groups [Zoback, 1992]. The first group includes factors related to forces applied at boundaries of lithospheric plates and to large-scale movements of mantle material. The stresses associated with these factors have, as a rule, similar characteristics in fairly large regions and are usually referred to as regional stresses. The second group involves local stresses produced by heterogeneities in the structure and physical state of the crust and upper mantle, in particular, deviations from the isostatic equilibrium. Until recently, main attention was paid to the study of regional stresses. However, Artemjev et al. [1972] demonstrated theoretically that, even in an isostatically compensated lithosphere, the amplitude of local stresses due to density inhomogeneities can be of the same order as the maximum amplitude of regional stresses. Moreover, even if local stresses are relatively small, they can play the role of the triggering effect, indicating the most probable zones of rock fracture. Therefore, it is important to examine the local stress field and its relation to seismicity. Previously, the solution of this problem in terms of the real 3-D density distribution involved nearly insurmountable computational difficulties, which are virtually removed at present. One of the goals of this work is the calculation of stresses in the upper crust produced by the distribution of density inhomogeneities in the crust and upper mantle.

|
| Figure 1 |
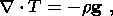 | (1) |
where
In an isotropic medium, the displacement vector
where the superscript "T '' means transposition, and
l and
m are the Lame
coefficients. Then, condition (1) can be rewritten in terms of displacements:
The total stress field can be divided into the hydrostatic and deviatoric
components. The hydrostatic component describes stresses in a horizontally
homogeneous medium and is of no interest here. In order to calculate the
deviatoric component, we assume that density inhomogeneities in each layer are
equivalent to an additional load (with appropriate amplitude and sign) applied
at the boundaries of the layer. This replacement is justified because the
thickness of the layers can always be made sufficiently small, or the position
of any boundary can be brought into correspondence with a concrete situation. In
this case, all horizontal variations in parameters relate to boundary
conditions, and the equilibrium equation without hydrostatic component is
transformed into the ordinary biharmonic equation:
We introduce a coordinate system in which the
x, y and
z axes are directed,
respectively, eastward, northward, and upward. In this case, the basic system of
boundary conditions can be written as follows:
Here,
i is the layer number,
j is the number of the boundary between the
i th
and ( i+1 )th layers, and
pj(x,y) is the load applied at the corresponding
boundary
( p1 is the topographic load, partly associated with the deformation
of the
plate, and
pn is the anomalous pressure exerted by the mantle). The
buoyancy
force is incorporated as part of the load
p. If concrete information on the
external forces applied to the system is available, these boundary conditions
can easily be modified. For example, nonzero values can be assigned to the
tangential stresses at the lower boundary, if the underplating of mantle
material should be taken into account.
Equation (4) with boundary conditions (5) is solved with the use of Fourier
transformations by the method proposed by
Kuang et al. [1989].
An infinite lithospheric plate is considered, which means that the width of the marginal
areas in the region of calculations should be significantly greater than the
effective thickness of the elastic plate. Using the density models of the crust
and upper mantle constructed in the preceding papers of this series
[Kaban, 2001, 2002],
the region of calculations can always be chosen sufficiently large,
a few hundred kilometers wider than the study area. Numerical experiments showed
that, with a maximum effective thickness of the elastic plate of about 70 km
(e.g. see
[Djomani et al., 1999]),
the enlargement of marginal areas by more
than 250-300 km did not have any significant effect on results.
Figure 1 illustrates schematically the method used for the parametrization
of a
3-D density model and converting density boundary depth variations into density
variations in relatively thin plane-parallel layers. Deviations of the real
density from the standard horizontally homogeneous model, described above, are
calculated in each layer. The lateral variations are largest if the layer is
crossed by a contrasting density boundary (e.g. the Moho). In this case, some
density variations characterize the crust, and others, with an appropriate
density difference, characterize the mantle. If the layer includes a boundary,
an average value is calculated. Thus, density variations in upper layers account
for heterogeneities in the sedimentary cover, and lower layers successively
describe the solid crust and upper mantle. All density values were taken from
the isostatic model of the North Eurasian lithosphere described in
[Kaban, 2001].
They were complemented with density anomalies corresponding to local
isostatic anomalies, i.e. the residual gravity field, which does not correspond
to the isostatic density model. These additional density anomalies were
calculated under the assumption that local isostatic anomalies are due to the
effect of the upper 20 km of the section. Preliminary calculations showed that
variations of this parameter within 10-30 km have an insignificant effect on
the
model stresses in the upper crust.
The following features distinguish the method, used in this work, from similar
previous studies
[Assameur and Mareshal, 1995;
Kuang et al., 1989].
1. Previously, only the topography and Bouguer anomalies were utilized as
initial parameters in calculations of stresses. This work uses the density model
of the lithosphere, constructed on the basis of joint analysis of the gravity
field and the data on the crust and upper mantle structure obtained by various
geological and geophysical methods. This model involves density inhomogeneities
at various levels that often do not correlate between each other. Trial
calculations showed that stresses calculated from such a model and estimates
from topography data and Bouguer anomalies differ by more than 1.5 orders of
magnitude. It is also very important to incorporate the effect of real
variations in depths to the Moho and isostatic gravity anomalies
[Kaban and Yunga, 2000].
2. In-situ values of elastic parameters estimated from seismic velocities were
used throughout the lithosphere thickness in
[Assameur and Mareshal, 1995;
Kuang et al., 1989].
The Lame coefficients varied from 3.8
It is important to determine the effective elastic moduli best fitting the real
lithosphere. Elastic models are successfully applied to analysis of media with
complex rheologies, but effective values of their elastic parameters differ
significantly from values measured in rocks (or determined from seismic
velocities). It is assumed that, with the exception of a thin surface layer,
small strains in the upper crust are approximated reasonably well by
"instantaneous'' values of elastic parameters. Supposedly, the lower crust is a
rheologically weakened layer with substantially smaller effective values of
elastic moduli
[Kusznir, 1991;
Ranalli and Murphy, 1987].
In tectonically stable continental areas, the subcrustal layer can also be described
in terms of a fully elastic rheology but, in tectonically active regions, a temperature
of 600o C critical for olivine-bearing rocks can be exceeded even in the
lower
crust, drastically decreasing the effective elastic parameters
[Burov and Diament, 1995].
The model used for the calculation of stresses was chosen
precisely from these
considerations. The main parameters of its layers are presented in Table 1. The
number of the layers was chosen in a way enabling an adequate reconstruction of
the inferred density model, including the variations in density boundaries. The
Lame coefficients in the uppermost crustal layer to a depth of 5 km are about
twice as small as the values that can be obtained by a formal conversion of
seismic velocities and this fact is due to a significant fragmentation
(fracturing) of the rocks. At greater depths, the Lame coefficients nearly
coincide with estimates obtained by the seismic velocity conversion. In
tectonically stable regions, the lower boundary of this layer reaches depths of
30-40 km but lies above a depth of 20 km in areas of high recent tectonic
activity. At greater depths, effective elastic moduli gradually decrease and
become close to zero at depths of about 70 km in stable regions and at about
35 km
in tectonically active areas. The horizontal resolution is determined by the
resolution of the initial gravity data and amounts to
10
It is evident that this distribution of elastic moduli is rather rough and at
least considerable lateral variations in their values should exist. In order to
estimate the implications of variations in these parameters, we obtained
preliminary estimates from basically different models. The model stress values
were found to be fairly stable in only the upper crust (5-20 km), where they
vary by no more than 20% in response to variations in elastic model parameters
within wide limits. However, this is valid only if large-scale blocks of the
lithosphere are isostatically compensated, i.e. in the absence of sources
producing long-wave components of the stress field. Since the latter condition
is automatically incorporated into the density model, the calculated values
should actually represent the local component of the stress field. Of course,
these results are invalid in areas where the lithosphere is fractured (for
example, near transform faults). In this work such areas are not considered.
As seen from Figure 2, the intensity (variability) of the field of isostatic
anomalies is directly related to the degree of tectonic activity (both recent
and ancient) of individual regions. The subsequent calculations account for the
total effect of all variations in the density of the crust and upper mantle on
the stress field.
The method and the lithosphere density model, described above, were used for the
calculation of six independent components of the stress tensor at
10
Some parameters of the calculated stresses and isostatic gravity
anomalies are
presented in Table 2 for several tectonic structures. It is evident that the
highest gradients of isostatic anomalies and the largest stresses in the upper
crust concentrate in contact zones of lithospheric plates, at both
continent/ocean and intracontinental boundaries. Note that these areas also
include the Baikal rift zone, where the influence of regional stresses is less
significant. The latter emphasizes an important role of local stresses
associated with heterogeneities in the lithosphere.
The method, used in this work for the calculation of stresses, involves several
assumptions (for example, on rheological properties of the lithosphere) that can
significantly affect the results. Therefore, the comparison of model estimates
with experimental data is of critical importance. Information required for such
a comparison can be recovered from analysis of seismicity. It is also important
to choose an area where density inhomogeneities of the lithosphere and upper
mantle are a major controlling factor as compared with external forces
associated with the interaction between plates.
Results of the stress calculations were compared with seismicity parameters in
an area adjacent to the Baikal rift zone
[Kaban and Yunga, 2000].
This area was chosen for the following reasons. First, the Baikal rift is relatively
far from plate collision zones and one may suppose that the stress state in the area
is
controlled by density inhomogeneities of the crust and upper mantle to a much
greater extent than in other areas (for example, near collision orogens).
Second, the Baikal rift zone is characterized by a high seismicity level,
thereby validating the comparison with results of the calculations.
Thus, even qualitative analysis of the calculated stresses with the distribution
of earthquakes indicates that these stresses are actually a part of the total
field of stresses in the lithosphere. The next step is quantitative comparison
of the results with information that can be gained from the analysis of focal
mechanisms. This task was carried out in
[Kaban and Yunga, 2000].
Focal mechanisms of earthquakes in the Baikal rift zone have been investigated
for more than 40 years (e.g. see
[Balakina et al., 1996;
Doser, 1991;
Solonenko et al., 1996].
More than 3000 earthquakes have been studied; 200 of these events
were characterized by individual mechanisms, and the remaining events, by group
(or compound) mechanisms. These results are used in the analysis presented
below.
The method consists in the comparison of predominant tendencies in the direction
and type of seismotectonic deformations with patterns of stresses calculated in
this work. Main features of the comparison method are as follows. First of all,
the resulting tensors of stress and focal mechanisms were represented by their
matrices decomposed into two main parts describing the shearing and generalized
plane components. Relative intensities of these parts can be expressed in terms
of a single angular parameter
To summarize the entire dataset, we used a formal technique
based on the
isometric transformation of data. In this approach, statistics of the shearing
components of both focal mechanism and stress tensors are imaged as clouds of
points in stereographic diagrams. Then, preferred orientations of these
components are identified by eigenvalue analysis of structural matrices
calculated as dyadic products of the vectors corresponding to the points of the
diagrams. The results are presented in Table 3
[Kaban and Yunga, 2000].
To calculate the structural matrix corresponding to the classification diagram
of stresses, the sum of 1731 dyads was used, and the number of dyads was 3271 in
the case of focal mechanisms. The intensity analysis of normalized structural
matrices showed that they are nonrandom on a level of at least 0.99.
Thus, we arrive at the conclusion that the calculated values
of stresses in the
lithosphere reliably characterize at least the local component of the complete
field of stresses. We should emphasize that the values of the difference between
the maximum and minimum principal values of the stress tensor
S1-S3 can
exceed the first critical value (7 MPa) even in stable regions (Table 2) and
thereby play a significant role in the occurrence of intraplate earthquakes.
The stress state of the lithosphere is controlled by many factors whose
significance depends on tectonic conditions of specific structures and regions.
The main goal of this paper was to emphasize the importance of the study of
stresses produced by density inhomogeneities in the crust and upper mantle.
The analysis carried out in this paper showed that the upper crust values of
local stresses are on the order of magnitude comparable with maximum stress
amplitudes determined by instrumental methods. Undoubtedly, the method used for
this analysis is of limited application, particularly in areas including
interplate boundaries. However, in areas remote from interaction zones of
lithospheric plates, this method provides results that are consistent, at least
qualitatively, with the real distribution of stresses in the lithosphere.
Comparison between the distributions of earthquake sources and calculated stress
amplitudes supports this conclusion.
The calculated parameters of the stress state in the lithosphere of the Baikal
rift and adjacent areas agree with their estimates derived from analysis of
earthquake records. Two critical values are shown to be inherent in such an
important parameter of the stress field as the difference between the maximum
and minimum principal values of the calculated stress field. The first critical
value, amounting to 7 MPa, manifests the appearance of
M>3 earthquakes and
is attained even in some parts of stable platform regions. The second critical
value (33-35 MPa) is associated with another abrupt rise in seismicity, largely
due to strong ( M>5 ) earthquakes. Thus, one may state that, even if regional
stresses play a predominant role, local stresses can serve as a triggering
effect and have a significant effect on the seismicity level within limited
areas where regional stresses vary weakly.
Comparison of the calculated stresses with parameters estimated from the
analysis of earthquake focal mechanisms shows that the most stable
characteristics of the complete stress field, obtained by this method in the
upper continental crust, are associated with shearing stresses. The latter give
rise to subvertical movements on local intraplate boundaries.
It is important to note that, even within stable platform
regions, the model
stresses can reach rather large values (up to 20 MPa, see Table 2). One
may
suppose that, in such areas, density inhomogeneities in the crust and upper
mantle due to various factors can play a predominant role in the generation of
earthquakes. This phenomenon needs additional analysis that will continue the
present study.
Artemjev, M. E. (1975), Isostasy of the USSR Territory (in Russian), 215 pp.,
Nauka, Moscow.
Artemjev, M. E., V. I. Bune, V. A. Dubrovsky, and N. Sh. Kambarov
(1972),
Seismicity and isostasy, Phys. Earth Planet. Inter., 6, 256-262.
Assameur, D. M., and J.-C. Mareshal (1995), Stress induced by topography and crustal
density heterogeneities: implication for seismicity of southeastern Canada,
Tectonophysics, 241, 179-192.
Balakina, L. M., A. I. Zakharova, A. G. Moskvina, and L. S. Chepkunas
(1996),
Natural relation of focal mechanisms of earthquakes with a geological structure of
areas,
Izv. Ross. Akad. Nauk, Fiz. Zemli (in Russian), (3), 33-52.
Burov, E. B., and M. Diament (1995), The effective elastic plate thickness (Te) of
continental lithosphere: What does it really mean? J. Geophys. Res., 100,
3905-3927.
Djomani, Y. H. P., J. D. Fairhead, and W. L. Griffin (1999), The flexural
rigidity of
Fennoscandia: Reflection of the tectonothermal age of the lithospheric mantle,
Earth Planet. Sci. Lett., 174, 139-154.
Doser, D. I. (1991), Faulting within the western Baikal rift as characterized by
earthquake studies, Tectonophysics, 196, 87-107.
Gelfand, I. M, S. A. Guberman, V. I. Keilis-Borok, L. Knopoff, F. Press,
E. Y. Ranzman, I. M. Rotwain, and A. M. Sadovsky (1983),
Pattern recognition applied to
earthquake epicenters in California, Workshop on Pattern Recognition and Analysis
of Seismicity, CA: International Atomic Energy Agency, Vienna, Austria, International
Centre for Theoretical Physics, Trieste.
Kaban, M. K. (2001), A gravitational model of the crust and upper mantle of North
Eurasia, 1. Mantle and isostatic gravity anomalies, Russian J. Earth Sci.,
3,
(3), 143-163.
Kaban, M. K. (2002), A gravity model of the north Eurasia crust and upper mantle:
2. The
Alpine-Mediterranean foldbelt and adjacent structures of the southern former
USSR, Russian J. Earth Sci., 4, (1), 19-33.
Kaban, M. K., and S. L. Yunga (2000), The effect of density inhomogeneities on the
stress
state and seismicity of the Baikal lithosphere, Dokl. Russ. Akad. Nauk (in
Russian), 371,
527-531.
Kuang, J., L. T. Long, and J. C. Mareshal (1989), Intraplate seismicity
and stress in the
southeastern United States, Tectonophysics, 170, 29-42.
Kusznir, N. J. (1991), The distribution of stress with depth in the lithosphere:
Thermo-rheological
and geodynamic constraints, Philos. Trans. R. Soc. London, 337, 95-110.
Ranalli, G., and D. C. Murphy (1987), Rheological stratification of the lithosphere,
Tectonophysics, 132, 281-295.
Solonenko, A. V., N. V. Solonenko, V. I. Melnikova, and S. L. Yunga
(1996),
Seismicity and Seismic Regionalization of North Eurasia (in Russian), issue 2/3,
pp. 363-371, Moscow.
Yunga, S. L. (1996), Seismotectonic deformations and stresses in fold belts of
Neotectonic activisation of Northern Eurasia, Izv. Ross. Akad. Nauk, Fiz. Zemli
(in Russian), (12), 37-58.
Zoback, M. L., et al. (1992), World stress map - maximum horizontal stress orientation,
J. Geophys. Res., 97, (B8) (Application), 1992.
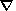 is the Hamiltonian operator.
is the Hamiltonian operator.
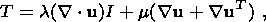
(2) 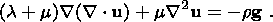
(3) 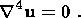
(4) 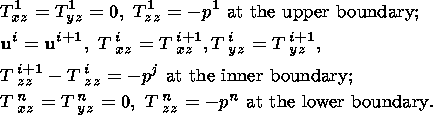
(5) 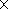 10
10 Pa at the surface
to 6.8
10
10 Pa at the surface
to 6.8
 10
10 Pa at a depth of 100 km. In this case, the effective thickness
of
elastic lithosphere exceeds 120 km, which is significantly greater than the
estimates derived from the study of the lithosphere response to an external load
at times on the order of 10
5 years and more (e.g.
[Burov and Diament, 1995]).
10
10 Pa at a depth of 100 km. In this case, the effective thickness
of
elastic lithosphere exceeds 120 km, which is significantly greater than the
estimates derived from the study of the lithosphere response to an external load
at times on the order of 10
5 years and more (e.g.
[Burov and Diament, 1995]).
3. Modeling Results
Effective Rheological Characteristics of the Lithosphere

 15
15 (approximately 19
(approximately 19
 18 km).
18 km).
Local Stresses in the Upper Crust of North Eurasia
As mentioned above, the isostatic gravity anomalies calculated in
[Kaban, 2001]
provide much more authentic constraints on local stresses in the upper
lithosphere compared to the same anomalies estimated by other authors with the
use of standard schemes of the isostatic compensation (e.g. see
[Artemjev, 1975]).
First, their calculation incorporated specific features of
the upper
crust structure (for example, thickness and density variations of low-density
sediments) and, second, the isostatic compensation models fitting the real
structure of lithosphere were used. Importantly, the long-wavelength component,
caused by the effect of deep density inhomogeneities far below the lithosphere
[Kaban, 2001],
was eliminated from the total field of isostatic anomalies. The
resulting local isostatic anomalies are shown in Figure 2.
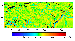
Figure 2

 15
15 grid
nodes at a depth of 12.5 km. This depth was chosen on the basis of the
aforementioned considerations. At greater depths, effective elastic moduli
depend significantly on several factors that can vary strongly within the region
studied. Preliminary tests showed that the stresses calculated in the upper
crust gradually vary with depth: the short-wave component, caused by sharp
lateral variations in the topography and shallow density inhomogeneities,
becomes somewhat smoothed with depth. Thus, values calculated at depths of 10 to
15 km characterize the upper crustal layer as a whole and can be compared with
seismicity data.
grid
nodes at a depth of 12.5 km. This depth was chosen on the basis of the
aforementioned considerations. At greater depths, effective elastic moduli
depend significantly on several factors that can vary strongly within the region
studied. Preliminary tests showed that the stresses calculated in the upper
crust gradually vary with depth: the short-wave component, caused by sharp
lateral variations in the topography and shallow density inhomogeneities,
becomes somewhat smoothed with depth. Thus, values calculated at depths of 10 to
15 km characterize the upper crustal layer as a whole and can be compared with
seismicity data.
Figure 3 shows values of the difference between the maximum
and minimum
principal values of the stress tensor
S1-S3 (the twofold maximum
tangential stress 2
t ) obtained after diagonalization of the
stress tensor
T. This parameter can be regarded as one of the most general characteristics
of
the stress state of lithosphere. As seen from Figure 3, its values reach 150 MPa,
which is on the order of magnitude comparable with maximum amplitudes of
stresses determined by seismic methods
[Zoback, 1992].
Tectonically active areas coincide on the whole well with areas of higher tangential
stresses
tmax.
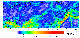
Figure 3
Another important parameter characterizing the calculated
field of stresses is
the quantity
s 2xz + s 2yz
whose distribution over the study region
is shown in Figure 4.
Higher values of this parameter can be related to areas where subvertical
movements at boundaries of lithospheric blocks are most probable and is
sometimes referred to as the shearing stress. It is important to note that its
value is weakly affected by the regional stress field, which enables direct
comparison the calculated values with its estimates from seismic data.
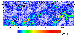
Figure 4
4. Comparison of Model Stresses With Seismicity
Figure 5 shows values of the difference between the maximum
and minimum
principal values of the stress tensor
S1-S2 (2
tmax ) in the Baikal rift
region. Also shown are epicenters of
M>5 earthquakes. Nearly all epicenters
lie within the higher stress area and, moreover, one may state that even local
features of seismically active regions correlate well with areas of higher model
stresses. For example, the seismically passive northern part of Lake Baikal is
characterized by relatively low stresses, whereas higher stresses are observed
in its southern part.
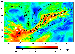
Figure 5
Figure 6 plots the relative numbers of earthquakes of
M>3 and of
M>5 as a
function of the parameter
S1-S3 (2
tmax ). As is clearly seen from
these
plots, the number of earthquakes becomes appreciable at stress values of about 7 MPa
and remains nearly constant until values of 33-35 MPa at which the second,
more abrupt increase in their number takes place. This second jump is mainly due
to the rise in the number of strong earthquakes. Thus, these two stress values
can be regarded as critical for earthquake generation.

Figure 6
5. Conclusion
Acknowledgments
Much work on comparison of the calculated stresses with focal
mechanism data was done in cooperation with S. L. Yunga, to whom I particularly
grateful.
The method used for the stress calculation was widely discussed with Sh. A. Mukhamediev.
This study was supported in part by the Russian Foundation for Basic Research,
project no. 01-05-64381
References
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on July 14, 2004.