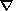 p0 is compensated for by
gravity:
p0 is compensated for by
gravity:
S. M. Molodensky
Schmidt United Institute of Physics of the Earth, Russian Academy of Sciences, Moscow, Russia
The study of local heterogeneities in the crust and upper mantle by traditional seismic methods is largely complicated due to uncertainties in the parameters of earthquake sources. The method of controlled vibratory sounding is free from this problem, but its application requires expensive sources of seismic signals, and their effective application is often inappropriate. The lunisolar tides are excited by natural sources of tidal forces, whose values are known with a reasonably good accuracy at all time moments. Therefore, in many cases the use of data on the material response to tidal forces seems quite advantageous for the study of mechanical properties of the medium. We should also note that tidal data differ from seismic evidence in that they provide information on the properties of the medium in the range of much lower frequencies (diurnal and semidiurnal periods). Because of this distinction, comparison of seismic and tidal data can provide constraints on both the elastic moduli and rheological properties in the vicinity of an observation point.
In recent years, the most significant anomalies of tidal tilt and strain factors have been discovered in the vicinity of the Orenburg gas-condensate field and in the Baksan Gorge at the foot of the Elbrus Mountain. In both cases, this appears to be related to the presence of a cavity (possibly containing a rigid skeleton) significantly differing in average shear modulus from the surrounding medium. Analysis of the response of this cavity to tidal forces allows one to estimate (1) the sizes of this cavity and mechanical properties of its upper dome and, based on the estimated thickness of the dome and its effective rigidity, (2) the criteria of its stability (this problem is very important in relation to the possible collapse of the dome due to the pumping-out of gas).
Along with the detection of local heterogeneities, there also exists the problem of identifying global lateral heterogeneities in the mantle, which should primarily give rise to anomalies in the tidal gravity factor d (its value is mainly dependent on mechanical properties of the lower mantle and nearly insensitive to local heterogeneities in the vicinity of an observation point).
Below, we derive general relations for the determination of radial and tangential components of displacements and variations in the gravity potential at the Earth's surface with laterally inhomogeneous distributions of elastic moduli. Numerical estimates are presented for the effect of local inhomogeneities of elastic moduli on tidal tilts and deformations.
Partial differential equations in a general form governing the elastic-gravitational
conditions of the Earth under the action of tidal forces are based
on the assumption of an initial (nondeformed) hydrostatic equilibrium of the
mantle and crust, implying that the pressure gradient
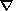 p0 is compensated for by
gravity:
p0 is compensated for by
gravity:
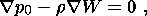 | (1) |
where r is density; W is the unperturbed gravitational potential, satisfying the Poisson equation
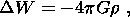 | (2) |
and G is the gravitational constant.
Elastic tidal deformations displace an element of the medium from a point
determined by the radius vector
where
dik is the Kronecker delta and
sik is the tensor of elastic stresses
connected with the displacement vector through the Hooke law
Substituting (3-6) into the equation of elastic equilibrium and subtracting,
respectively, (1) and (2) from the results, we obtain
Applying the curl operator to the left- and right-hand sides of (1) yields
Adding the identically zero term
to the left-hand part of Equation (7a), this equation takes the form
(henceforward, summation is assumed under repeated indexes and
no distinction is
drawn between covariant and contravariant components of vectors and tensors,
i.e. all calculations relate to a Cartesian system of coordinates).
To describe tidal deformations in a radially and laterally heterogeneous medium,
we use Equations (8) and (7b) with the inhomogeneous boundary conditions
where
S and
To calculate the Green function for the boundary problem (8), (7b), (9a), (9b),
we will write relations generalizing the Betti theorem of reciprocity to the
case of tidal deformations of a gravitating medium with a hydrostatic
distribution of initial stresses.
In order to solve an inhomogeneous equation of the form
where
F (
which satisfy the boundary conditions
Here
is the density of the single layer on the Earth's surface,
er is the unit radius
vector and
ymn are normalized spherical functions.
Taking into account the explicit form of the operator
reduces to the surface integral
where the density of the single layer
D1 is determined by a relation similar to
(12):
If we set
F ( r) = 0 in (10a), i.e. if the solution of homogeneous tidal
equations in the absence of external forces is taken as ( u(1), V(1) ), volume
integral (13a) vanishes identically, and relation (13b) generalizes the Betti
theorem of reciprocity to the case of a gravitating medium with a hydrostatic
distribution of initial stresses. The terms
in (13b), corresponding to the
theorem of reciprocity, determines the difference between the values of the work
done by surface forces acting through the displacements
u(j) (corresponding
to the solution
( u(1), V(1)) ) and by surface forces acting
through the
displacements
u(1) (corresponding to the solution
( u(j), V(j)) ); the
additional terms
determine the difference between the gravitational energies
of the single layer
D1 in the field with the potential
R(j) and the single
layer
D(j) in the field with the potential
R1.
If the external body forces
F(
which is helpful for the construction of the Green function related to
the
problem of elastic deformations of a gravitating medium produced by the given
external body forces
F(
Indeed, if external surface forces are absent, we have
s1
which completely defines the three components of the sought-for vector
u1 at
any point
r0 of the surface
s.
Analogically, specifying the solutions ( u(j), V(j) ) by the boundary
conditions
s(j)
which completely defines the potential variations on the Earth's surface.
Tidal displacements and the potential in spherically symmetric models of
the
Earth are determined by the Love formula
where
k=0, 1 and 2 for long-period, diurnal and semidiurnal tidal components,
respectively.
When a horizontally homogeneous model of a medium (with distributions of density
r0(r) and elastic moduli
l0(r) and
m0(r) ) is replaced by a
spherically
nonsymmetrical model (with distributions
r0(r) + dr, l0(r)
+ dl and
m0(r) + dm ), the solutions ( u0, R0 )
of Equations (8) and (7b) acquire increments ( u1, R1 ).
In the first approximation of the perturbation theory, the equations of tidal
strain in a laterally and radially heterogeneous medium can be written as
where
and
The general solution to the problem of tidal strain in a horizontally
heterogeneous medium is sought as the sum of spheroidal and toroidal spherical
harmonics:
Auxiliary solutions ( u, R(j) ) determining the Green function are
represented as
expressions of the same form as the terms in (20a) and (20b) at
j=4:
and
Here
fi(r) is a system of six functions defined by the
ordinary differential
equations
with the coefficients
The symmetry properties of the coefficients
aik in (23) are due to the self-conjugacy
of the operator
L (8)
[Molodensky, 1984].
The boundary conditions for the solutions ( u(j), R(j) ) are defined
as follows:
Then, substituting (20) and (21) into (13), we find
Here
These relations completely define all of the sought-for coefficients in
expansions (20a) and (20b).
In order to numerically calculate the Green function in a heterogeneous medium,
we express the components of the tidal displacement vector through homogeneous
harmonic polynomials
xnm = rn
ymn (
and the Laplace equation
Expressing the displacement vectors
u0 and
u(j) through
xnm, we obtain
where
x0 = r2 yj2
(
Now, we address the solutions of tidal equations in the case of arbitrary
lateral variations in elastic moduli. Then, integral (26) takes the form
where
Using the Gauss theorem and taking into account the condition of vanishing
stresses at the outer surface,
we obtain
The substitution of (19d) into (20) yields
where
and
Substituting (29a) and (29b) into (31c), we obtain
Taking into account (27), we have
The expansion of the lateral inhomogeneities of elastic moduli in series
of
harmonic functions yields
Taking into account (32)and (33), the integrals in (31b) and (31c) can
be
represented as the sum of terms containing integrals of products of three
harmonic polynomials, scalar products of their gradients, and the convolution of
the tensors consisting their second derivatives and having the form
where
For calculating the integrals of products of three harmonic polynomials,
we substitute the relation
xnm = rn
ymn (
Here
Alpnmn0m0 is the integral
of the product of three spherical functions with the
respective indexes ( l, p ), ( n, m ) and ( n0, m0 ) taken over the surface of
a unit sphere.
The second term in formula (33b) contain the product of the homogeneous
harmonic polynomial
xlp and the scalar product of
the polynomial gradients
(
Integrating (35) by parts and taking (27) into account, we find
and two similar relations obtained from (36) by the cyclic permutation
of the
polynomials
xlp, xnm,
xn0m0.
Solving these equalities, we find
The third term in (33b), containing the volume integral of the convolution
of
tensors that consist of the second derivatives of homogeneous harmonic
polynomials of the form
can be calculated in a similar way. Denoting
and integrating (38) by parts, we obtain
where
Taking (27) into account, we have
and, therefore,
Integrating
Jn0m0 (3)lpnm
by parts, we obtain
Applying the cyclic permutation of indexes ( l, p)
or, substituting (37),
The substitution of (42) and (45) into (39) yields
With the help of (37) and (36), expression (32) is transformed into the
final
form
In analyzing local effects of heterogeneity of a medium on tidal tilts and
strains, it is sufficient to consider the simplest model of an elastic and
nongravitating half-space.
We consider a system of two auxiliary solutions (corresponding to the values
j =1 and 2) of the homogeneous equations
with boundary conditions of the delta function type at the outer surface
(corresponding to the cases of tangential and normal concentrated loads applied
at a point ( x0, y0, 0 ):
Here ( x, y, z ) is a local Cartesian system of coordinates oriented
in such a
way that the
z axis is directed along the normal to a surface element and the
x axis coincides in direction with the action of load in the
j = 1 solution.
Substituting (47) and (48) into (49a) and (49b), we obtain
The expressions for the displacement vectors
u(j=1) and
u(j=2) specified by boundary
conditions (15a) and (15b) are given, for example, in
[Landau and Lifshits, 1963].
The related components of the stress tensor can be written in the
following convenient form:
Thus, the complete solution of the problem under consideration reduces
to the
calculation of integrals (50a) and (50b).
In the 2-D case (when elastic moduli do not depend on
y ), simple expressions
for tidal tilts and strains can be obtained from formulas (50a, 50b). Integrating
components (51) over
y from
-
where
we obtain
These expressions allow one to obtain relatively simple analytical solutions of
the problem of tidal deformations in an elastic half-space with heterogeneities
independent of
y. For example, if inhomogeneities of elastic moduli are
specified by a value ( dl, dm ) in a rectangular parallelepiped infinite along
the
y axis ( x1
where
and the symbol
| indicates the result of double substitution from
x1 to
x2 in
x and from
z1 to
z2 in
z.
One of the main shortcomings of the tidal method is its low immunity to the
noise produced by local disturbances in the atmospheric pressure, groundwater
level, and temperature. The first two effects are either irregular or seasonal
and can be eliminated by increasing the lengths of observation series analyzed.
On the other hand, the thermoelastic stresses involve strictly periodic diurnal
components coinciding in frequency with main solar waves, and their elimination
by averaging is ineffective.
We should note that, due to the amplitude modulation of the diurnal temperature
variations by the annual wave, this spectrum additionally contains combination
frequencies of the diurnal and annual waves with rather high amplitudes. Periods
of these waves also exactly coincide with periods of some main lunisolar tidal
components (e.g. the
Km and
Ks waves, whose period is equal to the sidereal
day), so that their elimination by methods of spectral analysis alone is also
ineffective.
Below we present results of spectral analysis of average temperature variations
in the range of tidal frequencies under the natural assumption that, when
averaged over a sufficiently long time interval, the diurnal temperature
variations are determined by the value of the solar flux incident on the unit
area of the Earth's surface and by the effects of heat capacity of the medium
leading to a constant (season-independent) phase delay of temperature. Based on
these calculations, we present model corrections to the amplitudes and phases of
main tidal waves recorded at the tidal strainmeter Protvino station. Comparison
of model results with observations is shown to be effective for obtaining
reliable estimates of the thermal expansion coefficient and bulk modulus in the
anomalous zone adjacent to the Protvino station.
The value of the solar thermal flux per unit area of the Earth's surface
is determined by the well-known expression
where
S0 is the heat flow per unit area normal to the direction toward
the Sun
and
a is the angle between the direction toward the
Sun
and, accordingly,
Here,
i, j, k is the right-handed system of the unit vectors (the unit vector
In the most general case, the expansion of flow (47) in spherical functions can
be represented in the form
Because we are further interested only in near-diurnal components of
thermoelastic waves, we can set
m = 1. The problem in question being fully
symmetrical about the Earth's rotation axis, the coefficients in (49) possess
the following properties at
m = 1:
In the case of main diurnal waves, setting
m = 1 in (55) and taking (56) into
account, (49) can be represented in the following simple form:
Numerical values of the coefficients
cn in this relation are presented in the
Table 1.
Taking into account relation (57) and the fact that the sidereal and solar days
T sid and
T sol are interrelated through the formula
it is easy to show that, at
l = 0, the coefficients
c ln in (51) describe
thermal waves having a period exactly coinciding with the solar day; the
l = 1
coefficients describe waves with a period equal to the sidereal day, and the
l = 2 coefficients correspond to the frequency which is symmetrical to the
frequency of the solar day with respect to the frequency of the sidereal day
(i.e. the period of this wave is equal to the difference of two sidereal day and
one solar day). All these frequencies are also present in the spectrum of tide-generating
forces and can therefore be eliminated from the results of tidal
observations only by numerical modelling of thermoelastic strains. Below, we
consider several examples of possible effects.
General equations describing the thermoelastic strains in a radially
heterogeneous self-gravitating model of the Earth with a hydrostatic
distribution of initial stresses can be written as
where the operator
L is defined by relation (8). Equation (59) should be
complemented with the boundary condition
( nk are components of the outer normal), describing the
absence of stresses at
the outer surface of the Earth
s.
In the case of local thermoelastic deformations (with the characteristic
horizontal size of the heated layer being much smaller than the radius of the
Earth), the effects of gravitational forces and initial hydrostatic stresses on
the thermoelastic deformations in the Earth is small, and (59) can be replaced
by the equation
which can be considered in the approximation of a homogeneous elastic half-space.
The effects of local thermoelastic deformations can be significant if the medium
contains inclusions with anomalous values of elastic moduli, the thermal
expansion coefficient and temperature. Below, we assume that variations in
elastic moduli are small compared to their average values in the surrounding
medium, whereas no limitations will be imposed on spatial local variations in
temperature and the thermal expansion coefficient.
In solving boundary problem (60)-(61) for a nongravitating medium, we may set
D = V(J) = D(j) = V
= 0. The substitution of (60)-(61) into (15) yields
The divergences of the vectors
u(j) in these relations are determined by simple
formulas:
where
r2 = (x - x0)2 + z2.
Integrals (62a) are easily calculated analytically for certain simplest models of
temperature distribution. For example, if the values
kaT are described by a
piecewise-continuous function equal to a constant
C0 = k0a0T0
in a rectangular
volume with vertexes at the points
xi, zk (i, k = 1,
2) and is zero
outside this rectangle, we have
where the symbol
| indicates the result of the double substitution from
x1 to
x2 in
x and from
z1 to
z2 in
z.
In calculating the volume integrals (62a, 62b), one should take into account that,
in
the case of diurnal temperature variations, the depth of the layer of
appreciable temperature variations is small compared to the characteristic
horizontal size of the integration domain. Expanding (64) in powers of the small
ratios
z2/(x1 - x0) and
z2/(x2 - x0), setting
z1 = 0 and differentiating with respect
to
x0, we obtain
where
exx is the horizontal component of strain along the
x axis at the point
x0.
In order to obtain a simple numerical estimate, the value
z2 in (65) can be
determined as the thickness of the layer in which the amplitude of the diurnal
temperature variations decreases by
e times. Using the equation of heat
conduction in a homogeneous half-space
b
where, as before,
w = 2p/T0
and
T0 is the sidereal day.
Figure 1
exemplifies the finite-difference modelling of the tidal strain effect
of a local heterogeneity. The spatial coordinate
x is plotted on the horizontal
axis, and the ratio of the horizontal component of tidal strain in the
heterogeneous medium to that in the homogeneous elastic half-space is plotted on
the vertical axis.
(The model is characterized by an inhomogeneous distribution of the shear modulus
m and
a constant Lame coefficient
l; the shear modulus inhomogeneity is
specified within a rectangular parallelepiped that is infinite along the
y axis
and has a 2:1 ratio of the sides along the
x and
z axes; the ratio of
distances from the outer surface to the upper and lower faces is 0.4; curve 1
is
the strain at the upper face of the parallelepiped and curve 2 is the strain
at the
half-space surface.)
The method of calculating tidal strains in a heterogeneous
medium, described
above, is particularly effective in relation to 3-D problems involving a complex
configuration of the anomalous zone (in this case, the application of the
finite-difference and finite-element approaches provides very approximate and
often unstable solutions). Figure 2 plots corrections to the
x components of
tidal tilts and linear strains for an inhomogeneity specified in a rectangular
parallelepiped with a 1:5:5 ratio of the sides along the
x, y and
z axes; in
this model variant, the shear modulus
m is constant throughout the half-space,
and the
l value within the parallelepiped is smaller by
90% (the
corrections are normalized in such a way that tilts in a homogeneous half-space
correspond to the value
g = 0.7, i.e. maximum and minimum tilts near the
vertical faces of the parallelepiped correspond to the values
g = 0.9 and 0.5,
respectively).
We estimate local variations in the parameter
C0 that are consistent with such
anomalies. A relatively rough (1:50000) map of geodynamic zones separating
blocks of the 6th to 10th orders is only available for the area around the
Protvino station; this map resolves details whose linear sizes are no less than
a few hundred meters. However, as seen from relations (20), the effects of
thermoelastic variations attenuate with distance as
1/L3, implying that the
effects of local heterogeneities indistinguishable in the map may play the major
role. Substituting the typical value
z2
With the typical values
a
Thus, a considerable summer increase in the
K1 wave amplitude at the Protvino
station is well consistent with the effects of thermoelastic deformations in the
anomalous zone near the station.
Relations (19)-(20) and the expansion coefficients of the average solar thermal
flux presented in the table can be used for numerical modelling of average
thermoelastic strains with an accuracy sufficient for applications.
Detailed comparison of results derived from the solution of the study problem by
various methods and the interpretation of data on local anomalies of tidal tilts
and strains in various regions are the subject of the next paper.
Landau, L. D., and E. M. Lifshits (1963), Theory of Elasticity (in Russian),
Moscow.
Latynina, L. A., and E. A. Boyarsky (1999), Seasonal variations in the lunar tide
as a
model of an earthquake precursor, Vukanol. Seismol. (in Russian), (in press).
Molodensky, S. M. (1977), The effect of horizontal heterogeneities in the mantle
on
tidal wave amplitudes, Fiz. Zemli (in Russian), (2), 3-8.
Molodensky, S. M. (1983a), Local anomalies in the amplitudes and phases of tidal
tilts
and strains, Fiz. Zemli (in Russian), (7), 3-9.
Molodensky, S. M. (1983b), Gravity field variations due to elastic deformations of
the
Earth, Fiz. Zemli (in Russian), (9), 3-21.
Molodensky, S. M. (1984), Tides and nutation of the Earth, 214 pp.,
Nauka, Moscow.
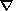
 u.
Then, the density
r
u.
Then, the density
r ,
potential
W
,
potential
W and stress tensor
s
and stress tensor
s ik
in the deformed medium can be expressed as
ik
in the deformed medium can be expressed as
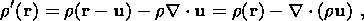
(3) 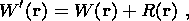
(4) 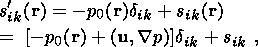
(5) 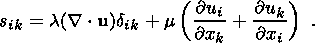
(6) 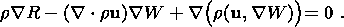
(7a) 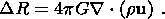
(7b) 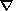 W
W 
 r = 0.
r = 0.  (
( W
W 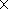
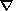 r) = (
r) = (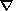 r, u)
r, u) 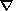 W
- (
W
- (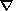 W, u)
W, u) 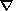 r,
r, 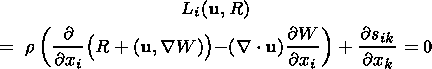
(8) 2. Generalization of the Betti Theorem of Reciprocity
to the Case
of Tidal Deformations of a Medium. Green Function
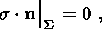
(9a) 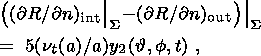
(9b) 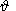 , j,
t) is the spherical function of the 2nd order;
, j,
t) is the spherical function of the 2nd order;
 , j and
t are colatitude, longitude and time, respectively; and the
indexes "int'' and "out'' indicate, respectively, inner and outer normal derivatives.
, j and
t are colatitude, longitude and time, respectively; and the
indexes "int'' and "out'' indicate, respectively, inner and outer normal derivatives.
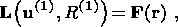
(10a) 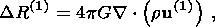
(10b) 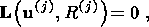
(10c) 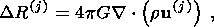
(10d) 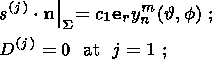
(11a) 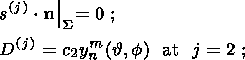
(11b) 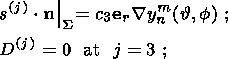
(11c) 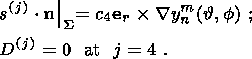
(11d) 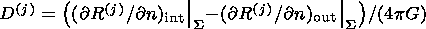
(12) 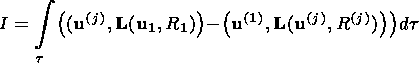
(13a) 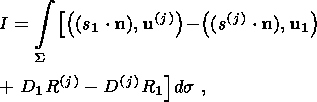
(13b) 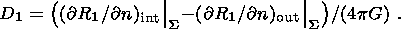
(14) 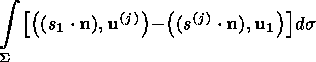
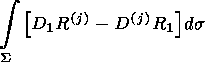
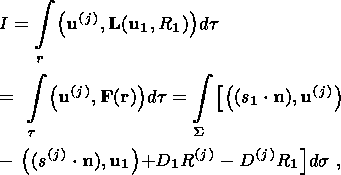
(15)  n = 0. Let
the solutions
( u(j), V(j) ) be specified
by the boundary conditions
s(j)
n = 0. Let
the solutions
( u(j), V(j) ) be specified
by the boundary conditions
s(j)  n =
e(j)d ( r - r0)
and
D(j) = 0, where
e(j) is an arbitrarily oriented vector,
d( r - r0) is the 2-D
delta function, and
n =
e(j)d ( r - r0)
and
D(j) = 0, where
e(j) is an arbitrarily oriented vector,
d( r - r0) is the 2-D
delta function, and
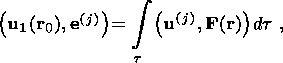
(16)  n = 0
and
D(j) = d ( r -
r0) and
integrating the right-hand part of (15) over angular variables,
we obtain the relation
n = 0
and
D(j) = d ( r -
r0) and
integrating the right-hand part of (15) over angular variables,
we obtain the relation
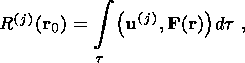
(17) 3. Application of the Perturbation Method to the Problem
of the Effect
of Horizontal Heterogeneities on Elastic Deformation of a Medium
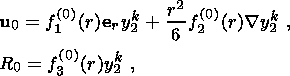
(18) 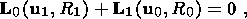
(19a) 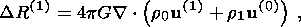
(19b) 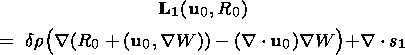
(19c) 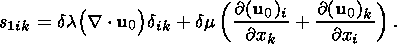
(19d) 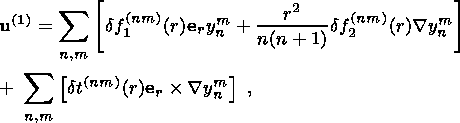
(20a) 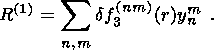
(20b) 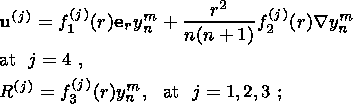
(21a) 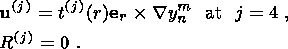
(21b) 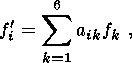
(22) 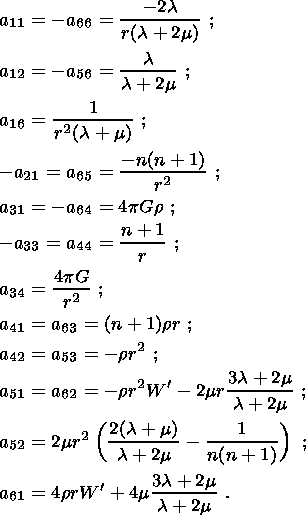
(23) 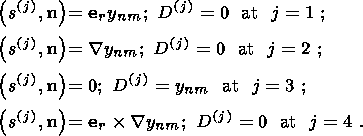
(24) 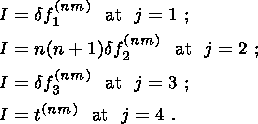
(25) 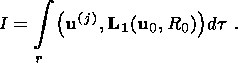
(26) 4. Green Function for the Problem of Tidal Deformations
in a Heterogeneous Medium
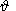 ,
j). In Cartesian coordinates
xi, they satisfy the equation
,
j). In Cartesian coordinates
xi, they satisfy the equation
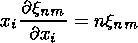
(27) 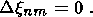
(28) 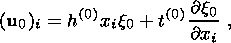
(29a) 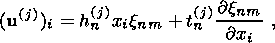
(29b) 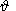 , j);
j = 0, 1 and 2 for long-period, diurnal and semidiurnal waves,
respectively; and the functions
h(j)n, t(j)n
and
h(0), t(0) depend on the radius
r alone. Comparing (18), (21a) and (29), these functions can easily be
expressed through
f(j)i(r), determined by the system
of equations (22)-(23).
, j);
j = 0, 1 and 2 for long-period, diurnal and semidiurnal waves,
respectively; and the functions
h(j)n, t(j)n
and
h(0), t(0) depend on the radius
r alone. Comparing (18), (21a) and (29), these functions can easily be
expressed through
f(j)i(r), determined by the system
of equations (22)-(23).
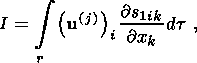
(29c) 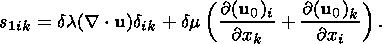
(29d) 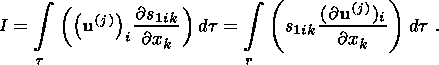
(30) 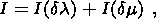
(31a) 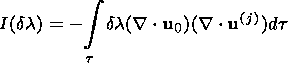
(31b) 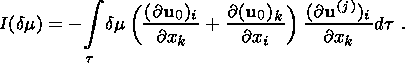
(31c) 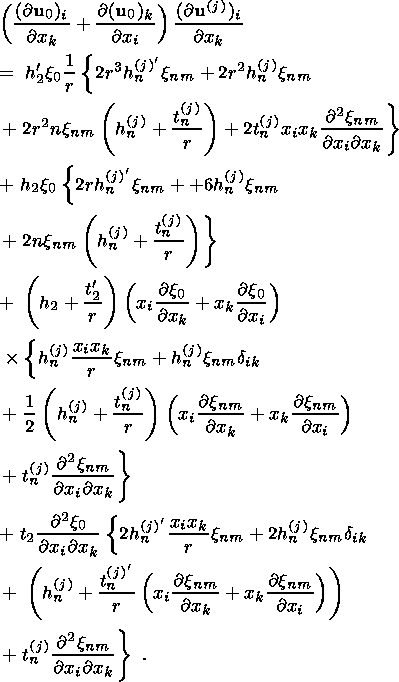
(32) 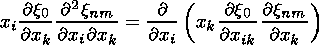
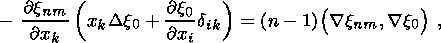
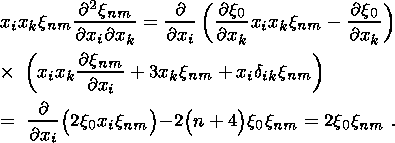
(33) 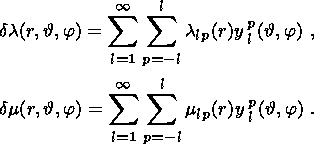
(33a) 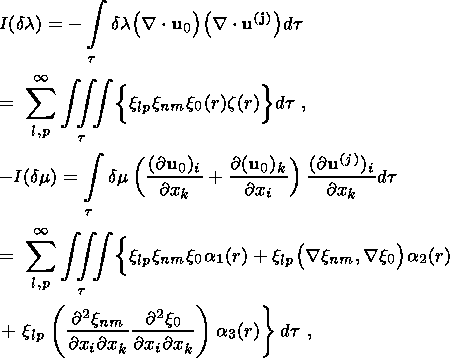
(33b) 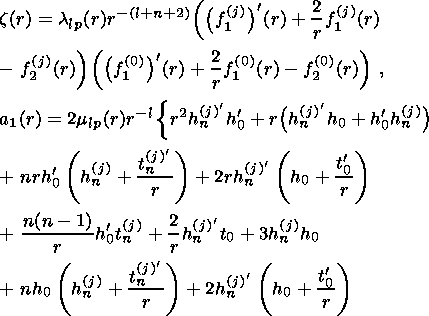
(33c) 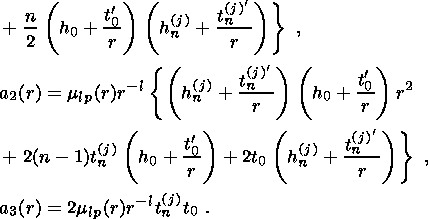
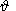 ,
j) into the
first term in (33b) and obtain
,
j) into the
first term in (33b) and obtain
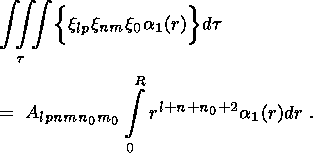
(34) 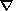 xnm,
xnm,
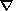 x0 )
and can be calculated as follows. Denote
x0 )
and can be calculated as follows. Denote
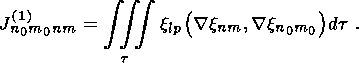
(35) 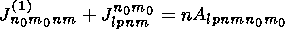
(36) 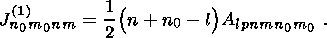
(37) 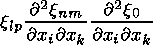
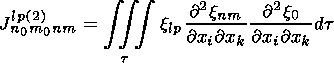
(38) 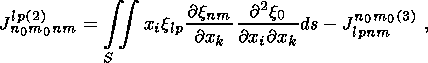
(39) 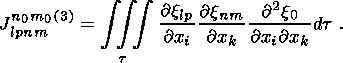
(40) 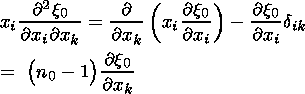
(41) 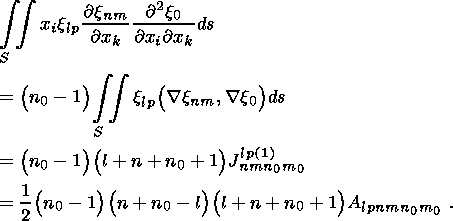
(42) 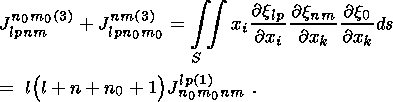
(43)  (n, m)
(n, m)  (n0, m0 ) to this
relation and determining
Jn0m0lpnm
from the resulting system of three equations, we
find
(n0, m0 ) to this
relation and determining
Jn0m0lpnm
from the resulting system of three equations, we
find
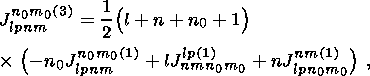
(44) 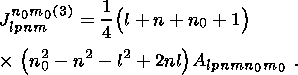
(45) 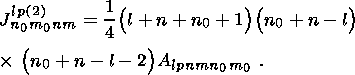
(46) 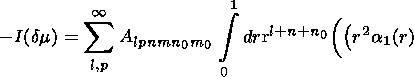
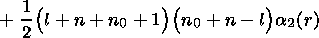
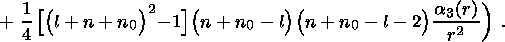
5. Tidal Deformations of a Heterogeneous Elastic Half-Space
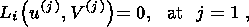
(47) 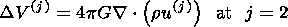
(48) 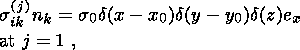
(49a) 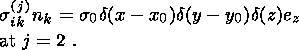
(49b) 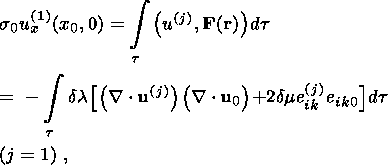
(50a) 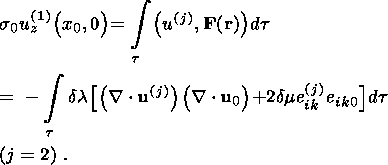
(50b) 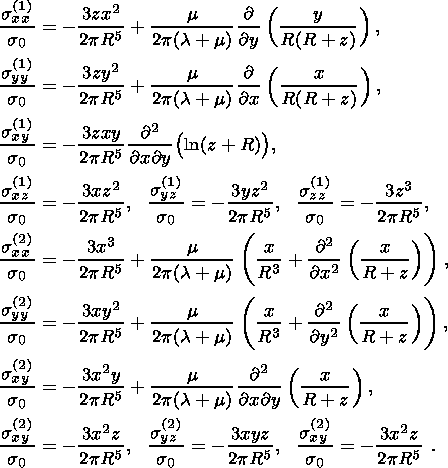
(51)  to
to
 and taking into account that
and taking into account that
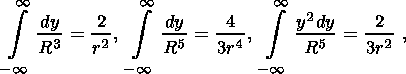
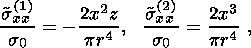
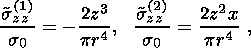
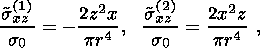
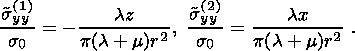
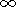
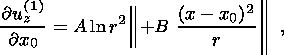
(52a) 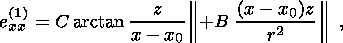
(52b) 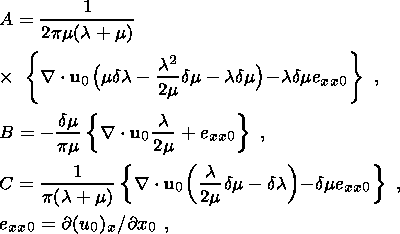
(52c) 6. Thermoelastic Deformation
6.1. Spectral Decomposition of the Solar Thermal Flux.
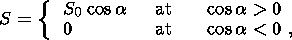
(53) 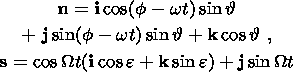
(54) 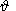 cos (Wt) cos e
cos (f - wt)
cos (Wt) cos e
cos (f - wt)
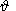 + sin (Wt)
sin
+ sin (Wt)
sin 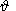 sin (f
- wt).
sin (f
- wt). 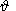 and
f are the colatitude and longitude, respectively;
W and
w are the angular frequencies of the orbital and
diurnal rotation of the Earth,
respectively; and
e=23.5o is the inclination angle
of the equatorial plane
with respect to ecliptic.
and
f are the colatitude and longitude, respectively;
W and
w are the angular frequencies of the orbital and
diurnal rotation of the Earth,
respectively; and
e=23.5o is the inclination angle
of the equatorial plane
with respect to ecliptic.
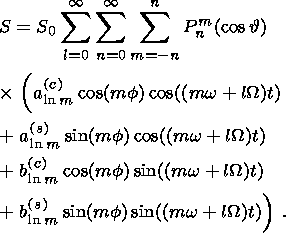
(55) 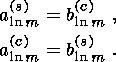
(56) 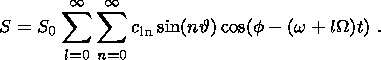
(57) 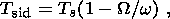
(58) 6.2. Equations of Thermoelastic Strains and Their Approximate
Solutions
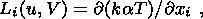
(59) 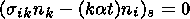
(60) 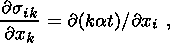
(61) 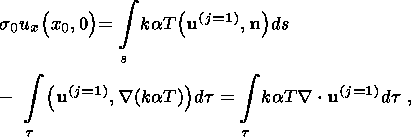
(62a) 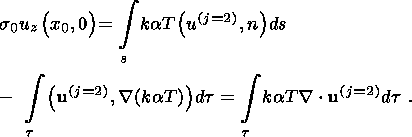
(62b) 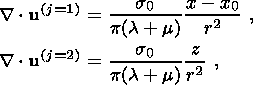
(63) 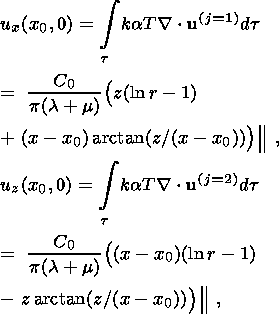
(64) 
(65)  T/
T/ t =
t = 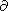 T/
T/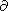 z2,
where
b is the ratio of the thermal conductivity of
the medium to its heat conduction, we have
z2,
where
b is the ratio of the thermal conductivity of
the medium to its heat conduction, we have
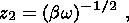
(66) 7. Numerical Modelling Examples
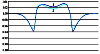
Figure 1
Figures 1
and 2
plot results of finite-difference modelling of tidal strain and
tilts for anomalous elastic moduli within a rectangular parallelepiped
( x1
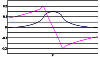
Figure 2
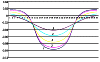
Figure 3
Figures 3
and 4
plot corrections to the
x components of linear strains (Figure 3) and tidal
tilts (Figure 4)
for an inhomogeneity specified within the unit cube ( -0.5
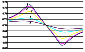
Figure 4
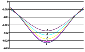
Figure 5
As an example of the application of relations (64)-(65), we consider possible
values of thermoelastic strains for the Protvino station
[Latynina and Boyarsky, 1999].
Analysis of long-term observations at this station indicates the presence
of well-pronounced seasonal variations in tidal strain amplitudes (the
K1 wave
amplitude in summer is higher than its winter value by about 40%). Such an
anomaly can be naturally accounted for by the presence of a thermoelastic strain
wave that has a sidereal-day period and an amplitude amounting to about 20% of
the
K1 amplitude and should coincide in phase with the tidal strain
variation
in summer. With these relations between amplitudes, frequencies and phases,
treatment of observation series a few months long fails to separate frequencies
of tidal and thermoelastic waves, but variations in the total amplitude reaching
40% of its average value should be clearly distinguishable.
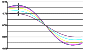
Figure 6
 0.2 m into (20) and taking
into
account geological evidence on the orientation of the Protvino station relative
to geodynamic zones separating blocks, we adopt the values
x1 = 500 m and
x2 = 1300 m for the respective distances from the tide-recording
station to the
near and far boundaries of the anomalous zones of orders 8-9. Then, the
thermoelastic strain value is
0.2 m into (20) and taking
into
account geological evidence on the orientation of the Protvino station relative
to geodynamic zones separating blocks, we adopt the values
x1 = 500 m and
x2 = 1300 m for the respective distances from the tide-recording
station to the
near and far boundaries of the anomalous zones of orders 8-9. Then, the
thermoelastic strain value is
 10-4 (aT0).
10-4 (aT0). 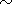 (10-5-10-4 ),
this strain amounts to
5
(10-5-10-4 ),
this strain amounts to
5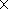 10-9-5
10-9-5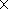 10-8,
which is comparable, on the order of magnitude, with the observed variations
in the amplitude of the tidal wave
K1.
10-8,
which is comparable, on the order of magnitude, with the observed variations
in the amplitude of the tidal wave
K1. Acknowledgments
This work was supported by the Russian Foundation for Basic Research, project no.
04-05-65117.
References
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on June 16, 2004.