Russian Journal of Earth Sciences
Vol. 6, No. 1, February 2004
Numerical analysis of geodynamic evolution of the Earth based on
a
thermochemical model of the mantle convection
L. I. Lobkovsky
P. P. Shirshov Institute of Oceanology, RAS
V. D. Kotelkin
Mechanical-Mathematical Faculty of the Moscow State University
Contents
Abstract
Full-scale numerical modeling of the geodynamic evolution of the Earth
throughout its existence is performed in terms of the thermochemical model of
mantle convection proposed by the authors. Numerical modelling results are
visualized in color and their detailed videorecord is presented. The global
geodynamic process is clearly characterized by the presence of cycles of
different lengths. Hydrodynamic pulsations associated with reorganizations of
convective cells in the upper mantle correlate well with the geological cycles
of Stille (~30 Myr). Moreover, the numerical experiments have shown that large
avalanche-like flows of substance from the upper mantle into the lower mantle
through their endothermic interface took place during the geodynamic evolution
of the Earth; these impulsive downward flows significantly differ both
quantitatively and qualitatively. In particular, impulsive flows of upper mantle
substance into the lower mantle on a continental or regional scale (the so-called
avalanches), also observable in our model, correspond in our
interpretation to the geological cycles of Bertrand (~170 Myr). In addition,
numerical experiments revealed the presence of basically new impulsive flows of
upper mantle substance into the lower mantle on a planetary (global) scale that
are referred to as overturns; about half of the upper mantle material is
replaced by the material of the lower mantle over a relatively short time of the
development of such an overturn. In our interpretation, the mantle overturns
correlate with the Wilson cycles (700-900 Myr), which is evidence of their
geodynamic nature and accounts for such major geological events as periodic
assemblages and breakups of continent, the asymmetric structure of the Earth,
and others. As the mantle cools during the evolution of the Earth, mantle
overturns gradually attenuate and degenerate into mantle avalanches.
Introduction
The mantle is the major layer of the Earth's structure and its physical state
and convective motions control contemporary geodynamic processes and their
effects in the past geological epochs. Therefore, their adequate description in
terms of mantle convection is of crucial importance for the evolution of the
planet as a whole.
A convenient mathematical approach to the separation of the mantle layer from
the global structure of the Earth and the separate examination of this layer
consists in the specification of fixed boundary conditions independent of
motions in the Earth's core. Since the Earth contains the metallic core with a
large heat capacity, whose outer part is in the liquid state and can freely mix,
convection in the mantle admits the classical formulation of the thermal
convection problem
[Rayleigh, 1916],
assuming that temperatures at the upper and
lower boundaries of the layer are constant and tangential stresses vanish at
these boundaries.
The classical approach has composed the independent, purely thermal direction of
research, whose main results were obtained by American and Canadian researchers
[Bercovici et al., 1989;
Glatzmaier et al., 1990;
Solheim and Peltier, 1994;
Tackley et al., 1993].
Original results obtained in terms of a thermal convection
model complemented with floating continents were obtained by Russian researchers
[Trubitsyn and Rykov, 1998, 2000].
Moreover, the classical approach provides a
theoretical basis for modern, more general models of mantle convection.
A priority in adopting the more general models belongs to the Russian scientific
school; these models, presently called thermochemical, take into account not
only thermal factors but also the mantle convection contribution of chemical
heterogeneity of the mantle. Significant analytical results concerning the
general models were obtained in the 1970s at the Mechanical-Mathematical
Faculty of the Moscow State University and were summarized in the monograph
[Myasnikov and Fadeev, 1980].
In particular, these studies provided a rigorous
asymptotic derivation of both equations and boundary conditions for a
thermochemical model including a boundary layer at the Earth's surface and a
core-mantle transition layer.
The Russian geophysical school has brought forward the concept of generation of
lighter mantle material due to its differentiation into metallic and nonmetallic
components in the core-mantle transition layer D

 [Artyushkov, 1979;
Sorokhtin and Ushakov, 1991].
According to these ideas, the differentiation in the D
[Artyushkov, 1979;
Sorokhtin and Ushakov, 1991].
According to these ideas, the differentiation in the D

 layer is due to melting with a rise in temperature and the descent of molten
iron-bearing components of mantle material into the core. The differentiation
effect on the mantle convection was studied numerically in
[Keondzhyan and Monin, 1980;
Monin et al., 1987].
layer is due to melting with a rise in temperature and the descent of molten
iron-bearing components of mantle material into the core. The differentiation
effect on the mantle convection was studied numerically in
[Keondzhyan and Monin, 1980;
Monin et al., 1987].
The second impulse to the development of the thermochemical convection concept
was given by new computer technologies of seismic data processing. Seismic
tomography of deep mantle layers
[Dziewonski and Woodhouse, 1987;
Fukao et al., 1994]
showed that the mantle contains large inclusions of heavy, supposedly
eclogitic material that have an important role in the convection process. A new
geological paradigm formulated in
[Maruyama, 1994]
is based on the predominant
role of heavy eclogitized masses in the development of mantle convection.
However, Maruyama did not verify his paradigm by numerical experiments, and
first fragmentary attempts at such modeling were made by
Christensen and Yuen [1984].
Thus, initial research of domestic scientists on the thermochemical models,
driven by the positive buoyancy force that arises at the core-mantle boundary
due to the differentiation processes taking place in its vicinity, was continued
by foreign researchers, although their approach was based on the predominant
role of the negative buoyancy force arising near the Earth's surface and
associated with the eclogitization of basic rocks of the oceanic crust. As was
noted at European conferences of the 1990s on mantle convection and lithospheric
dynamics
[Van Keken et al., 1997],
thermochemical modeling, involving a high
degree of resolution, requires much greater computer resources as compared with
purely thermal modeling, thereby largely limiting the possibilities of a 3-D
numerical simulation.
Numerical modeling provided a fundamental result of great significance for
mantle convection
Using new experimental data on the endothermic spinel-perovskite phase transition
[Ito et al., 1989, 1990]
fixing the upper/lower mantle boundary, F. Machetel and P. Weber discovered
an intermittent
pattern of mantle convection. This removed the basic contradiction between
geophysical data the whole-mantle convection scheme for their interpretation and
geochemical data that can only be interpreted in terms of convection developing
separately in the upper and lower mantle. Later, the intermittent pattern of
mantle convection was numerically reproduced by other researchers
[Solheim and Peltier, 1994;
Tackley et al., 1993],
who established that the exothermal
olivine-spinel phase transition at a depth of 410 km has an insignificant effect
on mantle convection.
Thus, it became clear that, in order to adequately describe mantle convection,
modern models should at least include the description of the endothermic phase
transition at the upper/lower mantle boundary.
In our work, we attempted to develop and analyze numerically a general
thermochemical model of mantle convection incorporating the aforementioned
positive and negative forces of chemical buoyancy and the endothermic phase
transition.
Since the reliability of inferred results is a critical point in numerical
modelling and the probability of numerical errors increases in the case of
multifunctional model, we developed and tested our model in several stages.
Taking into account the limitations of available computers and the complexity of
a mantle convection model incorporating the generation of both heavy and light
fractions and the phase transition, we chose a 2-D model of a specific geometry
minimizing movement restraints inevitable in the 2-D approach and, on the other
hand, simplifying the process of computations.
The traditional axisymmetric 2-D geometry evidently limits the convection
pattern to configurations inconsistent with the real geodynamic process and
involves a singularity (infinite coefficients) on the symmetry axis,
complicating the calculations and deteriorating the accuracy. These limitations
could be avoided by considering 2-D flows in the equatorial, rather than
meridional, plane.
Our initial calculations modelled the rise of light material to the surface under
conditions of thermal convection
[Lobkovsky and Kotelkin, 2000a].
Afterward, the endothermic phase transition was included into the purely thermal
convection model and, in order to test the model, we reproduced the intermittent
mantle convection in terms of axisymmetric geometry. Importantly, the test was
successful in relation to both the numerical algorithm and our specific 2-D model
geometry
[Lobkovsky and Kotelkin, 2000b].
Global thermal eclogitic convection calculated in
[Lobkovsky and Kotelkin, 2001]
was discussed qualitatively by Japanese authors on the basis of seismic
tomography data. These calculations adjusted, on the algorithmic level, the
mechanism of eclogite self-generation in lithosphere subduction zones controlled
by variations in hydrogeodynamic conditions; i.e. the processes of convection
and subduction of the basaltic oceanic crust were made self-consistent, so that
the origination and decay of subduction zones was directly controlled by the
process of evolution rather than by a priori artificial postulates of a
researcher. As a result, the modelling results agreed well with seismic
tomography data.
After these preliminary numerical experiments, we started analysis of the full-scale
process of mantle evolution in terms of our thermochemical model.
Experiments carried out for a
120o portion of the mantle layer
[Lobkovsky and Kotelkin, 2003]
demonstrated the possibility of numerical modeling of the mantle
evolution whose results are in good agreement with the geological evidence for
global cycles that existed throughout the evolution of the Earth. This paper
presents results of full-scale modeling of the Earth's evolution for the entire
annular layer of the mantle.
Mathematical Formulation of the Thermochemical Model
Notation
Variables:
t, time;
r, q and
j, spherical coordinates;
V = (Vr, Vq,
Vj), velocity;
Y, stream function for equatorial flows:
Vr= Y/r2
Y/r2 j, and
j, and
Vj=- Y/r
Y/r r;
r;
r, density;
p, pressure;
T, temperature;
C, concentration;
trq,
trj,
tjq,
and
tqq, viscous stress components;
D=E+2 /r
/r r and
E=
r and
E= 2/
2/ r2+
r2+  2/r2
2/r2 j2,
differential operators;
j2,
differential operators;
Constants:
er, unit vector;
r e, Earth's radius;
r c, radius of the Earth's core;
r0, average density;
g, gravitational acceleration;
a, thermal expansion coefficient;
k, thermal diffusivity;
cp, heat capacity;
h, effective viscosity;
Ch, Characteristic, generation rates of heavy and light fractions;
dr ecl,
density jump associated with eclogitization;
dr light,
density jump associated with "demetallization;''
Endothermic phase transition parameters:
dr ph,
phase transition density jump;
c(r - r ph), Heaviside
function;
r ph(j), phase transition boundary;
r pho = 0.875 (i.e. 670 km), reference
position of the phase boundary;
g, slope of the Clapeyron-Clausius phase curve;
h = g T ph
T ph dr ph/r20,
thermal effect of phase transition;
dr ph/r20,
thermal effect of phase transition;
Similarity criteria:
Ra =
r0 gaT0
r2 e/(hv0),
Rayleigh number
(the classical value Ra
1916 = RaPe);
Pe =
r ev0/k, Peclet
number;
f = dr
ph/dr
th;
G = gT0/(r0 g r e) = -dr
ph/dT ph;
H = gT ph dr ph/(r20
T0cp).
The mantle material is regarded as a weakly heterogeneous, highly viscous fluid
and is described in the Boussinesq and Stokes approximations; i.e. the medium is
considered incompressible and inertialess. The gravitational acceleration is
assumed to be constant in the mantle. The density is written as
r = r0
+ r ,
|r
,
|r |
|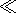 r0, p
= p0 + p
r0, p
= p0 + p ,
p0 = r0
,
p0 = r0 g
g (r e -
r),
(r e -
r),
where
p0 is the hydrostatic pressure. We also assume that displacements
at a
depth of 670 km and the phase boundary slope are small, so that, following
Boussinesq, they are approximately taken into account in equations of motion and
are neglected the heat conduction equation. In particular, the velocity
component normal to the phase boundary is approximated by the radial
component vr.
The mathematical model consists of the incompressibility condition and equations
of motion and heat-and-mass transfer, which in our approximation have the form
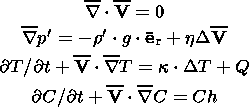 | (1) |
complemented by the relations
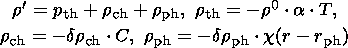 | (2) |
for the thermal, chemical and phase variations in density, respectively, and
Q = dc/dr  Vr
Vr  h/cp,
h = g
h/cp,
h = g T ph
T ph  dr ph/r20
dr ph/r20
for the heat generation during the endothermic phase transition.
The position of the phase transition is controlled by
p-T conditions. Setting
|p |
|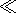 p0 at the phase transition depth yields
p ph
p0 at the phase transition depth yields
p ph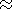 r0
r0
 g
g  (r e - r ph), so that
r ph = r ph0 - g
(r e - r ph), so that
r ph = r ph0 - g (T ph - T ph0).
The term
Ch describing the generation of the heavy and light fractions is
specified below at the stage of numerical calculations.
(T ph - T ph0).
The term
Ch describing the generation of the heavy and light fractions is
specified below at the stage of numerical calculations.
We introduce the following characteristic scales of the evolutionary process:
r e, v0, r0,
g, T0, a, k,
c p, h, g.
t0 = r e/v0, p0
= r0 gr e, r = r0
= r0
 a
a T0 = dr
th.
T0 = dr
th.
Then, taking into account relations (2), equations (1) can be written in the
following dimensionless form:
The similarity criteria are
Ra = r0 g aT0
r2 e/(hv0),
Pe = r e  v0/k, f = dr ph/dr th,
v0/k, f = dr ph/dr th,
G = gT0/(r0 g r e) = - dr
ph/dT ph, H = gT
ph dr
ph/(r20 T0cp).
In what follows, a more general definition of the Rayleigh number through an
arbitrary velocity scale is made for a convenient choice of the values
v0 and
t0; in this connection, we note the relation Ra
1916 = RaPe.
Boundary conditions are specified as follows:
r = r c: T = 1, vr = 0,
t = 0.
r = r e: T = 0, v r = 0, t = 0.
To examine the evolution of the mantle layer, initial distributions of
temperature and concentration should also be specified.
Formulation of the Model in an Equatorial Layer With
Conical Walls
Numerical experiments were conducted with the use of specific 2-D geometry. The
traditional axisymmetric 2-D approach has two drawbacks: first, axisymmetric
flows impose serious limitations on the convection pattern that are inconsistent
with the real process and, second, coefficients of such a model are infinite on
the symmetry axis, complicating calculations and deteriorating the their
accuracy.
In order to avoid these drawbacks, we consider, using the spherical coordinates
( r, q, j ),
an equatorial conical layer determined by the conditions
p/2 - d< q<p/2 + d
and assume that its conical boundaries
are adiabatic free-slip walls, i.e.
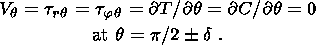 | (3) |
The, the model of 2-D equatorial flows, used in
[Lobkovsky and Kotelkin, 2000b],
are obtained through the passage to the limit
d 0. Since conditions
(3)
are specified on two walls, we obtain in the limit that the conditions
0. Since conditions
(3)
are specified on two walls, we obtain in the limit that the conditions
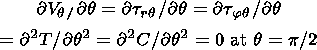 | (4) |
are also satisfied in the equatorial plane.
Now, in order to obtain the system of equations describing equatorial flows, it
is sufficient to write equations in the spherical coordinates ( r, q, j ),
set
q = p/2 and
take into account conditions (3)-(4). Note that, according to the
condition
 tjq/
tjq/ q = 0, the second derivative
q = 0, the second derivative
 2 Vj/
2 Vj/ q2
can be represented at
q = p/2 in
the form
q2
can be represented at
q = p/2 in
the form
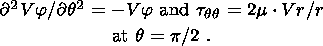 | (5) |
As a result, we obtain the system of equations
 Vr/
Vr/ r + 2 Vr/r +
r + 2 Vr/r +  Vj/
Vj/ j
= 0
j
= 0
 p/
p/ r = Ra
r = Ra  (T + C + f
(T + C + f c) + DVr
- 2 (
c) + DVr
- 2 ( V j/
V j/ j + Vr)/r2
j + Vr)/r2
 p/r
p/r j = DV f + 2 (
j = DV f + 2 ( V
r/
V
r/ j
- V j)/r2
j
- V j)/r2
 T/
T/ t + V r
t + V r 
 T/
T/ r + V
j
r + V
j
 T/r
T/r  j
= DT/ Pe + H
j
= DT/ Pe + H  d c/d r
d c/d r  T
T  V r
V r
 C/
C/ t + V r
t + V r 
 C/
C/ r + V
j
r + V
j
 C/r
C/r  j
= Ch,
j
= Ch,
which contains no singularities and is convenient for numerical modelling. Here
D is the Laplacian,
D = E + 2 /r
/r
 r, E =
r, E =  2/
2/ r2
+
r2
+  2/r2
2/r2  j2.
j2.
In accordance with the incompressibility condition, we introduce the stream
function
V r =  Y/r2
Y/r2
 j, Vj = -
j, Vj = -  Y/r
Y/r
 r.
r.
By differentiation, we eliminate pressure from the equations of motion and
obtain an equation for the stream function:
0 = Ra  (
( T/
T/ j
+
j
+  C/
C/ j + f
j + f G
G d c/d r
d c/d r 
 T/
T/ j)
j)
+ EE Y - 2  2
Y/r2
2
Y/r2  r2 + 4
r2 + 4  Y/r3
Y/r3  r
r
with the following boundary conditions:
at
r = r c, r e: Y
= 0 and
tr j
= 0, implying that
 2Y/
2Y/ r2 = 2
r2 = 2  Y/r
Y/r r. Applying the rule of the differentiation of a composite
function, we have
r. Applying the rule of the differentiation of a composite
function, we have
 c/
c/ j = d c/d
r ph
j = d c/d
r ph  d r
ph/d T ph
d r
ph/d T ph 
 T ph/
T ph/ j
j
= (- d c/dr)  (-G)
(-G) 
 T ph/
T ph/ j.
j.
A disadvantage of this model of equatorial flows is the impossibility of its
solution beyond the walls into the entire spherical layer of mantle. However, in
this case it is basically more important that the numerically modelled flows can
be realized in physical simulation models with small apex angles
d.
Numerical Implementation of the Model
In numerical implementation, the model differential equations were approximated,
within the second-order accuracy, by finite difference relations on meshes
regular in the coordinates
r and
j. The maximum size of meshes used in our
calculations amounted to 256
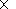 2048 cells covering the area ( 0.5
2048 cells covering the area ( 0.5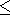 r
r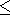 1;
0
1;
0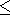 j
j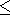 2p ), which yields a cell of the
size ( dr
2p ), which yields a cell of the
size ( dr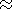 12 km;
d j
12 km;
d j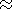 0,14o ). The
integration of the heat-and-mass transfer equations over time was also performed
within a second order of accuracy.
0,14o ). The
integration of the heat-and-mass transfer equations over time was also performed
within a second order of accuracy.
The concentrated force and heat generation associated with the phase transition
and described by the value
dc/dr were referred to the nondisturbed
position of
the phase boundary
r ph0 = 0.875 and were distributed (approximated) over
the
thickness of one mesh layer.
The generation of heavy and light fractions was also modelled at individual
nodes, i.e. was accurate to steps in space and time. Eclogites could only be
generated at depths of 80-100 km. Moreover, the generation of eclogites could
take place only at nodes that were adjacent to the subducting boundary of
convective cells ( Y = 0, Vr < 0 ) at the current time
moment. Under the
conditions mentioned above, the concentration at a node assumes the value
C ecl, and the further dynamics of eclogite is determined by the
heat-and-mass
transfer equation.
Generation of the lighter fraction can only occur at nodes adjacent to the lower
boundary of the model domain, where heavier iron-bearing fractions can sink into
the core. Moreover, the lighter fraction forms only if the temperature of the
cell at a current time moment exceeds the melting temperature
T melt, and in
this case the concentration assumes a value
C light.
Thus, the numerical model of the mantle is completely self-consistent: the
differentiation in the D

 layer is controlled by temperature, the number and
position of subduction zones is directly determined by the hydrodynamic
conditions in the upper mantle, and all processes, including the phase
transition, are interrelated through the velocity field.
layer is controlled by temperature, the number and
position of subduction zones is directly determined by the hydrodynamic
conditions in the upper mantle, and all processes, including the phase
transition, are interrelated through the velocity field.
The initial temperature distribution was taken in the form
t = 0; T(r) = 1 - exp [A  (r - 1)].
(r - 1)].
Choosing the value
A = 16, we obtain the initial distribution close to that
recommended in
[Vityazev, 1990].
Small initial perturbations causing the mantle to depart from the equilibrium
state were furnished by a small amount of light material (6%) uniformly
distributed throughout the mantle in a random manner. Eclogites are absent at
the initial time moment. The initial distribution of temperature and
concentration are shown in the first frame of the animated experiment (see also
Figure 2.0a below). Note that, in the inertialess approximation, the velocity
field is
determined at any (including initial) time moment by the temperature and
concentration distributions. With initial distributions specified in this way,
numerical experiments showed that 3- and 4-mode patterns of initial convection
(the initial number of ascending and descending flows, i.e. oceans and
continents) are most probable.
Many numerical experiments were carried out with various initial conditions,
model similarity criteria (Ra, Pe,
f, G and
H ) and parameters controlling the
chemical transformation rate
Ch.
The main goal of our study was to constrain the values of constitutive
parameters at which the thermochemical model of the Earth's global evolution
fits best the data of historical geology. The numerical experiments revealed the
presence of a relatively narrow range of values of constitutive parameters in
which the mantle evolution exhibits a well-expressed pattern involving a set of
different cycles; it is noteworthy that this range is consistent with the
available published data on physical properties of the mantle.
Temperature distributions were visualized on computer display in a natural color
palette convenient for perception; inclusions of eclogite and lighter material
are superimposed on the temperature distribution and their common dynamics is
animated. The results shown in this paper were obtained with the following
values of dimensionless parameters:
Ra = 5 104, Pe = 1300, f
= 2, G=-0.06, H = -0.035,
104, Pe = 1300, f
= 2, G=-0.06, H = -0.035,
C ecl=-0.3, T melt = 0.9, C light
= 1.0.
The corresponding dimensional values are
t0 = 1 Gyr, v0 = 0.7
cm/yr, T0 = 4000o C,
r0 = 4200 kg
m-3, g = 10 m s-2,
re = 6.4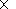 106
m, rc = 0.5
106
m, rc = 0.5 re;
re;
k = 10-6 m2
s-1, a = 1.4 10-5 1/o,
10-5 1/o,
cp = 1.25 103
J/( kg o);
103
J/( kg o);
dr th
= 200 kg m-3, dr ph = 400 kg m-3,
dr ecl
= 200 kg m-3, dr light = 600 kg
m-3;
h = 1022 kg
m-1 s-1 and g
= -4 MPa/o.
Results
|
|
Figure 1
|
With the aforementioned values of constitutive parameters,
the numerical
modelling results correlate remarkably well with main stages of the Earth's
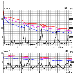
evolution. The main modelling result is presented in Figure 1, showing the
variation in the average velocity of the mantle, i.e. the convection activity
variation during 7.6-Gyr evolution (85000 time steps of integration), and
variations in the average temperatures of the upper, lower
and whole mantle,
which are the main consequences of the convective dynamics. Detailed
(nonaveraged) variations in temperature and concentrations of eclogite and
lighter material during 3.8 Gyr of the Earth's geological history is presented
in Animation 1,
as a video file, divided into four parts for its easier
examination via Internet. Figure 2 presents detailed distributions of
temperature and admixtures, as well as hydrodynamic patterns corresponding to
the key events of mantle history (peaks in Figure 1).
Figure 1
and the videorecord of the experiment show that the geodynamic process,
"launched'' from its unstable initial state 3.8 Gyr ago, reached a maximum
velocity of about 30 cm/yr, after which it rapidly attained the stable state
of
slow long-term evolution followed by global cycles, the first four of which
correlate well with geological data on the development of the Wilson cycles. In
agreement with the geological history
[Khain, 2001],
the numerical experiment yields an initial intense thermal wave coming from the planet's
interior followed by the long-term epoch of Archean evolution; the subsequent activity
pulse correlate with the existence and breakup of the first epi-Archean
continent in the period from 2.3 to 2.6 Ga; further pulses coincide in time
with
the second epi-Paleoproterozoic supercontinent existing from 1.65 to 1.4-1.35 Ga,
the third epi-Mesoproterozoic supercontinent Rodinia (1-0.8 Ga) and,
finally, the Wegener's Pangea (320-200 Ma).

|
|
Figure 2
|
The validity of such an interpretation of the dynamic evolution shown in Figure 1,
according to which outbursts of geodynamic activity play a key role in the
geological history of the Earth, becomes evident from analysis of the
videorecord of the experiment. Figure 2 presents fragments of virtual
hydrodynamic evolution of the Earth's mantle illustrating its characteristic
features. Compare the states of the mantle layer before (Figure 2a), during (Figure 2b)
and after (Figure 2c) an activity pulse responsible for a change in global
cycles. Fluid dynamics patterns are shown by streamlines at the bottom of Figure 2
(shades of yellow and green show clockwise and counterclockwise motions,
respectively, and the stream function is normalized to the current average
velocity), and the distributions of thermochemical heterogeneities for these
flow patterns are shown at the top.
Figure 2 (plate 2-0) shows the initial state of the mantle in accordance with
the
postulated post-accretionary state of the planet. This is a metastable thermal
state with uniformly distributed random inclusions of light material, with no
eclogite being present. The heterogeneities produce weak small-scale convection
evolving, in accordance with hydrodynamic laws, into rapidly growing (in the
given case, 4-mode) whole-mantle convection, leading to an abrupt mantle
overturn (an ideal overturn) characterized by velocities and surface heat fluxes
that are highest in the history of the Earth. As a result, the mantle passes
into a stable heterogeneous state, opening the long period of the Archean
evolution.
The post-Archean overturn (Figure 2.1), occurring in
a 2-mode regime and
characterized by smaller velocities, gives rise to asymmetry of the mantle
layer, so that subsequent overturns occur in a unimodal regime (Figures 2.2-2.4).
As seen from Figure 2, long intervals between geodynamic activity peaks are
characterized by relatively slow mantle flows with average velocities of 1-2 cm/yr
(see Figure 1)
in the regime of two-layer mantle convection, when heavier
and lighter heterogeneities accumulate on opposite sides of the phase boundary
(see Figure 02).
Several plumes and regional-scale subducting downflows are
observed in the upper and lower mantle.
However, the geodynamic activity outbursts, observable in
Figure 1a
as narrow
peaks of the average velocity of mantle flows reaching ~10 cm/yr (which is
typically three times lower than the maximum velocities), occur within the
framework of predominantly whole-mantle convection, as is evident from Figure 2b;
this regime exists usually (but not always) for a long time (Figure 1b).
Discussion
Examination and analysis of videorecords of numerous modelling experiments
provides insights into the origin and nature of the observed patterns. Note that
our model does not include the internal heating due to radioactive sources;
neither does it include the cooling of the Earth's core. This study examined the
mantle evolution from an initial state that is much hotter than its final state.
The mantle evolution proceeds in an impulsive, rather than quasi-stationary,
manner due to the presence of the endothermic barrier associated with the phase
transition at a depth of 670 km. The Wilson cycle essentially reduces to the
fact that, over a certain time of two-layer convection (the period of the Wilson
cycle), the thinner upper mantle cools first because its cooling surface is four
times larger than the heating surface of the lower mantle. If the cooling of the
upper mantle were uniform, the phase barrier would have been overcome
simultaneously throughout the boundary, resulting in a complete replacement of
the upper mantle material (an ideal overturn). The Bertrand cycles would have
been absent in this case.
The presence of lateral heterogeneities, first of all, accumulations of heavy
subducting material leads to "premature'' local flows of the phase barrier; yet,
due to an insufficient external energy supply, such flows cannot exist for a
long time and the homogeneity of the upper mantle is restored. The recurrence
rate of these events (Bertrand cycles) depends on the relation between the
height of the phase barrier and the accumulation rate of heavy material. Similar
processes of the accumulation of lighter material take place on the opposite
side of the phase boundary.
The evolution pattern is basically different, if a local flow through the phase
boundary occurs in the case of a cold upper and hot lower mantle. Vigorous
whole-mantle convection developing in this case rapidly replaces the cold upper
mantle material with the hot lower mantle material. Such mantle overturns differ
from "normal'' avalanches by considerable lateral displacements of mantle
material; indeed, before the heavy material of upper mantle will sink into the
lower mantle, it should be horizontally transported over a distance equal to
about one-fourth of the equator length. For this reason, overturns radically
change the Earth's face and are natural landmarks of the geological history. It
is unimodal overturns that are responsible for the asymmetric distribution of
continents and oceans. The average temperature of the upper mantle rises, over
the overturn time, by a few tens of degrees (by a few hundreds of degrees during
the earliest overturns), and the lower mantle temperature accordingly decreases.
However, the average temperature of the whole mantle is insensitive to both
overturns and avalanches, smoothly decreasing by an exponential law.
A factor having important implications for the appearance of mantle overturns is
the starting impulse initiating the convective process and determining its
behavior at the initial stage of the evolution (a few billion years). In the
experiment, illustrated above, such a concentrated starting impulse is ensured
by a post-accretionary planetary state uniform in the angular coordinate and
unstable in its radial component.
Numerical experiments show that mantle overturns (and Wilson cycles) degenerate
with time into avalanches, typically through the breakdown of a concentrated
pulse into a series of avalanches.
Between phase boundary breakthroughs, developed unsteady-state thermochemical
convection takes place in both upper and lower mantle, and its main events are
reorganizations of convective cells. Small cells unite to form larger ones,
which is well observable as convergence of subduction zones in the upper mantle
and as convergence of uprising plumes in the lower mantle. During such
convergence, flow velocities increase for a time, giving rise to small
pulsations superimposed on the averaged process; however, large cells rapidly
exhaust their feeding sources and break up into smaller and weaker cells, which
is clearly indicated by new subduction zones in the upper mantle. These events
regularly recur and should be associated with the Stille cycles. They are
primarily governed by hydrodynamic laws but are additionally enhanced by
eclogitization of the oceanic crust. Note that, along with the Stille cycles
observed at the Earth's surface, similar recurrent processes associated with the
development of plumes take place in the lower mantle.
Conclusion
We are well aware that the results, presented in this paper and obtained within
the framework of a rather simple model of the mantle, characterize only a
possible hypothetical variant of the real terrestrial process. Moreover, we
should note that the "convincing'' experiment described above is an exceptional
case among all experiments that we conducted. Due to the stochastic nature of
the process, the smallest changes in the modelling conditions shift peaks of the
resulting curve, worsening their agreement with the evidence of historical
geology; some peaks become diffused and degenerate into series of avalanches.
However, the experiment presented in this paper and our treatment of the Earth's
evolution reflect, on a statistical level, average tendencies of a large number
of experiments.
References
Artyushkov, E. V. (1979), Geodynamics,
320 pp., Nauka, Moscow.
Bercovici, D., G. Schubert, and
G. A. Glatzmaier (1989), Three-dimensional spherical models of
convection in the Earth's mantle, Science, 244, 950-955.
Christensen, U. R., and D. A. Yuen (1984), The interaction of a subducting lithospheric
slab with a chemical or phase boundary, J. Geophys. Res., 89, 4389-4402.
Dziewonski, A. M., and J. H. Woodhouse (1987), Global images of the Earth's interior,
Science, 236, 37-48.
Fukao, Y., S. Maruyama, M. Obayashi, and H. Inoue (1994), Geologic
implication of the
whole mantle
P wave tomography, J. Geol. Soc. Japan, 100(1), 4-23.
Glatzmaier, G., G. Schubert, and D. Bercovici (1990), Chaotic, subductionlike
downflows
in a spherical model of convection in the Earth's mantle, Nature, 347, 274-277.
Ito, E., and T. Takahashi (1989), Postspinel transformations in the system Mg
2 SiO
4 -Fe
2 SiO
4 and some geophysical implications, J. Geophys. Res., 94, 10,637-10,646.
Ito, E., M. Akaogi, L. Topor, and A. Navrotsky (1990), Negative pressure-temperature
slopes for reactions forming MgSiO perovskite calorimetry, Science, 249,
1275-1278.
Jeanloz, R., and A. B. Thompson (1983), Phase transitions and mantle discontinuities,
Rev. Geophys., 21, 51-74.
Keondzhyan, V. P., and A. S. Monin (1980), On the chemical convection in the Earth's
mantle, Dokl. Akad. Nauk SSSR (in Russian), 253(1), 78-81.
Khain, V.E. (2001), Large-scale cyclicity, its possible origins and general tendencies
of the Earth's tectonic history, in Fundamental Problems of General Tectonics
(in Russian),
pp. 403-424, Nauchnyi Mir, Moscow.
Lobkovsky, L. I., and V. D. Kotelkin (2000a), Geodynamics of mantle plumes, their
interaction with asthenosphere and lithosphere, and their effects on rifting and
trap formation, in General Problems of Tectonics: Tectonics of Russia (in
Russian),
pp. 304-308, GEOS, Moscow.
Lobkovsky, L. I., and V. D. Kotelkin (2000b), A two-layer thermochemical model of
mantle
convection and its geodynamic implications, in Problems of Global Geodynamics:
Proceedings of the OGGGGN RAN Theoretical Seminar of 1998-1999 (in Russian),
edited by D. V. Rundkvist,
pp. 29-53, GEOS, Moscow.
Lobkovsky, L. I., and V. D. Kotelkin (2001), Intermittent thermal eclogitic convection
in
mantle incorporating the 670-km phase transition and its comparison with data of
seismic tomography, in Tectonics of Neogea: Global and Regional Aspects (in
Russian),
pp. 378-381, GEOS, Moscow.
Lobkovsky, L. I., and V. D. Kotelkin (2003), Numerical modeling of the Earth's global
evolution during 4 Gyr in terms of a thermochemical model of mantle convection,
in Tectonics and Geodynamics of the Continental Lithosphere (in Russian),
pp. 352-357,
GEOS, Moscow.
Machetel, F., and P. Weber (1991), Intermittent layered convection in a model mantle
with an endothermic phase change at 670 km, Nature, 350, 55-57.
Maruyama, S. (1994), Plume tectonics, J. Geol. Soc. Japan, 100(1), 24-49.
Monin, A. S., D. G. Seidov, O. G. Sorokhtin, and Yu. O. Sorokhtin
(1987), Numerical
modeling of mantle convection, Dokl. Akad. Nauk SSSR (in Russian), 294(1),
58-63.
Monin, A. S., D. G. Seidov, O. G. Sorokhtin, and Yu. O. Sorokhtin
(1987), Numerical
modeling of mantle convection patterns, Dokl. Akad. Nauk SSSR (in Russian),
295(5), 1080-1083.
Myasnikov, V. P., and V. E. Fadeev (1980), Evolutionary Models of the Earth and
Terrestrial Planets (in Russian), VINITI, Moscow.
Solheim, L., and W. Peltier (1994), Avalanche effects in phase transition modulated
thermal convection: A model of Earth's mantle, J. Geophys. Res., 99(B4),
6997-7018.
Sorokhtin, O. G., and S. A. Ushakov (1991), Global evolution of the Earth,
446 pp., MSU, Moscow.
Tackley, P., D. Stevenson, G. Glatzmaier, and G. Schubert (1993), Effects
of an
endothermic phase transition at 670 km depth in a spherical model of convection
in the Earth's mantle, Nature, 361, 699-704.
Trubitsyn, V. P., and V. V. Rykov (1998), Three-dimensional spherical models of mantle
convection, continental drift, and formation and breakup of supercontinents,
Russian Journal of Earth Sciences, 1(2).
Trubitsyn, V. P., and V. V. Rykov (2000), Mantle convection with floating continents,
in
Problems of Global Geodynamics: Proceedings of the OGGGGN RAN Seminar of 1998-1999
(in Russian),
edited by D. V. Rundkvist, pp. 7-28, GEOS, Moscow.
Van Keken, P. E., S. D. King, H. Schmeling, U. R. Christensen, D. Neumeister,
and
M.-P. Doin (1997), A comparison of methods for the modeling of thermochemical
convection, J. Geophys. Res., 102(B10), 22,477-22,495.
Vityazev, A. V. (1990), Early Evolution of the Earth, Zemlya i Vselenaya
(in Russian), (2), 18-24.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on May 26, 2004.

 [Artyushkov, 1979;
Sorokhtin and Ushakov, 1991].
According to these ideas, the differentiation in the D
[Artyushkov, 1979;
Sorokhtin and Ushakov, 1991].
According to these ideas, the differentiation in the D

 layer is due to melting with a rise in temperature and the descent of molten
iron-bearing components of mantle material into the core. The differentiation
effect on the mantle convection was studied numerically in
[Keondzhyan and Monin, 1980;
Monin et al., 1987].
layer is due to melting with a rise in temperature and the descent of molten
iron-bearing components of mantle material into the core. The differentiation
effect on the mantle convection was studied numerically in
[Keondzhyan and Monin, 1980;
Monin et al., 1987].
 Y/r2
Y/r2 T ph
T ph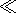 r0, p
= p0 + p
r0, p
= p0 + p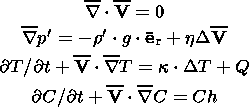
 r0
r0

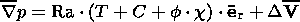
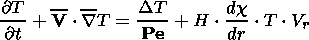
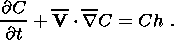
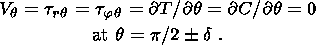
 0. Since conditions
(3)
are specified on two walls, we obtain in the limit that the conditions
0. Since conditions
(3)
are specified on two walls, we obtain in the limit that the conditions
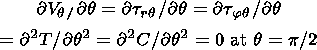
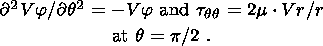
 2048 cells covering the area ( 0.5
2048 cells covering the area ( 0.5 r
r
