1. Introduction
The magnetic field and its secular variations ( SV ) observed on the Earth's surface are a complex function of space and time. The identification of regular patterns in the geomagnetic field relies not only on the acquisition of new experimental data but also on the application of more effective methods of analysis.
As was shown in [Astafyeva, 1996; Dremin et al., 2001; Dyakonov, 2002], the Fourier representation of a process and the application of the maximum entropy method [Cay and Marple, 1981] are ineffective for the analysis of processes with local features. This is due to the fact that the basis function inherent in these methods, being defined in the entire space, is a smooth and strictly periodic function. Such a function can provide constraints only on characteristic periods and intensity of their variations but not on the temporal localization and characteristic scales. The wavelet analysis [Daubechies, 1992; Mallat, 1989; Meyer, 1992] is free from these disadvantages. The wavelet transformation is based on the use of an essentially new basis (a wavelet) represented by a short wave with a zero mean and localized on the temporal (spatial) axis. Wavelets are constructed with the use of special basis functions enabling the representation of a 1-D process in the time-frequency (scale) plane and the analysis of its spectral properties as a function of time or scale.
Abroad, the use of wavelets dates back to the early 1990s. However, recently the interest in wavelets has sharply increased in Russia as well. Presently, a number of reviews have been published in Russian journals [Astafyeva, 1996; Dremin et al., 2001] and monographs devoted to wavelets have been translated [Chui, 2001; Daubechies, 2001]. Wavelets have also been widely used in geophysics [Alexandrescu et al., 1995; Alperovich and Zheludev, 1998; Gilbert et al., 1998; Ippolitov et al., 2001; Ivanov and Rotanova, 2000; Rotanova et al., 2002]. The goal of our work is to apply the wavelet analysis to the study of the temporal structure of the geomagnetic secular variations.
2. Method of Wavelet Analysis of Temporal Series
The wavelet transformation aims at the identification of the fine structure of a temporal or spatial series. In the general case, the family of analyzing wavelets is constructed in the form
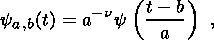 | (1) |
where a is the scale parameter, b is the shift parameter and n is the normalizing coefficient. Then, the continuous wavelet transformation of a discrete series fn(t) is defined as the convolution of this series with the wavelet y(a, b):
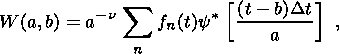 | (2) |
where y (a, b) is the basis wavelet function and the asterisk means a complex conjugation.
In our numerical calculations, we utilized the MHAT-wavelet [Rotanova et al., 2002], which has a narrow energy spectrum and two equal zero moments. The analytical expression for such a moment is
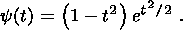 | (3) |
The wavelet transformation of the temporal series fn(t) yields a 2-D set of the coefficients W (a, b) providing constraints on the contributions of components of various scales and their variations with time. Based on the known values of W (a, b), it is easy to estimate some energy characteristics. Among the latter, the simplest and useful parameter is the energy density
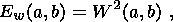 | (4) |
which characterizes the energy levels of the study process f (t) in the space (a, b).
Since an analogue of the Parseval equality exists for the wavelet transformation, the total energy of the process f (t) can be written, for real functions, through the amplitudes of this transformation as
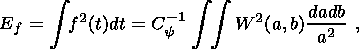 | (5) |
where C-1y is the normalizing coefficient similar to the coefficient in the Fourier transformation. The confidence interval of the energy spectrum of the wavelet transformation is determined as the probability that, at given parameters a and b, the true spectrum lies within the interval of the estimated wavelet power spectrum,
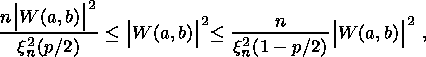 | (6) |
where |W (a, b)|2 is the true wavelet spectrum, n = N-1, N is the number of observation points, p is the significance level, and x2n (p/2) is the chi-square distribution with n degrees of freedom.
A series of estimates averaged along the shear parameter b or along the scale coefficient a. In the first case, we have the time-averaged power spectrum
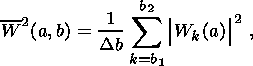 | (7) |
where Db = b2-b1+1 is the number of averaging points on the horizontal axis b. In the second case, the summation is performed over the scale axis a, and the scale-averaged spectrum has the form
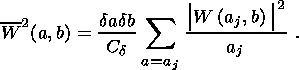 | (8) |
Since we examine the series varying with time, the wavelet coefficients are also time dependent. A natural measure for fluctuations of the coefficients is the variance distributions over various scales. The variance at each scale a is calculated by the formula
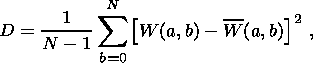 | (9) |
where N is the number of wavelet coefficients on a scale a in a given time interval.
The wavelet analysis is most suitable for studying the fractal behavior of a time series. This is due to the fact that the wavelet transformation provides a signal on various scales obtained by calculating the scalar product of the analyzing wavelet by the signal analyzed. As regards the wavelet coefficients, this implies the power-law behavior of their higher-order moments as a function of scale. The wavelet transformation allows one to calculated the higher-order moments Zq on various scales a:
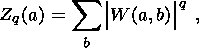 | (10) |
where maximum values of |W (a, b)| are summed. Dremin et al. [[2001] showed that, in the case of a fractal process, this sum should vary as
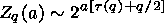 | (11) |
or
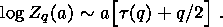 | (12) |
As follows from (12), the necessary condition for the self-similarity of the process is a linear dependence of log Zq on the scale a. If this condition is met, the dependence of the function t on the rank of the moment q defines the given process as mono- or multifractal. Monofractal processes have a single dimension, whereas multifractal processes are characterized by a set of such dimensions.
Finally, we dwell on a method for constructing the phase space portrayal and the attractor structure for the process studied. For this purpose, we make use of a procedure known in literature as the Takens procedure (in the theory of embedding of nonlinear dynamic systems [Takens, 1981]). This procedure reduces to the following.
Component vectors of the system state are constructed from the original temporal series SV(t):
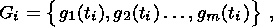 | (13) |
where gk (ti) = g[ti + (k + 1)l] and l is the retarding time. The spatial distribution of the vectors gm(ti) forms the reconstructed phase space of the dimension m.
3. Results Obtained from the Wavelet Analysis of the SV Temporal Series of the Geomagnetic Field

|
| Figure 1 |

|
| Figure 2 |

|
| Figure 3 |

|
| Figure 4 |
 40, after which it decreases monotonically.
Three features on the scales
a = 8-10,
a
40, after which it decreases monotonically.
Three features on the scales
a = 8-10,
a 20 and
a
20 and
a 40 are recognizable
in the curve
D(a). The variances
D
40 are recognizable
in the curve
D(a). The variances
D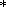 calculated
for
these scales with the averaging interval
Dt=10 years are shown in Figures 4b, 4c and
4d.
The resulting distributions are seen to be scale dependent. No singularities are
observed in the distributions
of
D
calculated
for
these scales with the averaging interval
Dt=10 years are shown in Figures 4b, 4c and
4d.
The resulting distributions are seen to be scale dependent. No singularities are
observed in the distributions
of
D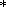 on larger scales (Figure 4b): the
variance increases until the 1940s, after which it decreases monotonically.
The histogram is more complicated on the scale
a=20 years: several variance extrema are observed,
and the
D
on larger scales (Figure 4b): the
variance increases until the 1940s, after which it decreases monotonically.
The histogram is more complicated on the scale
a=20 years: several variance extrema are observed,
and the
D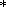 maximum
at the beginning of the century is followed by a decrease until 1930.
Particularly noteworthy is an abrupt decrease in the variance starting from 1950
and lasting until 2000;
however, two increase intervals of the variance are observed in 1970-1980 and 1990-2000
against the general
decreasing trend of
D
maximum
at the beginning of the century is followed by a decrease until 1930.
Particularly noteworthy is an abrupt decrease in the variance starting from 1950
and lasting until 2000;
however, two increase intervals of the variance are observed in 1970-1980 and 1990-2000
against the general
decreasing trend of
D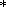 . The most interesting results
were obtained for the small values
a=8
. The most interesting results
were obtained for the small values
a=8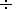 10 (Figure 4d).
10 (Figure 4d).
On these scales, fluctuations in the wavelet coefficients
and therefore in the variance are highest,
with maximum values of
D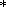 being observed in the 1970s
and 1990s. These years are of particular significance
from the standpoint of development of singularities. The distribution of the variance
of the initial
SV field
D,
shown in Figure 4e,
does not exhibit any anomalous behavior in the years mentioned above, thereby indicating
a dynamic origin of these phenomena. Thus, the temporal behavior of the variance
of the distribution of
wavelet coefficients shows that the scales 8-10 years are most sensitive to the development
of a singularity
in the
SVy field. It is possible that precisely these scales disturb
the linear behavior of the
sum
Zq as a function of the scale
a.
being observed in the 1970s
and 1990s. These years are of particular significance
from the standpoint of development of singularities. The distribution of the variance
of the initial
SV field
D,
shown in Figure 4e,
does not exhibit any anomalous behavior in the years mentioned above, thereby indicating
a dynamic origin of these phenomena. Thus, the temporal behavior of the variance
of the distribution of
wavelet coefficients shows that the scales 8-10 years are most sensitive to the development
of a singularity
in the
SVy field. It is possible that precisely these scales disturb
the linear behavior of the
sum
Zq as a function of the scale
a.

|
| Figure 5 |

|
| Figure 6 |
The plots presented in Figure 5 indicate that the
a dependence
of
log Zq is nonlinear, i.e., on the whole, the observed
process
SVy does not possess the property of
self-similarity (fractality). However, this dependence is linear for all values of
q at large
scales ( a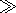 28
28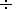 30 ).
Therefore, one can state that the process
SVy is fractal at large scales
a.
If this condition is met, the dependence of the function on the rank of moment
q (12) determines the
mono- or multifractality of the signal analyzed. We constructed
the dependences
t(q) for large scales
a,
and their examples for
a=30 and 40 are given in Figures 6a and 6b. Noteworthy are two features of these
plots: first, the function
t(q) is not strictly linear, which is evidence
of multifractality of
the process, and second, the functions
t(q) constructed for different scale values
virtually coincide.
For this reason, the function
t(q) can be considered as a scale-independent
measure of the fractal process.
30 ).
Therefore, one can state that the process
SVy is fractal at large scales
a.
If this condition is met, the dependence of the function on the rank of moment
q (12) determines the
mono- or multifractality of the signal analyzed. We constructed
the dependences
t(q) for large scales
a,
and their examples for
a=30 and 40 are given in Figures 6a and 6b. Noteworthy are two features of these
plots: first, the function
t(q) is not strictly linear, which is evidence
of multifractality of
the process, and second, the functions
t(q) constructed for different scale values
virtually coincide.
For this reason, the function
t(q) can be considered as a scale-independent
measure of the fractal process.
Returning to the results shown in Figure 5, we should note that all plots of the
a dependence of
log Zq reveal three different structures on the scales
a1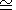 1
1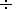 10,
a2
10,
a2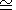 10
10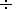 30 and
a3>30.
These structures appear to be due to different sources. The smaller scales can be
naturally related
to an external source, singularities of the jerk type from internal sources, and
noise. As regards the
larger scales, they are evidently related to internal sources.
30 and
a3>30.
These structures appear to be due to different sources. The smaller scales can be
naturally related
to an external source, singularities of the jerk type from internal sources, and
noise. As regards the
larger scales, they are evidently related to internal sources.

|
| Figure 7 |
|
| Figure 8 |
Thus, the results of wavelet analysis show that the SV temporal series are described by a process possessing a wide range of time scales. Apparently, this process is a superposition of several components: a stochastic low-frequency component, several regular variations with possible superimposed singularities, and irregular variations of the noise type.

|
| Figure 9 |
4. Possible Sources of Jerks
Presently, no theory has been developed for elucidating the origin of singularities on the Earth's surface. However, some hypotheses have long been proposed. Thus, in the opinion of Courtillot and Le Mouel [1988], a sharp variation is due to an abrupt change in the generation mode and is associated with additional movements in the upper part of the liquid core that arise in relation to a change in the rotation velocity of the inner part of the core. Possibly existing vertical movements in the liquid core known as upwellings [Voorhies, 1986] can either accelerate or decelerate the Earth's rotation, which should naturally have an effect on the SV generation. Runcorn [1985] believes that singularities in the geomagnetic field can arise due to instabilities in the toroidal field, whereas Hide [1985] regards such variations as a result of the interaction between Alfven waves in the liquid core.
Golovkov et al. [1996] obtained interesting numerical results for the interpretation of jerks in terms of the field of material velocities on the core surface. They showed that the leading mechanism of motions in the liquid core is provided by the rise and descent of material that are described the toroidal component of the velocity field. Vortex motions associated with the toroidal component should be regarded as a secondary effect of the vertical movements.
5. Induction Effects
Let the source of a sharp change in the SV field be the following model of a local disturbance:
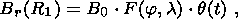 | (14) |
where q is a step function. In this case, the surface field variation should yield a peak the length and shape of which are determined by the conductive mantle.
We assume that
F (j, l)
describes a compensated source ( S Br dS=0 ) of a small spatial
size. After a signal of the chosen
geometry having a steplike time dependence passes through the conductive mantle,
the field
B (R0, t) on the Earth's
surface assumes the form consistent with the observed field variation pattern
[Braginsky and Fishman, 1977].
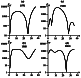
Such a theoretical dependence is sharply asymmetric and has a maximum. Near the epicenter,
the maximum is attained
over the time
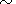 0.3t. As seen,
the role of the conductive mantle does not reduce to the delay of the signal by
a certain time (retarding time) and to the Gaussian smoothing of a certain width
(smoothing time).
The temporal dependence is strongly non-Gaussian.
0.3t. As seen,
the role of the conductive mantle does not reduce to the delay of the signal by
a certain time (retarding time) and to the Gaussian smoothing of a certain width
(smoothing time).
The temporal dependence is strongly non-Gaussian.
Characteristic slopes of the temporal dependence before and after the maximum are
different. Note that the observation
data possess the same properties. It is natural to estimate the mantle conductivity
from the characteristic increase
time because the post-maximum drop is masked by other smooth variations of the field.
The characteristic increase
time estimated from observation data is
t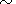 5 years. Hence, the screening parameter
is estimated at
t
5 years. Hence, the screening parameter
is estimated at
t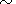 17 years,
which differs little from previous estimates of the screening and, accordingly, conductivity
[Braginsky and Fishman, 1977]
obtained from the analysis of local sources of 60- and 30-year variations amounting
to ~10
3 S/m at the core-mantle boundary
[Papitashvili et al., 1982].
17 years,
which differs little from previous estimates of the screening and, accordingly, conductivity
[Braginsky and Fishman, 1977]
obtained from the analysis of local sources of 60- and 30-year variations amounting
to ~10
3 S/m at the core-mantle boundary
[Papitashvili et al., 1982].
6. Conclusion
The main results of our study reduce to the following.
1. The wavelet analysis applied to SV temporal series of the last 100 years revealed singularities ~10 years long that were most intense in 1970 and 1990.
2. The field
SVy was subjected to the dispersion analysis based on the
results of wavelet transformations.
The analysis detected scales ( a = 8
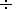 10) that are most sensitive to singularities in
the
SVy temporal series
and resolve best the singularities of 1970 and 1990.
10) that are most sensitive to singularities in
the
SVy temporal series
and resolve best the singularities of 1970 and 1990.
3. The results of the SVy wavelet transformation were used for calculating higher moments Zq; their estimates showed that the process analyzed does not possess the property of self-similarity (fractality). The process can be regarded as fractal only on large scales a.
4. The scale diagrams and the higher moments Zq obtained from the SVy wavelet analysis indicate the presence of three different structures depending on scale and most likely due to different sources.
5. The wavelet analysis results allowed us not only to identify singularities in the SVy field but also to trace variations in its energy parameters throughout the time interval studied.
6. The phase portrayal (attractor) constructed for
SV confirmed the complexity of the
SV structure.
The range of the dimension of the
SV dynamic system is estimated at
2
8. Based on analysis of the jerks, the characteristic time of screening of the
mantle was estimated
at
t
Alexandrescu, M., D. Gibert, G. Hulot, J.-L. Le Mouel, and G. Saracco,
Detection of geomagnetic jerks using wavelet
analysis, J. Geophys. Res., 100, 12,557-12,572, 1995.
Alexandrescu, M., D. Gibert, G. Hulot, J.-L. Le Mouel, and G. Saracco,
Worldwide wavelet analysis of geomagnetic
jerks, J. Geophys. Res., 101, 21,975-21,994, 1996.
Alperovich, L., and V. Zheludev, Wavelet transform as a tool for detection of geomagnetic
precursors of earthquakes,
Phys. Chem. Earth, 23, 965-967, 1998.
Astafyeva, N. M., The wavelet analysis: Theoretical fundamentals and application
examples (in Russian), Usp. Fiz. Nauk, 166, 1145-1170, 1996.
Braginsky, S. I., and V. M. Fishman, The 60-year geomagnetic field variations and
the electrical conductivity of
the mantle (in Russian), Geomagn. Aeron., 17, 921-926, 1977.
Cay, S. M., and S. L. Marple, Modern Methods of spectral analysis: A review (in Russian),
TIIER, 69, (11), 3-51, 1981.
Chui, K., Introduction to Wavelets (in Russian), Mir, Moscow, 2001.
Courtillot, V. E., and J.-L. Le-Mouel, Time variations of the Earth's magnetic field:
From daily to secular,
Annu. Rev. Earth Planet. Sci., 16, 389-476, 1988.
Daubechies, I., Ten Lectures on Wavelets (in Russian), RKhD, Moscow, 2001.
Daubechies, I., Ten lectures on wavelets, in CBMS Ser. Appl. Math. Soc. Ind.
Appl. Math. Pa., 61, Philadelphia, 1992.
De Michelis, P., L. Cafarella, and A. Meloni, A global analysis of the 1991
geomagnetic jerk, Geophys. J. Int., 143, 545-556, 2000.
Dremin, I. M., O. V. Ivanov, and V. A. Nechitailo, Wavelets and their applications
(in Russian), Usp. Fiz. Nauk, 171, (5), 465-501, 2001.
Ducruix, J., V. Courtillot, and J.-L. Le Mouel, The late 1960s secular impulse,
the eleven year magnetic variation and the electrical conductivity of the deep mantle,
Geophys. J. R. Astron. Soc., 61, 73-94, 1980.
Dyakonov, V. P., Wavelets: Theory and Applications (in Russian), Solon-R.,
Moscow, 2002.
Gilbert, D., M. Holschneider, and J.-L. Le Mouel, Wavelet analysis of the Chandler
wobble, J. Geophys. Res., 103, 27,069-27,089, 1998.
Golovkov, V. P., A. O. Simonyan, and S. V. Yakovleva, Calculation of the
velocity field at the Earth's core surface from data on geomagnetic jerks (in Russian),
Geomagn. Aeron., 36, 114-126, 1996.
Hide, R., A note on short term core-mantle coupling, geomagnetic secular variations
impulses, and potential magnetic field invariants as
Lagragian trancers of core motions, Phys. Earth Planet. Int., 39 (4), 297-300,
1985.
Ippolitov, I. I., M. V. Kabanov, and S. V. Loginov, Application of the
wavelet transformation to the analysis of yearly variations in the surface air temperature
in Omsk and solar activity (in Russian), Optika Atm. Okeana, 14, (4), 280-285,
2001.
Ivanov, V. V., and N. M. Rotanova, Wavelet analysis of a magnetic anomaly profile
obtained from MAGSAT data (in Russian), Geomagn. Aeron., 40, (2), 78-83,
2000.
Malin, S. R. C., B. M. Hodder, and D. R. Barrachlough, Geomagnetic secular
variations: A jerk in 1970, in Publicado on volumen conmemorative 75 aniversario
del observatorio del Ebro, pp. 239-256, 1983.
Mallat, S., A theory for multiresolution signal decomposition: the wavelet representation,
IEEE Pattern Anal. Machine Intell., 11, 674-693, 1989.
McLeod, M. C., On the geomagnetic jerks of 1969, J. Geophys. Res., 90, 4597-4610,
1985.
Meyer, Y., Wavelets and Operators, Cambridge Univ. Press, 1992.
Papitashvili, N. E., N. M. Rotanova, and V. M. Fishman, Estimating the
lower mantle conductivity from 60- and 30-year variations in the geomagnetic field
(in Russian), Geomagn. Aeron., 22, 1010-1015, 1982.
Rotanova, N. M., T. N. Bondar, and V. V. Ivanov, Temporal variations in
geomagnetic secular variations (in Russian), Geomagn. Aeron., 42, 708-720,
2002.
Runcorn, S. K., Geodynamic implications of short time scale changes in the geomagnetic
dynamo, Phys. Earth Planet. Int., 41, 73-77, 1985.
Takens, F., Lecture Notes in Mathematics, D. Rand and I.-S. Young,
Eds., Springer-Verlag, New York, 1981.
Voorhies, C. V., Steady flows at the top of Earth's core derived from geomagnetic
field models, J. Geophys. Res., 91, 1244-1266, 1986.
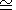 17 years,
which yields
sH.M.
17 years,
which yields
sH.M.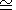 l.m. 10
3 S/m.
l.m. 10
3 S/m.
Acknowledgments
This work was supported by the INTAS Foundation, Grant No. 01-0142,
and the Russian Basic Research Foundation.
References
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on December 27, 2003.