Anisotropy of the rock drill core elastic properties at uniaxial loading

A. V. Patonin

The Borok Geophysical Observatory of the United Institute of Physics of the Earth, Russian Academy of Sciences

Contents

Abstract

Introduction

A reliably measured values of V_p and V_s will suffice for solving majority of the geological problems on the basis of the acoustic logging data to determine porosity factors and elastic characteristics of rocks. However, this is insufficient for a more detailed study of the dynamic behavior of the medium. A multiwave three-component exploration seismology and a multichannel acoustic logging permit to extend considerably the range of the geophysical problems such as: 1) clarification of the structural features of the section (low-amplitude dislocations with a break in continuity, pinching out etc.) from waves of different types; 2) study of the lithologic composition changes (argilization, lithologic replacement etc.) in the purposeful intervals of the section; 3) detection and localization of different lithologic composition in the sections, jointy intervals with separation of intervals which are characterized by a different jointing; 4) determination of the internal structure and parameters of the porous fractured space (jointing direction, porosity, cavernosity and jointing proportion, effective porosity etc.); 5) selecting the abnormal seam pressure zones in the section; 6) tracking the changes of nature of the porous fractured space in the course of using the deposits and fields, storages at monitoring conditions or at the hydraulic formation fracturing. Methods of detection and localization of anisotropic (fissured) intervals from the section as well as determination of their physical properties propose measurement of velocity of propagation and dynamic behavior (including polarization) of the longitudinal, converted and heteropolarized transverse waves in different directions in space [Erofeev, 2002].

Single-component piezoelectric transducers [Averko et al., 1967], mainly accelerometers and velocimeters, were used for a long time in the laboratory investigations for recording the acoustic emission signals. The wave length and the working frequency for the acoustic emission (AE) signals amounted to hundreds of kHz because of a small size of the tested sample. The recording proper must be of a three-component type to study polarization of the recorded waves in space. Reduction of components to be recorded to two or to one results in a loss of a great amount of information [Kozyar and Belokon', 2001].

The anisotropy of the section may be connected, as a rule, with a very thin bedding, clayiness or the rock jointing. Aside of this, a crystalline structure, granularity of the rock, air-filled pores in the magmatic rock have a great influence upon nature of the elastic properties. Jointing of the rocks in the field of natural stresses results in anisotropy of the geological properties and, consequently, to anisotropy of their elastic properties.

The anisotropy of elastic parameters of the rock may be assessed by the kinematics parameters (velocity of propagation of different type elastic waves) measured in different directions. It is possible to determine the anisotropy parameters such as the medium symmetry, anisotropy extent, orientation of the symmetry elements by measuring velocity of propagation of the longitudinal and heteropolarized transverse waves in different directions. It is possible to judge about structure of the porous jointy space (presence or absence of pores, cavities or joints, their quantity in the unit of volume, effective porosity, permeability etc.) and about orientation of the dominating system of joints in the given rock by parameters of the anisotropy.

The majority of the theoretical models of medium is based on a number of rather essential restrictions to simplify the numeric solution of the problem. These restrictions deal mainly with the boundary conditions and isotropy of the medium. The elastic properties of reservoirs, volume compressibility in particular, change depending on the nature of their saturation. Relation of the elastic components of the oil-water-saturated reservoir - rock skeleton, solid phase material and saturating fluids with the velocity of longitudinal and transverse waves is described by the known models of M. Biot [Biot, 1941] and F. Gassman [Gassman, 1951]. To determine the quantity oil saturation of reservoirs it is necessary to have a statistical connection of the oil saturation parameter with the oil saturation coefficient. This connection changes depending on the mineral composition and the lithologic structure of the rocks-collectors under investigation. The method for determining a complete dynamic compressibility by the time intervals of the longitudinal ( DT_p ) and transverse ( DT_s ) waves [Andreev and Krasavin, 1989; Dobrynin et al., 2002] is based on a precise measurement of the longitudinal and transverse wave velocity, porosity, density and clayiness of deposits under study. However, certain limitations are imposed on the materials under investigation: the porous body must be homogeneous and isotropic and the saturating phase must be continuous; the fluid saturating pores of the rock must have a final viscosity and compressibility; the most large (effective) pores of the reservoir are isolated hydraulically and no transfer of fluid is observed when the waves are passing through. At the same time, the real rocks are heterogeneous from the point of view of composition, porosity, grain size etc.

Experimental Technique and Equipment

Figure 1

The INOVA controllable electrohydraulic system manufactured in Czechia is the main instrument for the laboratory experiment. The INOVA system was developed specially for investigation of the rock materials at the supercritical loading stage. The maximum force at the uniaxial loading is 1000 kN. The program control allows to load the sample according to a specified condition using force or the piston travel or displacement as a parameter. Basically, loading at a constant rate of deformation is employed for the experiments. Accuracy of keeping the piston at a specified level is 0.5  m m. With this condition a linear displacement of the piston is set by a program. A proportional-integral-derivative controller (PID controller), with controllable control factors, controls position of the piston in compliance with the program. The control system allows to perform a fast load dropping (up to 0.01 sec) and the test is not carried to failure of the sample (Figure 1).

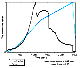
The time of the experiment is laid off along the X-axis. The normalized values of force and of the piston displacement are laid off along the Y-axis. A blue broken line shows the nature of the linear displacement of the piston at different rates of deformation. The initial loading step up to 1000 sec (a black curve) looks like normal, and afterwards a load break-down takes place because of the tensile crack intergrowing step-by-step during several experimental stages. In this case the load is not dropped completely. A further deformation of the sample leads to the increase of force. A gradual fracturing taking place in the sample and a further intergrowth of the crack which occurred earlier could be inferred by the nature of the curve. The sample looses the load-carrying capacity completely at the 1500 second. The tensile cracks have grown through completely and do not participate in the loading process. Despite the growing deformation the load does not increase but falls down, that is formation of numerous microcracks is taking place.

Figure 2

A 16-channel L-Card recording system was used to record the slowly changing physical parameters of the sample. The acoustic emission signals were recorded by a multichannel system manufactured by INSYS. The proprietary design 3-D piezoelectric transducers manufactured at the Borok Geophysical Observatory were used as transducers recording the acoustic emission signals. The design of the transducers assures a pass band from 0.5 Hz up to 300 kHz that allows to employ the transducers for solving a wide range of problems. With low values of the AE signal frequencies (up to 20-50 kHz) the transducers function as the displacement controllers. The velocimeters are employed for higher frequencies. The transducers ensure a point contact with the sample surface and at the same time the contact zone of all the three components is bounded by dimensions of 1.5 to 2 mm. The point contact and a small contact zone permit to obtain a wave pattern with minimum distortions (Figure 2) (components X, Y, Z for two transducers correspond to the blue, red and black colors).

A separate recording of the ultrasonic signal components allow to use the program packages and procedures for processing the 3-D seismic information. This enables the use of such parameters of the wave as velocity of propagation V, amplitude A, attenuation a, elastic wave energy E and that of the transverse wave S, Lamb L, Stoneley St [Belikov et al., 1970] to solve the geophysical problems.

The most important problems of the geophysical exploration seismology and of the multi-channel acoustic logging are as follows: 1) determination of the rock porosity factors from velocity of propagation (interval time Dt=1/v ) of the longitudinal wave P and, least often, of the transverse wave S; 2) determination of the elastic (dynamic) features of the rocks from the velocity of propagation of the P and S waves so as to find the rock drillability parameters, parameters of the hydraulic seam fractures, reservoir current oil saturation factors; 3) separation of the fissured rocks, including the hydraulic seam fracture propagation intervals, from attenuation (amplitudes) of the P, S and St waves, determination of direction of the rock anisotropy and of the preferred direction of cracks; 4) a direct separation (omitting determination of the porosity factors) of the permeable intervals by parameters ( V, A, E ) of the Stoneley wave [Koksharov, 1990]. Investigation of variation of anisotropic properties of the rock core sample during the uniaxial linear loading by a sonic test gives a better understanding of processes which are going on in a well. This allows also give a more precise and qualitative assessment of the above described parameters.

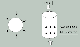
Figure 3

A limestone core 70 mm in diameter and 150 mm long was used as a sample in the experiment. Loading was on the controllable INOVA electrohydraulic system at a constant rate of deformation 2.0 E-5. The ultrasonic transducers of two types, arranged in groups on periphery of the sample some distance away from the base and equally spaced at 60^o. Standard piezoelectric accelerometers is one type of the transducers. The second group of transducers is the 3-D displacement transducers. Sounding was conducted by the emitters different in the frequency features. The sonic test was conducted along several different routes (Figure 3). The acoustic emission signals were registered at a maximum velocity of numbering 680 kHz per channel. Sounding of the sample along different routes was conducted at different loads with 1000 kg steps. The check measurements were made before loading and after the experiment.

Experimental Results

Figure 4

The loading curve shown in Figure 4 takes the form of a quadratic function. The volume dynamic compressibility index [Dobrynin et al., 2002] (red line) expresses a relative variation of volume with the rising load. The elasticity factor (broken black line) has several typical sharp bends in the region of 500, 800, 1250 and 1400 sec. Compression of the first level open cracks oriented along the normal to the axis of load takes place at the initial stage of loading up to 500 sec. Along with this components are compacted and mechanical clearances and backlash in the press-sample system are taken up. The dynamic compressibility index falls down and the elasticity factor is growing linearly. At the 500-800 sec. zone the sample comes to a linear rise of load depending on deformation. The volume dynamic compressibility index becomes constant and value of the elasticity factor also does not change. All pores which had opened earlier closed now and deformation of the sample skeleton takes place. At the same time the sample behaves as an elastic body. The nature of curves in the 800-1250 sec. zone is identical to curves of the initial loading stage. At this level the process of compaction and compression of pores and cracks of the second level occurs. In the 1250-1400 sec. zone the sample reaches the ultimate strength and the tensile joints begin to arise in the directions of the highest deformation tensor. The volume dynamic compressibility gradient curves and the elasticity factor change the sign. The inflection point characterizes the beginning of the sample flowage. At this moment the acoustic emission of the sample starts increasing sharply. Planes of the maximum deformation tend to a 45^o angle to the axis of loading. The tensile cracks occur at the same angle. The load keeps on rising, but at the same time the volume dynamic compressibility index increases sharply. At the 1700 sec. point an inflection on the loading curve is observed. At this moment formation of the tensile joints finishes. The sample quickly looses the load-carrying capacity. The process of shearing of the sample edges is going on and only the middle part of the sample remains intact. The press punch contact zone becomes narrow and the planes turn into a point. There is no sense to continue loading as the zones where the recording transducers were secured to have moved away from the main material and became on disconnected parts of the sample.

Wave Pattern on a Metallic Cylinder

Figure 5

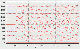
Figure 6

Figure 7

Before proceeding to measurement of the acoustic emission signals on the sample it is necessary to find out the nature of the wave pattern on an elastic isotropic body. We have taken a metallic pig of an adequate size to serve as the isotropic body. Ten 3-D transducers were placed on its periphery spaced at 36^o at the same distance from planes of the cylinder. The recording parameters were selected as for the work with the sample. Sounding was undergone without the axial load, in the center of the cylinder axis. The nature of the wave pattern separate from the X, Y, Z coordinates is shown in Figures 5, 6, 7. Numbering of the transducers is top-down.

The difference in moments of the wave arrival along X, Y and Z components taken together on all the 10 transducers was 1-2  m s that is equivalent to the longitudinal wave track length of 5 to 10 mm. The relative anisotropy of velocities is about 10%. This is a sufficiently great value for the material selected. This anisotropy value cannot be explained by a numbering error or by inaccurate attaching of transducers. The numbering frequency on one channel is equal to 681 kHz. Accuracy of attaching the transducers is 1 mm with the contact zone of 1 to 1.5 mm.

Figure 8

The distribution of the wave pattern on the sample was recorded in a similar way. The figure shows the distribution along coordinate Y only (Figure 8). The nature of the wave pattern along coordinates X and Z is similar and there are no phase distortions. However, the distribution of displacements along the coordinate Y shows typical preferred directions of movements. Numbering of transducers is top-down. Number of transducers is 6. Portions of the surface between transducers 1-2 and 3-4 oscillate out of phase. Direction of the oscillations is perpendicular to the axis of the sample. Directions of movements of the surface in the region of transducers 5-6 do not coincide with movement on transducers 1-4. Thus, it is possible to say that there is a certain boundary between transducers 1-4 and 5-6 the normal to which is along the line between transducers 2 and 3. The movement along axis Y is typical of the Stoneley wave which is formed in the near-surface layer. Polarization of the wave shows directions of the preferred orientation of microcracks and pores in the sample.

Sounding along different routes was made during the experiment for a more complete illustration of the wave pattern. Measurements were made at the loads of 0, 500, 1000, 2000, 3000, 4000, 5000, 5200 kg. The 5000 kg load is the value after which the force has been dropped down. This is the moment of formation of the main tensile crack. The drop of load at this time was 500 kg. The next measurement was at the load of 5200 kg immediately after the main crack has occurred.

Anisotropy of Velocities

Figure 9

Figure 9 shows an azimuthal distribution of the supersonic wave velocity obtained from the accelerometer data. The distribution is presented as diagrams. The first transducer on the diagrams is at the bottom and numbering is clockwise. The arrival time signal was determined from the first half-cycle of the wave crossing the maximum.

Figure 10

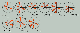
Figure 10 shows a similar distribution along the same routes but the transducers of another type were used. These were 3-D transducers. The criterion for assessing arrival of the wave was according to the first half-cycle of the wave crossing the maximum.

A comparative analysis of diagrams in Figures 9 and 10 shows that assessing of arrival of the wave according to the maximum of the first entry gives similar results which do not depend upon the type of transducers. One can say, however, that the 3-D transducers give a stable picture of distribution of velocities as assessment was along three directions at once.

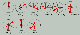
Figure 11

Figure 11 shows distribution of velocities obtained from the 3-D transducers but the moment of the wave arrival was determined according to the moment the signal began to appear. The beginning of the movement was accounted for along all the directions.

Figure 12

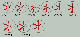
Diagrams in Figure 12 show distribution of velocities along the routes placed diagonally to the axis of load. A time difference of arrival of the signal to two adjacent transducers arranged on both sides of the axis of the route was determined for each route. Afterwards a total velocity was calculated for every 3-D transducer.

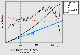
In this case the direction and nature of symmetry of the velocity anisotropy, as is shown in Figure 12, for the zero load before and after loading coincide fully. Only absolute lagging time increases from about 4 to 12  m s with the total travel time along the route about 40  m s. The initial step of loading 500 kg shows an increase of the anisotropy factor without any change of the direction. The portion of 1000-2000 kg can be characterized by a turn of the anisotropy vector. At first the factor diminishes and then it rises. The difference in directions of the anisotropy vector is 90% when compared with the results of the accelerometer measurements made at the same portion. At the 3000-4000 kg load portion the anisotropy vector turns toward the fifth transducer and the anisotropy factor reduces gradually. Just before the drop of load (the moment of the crack formation) the value of the anisotropy factor becomes the same as it was at the zero load. After the crack had been formed the anisotropy raised sharply and its directional diagram sharpened. The sample was unloaded, without carrying the test to the sample failure, and the anisotropy was measured once again. As has been mentioned before, the nature of the diagram after unloading is precisely the same as the diagram before the loading the sample. Therefore, it is possible to state with confidence that only weakening of the previously existed anisotropic zone has occurred in the sample and no essential change in the whole structure of the sample has taken place. A visual inspection of the sample surface after the load was been removed has shown that there were no visible cracks and shears on the surface. After completion of the experiment the sample was carried to failure for the purpose of revealing the main directions of the crack formation.

Figure 13

As can be seen in Figure 13, the main direction of the sample failure was along the diagonal to the axis of loading at about 30^o angle. A chipped off portion of the sample is divided into three parts. The contact sections of transducers 5 and 6 went to the shear zone. The direction perpendicular to the plane of shear passes between transducers 2 and 3. The direction of anisotropy presented in Figure 12 is in a good agreement with orientation of the crack which has been formed.

Conclusion

The comparative analysis of the supersonic wave velocities, obtained from the piezoelectric transducers of different types, allows to conclude that there are considerable limitations regarding the use of standard transducers. These limitations apply to heterogeneity of the material under investigation. With the maximum anisotropy (5-7%) measurements of the elastic wave velocities the transducers of different types present similar results. In the case when there is an abnormal lengthy zone in the material, the 3-D transducers a more accurate results. Diagrams of the azimuthal distribution of velocities obtained with the help of the 3-D transducers reflect the actual distribution in a better way. They present the actual picture of the elastic properties of the material more correctly and more properly. The procedure for determination of the elastic properties based on sonic testing of the sample along certain routes does not allow to draw correct conclusions if there is a different level jointing in the sample. The analysis of the wave patterns, obtained with the help of the 3-D transducers, has shown that polarization of the wave reflects orientation of the preferred jointing. It is necessary to employ both the amplitude and the phase characteristics of the signals to study the nature of porosity of the material. Of great importance is comparison of the results of measurement of the supersonic wave velocities with the values obtained by a direct calculation according to the loading curve for calculation of porosity of the oil saturated horizon. The type of the wave field changes rapidly in the course of loading because of a great number of the S-waves. A continuous monitoring of changes should be arranged to perform a quality analysis. Sections with different elastic properties are distinctly seen on the loading curve. The azimuthal anisotropy of the elastic properties of the rock does not permit to calculate with a sufficient confidence the porosity and oil saturation factors according to data of the multiwave acoustic logging. The study and analysis of samples by using the method of processing the multiwave acoustic data will allow to supplement the results obtained in field. The use of these procedures together with recording of all components of the wave package with the help of the 3-D transducers will permit to draw a more precise conclusion about nature of the elastic properties of materials.

References

Andreev, A. F., and S. V. Krasavin, Application of the Lamb waves for investigation of rocks in bore holes, Matters of technology of the geochemical and geophysical investigation during the exploration work and for the environmental control, pp. 28-35, VNIIgeoinformsistem, Moscow, 1989.

Averko, E. M., V. P. Golosov, and V. M. Kulikov, Procedure of simulation of the transverse waves, Transverse and converted waves in exploration seismology, Ed. Puzyrev N. N., pp. 146-155, Nedra, Moscow, 1967.

Belikov, B. P., K. S. Aleksandrov, and T. V. Fyzhova, Elastic properties of the rock-forming minerals and rocks, p. 274, Nauka, Moscow, 1970.

Biot, M. A., General theory of three dimensional consolidation, J. Appl. Phys., 12, 1941.

Dobrynin, V. M., A. V. Gorodnov, and V. M. Chernoglazov, Determination of oil saturation according to data on elastic properties of the oil and gas reservoirs, Materials on site: http://www.petrogloss.narod.ru/Dobrynin.htm, 2002.

Erofeev, V. I., V. V. Kazhaev, and N. P. Semerikova, Waves in spines, Dispersion, Dissipation, Non-linearity, pp. 21-45, Fizmatlit, Moscow, 2002.

Gassman, F., Uber die elastisitat poroser medien, Naturforschenden Gesellschaft Vierteljahrschrift, Zurich, (1), 96, 1951.

Koksharov, V. Z., The Lamb wave and its connection with permeability, Investigations on the multiwave acoustic logging and seismic simulation, pp. 3-12, IG and G Sib. Br. USSR Acad. Sci., Novosibirsk, 1990.

Kozyar, V. F., D. V. Belokon', and N. V. Kozyar, Progress and disadvantages of application of the acoustic logging, Directions in development of theory and practice for the nearest future, Transact. XI Session of RAS, Vol. 2, pp. 155-158, GEOS, Moscow, 2001.