V. A. Bol'shakov
M. V. Lomonosov Moscow State University, Geography
Department, Vorobyevy Gory, Moscow, 119992 Russia
Also at Geological Institute, Russian Academy of Sciences
Cyclicity is among the most all-embracing laws in Nature and Society [Atlas..., 1998]. Natural cycles come in a broad temporal range, from fractions of a second to billions of years. The cyclicity concept, rather than implying a strict periodicity, usually does involve a certain time interval required for the process in point to roughly repeat itself over and over again. Thus, the commonly known 11-year solar spots cycle includes time intervals of 5 to 16 years between solar activity peaks [Chistyakov, 1997], while the 100 thousand year (ka) cycle of the Earth orbit eccentricity variations consists mainly of harmonics approximating 95 and 124 ka [Berger, 1988]. It stands to reason that the shorter-period natural cycles, superposed on changes related to long-period cycles, may at least partly be governed by the latter. The well-known maxim, that studying the past helps to understand the present and to produce well-grounded forecasts of future developments, is therefore quite convincing. Resorting to this maxim in studying global climate changes in the Pleistocene implies that longer-period, 100-ka and 41-ka oscillations, forced by variations in the eccentricity and tilt angle of the Earth's axis of rotation, are superposed by 23-ka precessional oscillations that are variably modulated by longer period ones. Then, millennium-scale climate changes are superposed on 20-ka to 100-ka ones, and secular changes in turn modulate millennium-scale ones. Hence, global climate forecasting requires the knowledge of the nature and mechanism of the long-period climate changes in the Pleistocene. Unfortunately, this mechanism (which has to do, in particular, with the repeated global glaciation events of the last million years), despite the numerous allegations of its having been deciphered, remains as yet poorly understood. Let us dwell on previous studies dealing with this mechanism.
After the acknowledgment, in the first half of the 19th century, that glaciations are a phenomenon that recurred through the geologic past, the call for theoretical substantiation of this phenomenon became a pressing need. Proposed were numerous hypotheses, some invoking extraterrestrial factors. Thus, glaciation was attributed to (i) postulated changes in the solar constant, (ii) exposure of the Solar System, on its course around the Galaxy center, to space dust fluxes, (iii) considerably greater (than over the last million years) changes in the angle e between the Earth's equator and the ecliptic plane, and (iv) insolation changes forced by cyclic variations in the Earth's orbital elements. The last hypothesis just mentioned proved to be the most lucrative, eventually to win the widest popularity in accounting for global climate changes over the last million years, and it has been named the "astronomical theory of paleoclimate." However, because the other astronomical hypotheses have not altogether lost their potential as candidates for explaining the existence of glacial eras (such as, e.g., the Permo-Carboniferous glaciation), it would make more sense for a theory involving orbital forcing to be referred to as "an orbital theory of paleoclimate" (OTP).

|
| Figure 1 |
Unlike eccentricity variations, changes in the axial tilt (assuming the Earth to be spherical in shape) do not affect the insolation received by the whole Earth, merely redistributing this insolation across various latitudes. Hence, an increase in insolation at high latitudes (as the tilt angle e increases) will be counterbalanced by an insolation reduction at low latitudes, and vice versa, with the relative change in insolation at high latitudes being perceptibly stronger than at low latitudes. Insolation reduction at high latitudes will entail cooling and waxing of snow cover and ice sheets at these latitudes. This will increase albedo and further promote cooling (by positive feedback). Consequently, as Milankovitch [1939] was later to surmise, a drop in e would result in the Earth's cooling. Variations in the angle e are basically linked to cycles whose period is ca. 41 ka.
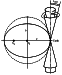
Precessional impact is mainly expressed in the changes in seasonal insolation contrasts between the different hemispheres. Provided that, while the Earth is at the aphelion, its Northern Hemispere faces the Sun (which is approximately the case during the current epoch), this particular hemisphere will have a relatively long cool summer, inasmuch as the distance from the Sun is longest and insolation is reduced. At the same time, the Southern Hemisphere will be the domain of a long cold winter. In half a year, as the Earth has moved to perihelion (the point of the Earth's orbit closest to the Sun), the Northern Hemisphere will become the site of a relatively moderate short winter, and the Southern, of a respectively warm short summer, because this time it will be the Southern Hemisphere to face the Sun at perihelion. In this case, seasonal climate contrasts are stronger in the Southern than in the Northern Hemisphere. In another 11.5 ka (a half period of climatic precession), as the Earth is at aphelion, it will be its Southern Hemisprere to face the Sun (Figure 1). Hence, the strongest climatic contrasts - i.e., long cold winters and short warm summers-will be observed in the Northern Hemisphere. Precession does not change the annual insolation received by the Earth. Furthermore, as was shown by d'Alambert as early as in the 18th century [Croll, 1875; Imbrie and Imbrie, 1988], the average annual change in the precessionally forced insolation is nil at any given latitude; i.e., the increased summer insolation is compensated for by the winter-time reduction in insolation and vice versa, at any given latitude. Evidently, the change in seasonal insolation contrasts decreases with eccentricity, so that with a circular orbit ( e = 0) precession will have no effect on the amplitude of the seasonal insolation contrasts, because the distance between the Earth and the Sun will remain constant. The mechanism of the precessional forcing of climate changes is understood least well. This will be detailed below, while at this point it should be noted that Croll [1875] believed that glaciation in a given hemisphere is triggered by climatic conditions involving extraordinarily cold long winters. Milankovitch [1939], on the contrary, thought that glaciation is promoted by climatic conditions with the longest and coolest summer half-years in the Northern Hemisphere. Apparently, both types of climatic conditions are materialized at the highest eccentricities.
The orbital theory of paleoclimate (OTP) was contributed to by many researchers, its most popular versions being those of Croll [1875] and Milankovitch [1939]. Milutin Milankovitch, an outstanding Yugoslav scientist, pioneered a mathematically rigorous calculation of changes in the solar radiation incident on the upper boundary of the Earth's atmosphere as a function of latitude, the time of the day, the season, and variations in the orbital elements. In the Northern Hemisphere, these irradiation changes for the summer caloric half-year, DQ s, and the winter caloric half-year, DQ w, are expressed as follows [Milankovitch, 1939]:
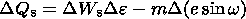 | (1) |
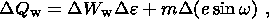 | (2) |
where DW is the latitude-dependent change in solar irradiation due to a change in the tilt of the Earth's axis De = 1o, m is a latitude-dependent coefficient, and w is the longitude of the Earth's perihelion relative to the Spring Equinox. (When considering the Southern Hemisphere, Formulas 1 and 2 should be interchanged, since, unlike tilt variations of the Earth's axis, governing in-phase insolation changes in both hemispheres alike, the precessionally forced half-year insolation changes occur in counterphase in the opposite hemispheres. The global signature of the precessional cycle is attributed to the dissimilarity between the hemispheres, with the Northern one being the focus of discussion because it is in this hemisphere that ice caps control the entire global glaciation in the Pleistocene). The above formulas, by the way, make it clear that, as mentioned above, annual irradiation changes at any given latitude due to precession (the sum total of the second summands in the right-hand parts of Formulas 1 and 2) are equal to zero.

|
| Figure 2 |
(1) The climatic cyclicity for the Brunhes chron is primarily governed by a 100,000 year periodicity, attributed to eccentricity variations, whose immediate impact is disregarded by the Milankovitch theory.
(2) The number of glacial events and their datings depart, by and large, from those for glacial events, as identified by Milankovitch using his insolation diagram, constructed for 65oN lat.
(3) Glacial events, according to empirical data, fall on eccentricity minima, whereas under the Milankovitch theory these are mainly coupled to eccentricity maxima.
(4) Global climate changes are synchronous in both hemispheres (at least as regards the peak of the last glaciation and the Holocene optimum), whereas the insolation curves calculated by Milankovitch for 65o S lat and 65o N lat yield misfits of at least 5,000 years in timing the insolation minimum and maximum (ca. 25 and 11 ka ago) coincident with these climatic events.
(5) About one million years ago, the dominant climatic periodicity switched from 41 ka to 100 ka, which is at odds with the Milankovitch theory, because the variation periods of orbital elements suffered no significant changes at that point in time.
It remains an enigma why, despite so many discrepancies between the Milankovitch theory and empirical evidence, it avoided being discarded, as the Croll theory did not (in due course and for similar reasons), and why its basic tenets were not even put to critical analysis. Such an analysis, performed quite recently by [Bol'shakov, 2000a, 2000b, 2001b], has revealed the following principal drawbacks of the Milankovitch theory:
(a) In determining the paleoclimatic significance of rigorously quantified insolation oscillations (which is the central achievement of the Milankovitch theory), related to variations of a set of orbital elements, Milankovitch disregarded the qualitative differences between these oscillations. It is meant here that eccentricity variations force changes in the annual mean heat inflow or, more exactly, in the amount of solar energy incoming to the whole Earth. However, the obliquity and precession variations virtually do not change the annual insolation received by the whole Earth, merely causing energy redistribution through latitudes and between the seasons, respectively, as mentioned above. These significant qualitative differences between insolation changes, forced by different orbital elements, were ignored in the Milankovitch theory. This circumstance alone suffices to discard the quantitative indices (calculated by Milankovitch in order to evaluate insolation changes) as being a realistic measure of global climatic impacts from variations in the respective orbital elements.
(b) The very technique of assessing the paleoclimatic significance of the variations in insolation incident on the upper boundary of the atmosphere, based on calculating these variations over particular caloric half-years and geographic latitudes, does not stand up under scrutiny. Indeed, one cannot reasonably assume that for a half-year insolation influences global climate, and for another half-year it does not. Likewise, it makes no sense to believe that insolation at a single given latitude governs global climate changes within the entire continuous and interrelated Earth climate system, whose inertia is enormous. The viability of this approach is further challenged by the fact already mentioned that half-year precessional variations in insolation, as well as insolation variations due to changes in the angle e at high and low latitudes, occur in counterphase. The spuriousness of this approach can be demonstrated clearly enough using the following case study. Take a metal rod with a high heat conductivity and a stabilized temperature. Let us increase heat supply to the ends of the rod, while equally reducing heat supply to its center, and then vice versa, thus simulating latitudinal heat redistribution due to a change in the axial tilt. It is readily apparent that the average temperature of the rod will remain unchanged throughout the experiment. Assuming that only the heat supply to the rod ends is taken into account (by analogy of how Milankovitch took into account insolation changes), the rod's average temperature must change (accordingly, rise or drop), which would be at variance with the reality.
This being so, precession-driven insolation changes can be presented (in a very simplistic form) as follows. Assume that the rod's average temperature is to be measured 12 hours after the last heating/cooling episode. Every second, the two halves of the rod are alternately heated or cooled in counterphase, with the amplitude of the heating/cooling cycles changing smoothly at a period of 12 hours. Clearly enough, in this case the change in the rod's temperature will be close to zero. If we take into account heat supply alone--e.g., the heat supplied every odd second and only to one half of the rod (by analogy of how Milankovitch calculated paleoclimatically significant precessionally forced insolation changes for the Northern summer caloric half-years)-then the temperature of the rod will change within certain limits, with the resultant growth of its average temperature. This change of the average temperature during the 12 hours (21,600 odd seconds) will follow the changes in the amplitude of oscillations in heat supply and, evidently, it will be much higher than in the corresponding real case, where the rod is being every second not only heated, but alternately also cooled virtually as strongly, with the heating of one half of the rod being synchronous to the cooling of the other half, and conversely.
Therefore, if one calculates insolation changes that are time-continuous (i.e., annual) and space-continuous (i.e., occurring at all the latitudes of the Earth), then the contribution to these changes from the axial tilt and precession will prove to be zero, because variations in these orbital elements, as mentioned above, do not change the annual insolation incident on the whole Earth. In this event, apparently, there are no grounds to create a theory linking global climate oscillations solely to the insolation changes governed by variations in obliquity and precession, inasmuch as these changes are zero. Not inconceivably, it was for these reasons that Milankovitch employed half-year insolation changes at individual latitudes for his paleoclimate interpretations. As was shown above, accounting for time- and space-continuous insolation changes is nonetheless prerequisite for constructing our theory in an adequate manner. Here it is worthwhile to recall the notable fact described by Schwarzbach [1955, p. 239] and related to the manner in which different researchers choose paleoclimatically significant insolation changes: "The first thing that catches your eye is the total mismatch between the Milankovitch and Spitaler curves. This is not because the authors used different eccentricity values, etc., which would have merely resulted in minor departures. The misfits are due to the fact that Spitaler divided the amount of radiation received at each parallel by the midday arc, and Milankovitch, by the midday plus midnight arc (because the midday and midnight arcs must be taken into account jointly [Wundt, 1944]). Hence, the two researchers obtained totally different amplitudes and, accordingly, different principal minima, which resulted in their obtaining dissimilar chronological divisions for the principal glaciation events. According to Wundt and other researchers, Spitaler's method is erroneous.'' This fact indicates that Milankovitch made a mistake similar to the one made by Spitaler, with the difference that he replaced Spitaler's midday insolation for the summer half-year one.
(c) Milankovitch, while calling his theory "...a strictly scientific mathematical theory of climate oscillations" [Milankovitch, 1939, p. 130], in its paleoclimate section made use of qualitative, rather than strictly mathematical, tenets. This applies to how he established the mechanism of climatic forcing from variations in the angle e and, especially, the mechanism of precessional forcing of climate. Recall that Milankovitch attributed paleoclimatic significance to insolation changes at 65o N lat, although doing without a rigorously grounded mathematical choice of this particular latitude. Note, however, that contributions to insolation variations from different orbital elements do depend on latitude, which influences the form of the insolation curve and, consequently, the timing of paleoclimate events portrayed by this curve (Figure 2). The relative change in the half-year precessional insolation at high latitudes is smaller than at low latitudes, whereas the relative insolation changes forced by obliquity variations are larger at high latitudes. Hence, the total half-year insolation change at low latitudes is governed by 23-ka precessional variations, and at high latitudes, by 41-ka variations in the Earth's axis tilt. The poor state-of-the-art in this sphere has resulted in that, subsequently, different researchers used insolation curves from different latitudes in order to substantiate interpretations of their own.
The starting point for constructing an orbital theory of paleoclimate and even for validating the pioneering hypothesis of orbitally forced insolation variations governing global climate changes is to create a physical mechanism for orbital forcing of climate variations. In establishing the mechanism for precession-forced climate changes, Milankovitch drew on Keppen's opinion [Imbrie and Imbrie, 1988; Milankovitch, 1939], according to which glaciation in a given hemisphere is triggered by climatic conditions involving long cool summers (and moderate short winters) - i.e., low seasonal contrasts of insolation. (Recall that this was at odds with Croll's [1875] opinion). In justifying his own mechanism, Keppen compared climatic conditions for cities situated at roughly the same latitude in Greenland (Gothåb) and in Eastern Siberia (Verkhoyansk and Yakutsk) [Schwarzbach, 1955]. The presence of glaciers in Greenland, which is typified by moderate winters and cool summers, and the lack of glaciers in Siberia, distinguished by severe winters, was assumed to validate the aforesaid causative mechanism (adopted by Milankovitch) for climate being influenced by precessionally forced insolation variations. This validation, however, is faulty, because the presence of glaciers, mild winters, and cool summers in the high-latitude Greenland is due to the immediate proximity of the Atlantic, which supplies moisture and snow to feed glaciers and moderates seasonal temperature oscillations. No such factor is available in Eastern Siberia. Nonetheless, despite the poor reasoning used to show that glaciation is chiefly triggered by seasons with long cool summers, this viewpoint is in circulation still [Cowie, 1984; Prokopenko et al., 2001; Ridgwell et al., 1999]. However, the reasoning employed to qualitatively explain the precessional forcing of climate, and usually attaching great importance not to the amount of ice produced during a cold winter, but to its amount surviving during a cool summer, is not very convincing. Let us use a case study of Cowie [1984] to try and demonstrate the above by comparing the data listed in Table 1. The left-hand column gives a quotation from [Cowie, 1984, p. 31] (option 1), while the right-hand one presents a mechanical rewording of this quotation, deliberately giving it an opposite meaning (option 2). The latter indicates that glaciation, on the contrary, is consistent with climate conditions with long cold winters. To my mind, this qualitative substantiation of the conditions making for ice waxing during periods of long cold winters is even more convincing than the one advanced by C. Cowie (especially considering the current climatic phase (interglacial)). The mechanism to explain the precessional forcing of global climate oscillations, which certainly does take place, is thus in need of a considerable refinement. The "dominant influence of seasonal insolation changes on global climate oscillations," an idea professed almost universally and borrowed repeatedly from publication to publication, cannot be found to agree with the reality because, besides other things, precessional changes are least well expressed in Pleistocene paleoclimatic curves.
(d) Another drawback is Milankovitch's failure to account for a set of diverse terrestrial feedbacks, or, more exactly, the fact that he accounted for them in a much less meticulous or mathematically rigorous manner (as compared to his calculation of insolation variations), and which he saw as being much less important than Croll did fifty years prior to him. Currently, the fact that feedbacks are prerequisite to transform weak insolation signals to global climate changes is commonly acknowledged. Moreover, some researchers [Oerlemans, 1980; Sergin and Sergin, 1969; Weertman, 1976] believe that there may exist independent, not forced by insolation, self-sustained oscillatory global climatic processes governed by feedbacks through interactions in the system ocean-land-atmosphere-cryosphere. Let us use a concrete case study to demonstrate how important it is to take feedbacks into account. In validating the mechanism of the climate impact from variations in the Earth's tilt (a decrease in e causes a decrease in insolation at high latitudes, thus resulting in cooling), Milankovitch used a positive feedback mechanism controlled by a change in albedo due to an areal change in the ice and snow cover, mainly at high latitudes. However, because during e variations, insolation changes occur in counterphase at high and low latitudes, the existence at low latitudes of a positive feedback that could be comparable to the high-latitude "albedo'' feedback would strongly obstruct the unraveling of how variations in the angle e influence climate.
This example shows that accounting for the character of feedbacks may help to solve the problem of the precession- and obliquity-related insolation variations having a zero annual mean for the Earth as a whole and to establish the global climate significance of these variations. It is common knowledge that there exist other terrestrial feedbacks, some of these being not only positive (due to albedo changes following changes in the volume of ice and snow and in the vegetation cover of the planet or changes in the atmospheric content of greenhouse gases), but also negative, e.g., due to invigoration of circulation in the atmosphere and hydrosphere, tending to reduce the longitudinal temperature gradients, which increase during glaciation events. There are good reasons to assume that these types of feedbacks exert different influences on orbital signals caused by variations in individual orbital elements. Thus, the positive feedback controlled by albedo changes (primarily at high latitudes of the Earth) will most likely provide the strongest amplification for the insolation signal due to variations in the axial tilt, whose largest relative changes are also restricted to high latitudes. The feedback induced by oscillations in the atmospheric contents of greenhouse gases is most likely to exert the strongest influence on the immediate (not connected with precessional modulation) eccentricity signal, changing the annual mean insolation of the entire Earth. Changes in the rate of atmospheric and hydrospheric circulation, involving changes in temperature gradients, would likely exert a comparable influence on insolation signals related to variations in either of the two orbital elements. The less well understood mechanism for precessional influence on climate, associated, in particular, with paleomonsoons [Barron et al., 1985; Clemens and Prell, 1991; Prell and Kutzbach, 1987; Rossignol-Strick, 1983], may have a regional rather than a wider significance, and, hence, it can exert its specific influence through terrestrial feedbacks on the paleoclimatic precessional signal.
Therefore, the existence of linear amplification of insolation signals, postulated by the Milankovitch theory, is not grounded well enough. This is further evidenced by the fact that Milankovitch's followers had to adopt, to be consistent with empirical data, the "non-linear amplification'' mechanism for the eccentricity-induced insolation signal [Berger, 1988; Hays et al., 1976; Imbrie et al., 1984, 1993]. Furthermore, contrary to these authors' belief, the same set of empirical data suggest that those insolation changes due to variations in the axial tilt and precession involve no linear amplification. Thus, the insolation curve of Berger [1988] for 65o N lat show the dominant contribution to be from precession, whereas the 41-ka component, attributed to the axial tilt, prevails over the 23-ka one in the paleoclimate record of d 18O variations.
This is the reason why a due account of feedbacks (that influence, in a number of ways, the insolation signals correlative to variations in the individual orbital elements and exerting an appreciable influence on the real climatic significance of these elements) may change considerably the insolation diagram of Milankovitch, which he interpreted as being a paleoclimatic curve. A rigorous account for a variety of feedbacks is thus among the pivotal prerequisites for constructing an adequate paleoclimate curve and, accordingly, an orbital theory of paleoclimate. It is precisely by taking into account how these feedbacks operate through time and space that one can solve the problem of zero annual mean insolation changes (related to variations in the tilt angle and precession) over the entire Globe. This would require developing a realistic and accurate mechanism for climatic influences from variations in a set of orbital elements, primarily precession.
It is relevant to present here an appraisal of the theoretical climatic section of the Milankovitch theory (dedicated to calculating one of the principal climate indicators, temperature), as formulated by prominent expert in climate theory Academician Budyko [1977, pp. 84-85]: "Milankovitch believed that thermal regime is determined by radiation heat exchange in each particular latitude zone. His work disregarded the influence of the atmospheric greenhouse effect and albedo changes with latitude. Milankovitch also ignored the effect exerted by meridional heat transfer in the atmosphere on thermal regime, heat exchange due to water phase transformations, and interaction between the atmosphere and the ocean. The significant errors in calculating the temperature field due to the influence of these factors, were compensated for by adjusting certain model parameters, thus enabling Milankovitch to obtain a distribution of mean latitude temperatures that differs not very strongly from the one actually observed. This adjustment, however, was rather arbitrary.'' This particular section of the Milankovitch theory was also criticized by [Kominz and Pisias, 1979; Shaw and Donn, 1968]. Needless to say, criticism of the theoretical estimates of temperature changes refers not only to Milankovitch personally, but also to the overall 1930s scientific level. In particular, as we could see above, some meteorologists and climatologists of that time did not view the availability of a sufficient amount of moisture as being critical to triggering glaciation.
Obtaining a rigorously calculated paleoclimate curve consistent with empirical data would in fact signify completion of the construction of the orbital theory of paleoclimate. This implies establishing (in an adequate way) mechanisms responsible for global paleoclimate changes - i.e., primarily, identifying the most important feedbacks and concrete mechanisms that encompass the interplay of the atmosphere, hydrosphere, cryosphere, and lithosphere, and that transform orbitally forced insolation variations to global climate changes. It is only on the basis of such a theory that one may expect correct results to be obtained in forecasting natural, "background,'' global climate changes, modulated by anthropogenic impact on the natural environment.
Currently, we are far from having solved this problem. As was shown above, the Milankovitch theory, accepted almost universally as being an analogue to the orbital (astronomical) theory of paleoclimate, shows essential departures from empirical data. Furthermore, this theory has considerable drawbacks, precluding the viewpoint that the Milankovitch insolation diagram has not a global climatic significance. Milankovitch's error in accounting for time-discrete summer insolation caloric half-years is merely being further aggravated by his followers [Berger and Loutre, 1991; Laskar et al., 1993] by calculating monthly and even daily insolations. The insolation curves thus obtained, devoid of any paleoclimatic significance, are used for paleoclimate modeling [Berger, 1999; Berger et al., 1998; Imbrie and Imbrie, 1980], whose results barely demonstrate the great potential of mathematical methods in obtaining virtually any sort of conclusion. However, as was justly noted by Berger [1999], these results lack solid physical substantiation.
The above also suggests the lack of grounds for introducing the notion of a mechanism for "non-linear" amplification of the eccentricity signal. This conclusion follows primarily from the fact that insolation signals coupled to individual orbital elements have qualitatively different structures - i.e., their changes through time and space (annual and seasonal totals for the whole Earth and for individual latitudes) follow different patterns. On the contrary, from this standpoint one may interpret, say, the amplification of a precessional or insolation signal (which equals zero for any given latitude, provided its annual mean has been calculated) as being non-linear. Because the focus of our study is global climate oscillations with periodicities of several tens of thousand years, a precessional signal that equals zero on such long time scales and for the Earth as a whole does require a singular, "non-linear" amplification mechanism. Eccentricity changes, by contrast, govern small insolation changes that are non-zero on an annual scale and for the entire Earth; consequently, an eccentricity signal can be transformed to global changes (albeit with a very large amplification coefficient) through a linear mechanism. On the other hand, as was shown above, different feedbacks have different ways of interacting with insolation signals from individual orbital elements. Hence, generally speaking, transformation of weak insolation signals, linked to any given orbital element, to global climate changes may in each particular case be viewed as being due to a non-linear amplification mechanism. However, the main purpose of such a consideration is not to stick a label, but to pinpoint this particular concrete mechanism and the conditions required for its implementation.
Currently, there exist a multitude of explanations for a number of challenging issues of the orbital theory of paleoclimate, such as the issue of the 100-ka climate period and other empirically established non-orbital periods [Berger, 1988; Clements and Prell, 1991; Hays et al., 1976; Pisias and Rea, 1988; Wigley, 1976], the issue of the Middle Pleistocene transition, etc. (see the synopsis by [Elkibbi and Rial, 2001]). To my mind, the principal flaw shared by many of the models is also the lack of a concrete physical mechanism explaining one or another phenomenon, as well as the overall pattern of climate changes in the Pleistocene. (This is especially true of those models making use of the relationships between orbital frequencies in order to explain the emergence of new climatic periods--e.g., when the difference between the inverse periods (frequencies) of the precessional harmonics is equal to the inverse period of the eccentricity harmonic). In particular, no explanation is usually provided for the coincidence of the glacial events of the last million years with eccentricity minima or of the interglacial events with eccentricity maxima.
Hence, it can be concluded that there is no realistic, strictly theoretical validation for the orbital theory (hypothesis) of paleoclimate. The only piece of evidence definitely in favor of this hypothesis is the empirically obtained result on the similarity of periods of paleoclimatic changes and orbital periods. Nonetheless, even this is no direct evidence that orbitally forced insolation variations exert a dominant influence on global climate changes. Thus, Jupiter's period of revolution around the Sun (11.9 years) is close to the 11-year average period of solar activity changes. But this does not imply automatically that changes in the number of solar spots are caused by Jupiter's revolutions. For this reason, constructing a rigorous orbital theory of paleoclimate requires primarily a clear, physically validated mechanism for cause-and-effect links between variations in the Earth's orbital elements (that cause the corresponding insolation changes) and global climate oscillations. A pivotal support for such a mechanism could be provided by a paleoclimate curve consistent with empirical data and constructed on the basis of theoretical tenets deduced while developing this mechanism, and this is exactly what Milankovitch tried to do. However, as was shown above, a precise solution to the problem of calculating a paleoclimate curve requires that time- and space-continuous insolation changes, related to variations in all three orbital elements, be taken into account, while concomitantly accounting for the variety of terrestrial feedbacks, operating both regionwide and on the global scale alike. It is clear that solving this breathtaking problem and, not inconceivably, the very possibility of its precise solution, is the competence of paleoclimate modeling experts. Hence, for constructing a paleoclimate curve similar to the Milankovitch insolation diagram, [Bolshakov, 2000a, 2000b, 2000c] proposed a simplified and rather generalized approach.

|
| Figure 3 |
|
| Figure 4 |

|
| Figure 5 |
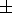 1 on the ordinate axis, with negative values, as
agreed initially,
corresponding to cooling events. Then, the normalized variations in each particular
orbital element were each
attributed a distinctive climatic significance coefficient. This was performed in
compliance with empirical
paleoclimate data, which suggested that different periods of climate changes had
different amplitudes
(intensities) of these changes. The most marked climate changes of the last million
years have a periodicity of
ca. 100 ka, which is ascribed to eccentricity variations. This is the reason
why the largest climatic significance
coefficient, equal to 1, was adopted for the eccentricity curve. Climatic significance
coefficients for the other
two orbital elements were found by trial-and-error so as to
achieve the best fit between the resultant integrated
curve and those available trustworthy oxygen isotope (OI) curves that have a sufficient
resolving power, and
which currently provide the most reliable records of global climate changes. These
coefficients proved to be
0.7 for
e and 0.4-0.55 for ( -e sinw).
The integrated curve thus obtained (Figures 4 and 5),
called the "orbital climate diagram'' (OC diagram)
[Bol'shakov, 2000c; 2001a, 2001b],
represents an expected climatic effect from
insolation variations related to all three orbital elements, or, in other words,
the conventional relative
probability
DP of cooling (for negative
DP ) and warming (for positive
DP ).
We interpret the deepest
DP minima as being coincident with the most
probable glaciation events. The best fit between the
glaciations oxygen isotope
curve and the OC diagram is achieved at
DP
1 on the ordinate axis, with negative values, as
agreed initially,
corresponding to cooling events. Then, the normalized variations in each particular
orbital element were each
attributed a distinctive climatic significance coefficient. This was performed in
compliance with empirical
paleoclimate data, which suggested that different periods of climate changes had
different amplitudes
(intensities) of these changes. The most marked climate changes of the last million
years have a periodicity of
ca. 100 ka, which is ascribed to eccentricity variations. This is the reason
why the largest climatic significance
coefficient, equal to 1, was adopted for the eccentricity curve. Climatic significance
coefficients for the other
two orbital elements were found by trial-and-error so as to
achieve the best fit between the resultant integrated
curve and those available trustworthy oxygen isotope (OI) curves that have a sufficient
resolving power, and
which currently provide the most reliable records of global climate changes. These
coefficients proved to be
0.7 for
e and 0.4-0.55 for ( -e sinw).
The integrated curve thus obtained (Figures 4 and 5),
called the "orbital climate diagram'' (OC diagram)
[Bol'shakov, 2000c; 2001a, 2001b],
represents an expected climatic effect from
insolation variations related to all three orbital elements, or, in other words,
the conventional relative
probability
DP of cooling (for negative
DP ) and warming (for positive
DP ).
We interpret the deepest
DP minima as being coincident with the most
probable glaciation events. The best fit between the
glaciations oxygen isotope
curve and the OC diagram is achieved at
DP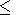 - 0.5
(Figures 4
and 5).
Note that the OC diagram is, by and large, a
theoretically constructed diagram, inasmuch as its creation draws on (a) the
general theoretical mechanisms of
global climate effects of variations in orbital elements, (b) theoretical calculations
of these variations
[Berger and Loutre, 1991],
and (c) the theoretically validated possibility that the climatic significance
coefficients
attributed to the variations in individual orbital elements are interrelated in a
different way than in the
Milankovitch theory.
- 0.5
(Figures 4
and 5).
Note that the OC diagram is, by and large, a
theoretically constructed diagram, inasmuch as its creation draws on (a) the
general theoretical mechanisms of
global climate effects of variations in orbital elements, (b) theoretical calculations
of these variations
[Berger and Loutre, 1991],
and (c) the theoretically validated possibility that the climatic significance
coefficients
attributed to the variations in individual orbital elements are interrelated in a
different way than in the
Milankovitch theory.
A diagram resembling the OC diagram was constructed earlier [Imbrie et al., 1984]. It was called ETP, because it integrated normalized variations in eccentricity (E), Earth axial tilt (T), and precession (P). Therefore, formally, the OC diagram differs from the ETP only in that it makes use of the climatic significance coefficients, which I have introduced. However, this formal difference is underlain by a fundamental dissimilarity between the ways these two curves have been interpreted in. The ETP, unlike the OC diagram, could not be employed as a paleoclimatic curve, because, according to the Milankovitch theory, the climate effect from eccentricity variations is negligibly small compared to the other two orbital elements. This is why the quantitative changes in the summer-time insolation under 65oN lat, as calculated by Milankovitch, and which he considered to be paleoclimatically significant, lack in insolation contribution linked directly to eccentricity variations, which is dominant in the OC diagram. Besides, it was shown above that insolation signals from the various orbital elements have distinctive structures and, hence, different climate forcing mechanisms, specific to each particular element and implemented via a variety of terrestrial feedbacks. Ultimately, it is these factors, and not summer insolation variations at 65o N lat, that determine their global climate significance. Hence, the OC diagram, which implies influence from the real factors just discussed, can be ranked as a paleoclimate curve, while the ETP cannot.
Comparison of the OC diagram and oxygen isotope curves shows a rather good fit, especially for OI stages 1-5, 7, 12-15, and 17 (Figures 4 and 5). All but one glaciation event (coincident with oxygen isotope Stage 6) over the last million years can be identified. Noteworthy is that the OC diagram maximum coinciding with the 19th oxygen isotope stage falls between 770 and 790 ka, in good agreement with the new age determination [Spell and McDougal, 1992] for the Matuyama-Brunhes magnetic reversal, which passes inside the 19th OI Stage [Bassinot et al., 1994; Bol'shakov, 1999; deMenocal et al., 1991; Schneider et al., 1992]. The crucial distinction of the OC diagram from the Milankovitch (and his followers') insolation diagrams, calculated for specific latitudes, is the virtually global character of the OC diagram [Bol'shakov, 2000a, 2000b, 2000c, 2001a, 2001b]. This is due partly to the fact that the climatic significance coefficient for precession (whose influence is thought to be in counterphase in the opposite hemispheres), adopted while constructing the OC diagram, is the lowest of all three orbital elements. It is thus reasonable to assume a delay in the climatic response to its corresponding orbital signal, caused by the huge inertia of the Earth climate system. It makes sense to determine this delay from the best dated global climate events, such as the Holocene optimum (5-6 ka ago) and the last glaciation maximum (21-22 ka ago). Comparing these dates with the corresponding OC diagram maximum and minimum shows that the climatic response was delayed some 5-6 ka [Bol'shakov, 2000a, 2001b]. This suggests that where the Matuyama-Brunhes reversal is found in deep water columns, these columns can be timed by simply correlating the most typical maxima and minima on the oxygen isotope curve from a given column to those on the OC diagram [Bol'shakov, 2001a, 2001b], thus avoiding the painstaking exercise of extracting the oxygen isotope climate cycles and tuning them to variations in the angle e and precession, as is done routinely [Bassinot et al., 1994; Hays et al., 1976; Imbrie et al., 1984; Shackleton et al., 1990]. The overall good match of the OC diagram with oxygen isotope curves is the first direct evidence ever obtained for the predominant influence of orbitally caused insolation variations on the rhythmicity and trend of global climate oscillations within the last million years.
Apparently, there are some discrepancies between the theoretically constructed OC diagram and oxygen isotope curves. The most conspicuous ones are (a) the mismatch between the 190-140 ka minimum on the OC diagram and OI Stage 6 glaciation and (b) the mismatch between the low value of the ca. 410 ka maximum on the OC diagram and the high peak on the OI curve identified as the 11th OI Stage. These discrepancies are most likely due to the aforesaid self-sustained oscillations in the system cryosphere-hydrosphere-lithosphere-atmosphere [Bol'shakov, 2000a, 2000b], considered by many researchers. Assumedly, the period of these oscillations may be ca. 100,000 years. These oscillations (forced by insolation variations and associated primarily with the waxing and waning of glaciers and the World Ocean temperature), in view of their enormous inertia, may have changed the amplitude of global climate oscillations and, to some extent, possibly stabilized this amplitude relative to the amplitude of the forcing insolation signal--in particular, for oxygen isotope Stages 6 and 11.
The likely existence of these forced self-sustained oscillations is also proposed by [Bol'shakov, 2000a, 2000b] to explain the transition, ca. 1 Ma ago, from the predominant 41-ka climate cyclicity to the 100-ka one [Imbrie et al., 1993; Ruddiman et al., 1986; Shackleton, 1995]. Apparently, in this case a mechanism could have come into play that resembles the parametric resonance mechanism, with the changing external conditions causing changes in the parameters of the system and its resonance frequencies. By a change in external conditions I mean the unidirectional cooling that set in as early as the Eocene, in the time interval from 2 to 1 Ma. This must have led to a change in the volume of high latitude glaciers and, consequently, to a change in their inertia. The likely mechanism of change in the rhythmicity of climate oscillations at 1 Ma may thus be presented [Bol'shakov, 2000b, 2001b] as follows. Prior to 1 Ma ago, ice volume was not large enough, and the planet's surface temperature not low enough, for ice to reach dimensions comparable to the sheet glaciation of the last million years. Hence, the change in the volume of glaciers clustered at high latitudes was governed by a relatively short-period forcing from the ecliptic tilt, in accordance with the empirically discovered, ca. 41 ka periodicity of this change. Long-period forcing from eccentricity variations and its related global oscillation in the planet's temperature proved to be too weak to cause the waxing of ice sheets. This is the reason why the corresponding 100-ka period variations were not pronounced in climate records of this time interval. Over time, with progressive global cooling, glaciers kept growing as well. Conceivably, at 1 Ma the planet's surface temperature and the mass of glaciers at high latitudes became critical with respect to the influence from insolation changes forced by eccentricity variations. In this case, the "eccentricity forced" temperature drop was sufficient to prevent glaciers that propagated from high latitudes from melting at lower latitudes. On the other hand, with increasing mass and area of glaciers, positive feedbacks due to albedo and the atmospheric content of greenhouse gases also increased, in turn to boost the advance of glaciation; naturally, the time constant of glacier waxing and waning increased, too. In my opinion, it was the interplay of these three factors that determined the new glaciation rhythmicity for the last million years. Therefore, the dynamics of development of global glaciations over the last million years has been mainly determined by a combined impact from eccentricity variations and the ecliptic tilt, amplified by the influence of positive feedbacks, modulating the general trend of global cooling. (Similar mechanisms for the "mid-Pleistocene transition," calling for a global increase in ice volume as a principal factor, were proposed by the other researchers as well [Berger, 1999; Clark et al., 1999; Imbrie et al., 1993]. However, these mechanisms do not invoke as decisively a governing role for the insolation signal forced immediately by eccentricity).
The above explanation suggests the following reasonable conclusion. Provided the global cooling, which began in the Eocene, goes on, then a further increase in ice volume will result not only in glacier expansion, but also in an increased period of glacier oscillations. Therefore, an eventual expansion of the modern glaciation should involve a climatic manifestation of a longer, 400-ka eccentricity cycle, which has not occurred for the past 2 Ma [Berger, 1999; Imbrie et al., 1993]. This corollary is further supported by the published data suggesting that the maximum phase of the Permo-Carboniferous glacial age was characterized by a 400-ka climate cyclicity [Heckel, 1986; Veevers and Powell, 1987]. It is common knowledge that the Permo-Carboniferous Gondwanan glaciation was especially extensive, reaching as far south as 30o S lat [Veevers and Powell, 1987]. Hence, these data can be taken to support the here proposed mechanism, which links insolation oscillations forced by variations in the axial tilt and eccentricity, changes in the volume of ice sheets, and the rhythmicity of ice waxing and waning.
Note that the proposed mechanism for global climate oscillations views glacials and interglacials as resulting almost solely from the influence of variations in eccentricity and tilt angle, with the principal feedback factor that amplifies the integrated orbital insolation signal being albedo variations due mainly to waxing and waning of ice sheets and snow cover at high and moderate latitudes. In other words, the global climate effect of precession has a subordinate role during these periods. This corollary is at odds with the fundamentals of the Milankovitch theory and the customary views of his followers, but it is supported by empirical data for at least the last two million years. According to these data [Berger, 1999; Imbrie et al., 1993; Ruddiman et al., 1986; Shackleton, 1995], the global climate effect of precessional variations is least pronounced in the OI signatures in deep water sediments. This is further supported by the fact that, from the general considerations presented above, the mechanism for global precessional influence on climate is the most debatable one.
The above suggests a central role for ice sheet volume in how the orbital periods of climate cycles manifest themselves. Hence, the lack of ice should bring about essentially different climate oscillation mechanisms. Assumedly, contrary to many researchers' opinion, any immediate manifestation of climate cycles forced by eccentricity variations and axial tilt during the thermal ages (or when global ice volumes are essentially smaller than in the Pleistocene) will be absent. This inference is additionally supported by the largely empirical data [Herbert and Fisher, 1986; Kent et al., 1995; Olsen, 1984, 1986]. Thus, the Mesozoic, Eocene, and Miocene have mainly 23-ka (precessional) climate oscillations, modulated by eccentricity variations. No independent manifestations of the other orbital cycles have been recorded.
The above interpretation of paleoclimate data acquired to date suggests a new concept for the orbital theory of paleoclimate. This concept contributes essentially to and renders more concrete the rather general pioneering hypothesis linking the variations in orbital elements to global climate oscillations; it also differs considerably from the concepts of the orbital theory of paleoclimate proposed by the other writers--e.g., [Croll, 1875] and Milankovitch [1939]. This concept is formulated as follows [Bol'shakov, 2001b]:
(1) The extent and character of the climatic effect of variations in orbital elements depend on the global paleoclimate state of the Earth (ranging from a thermal age to a glacial age), which is determined, most likely, by both terrestrial and extraterrestrial circumstances alike.
(2) Establishing the climatic significance of the variations in each of the three orbital elements requires taking continuously into account how insolation varies over time and through space, while concomitantly accounting for and further refining mechanisms for the Earth climate feedbacks, through which orbital signals are transformed to global climate changes.
Let us emphasize the main distinctions of the new concept from the numerous other existing interpretations of empirical data.
(a) The new concept maintains that climatic influence of orbitally caused insolation variations is governed, firstly, by the modes in which insolation signal is transformed to global climate changes (terrestrial feedback mechanisms), whose very existence depends on the global climatic state of the Earth, and secondly, by time- and space-continuous (and not discrete) insolation variations.
(b) Noteworthy are the simplicity and self-evidence of the basic tenets used in constructing the OC diagram, which requires no quantification of insolation changes, while drawing solely on the general mechanisms for climatic influence from individual orbital elements. However, the choice of specific climatic significance coefficients attributed to variations in each particular orbital element is performed with due account for empirical data. Such account, though, provides the basis for all the theoretical paleoclimate models. Moreover, it is for the first time ever that a logical and realistic substantiation has been provided for the different degrees of climatic significance of the variations in individual orbital elements (which depend on (i) the structure of their related insolation signals and regional peculiarities of their influence and (ii) the general global climatic situation during the time span under study).
(c) The tenets developed in the framework of the new concept permit a much simpler explanation for the synchroneity of global climate oscillations than, e.g., in [Broecker and Denton, 1989].
(d) The new concept of the orbital theory of paleoclimate enables one, for the first time ever and on a solid conceptual basis, to propose an internally consistent overview of climate oscillations (ranging in period from several tens to several hundreds of thousand years) not only for the Quaternary, but also for the older geological periods of the Phanerozoic.
At a qualitative level, the model for global climate oscillations over the last million years, in view of the good agreement of the OC diagram with oxygen isotope curves and the general mechanism adopted for orbitally forced climate variations, can be presented as follows. Orbital changes force insolation variations, which in turn induce initial temperature changes (mainly at high latitudes), resulting through positive feedback (due to variations in the volume and area of ice and snow at these latitudes) in still more considerable temperature oscillations involving larger areas. These oscillations in turn influence more strongly the World Ocean temperature and the atmospheric concentrations of greenhouse gases, the combined action of the totality of factors then determining the resultant global oscillations in ice volume and temperature (climate oscillations). It thus follows that insolation variations and global ice volume changes, rather than variations in the atmospheric concentrations of greenhouse gases (in particular, CO 2 ), have been the underlying cause of global climate changes in the Quaternary. Note the lack of consensus on this issue [Berger et al., 1998; Imbrie et al., 1993; Petit et al., 1999; Shackleton, 2000], which might be due to the interdependency of the above climate factors, on which we have focused as well.
The technique used in constructing the OC diagram and its correlation to oxygen isotope records [Bol'shakov, 2000a, 2001b] permit ranking the OC diagram as an independent standard, obtained on the basis of theoretical considerations and portraying global paleoclimate changes in the Pleistocene. Not only does the availability of such an independent standard make for a more unbiased correlation of paleoclimate events that have certain singular features and are recorded in deposits of various geneses (primarily, continental), but it also helps to extract the most adequate paleoclimate signatures from deep water sediments. The point is that oxygen isotope records from several deep sea columns, recording global ice volume changes, usually differ somewhat from each other. Nothing can warrant that averaging these records for several columns (a procedure resembling SPECMAP oxygen isotope scale construction [Imbrie et al., 1984]) will provide the most adequate record of these changes. Among the advantages of the proposed technique is the possibility of adjusting the relationships among the climatic significance coefficients for the orbital elements so as to achieve the best fit between the OC diagram and paleoclimatic data. In this manner, one can emphasize the singular way in which the variations in each particular orbital element force climate changes, as documented in various paleoclimatic records both through time and in space. Recall that initially, the values of the climatic significance coefficients used in constructing the OC diagram were determined from the best fit between the OC diagram and the most trustworthy oxygen isotope records from deep water sediments. Conversely, at the present by adjusting the values of the climatic significance coefficients, one may achieve the best fit of the OC diagram to various paleoclimate records. This can be used for visualizing the degree of influence from the variations of individual orbital elements in various regions and for different geological intervals. This technique resembles the spectral-time analysis, as implemented by [Imbrie et al., 1993], although it has some distinctive features due to a different theoretical basis used to interpret empirical data and to the graphical correlation of the theoretically constructed OC diagram and paleoclimate curves.
Apparently, correlating paleoclimate curves to the OC diagram based only on their shape and the outward similarity of these curves may prove unreliable. Required is at least one time benchmark on the oxygen isotope record within the 1 Ma timespan. Such a benchmark is usually provided by the Matuyama-Bruhnes reversal, occurring almost in the middle of the 19th oxygen isotope stage, and its corresponding OC diagram maximum at ca. 780 ka. Because it is known that above this maximum the record must show eight glacial-interglacial cycles, one can use comparisons with the OC diagram to draw conclusions as for how complete the geological record is and concerning the peculiarities of the paleoclimate signature of the oxygen isotope curve under study. The same applies to terrestrial sections, the precision of correlations increasing with the number of levels dated. Evidently, the validity of correlation will also depend on how adequately the paleoclimate curves portray the events that match in rank with glacials and interglacials, which are identified with the greatest confidence on the OC diagram. Not inconceivably, comparing the OC diagram with independently acquired paleoclimate data from terrestrial and deep water deposits would also help to resolve some of the less important (compared to those mentioned above) misfits between the OC diagram and oxygen isotope records (Figures 4 and 5). It is a question whether these misfits portray some subtleties of climate changes related to terrestrial conditions and not recorded in the OC diagram, or whether these are defects of the oxygen isotope record. The discrepancies and defects of paleoclimate records might also be an artifact of, e.g., an intention of extracting orbital cycles from these records no matter what.

|
| Figure 6 |

|
| Figure 7 |
Winograd et al. [1992], while analyzing the d 18O signature they obtained from calcite, found the duration of the four last glacial cycles to have increased from 80 ka to 130 ka. This has enabled the conclusions that "...major climate changes were aperiodic" and that "...orbitally controlled variations in solar insolation were not a major factor in triggering deglaciations" [Winograd et al., 1992, p. 255]. However, my own correlation of the OC diagram to the d 18O calcite curve shows convincingly that it was the orbitally forced insolation variations that determined the rhythmicity and trend (warming vs. cooling) of climate oscillations (Figure 7). The varying duration of the glacial-interglacial cycles is governed by insolation variations and requires no additional mechanisms to explain these changes, such as are proposed in [Elkibby and Rial, 2001; Rial, 1999].
Analyzing the data shown on Figures 4, 5, 6, and 7 suggests that the orbital climate diagram can be employed as a general, and, hence, sufficiently independent standard for global paleoclimate oscillations in the Pleistocene. The above comparisons of the OC diagram with paleoclimate records from deep water deposits, the ice core from Antarctica, and the calcite layer from North America have shown a generally good agreement. This implies that the principal paleoclimate events of the Pleistocene correlate tightly between various regions of the planet and that the factors governing paleoclimate cycles had a global character. Clearly, one of such factors is the orbitally caused insolation variations. The above comparisons of paleoclimate signatures with the OC diagram also demonstrate the principal discrepancies that are similar in all three case studies, and that are due to the signature of paleoclimate events corresponding to the 6th and 11th oxygen isotope stages in deep water sediments. This might imply factors other than orbital variations (but also of a global character) to have influenced Earth paleoclimate in the Pleistocene. As mentioned above, I believe that one of the most viable explanations for these misfits is that in the Pleistocene there acted a mechanism for forced self-sustained oscillations in the system atmosphere-hydrosphere-cryosphere-lithosphere, as discussed by many researchers (e.g., [Imbrie et al., 1993]). The interplay of the above four critical nearsurface shells of the planet is likely to ensure their global impact on Earth climates. However, these mismatches (both major and minor) between the OC diagram and paleoclimate records require a further study (in particular, by comparing the OC diagram with as many independently acquired and properly substantiated paleoclimatic data as possible).
|
| Figure 8 |
This work addresses the main phases of and prerequisites for developing the orbital theory of paleoclimate. It has to be stated that the creation of this theory is far from being complete, despite the efforts of many generations of researchers over the past century and a half. The Milankovitch theory is merely a version of the orbital theory of paleoclimate, each existing version having its own concept, its advantages and drawbacks, and, as it turned out, considerable inconsistencies with empirical data. It has also been shown that insolation curves calculated for individual latitudes and half-years, let alone months or days, bear no paleoclimatic implications and are of no use to paleoclimate modeling. The calculations of orbitally caused insolation changes, as performed by Milankovitch, outstripped their time. Making a full use of these calculations requires a steadfast identification and validation of the specific mechanisms through which orbitally forced insolation variations are transformed to global climate changes.
In keeping with the available paleoclimate data for the Pleistocene and for the entire Phanerozoic, proposed is a simple scheme (concept) of how variations in orbital elements cause global climate changes. This scheme draws on accounting for time- and space-continuous (and not discrete) insolation variations, caused by variations in individual orbital elements and on the rather self-evident general mechanisms of their climatic influence. A pivotal factor to developing the new concept was the construction of the OC diagram, which accommodates well the empirical data.
Comparing the OC diagram to empirical data, performed above, demonstrates the possibility of solving the most challenging issues of the orbital theory based on the orbital theory of paleoclimate alone, without invoking auxiliary speculations or mechanisms that require additional validation. What is meant here is issues such as the prevalence of the 100-ka and lack of the 400-ka climatic periods, unequal durations of glacial cycles, glacial events coinciding with eccentricity minima over the last million years, the Middle Pleistocene transition, and certain issues of how the climate changes linked to orbital periodicities manifest themselves during Phanerozoic thermal and glacial ages.
For the first time, demonstrated has been the importance of accounting for how insolation signals (linked to variations in a set of orbital elements) are distributed over time and space (across the Earth surface) and, accordingly, for the singularity of feedback mechanisms operating in the Earth climate system and also changing in time and space. Considering the differences in the temporal and spatial structures of insolation signals linked to individual orbital elements, it appears unreasonable to differentiate the mechanisms for climatic amplification of these signals into linear and non-linear. It is more sensible to speak of individual amplification mechanisms, while bearing in mind that in different geological times these mechanisms can manifest themselves in different ways or in no way at all.
Our considerations indicate quite definitely and clearly that the total insolation change resulting from variations in all three orbital elements determines the rhythmicity and trend of climate changes, while the cycles themselves (i.e., the shape of the empirically obtained paleoclimate curves) are mainly determined by the mechanisms of influence from various feedbacks that change through time and space.
As noted above, constructing a rigorously quantified model would require taking into account time- and space-continuous insolation changes (i.e., such as could be calculated following the Milankovitch method, but additionally integrated along the year and along all the latitudes), while also accounting for terrestrial feedbacks, which can be of either a global or regional character. It is only by using these really globally operating factors that one may quantify the degree of global climate forcing from variations in orbital elements and the various feedbacks. In particular, this applies to variations in albedo of the Earth surface and in the atmospheric concentration of greenhouse gases, which is currently a burning issue to the forecasts of global climate change. Forecasting global climate change based on paleoclimate models where the input signal is a monthly, let alone a daily mean insolation incident on the upper boundary of the atmosphere at a single arbitrarily chosen latitude (usually 65o N), would hardly make sense. This is because creating a paleoclimate model involves establishing the mechanism for transforming the input (insolation) signal to the output signal, which is represented by paleoclimate data (e.g., curves showing variations in the content of the heavy oxygen isotope along bottom sediment columns). However, the input signal in this case does not fully reflect the changes in the solar radiation incident on the Earth and really influencing the Earth climate. Hence, a mechanism for transforming an inadequate input insolation signal to real climate changes would itself be inadequate.
The OC diagram can be used to forecast natural global change. By extending it to the future, it can be inferred that within the 60 ka to come the Earth will experience two glacial phases with their peaks at 20,000 yrs and 60,000 yrs from the present. How this natural climate trend will be affected by anthropogenic activity and, primarily, by the growing atmospheric concentration of greenhouse gases, can only be established on the basis of a precise enough estimate of the past geological effects of variations in the contents of atmospheric greenhouse gases. To date, no in-depth study has been performed to quantify the atmospheric CO 2 content required for warming to overrule the natural cooling trend.
An Atlas of Temporal Variations in Natural, Anthropogenic, and Social Processes, Volume 2, Cyclic Dynamics in Nature and Society, Nauch. Mir, Moscow, 1998.
Barron, E., M. Arthur, E. Kauffman, Cretaceous rhythmic bedding sequence: a plausible link between orbital variations and climate, Earth Planet Sci. Lett., 72, 327-340, 1985.
Bassinot, F. C., L. D. Labeurie, E. Vincent, et al., The astronomical theory of climate and the age of the Brunhes-Matuyama magnetic reversal, Earth Planet. Sci. Lett., 126, 91-108, 1994.
Berger, A., Theorie astronomique des paleoclimate, une nouvelle approche, Bull. Soc. Belge Geologie, 87, 9-25, 1978.
Berger, A., Milankovitch theory and climate, Revs. Geophysics, 26, 624-657, 1988.
Berger, A., and M. F. Loutre, Insolation values for the climate of the last 10 million years, Quat. Sci. Rev., 10, 297-317, 1991.
Berger, A., M. Loutre, and H. Gallee, Sensitivity of the LLN climate model to the astronomical and CO 2 forcings over the last 200 ky, Climate Dynamics, 14, 615-629, 1998.
Berger, W. H., The 100-kyr ice-age cycle: internal oscillation or inclinational forcing?, Int. Journ. Earth Sciences, 88, 305-316, 1999.
Bol'shakov, V. A., M. Milankovitch's paleoclimate theory: Certain problems and their possible solutions (in Russian), Vestn. Mosk. Gos. Univ., Geogr., 5, (68), 1998, deposited at VINITI, 2299, 18 pp. 20.07.1998.
Bol'shakov, V. A., On the depth of paleomagnetic record acquisition by deep-sea sediments with reference to the climatic-stratigraphic position of the Matuyama-Brunhes reversal, Izvestiya, Physics of the Solid Earth, 35, 522-525, 1999.
Bol'shakov, V. A., The theory of M. Milankovitch: A new concept, Izv. Ross. Akad. Nauk, Geogr., 1, 20-30, 2000a.
Bol'shakov, V. A., A new concept of the astronomical theory of paleoclimate, in The Issues of the Paleogeography and Stratigraphy of the Pleistocene, pp. 35-69, Moscow State Univ., Moscow, 2000b.
Bol'shakov, V. A., A new method of plotting paleoclimatic variations in the Pleistocene, Doklady, Earth Sciences. 375, 128-1282, 2000c.
Bol'shakov, V. A., The orbital climatic diagram as a basis for comparing Pleistocene paleoclimatic records, Doklady, Earth Sciences, 379, 675-678, 2001a.
Bol'shakov, V. A., A new concept of the astronomical theory of paleoclimate: Two steps backwards, one step forwards, Izvestiya, Physics of the Solid Earth, 37, 960-916, 2001b.
Bol'shakov, V. A., The new method of the time study of a deep-sea cores oxygen-isotope records, Doklady, Earth Sciences, 382, 112-114, 2003.
Bol'shakov, V. A., and P. V. Bol'shakov, A New Concept of the Astronomical Theory of Paleoclimate, Stratigr. Geol. Correlation, 7, 521-530. 1999.
Broecker, W. S., and G. H. Denton, The role of ocean-atmosphere reorganizations in glacial cycles, Geochim. Cosmochim. Acta., 53, 2465-2501, 1989.
Budyko, M. I., Global ecology, 327 p., Mysl', Moscow, 1977.
Chistyakov, V. F., Solar cycles and climate oscillations, 156 p., Dal'nauka, Vladivostok, 1997.
Clark, P., R. Alley, and D. Pollard, Northen Hemisphere ice-sheet influences on Global Climate Change, Science, 286, 1104-1111, 1999.
Clemens, S., and W. Prell, Late Quaternary forcing of Indian Ocean summer-monsoon winds: a comparison of Fourier model and General Circulation Model results, J. of Geophys. Res., 96, (D12), 22,683-22,700, 1991.
Cowie, C., The Earth orbit and glacial epochs (in Russian), V Mire Nauki, 4, 26-35, 1984.
Croll, J., Climate and time in their geological relations: a theory of secular changes of the Earth's climate, 577 pp., Edward Stanford, London, 1875.
deMenocal, P. B., W. F. Ruddiman, and D. V. Kent, Depth of post-depositional remanence acquisition in deep-sea sediments: a case study of the Brunhes-Matuyama reversal and oxygen isotopic Stage 19.1, Earth Planet. Sci. Lett., 99, 1-13, 1991.
Elkibbi, M., and J. Rial, An outsider's review of the astronomical theory of the climate: is the eccentricity-driven insolation the main driver of the ice ages?, Earth-Science Reviews, 56, 161-177, 2001.
Hays, J. D., J. Imbrie, and N. Shackleton, Variation in the Earth's orbit: Pacemaker of the ice ages, Science, 194, 1121-1132, 1976.
Heckel, P. H., Sea-level curve for Pennsylvanian eustatic marine transgressive-regressive depositional cycles along midcontinent outcrop belt, North America, Geology, 14, 330-334, 1986.
Herbert, T., and A. Fisher, Milankovitch climatic origin of mid-Cretaceous black shale rhythms in central Italy, Nature, 321, 739-743, 1986.
Imbrie, J., Astronomical theory of the Pleistocene Ice Ages: a brief historical review, Icarus, 50, 408-422, 1982.
Imbrie, J., and J. Z. Imbrie, Modeling the climatic response to orbital variations, Science, 207, 943-953, 1980.
Imbrie, J., and K. P. Imbrie, Misteries of ice ages, 264 p., Progress, Moscow, 1988.
Imbrie, J., and K. P. Imbrie, Ice Ages, Solving the Mystery, Enslow, Hillside, N. J., 1979.
Imbrie, J., J. Hays, D. Martinson, et al., The orbital theory of Pleistocene climate: support from a revised chronology of the marine d 18O record, in Milankovitch and Climate, NATO ASI Ser., C. 126., edited by A. I. Berger et al., pp. 269-305, Reidel, Dordrecht, 1984.
Imbrie, J., A. Berger, A. Boyle, et al., On the structure and origin of major glaciation cycles, 2. The 100,000-year cycle, Paleoceanography, 8, 699-735, 1993.
Johnson, R. J., Brunhes-Matuyama magnetic reversal at 790,000 yr., B.P. by marine-astronomical correlations, Quatern. Res., 17, 135-147, 1982.
Kent, D., P. Olsen, and W. Witte, Late Triassic-earliest Jurassic geomagnetic polarity sequence and paleolatitudes from drill cores in the Newark rift basin, eastern North America, J. Geophys. Res., 100, 14,965-14,998, 1995.
Kominz, M., and N. Pisias, Pleistocene climate: deterministic or stochastic?, Science, 204, 171-173, 1979.
Laskar, J., F. Jotel, and F. Boudin, Orbital, precessional, and insolation quantities for the Earth from - 20 Myr to +10 Myr, Astron. Astrophys., 270, 522-533, 1993.
Milankovitch, M., Mathematische Klimalehre und astronomische Theorie der Klimaschwankungen, Handbuch der Klimatologie, 1, A, 176 pp., Gebruder Borntraeger, Berlin, 1930, GONTI, Moscow, 1939.
Oerlemans, J., Model experiments on the 100,000-yr glacial cycle, Nature, 287, 430-432, 1980.
Olsen, P. E., Periodicity of lake-level cycles in the Late Triassic Lockatong formation of the Newark Basin, in Milankovitch and Climate, NATO ASI Ser. C. 126, edited by A. I. Berger et al., Reidel, pp. 133-146, Dordrecht, 1984.
Olsen, P. E., A 40-Million-year lake record of Early Mesozoic orbital climatic forcing, Science, 234, 842-848, 1986.
Petit, J., J. Jouzel, D. Raynaud, et al., Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica, Nature, 399, 429-436, 1999.
Pisias N., and D. Rea, Late Pleistocene paleoclimatology of the central equatorial Pacific: sea surface responce to the southeast trade winds, Paleoceanography, 3, 21-27, 1988.
Prell, W., and J. Kutzbach, Monsoon variability over the past 150,000 years, J. Geophys. Res., 92, 8411-8425, 1987.
Prokopenko, A., E. Karabanov, D. Williams, et al., Biogenic silica record of the lake Baikal response to climatic forcing during the Brunhes, Quatern. Res., 55, 123-132, 2001.
Rial, J. A., Pacemaking the Ice ages by frequency modulation of Earth's orbital eccentric-ity, Science, 285, 564-568, 1999.
Ridgwell, A., A. Watson, and M. Raymo, Is the spectral signature of the 100 kyr glacial cycle consistent with a Milankovitch origin?, Paleoceanography, 14, (4), 437-440, 1999.
Rossignol-Strick, M., African monsoons, an immediate climate response to orbital insolation, Nature, 304, 46-49, 1983.
Ruddiman, W. F., M. Raymo, and A. McIntyre, Matuyama 41,000-year cycles: North Atlantic Ocean and northern hemisphere ice sheets, Earth Planet. Sci. Lett., 80, 117-129, 1986.
Schneider, D. A., D. V. Kent, and G. A. Mello, A detailed chronology of the Australasian impact event, the Brunhes-Matuyama geomagnetic Polarity reversal, and global climate change, Earth Planet. Sci. Lett., 111, 395-405, 1992.
Schwarzbach, M., Das klima der vorzeit Eine Einfuhrung in die Palaoklimatologie, Stutgart, 1950, IL, Moscow, 1955.
Sergin, V., and S. Sergin, How the Earth glaciations originated (in Russian), Priroda, 9, 10-17, 1969.
Shackleton, N., New data on the evolution of Pliocene climatic stability, in Paleoclimate and Evolution with Emphasis on Human Origins, edited by E. S. Vrba et al., pp. 242-248, Yale University Press, 1995.
Shackleton, N., The 100,000-year ice-age cycle identified and found to lag temperature, carbon dioxide, and orbital eccentricity, Science, 289, 1897-1902, 2000.
Shackleton, N. J., A. Berger, and W. Peltier, An alternative astronomical calibration of the lower Pleistocene time scale based on ODP Site 677, Trans. R. Soc. Edinb., 81, 251-261, 1990.
Shaw, D., and W. Donn, Milankovitch radiation variations: a quantitative evaluation, Science, 162, 1270-1272, 1968.
Spell, T. L., and I. McDougall, Revisions to the age of the Brunhes-Matuyama boundary and the Pleistocene geomagnetic polarity timescale, Geophys. Res. Letters, 19, 1181-1184, 1992.
Veevers, J. J., and C. M. A. Powell, Late Paleozoic glacial episodes in Gondwanaland reflected in transgressive-regressive depositional sequence in Euramerica, Geol. Soc. Amer. Bull., 94, 475-487, 1987.
Weertman, J., Milankovitch solar radiation variations and ice age ice sheet sizes, Nature, 261, 17-20, 1976.
Wigley, T. M. L., Spectral analysis and the astronomical theory of climatic change, Nature, 264, 629-631, 1976.
Winograd, I. J., T. Coplen, J. Landwehr, et al., Continuous 500,000-year climate record from vein calcite in Devils Hole, Nevada, Science, 258, 255-260, 1992.
Wundt, W., Die Wirkung der Erbahnelemente bei der Entstehung der Eiszeiten, Geol. Rundschau, 34, 7-8, 1944.