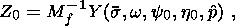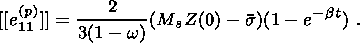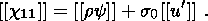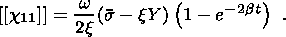Russian Journal of Earth Sciences
Vol. 4, No. 2, April 2002
Thermomechanics of phase transitions of the first order in solids
V. I. Kondaurov
Moscow Institute of Physics and Technology, Moscow, Russia
Contents
Abstract
Methods of nonequilibrium thermodynamics and continuum mechanics
are used for
studying phase transitions of the first order in deformable solids with elastic
and viscoelastic rheology. A phase transition of the first order is treated as
the transition from one branch of the response functional to another as soon as
state parameters reach certain threshold values determined by thermodynamic
phase potentials and boundary conditions of the problem. Notions of kinematic
and rheological characteristics of a phase transition associated with the change
of the symmetry group due to the structural transformation and with the
difference between thermodynamic potentials in undistorted phase configurations
are introduced. In a quasi-thermostatic approximation, when inertia forces and
temperature gradients are small, a close system of equations on the interface
between deformable solid phases is formulated using laws of conservation. The
system of the latter includes, in addition to the traditional balance equations
of mass, momentum and energy, the divergence equation ensuring the compatibility
of finite strains and velocities. As distinct from the classical case of the
liquid (gas) phase equilibrium, the phase transition in solids is supposed to be
irreversible due to the presence of singular sources of entropy of the delta
function type whose carrier concentrates on the interface between the phases.
The relations on the interface including the continuity conditions of the
displacement vector, temperature, mass flux and the stress vector, as well as a
certain restraint imposed on the jump of the normal component of the chemical
potential tensor, are discussed. The latter restraint makes the resulting
relations basically distinct from the classical conditions of the phase
equilibrium.
A generalized Clapeyron-Clausius equation governing the differential dependence
of the phase transition temperature on the initial phase deformation is
formulated. The paper presents a new relation of the phase transformation
theory, namely, the equation describing the differential dependence of the phase
transition temperature on the interface orientation relative to the anisotropy
axes and the principal axes of the initial phase strain tensor. Based on the
relations derived in this study, the phase transformation temperature of an
initially isotropic material is shown to assume extreme values if the normal to
the interface coincides with the direction of a principal axis of the initial
phase strain tensor. The phase transition of the first order in a linear
thermoelastic material with small strain values and small deviations of the
temperature from its initial value is discussed in detail. A class of materials
is distinguished in which an increase in the initial phase strain necessarily
changes the character of the phase transformation (a normal phase transition
becomes an anomalous one and vice versa). The equilibrium of a compressed
viscoelastic layer admitting melting and the effect of stress relaxation in the
solid phase on the fluid boundary motion are examined.
1. Introduction
As is experimentally shown, nearly all materials experience phase transitions
under sufficiently intense thermal and mechanical loads. Two cases can be
distinguished depending on properties of the phase material. In the first case,
new phase nuclei unboundedly grow and coalesce, finally forming large regions
each consisting of only one phase. The contact surface of such a region, below
referred to as an interface, is a surface at which some thermodynamic parameters
and their first derivatives are discontinuous. One of the main problems of the
phenomenological theory of such transitions is to specify the relations between
various quantities at the interface. In the second case, energy factors and
kinetic properties restrict the growth of new phase nuclei by medium-scale sizes
that are small compared to the characteristic size of a body. The accumulation
of nuclei that do not coalesce gives rise to a mixture of two phases and a
composite structure consisting of an initial phase matrix "reinforced" by
inclusions of the new phase disseminated throughout its volume. In this case, in
addition to the problem of determining the effective properties of this type of
materials, which is traditional in the mechanics of composites, one often
encounters the problem the phenomenological description of the concentration,
spatial distribution and shape of the new phase inclusions as a function of
varying stress (strain) and thermal state. In this study I restrict myself to
the first case (below referred to as the phase transition of the first order in
accordance with the generally accepted terminology).
The majority of natural processes are associated with or even due to phase
transformations of materials
[Turcott and Schubert, 1982],
and many of these processes are critically dependent on not only the temperature
and
pressure but also tangential stresses. Examples are tectonic processes, metamorphism
phenomena, stratification in the crust and recrystallization of geomaterials.
The formation of deep-seated sources of earthquakes is associated with the
relaxation of deviatoric stresses in the vicinity of a moving front of phase
transformations. The orientation and shape of magma chambers essentially depend
on the presence of shear stresses and thermoelastic properties of the
surrounding rocks. The list of geophysical examples alone can be continued.
However, even the aforesaid clearly indicates the relevance of the correct
description of the problem of solid phase transformations.
Mechanics and thermodynamics of phase transformations of deformable solids have
been developed over more than a century
[Gibbs, 1906].
The theory of liquid and gas phase equilibrium reducing to the equality of pressures,
temperatures and chemical potentials has become a constituent of the classical
thermodynamics and statistical mechanics
[Landau and Lifshits, 1964]
and a working tool in solving many scientific, engineering and technological problems
[Christian, 1978;
Khachaturyan, 1974;
Roitburd, 1974].
On the other hand, the Gibbs approach to the
description of the phase equilibrium conditions brought about many studies
intended to extend this approach to deformable solids in a nonhydrostatic stress
state and to the construction of the scalar chemical potential in media
characterized by more than two scalar parameters of state. Such studies are
reviewed, for example, in
[Grinfeld, 1990;
Ostapenko, 1977],
where these problems are also discussed in detail. Investigations in this direction
continue presently as well
[Knyazeva, 1999].
The first question arising in phenomenological simulation of phase
transformations is the following: How can the first-order phase transition be
defined in terms of the continuum mechanics? In the existing literature, this
question is either ignored or the phase transition is treated as a change in the
aggregate state of a solid, which is simply a paraphrase reducing to the
replacement of one term by another, equally indefinite term. Some authors invoke
to the structure of the medium and to the size and other characteristics of the
solid lattice, i.e. to the notions beyond the system of concepts of continuum
mechanics and thermodynamics. Phases are, at best, defined as states of the
matter coexisting as macroscopic regions that are at equilibrium with each other
and are separated by surfaces at which some thermodynamic potentials are
discontinuous
[Landau and Lifshits, 1964].
Setting aside insignificant, in my
opinion, limitations inherent in a purely static case, this definition
implicitly refers to the main problem related to the loss of uniqueness of the
response of the medium to a given thermodynamic state. In what follows,
remaining within the framework of thermodynamics of irreversible processes,
phase transitions of the first order in a continuum will be understood as
processes associated with the transition of a material element from one branch
of the response functional or function to another. The main problem in the
theory of first-order phase transitions is the thermodynamic conditions
consistent with such a transition; the latter can be either slow or rapid
(dynamic) transition. As distinct from the traditional approach based on
variational principles, this work describes the first-order phase transitions
in deformable solids within the framework of the theory of strong
discontinuities in the solution of partial differential equations describing the
behavior of the continuum studied. The necessary condition for constructing a
closed system of equations involving strong discontinuities is the possibility
of representing the equations as a system of conservation laws, which means that
these equations can be written in a divergent form. Hence, the first-order phase
transition in materials of the Prandtl-Reuss elastic-plastic type of the medium
[Sedov, 1970],
equations of which are basically irreducible to a divergent form
in the case of a multidimensional strain state, cannot be described in terms of
the conventional approach and require the application of the general theory of
strong discontinuities
[Sadovskii, 1997].
From the standpoint of the approach adopted in this study, the phase transition
can be realized not only in materials described by a general equation of state
of the Van der Waals type whose nonconvexity ensures the nonuniqueness of the
material response to a given state. As is shown below, phase transformations can
be experienced by materials the responses of which are described by different,
completely independent equations of state of each of the phases present.
Moreover, each of these constitutive equations can satisfy the convexity
condition and other classical restraints imposed on thermodynamic potentials.
Note also that, in constructing the so-called wide-range equations of state with
high densities of energy, the plane of state variables is often subdivided into
fields of different states of phases
[Bushman et al., 1992;
Melosh, 1989].
Such a subdivision is an approximate approach because the localization of various
phase fields ignores the solid-state properties of the material, the loading
rate dependence of the phase equilibrium conditions and the possible overlapping
of the areas of phase existence. Such an approximation cannot be substantiated
by a local thermodynamic equilibrium of the material element. A characteristic
example is the distinction of the Hugoniot adiabat describing the behavior of a
material under a shock load from the isotherm corresponding to a slowly varying
mechanical and thermal load.
The quasi-thermostatic approximation is often applied to the modeling of first-order
phase transitions caused by slowly varying mechanical and thermal loads.
This approximation implies that the state of a material element is supposed to
be close to a thermomechanical equilibrium characterized by a temperature
gradient
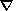 q
q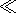 q0/l0 and
an Euler number
r0v20/s0
q0/l0 and
an Euler number
r0v20/s0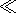 1,
where
q0, l0, r0,
v0 and
s0 are the characteristic temperature,
linear size of the body, density, velocity and pressure, respectively. It is additionally
assumed that the velocity of the interface is small compared to the velocity of sound,
and no
singular sources of mass, momentum, energy and entropy are present on the
interface.
1,
where
q0, l0, r0,
v0 and
s0 are the characteristic temperature,
linear size of the body, density, velocity and pressure, respectively. It is additionally
assumed that the velocity of the interface is small compared to the velocity of sound,
and no
singular sources of mass, momentum, energy and entropy are present on the
interface.
The assumption of the smallness of temperature gradients means that the model
used precludes temperature discontinuities, because otherwise the temperature
gradient between two points on opposite sides of the discontinuity surface will
be infinitely large. The quasi-static approach implies that the inertia forces
and kinetic energy are neglected in the equations of motion and energy balance,
respectively. The absence of a singular source of entropy means that the phase
transition in such a material is a reversible process for which the Clausius-Duhem
inequality becomes an equality. Hence, dissipation vanishes not only in
smooth flow areas but also as a particle crosses the interface. The phase
transition reversibility assumption is less evident and is often used
implicitly, particularly if phase transitions are described in terms of
variational principles of the continuum mechanics
[Grinfeld, 1990].
2. Basic Relations of a Thermoelastic Medium
Before deriving relations on a strong discontinuity surface separating different
solid phases, I remind the reader of the basic definitions and formulas of the
theory thermoelastic solids. The state of a material point
X of a thermoelastic
medium at a time moment
t is specified by the set of quantities
where F is the gradient of the mapping
k c(t)
of the reference configuration
of the body
k into the current configuration
c(t). The nonsymmetric
second-rank tensor F connects the radius-vectors differentials of two
neighboring material points:
c(t)
of the reference configuration
of the body
k into the current configuration
c(t). The nonsymmetric
second-rank tensor F connects the radius-vectors differentials of two
neighboring material points:
where
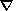 0 is the gradient in the Lagrangian
(substantial) variables
X
0 is the gradient in the Lagrangian
(substantial) variables
X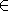 k.
The following polar decomposition holds for the nonsingular tensor F:
k.
The following polar decomposition holds for the nonsingular tensor F:
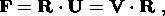 | (2.1) |
where R is an orthogonal tensor characterizing a rigid rotation of the material
element as a whole, and U and V are symmetrical, positively definite
tensors
describing the deformation of this element.
The current response of the material point X of a thermoelastic material
at
the time moment
t is characterized by the set of quantities
where T is the symmetrical Cauchy tensor of stresses, q is the heat
flux
vector,
h is the entropy density and
y is the free energy density
connected with the internal energy density through the relation
y = u - qh. The
scalar
q is the absolute temperature,
g
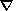 q is the temperature gradient
and
q is the temperature gradient
and
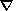 is the gradient in Eulerian (spatial) variables
x
is the gradient in Eulerian (spatial) variables
x 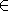 c (t).
In a
thermoelastic material, the current response
S ( X, t) is supposedly a function
of the
current state
l( X, t), i.e.
c (t).
In a
thermoelastic material, the current response
S ( X, t) is supposedly a function
of the
current state
l( X, t), i.e.
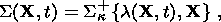 | (2.2) |
where
S+k { T+, y+,
h+, q+} is a set
of functions that effect the mapping
l( X, t)
{ T+, y+,
h+, q+} is a set
of functions that effect the mapping
l( X, t) S( X, t) and specify mechanical and thermal
properties of the
material. Below, these functions are referred to as constitutive functions or
relations. The index
k indicates the dependence of the constitutive
mappings on
the choice of the reference configuration of the body.
S( X, t) and specify mechanical and thermal
properties of the
material. Below, these functions are referred to as constitutive functions or
relations. The index
k indicates the dependence of the constitutive
mappings on
the choice of the reference configuration of the body.
The thermoelastic materials under consideration include both liquids and solids.
In the particular case
q = const, corresponding to the isothermal approximation,
the constitutive relations are transformed into the model of a hyperelastic
material; if undeformable heat-conductive solids are considered ( F is an
orthogonal tensor in any motion), the thermoelastic model reduces to the
traditional theory of heat conduction.
A necessary and sufficient condition for the validity of the second law of
thermodynamics (Clausius-Duhem inequality)
in any smooth process of state variation is given by the following restraints on
the constitutive relations of the thermoelastic medium
[Truesdell, 1972]:
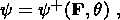 | (2.3) |
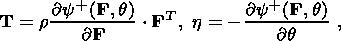 | (2.4) |
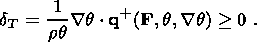 | (2.5) |
Relations (2.3) and (2.4) mean that, first, the free energy density of the
thermoelastic medium is independent of the temperature gradient; this is not an
assumption but a statement proven on the basis of general assumptions of the
continuum mechanics. Second, the stress tensor and entropy density of the
thermoelastic material are fully determined by the partial derivatives of a
function of the free energy. Equation (2.5) implies that, in any state of the
thermoelastic solid, the heat flux vector q cannot make an obtuse angle with
the temperature gradient
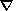 q.
q.
The internal dissipation
in the thermoelastic material is written as
Henceforward a colon in formulas means a double scalar product such that
A: B = AijBij.
On the strength of (2.3) and (2.4), this yields, i.e. the
thermoelastic medium is a perfect material in the sense that any smooth deformation
process is
not accompanied by internal dissipation. This only true of smooth flows. If a
particle crosses a strong discontinuity surface, its entropy can undergo a jump
at the shock wave due to the action of singular sources of entropy on the wave surface
[Landau and Lifshits, 1988].
The requirement of the material independence of the reference system choice (the
objectivity principle) leads to the following restraints on the constitutive
equations of a thermoelastic material:
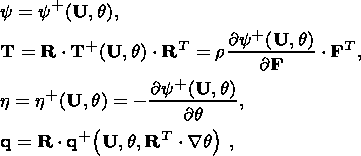 | (2.6) |
where R and U are the tensors in polar decomposition (2.1). I emphasize
that
relations (2.6) hold in a medium of an arbitrary type of symmetry.
A solid, initially isotropic thermoelastic material is particularly important in
applications. The constitutive relations of such a material, written through
kinematic quantities measured from the undistorted configuration of the body
k0, are invariant under the group of
proper orthogonal transformations of this
configuration. The free energy
y+ ( U, q)
and the heat flux vector
q+ ( U, q, RT
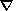 q)
in such a
material are isotropic functions obeying the identities
q)
in such a
material are isotropic functions obeying the identities
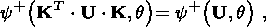 |
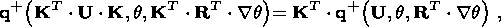 |
where
K is any orthogonal tensor with a positive determinant. Then, the
constitutive equations of a solid, initially isotropic thermoelastic material
can be written in the form
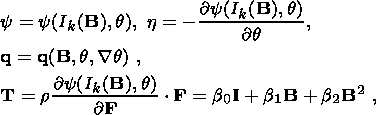 | (2.7) |
where
B = F  FT
= V2 is the symmetrical, positively definite tensor of
finite strain, and
Ik ( B), k = 1, 2, 3, are principal invariants
of
B determined
by the formulas
FT
= V2 is the symmetrical, positively definite tensor of
finite strain, and
Ik ( B), k = 1, 2, 3, are principal invariants
of
B determined
by the formulas
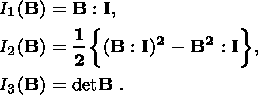 | (2.8) |
The scalar coefficients
bi = bi
(Ik, q),
i = 0, 1, 2;
k = 1, 2, 3 in the
polynomial representation of the Cauchy stress tensor T are functions of
temperature and invariants of the strain tensor B. These coefficients are
completely determined by the thermodynamic potential:
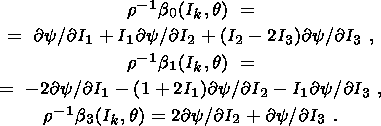 | (2.9) |
The complete system of equations of the thermoelastic material in regions of the
smooth solution in the Eulerian variables ( x, t ) can be written as a system of
divergent differential equations (local conservation laws):
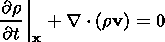 | (2.10) |
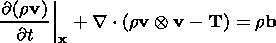 | (2.11) |
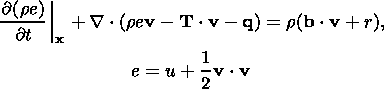 | (2.12) |
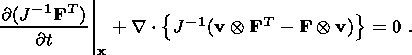 | (2.13) |
Henceforward,
J = det F, the symbol
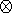 means the tensor product,
u is the
internal energy density,
e = u + 1/2 v
means the tensor product,
u is the
internal energy density,
e = u + 1/2 v  v is the total energy of unit mass,
b is the density of body forces and
r is the heat source distribution density. Relations
(2.10), (2.11) and (2.12) are, respectively, equations of the local mass
balance, motion and local energy balance. Equation (2.13) is a kinematic
relation ensuring the compatibility of deformations and velocities of a material
particle. System (2.10)-(2.13) is complemented by constitutive relations (2.6)
specifying the properties of the thermoelastic material.
v is the total energy of unit mass,
b is the density of body forces and
r is the heat source distribution density. Relations
(2.10), (2.11) and (2.12) are, respectively, equations of the local mass
balance, motion and local energy balance. Equation (2.13) is a kinematic
relation ensuring the compatibility of deformations and velocities of a material
particle. System (2.10)-(2.13) is complemented by constitutive relations (2.6)
specifying the properties of the thermoelastic material.
I should also note that the representation of a complete system of equations of
a thermoelastic body through local conservation laws (2.10)-(2.13) is possible
because the kinematic compatibility equation (2.13) connecting the variation
rate of the tensor F with the velocity gradient of a material particle was
used
in conjunction with the traditional conservation laws. This equation for a
nonsymmetric tensor F characterizing both the extension of a material element
and its rigid rotation as a whole has a divergent form in the case of arbitrary
deformations. Contrary to (2.13), kinematic relations of the type
that connect the total derivative of the Almansi finite strain tensor
E = 12( I - F-1T  F-1) (or another symmetric strain tensor) with the
velocity gradient are basically
irreducible to the divergent form. A more detailed discussion of this problem
can be found in
[Kondaurov, 1981;
Kondaurov and Nikitin, 1990].
F-1) (or another symmetric strain tensor) with the
velocity gradient are basically
irreducible to the divergent form. A more detailed discussion of this problem
can be found in
[Kondaurov, 1981;
Kondaurov and Nikitin, 1990].
The requirement of correctness of boundary problems involving system (2.10)-(2.13),
(2.6) imposes additional restraints on the free energy density
y ( F, q).
In the isothermal approximation, the necessary condition related to the
solvability of equilibrium problems for a thermoelastic body has the form
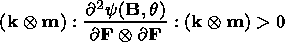 | (2.14) |
for arbitrary vectors
k 0, m 0. This inequality is called the strong
ellipticity condition
[Lurye, 1980;
Truesdell, 1972].
In the Lagrangian (substantial) variables ( X, t ) the system of differential
equations for a thermoelastic material can be written as
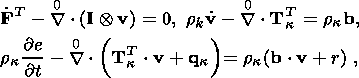 | (2.15) |
where
rk
is the mass density in the reference configuration
k connected with the
density
r in the actual configuration through the relation
 | (2.16) |
qk = J F-1
 q is the heat flux vector in the Lagrangian
variables
X, and
q is the heat flux vector in the Lagrangian
variables
X, and
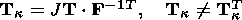 | (2.17) |
is the nonsymmetric Piola-Kirchhoff stress tensor of first kind.
3. Relations at the Interface
Here, based on the assumption that the process under study is close to the
mechanical and thermal equilibrium, I discuss the conditions on the moving
surface of a strong discontinuity separating two phases of a thermoelastic body
experiencing finite deformations and arbitrary heating. In the general case the
phases are assumed to be anisotropic solids with various types of anisotropy.
Then, for each phase there exists an undistorted reference
k(n)0, n =
1, 2, such
that the symmetry groups of the phase material
g(n)0 belong to a proper orthogonal
group
[Lurye, 1980;
Truesdell, 1972].
In other words, constitutive equations (2.6) of the phase material written in terms
of strains measured from the undistorted reference configurations are invariant under
orthogonal transformations belonging to
g(n)0.
The configurations
k(n)0 generally differing
in the density of material are
interrelated via the nondegenerate transformation
where a positively definite tensor
U0 is the gradient of the nondegenerate
mapping
k(2)0  k(1)0, and
d X(n) are the radius vectors connecting two infinitely
near material particles in the configurations
k(n)0. The value
U0 interrelating
undistorted reference configurations of an infinitely small material element in
different phase states depends on the temperature
q(n)0 and the stress
state
T(n)0 of the material in the configuration
k(n)0, i.e.
U0 = U0 ( T(n)0,
q(n)0).
Natural configurations in which stresses vanish and the temperature
q0 is constant are most widespread
in applications. The tensor
U0 is the kinematic characteristic of a phase transition
in solids. In the classical theory of phase transitions, an analog
of
U0 is the ratio of phase densities.
k(1)0, and
d X(n) are the radius vectors connecting two infinitely
near material particles in the configurations
k(n)0. The value
U0 interrelating
undistorted reference configurations of an infinitely small material element in
different phase states depends on the temperature
q(n)0 and the stress
state
T(n)0 of the material in the configuration
k(n)0, i.e.
U0 = U0 ( T(n)0,
q(n)0).
Natural configurations in which stresses vanish and the temperature
q0 is constant are most widespread
in applications. The tensor
U0 is the kinematic characteristic of a phase transition
in solids. In the classical theory of phase transitions, an analog
of
U0 is the ratio of phase densities.
Various configurations
k(n)0 differ not
only in the mass density and anisotropy
properties of the material but also in its free energy and entropy. In the case
of a single-phase medium, these thermodynamic potentials in the reference state
are usually set equal to constants of minor importance (most often to zero). In
phase transformations the difference between the free energies of phases in the
configurations
k(n)0, n =
1, 2, is a fundamental value, and it is natural to call
it the rheological characteristic of the first-order phase transition in solids.
The same is true of the entropy density. Rheological characteristics, as well as
the kinematic quantity
U0, depend on the initial temperature and initial
stresses in the configurations
k(n)0.
Now I formulate the relations on the moving surface of a strong discontinuity
(in crossing this surface, particles experience a phase transformation). Two of
these relations are obvious, namely, the temperature continuity condition
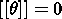 | (3.1) |
and the continuity condition of the radius vector
x determining the spatial
position of the material particle under study at the current time moment
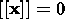 | (3.2) |
Actually, a discontinuity of the temperature
q or the vector
x at the moving
interface necessarily leads to infinite gradients of the temperature and
velocity vector arising when a particle crosses a strong discontinuity surface.
This is at variance with the assumption that the conditions of the phase
transformation are close to the equilibrium state.
Condition (3.2) is sometimes regarded as the definition of coherent (or
martensite) phase transitions. Examples of such transitions are provided by
twinning processes in crystals
[Coe, 1970;
Robin, 1974]
and some phase transformations in iron. Some authors
[Grinfeld, 1990;
Truskinovskii, 1983]
also discuss models of incoherent phase transformations or transitions with slip
in
which the normal component alone of the vector
x is continuous. Incoherent
transitions cannot be realized within the framework of a consistent quasi-thermostatic
model with a moving phase boundary, because such a transition
should be associated with an infinite values of the tangential component of the
velocity vector, implying an appreciable inertia effect. Slip motions are only
possible on a stationary surface which is a contact discontinuity surface not
crossed by particles. Attempts at the variational description of incoherent
phase transitions
[Grinfeld, 1990;
Truskinovskii, 1983]
employ the assumption on a class of admissible variations, which is unacceptable
for
moving phase boundaries.
In order to derive relations for other quantities at a strong discontinuity
surface, I use the material variables
X  X(1)
X(1) 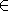 k(1)0
k(1)0  k of the undistorted reference configuration
of the body in the first phase state with the
temperature
q0. This means that the deformations
of the second phase are also
described in terms of the initial configuration
k. If the phases have the same
type of symmetry, the configuration
k is an undisturbed configuration for the
second phase. If the phases have different types of symmetry, the material of
the second phase in the configuration
k should have a symmetry group defined by
Noll's rule
[Truesdell, 1972].
The integral balance equation in these variables
has the form
k of the undistorted reference configuration
of the body in the first phase state with the
temperature
q0. This means that the deformations
of the second phase are also
described in terms of the initial configuration
k. If the phases have the same
type of symmetry, the configuration
k is an undisturbed configuration for the
second phase. If the phases have different types of symmetry, the material of
the second phase in the configuration
k should have a symmetry group defined by
Noll's rule
[Truesdell, 1972].
The integral balance equation in these variables
has the form
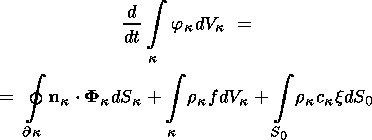 | (3.3) |
and includes relations (2.15) written in the integral form,
the strain-velocity compatibility equation, the equilibrium equation obtained
from equations of motion (2.15) by ignoring its inertia term, and the entropy
balance equation corresponding to the Clausius-Duhem inequality. Integral
equation (3.3) accounts for the presence of a strong discontinuity surface
S0 (t) moving at a velocity
ck in the direction of the normal
nk,
because this surface can contribute to the balance relation. The vectors in (3.3)
are
defined by the expressions
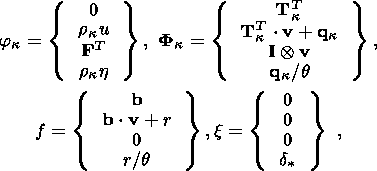 | (3.4) |
where
x is the vector of singular sources of the
d function type, with its carrier concentrated
on the surface
S0 (t).
Like in the classical theory of shock waves, I assume that no singular sources
of mass, momentum and energy are present on moving surfaces of strong
discontinuities separating two phases. As shown below, the absence of strain
incompatibility sources is ensured by continuity condition (3.2) imposed on the
displacement vector. As regards a singular source of entropy
d ,
the
case
d
,
the
case
d =0
corresponds, by definition, to a reversible phase transformation
and the case
d
=0
corresponds, by definition, to a reversible phase transformation
and the case
d >0,
to an irreversible phase transformation. The set of assumptions on
amplitudes of these sources within the framework of the system of conservation
laws is an independent part of any continuum model admitting discontinuous solutions
[Kulikovskii and Sveshnikova, 1998;
Sedov, 1970].
As is demonstrated by the solution of the problem on the shock wave structure in
an ideal gas
[Ovsyannikov, 1981;
Rozhdestvenskii and Yanenko, 1978],
the correctness of assumptions on the amplitudes and types of sources functioning
on strong
discontinuities can sometimes be demonstrated by invoking more general models in
which a strong discontinuity is modeled by a region of large gradients of the
solution and by passing to the model with a discontinuous solution as a limit.
Apparently, such a substantiation of first-order phase transition models in
solids has not been given.
>0,
to an irreversible phase transformation. The set of assumptions on
amplitudes of these sources within the framework of the system of conservation
laws is an independent part of any continuum model admitting discontinuous solutions
[Kulikovskii and Sveshnikova, 1998;
Sedov, 1970].
As is demonstrated by the solution of the problem on the shock wave structure in
an ideal gas
[Ovsyannikov, 1981;
Rozhdestvenskii and Yanenko, 1978],
the correctness of assumptions on the amplitudes and types of sources functioning
on strong
discontinuities can sometimes be demonstrated by invoking more general models in
which a strong discontinuity is modeled by a region of large gradients of the
solution and by passing to the model with a discontinuous solution as a limit.
Apparently, such a substantiation of first-order phase transition models in
solids has not been given.
System (3.3) yields the relations for discontinuities
at the phase boundary:
where
[[a]] = a+ - a- is the jump of a quantity
a at the strong discontinuity
surface, and its element under consideration is characterized by the normal
nk and
by the velocity along this normal
ck. Using expressions (3.4),
these relations
are written as,
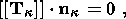 | (3.5) |
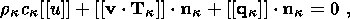 | (3.6) |
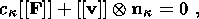 | (3.7) |
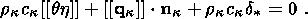 | (3.8) |
Relation (3.5) is the continuity condition of the stress vector at the
phase boundary and is an analogue of the pressure continuity condition at the
contact surface of liquid or gas phases. Relation (3.7) results from the
continuity of the vector
x( X, t) at the phase boundary and, apart from a dyadic
structure of the tensor
[[ F]], indicates the absence of a singular source of
incompatible strains and velocities. Actually, condition (3.2) ensures the
continuity of the vector
d x, which is an image of the substantial vector
d X 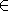 S0, i.e.
[[d x]] = [[ F]]
S0, i.e.
[[d x]] = [[ F]]  d
X = 0. Since
d X is arbitrary, this yields
d
X = 0. Since
d X is arbitrary, this yields
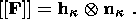 | (3.9) |
On the other hand, let
x be a point of a strong discontinuity surface
moving at a
velocity
ck in the direction of the normal
nk. Then,
 X/
X/ t|x = ck
nk and the
continuity of
x = x ( X (x, t),
t) yields
t|x = ck
nk and the
continuity of
x = x ( X (x, t),
t) yields
Using (3.9), I obtain
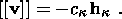 | (3.10) |
As seen from (3.9), the tensor
[[ F]] is a dyad, and the equality (3.7) follows from (3.9) and
(3.10). Using (3.10) and the relation
[[ab]] = 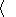 a
a 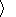 [[b]] + [[a]]
[[b]] + [[a]] 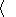 b
b
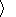 ,
where
,
where
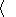 a
a 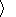 = 12 (a+ + a-), energy equation (3.6)
can be written in the form
= 12 (a+ + a-), energy equation (3.6)
can be written in the form
Based on the continuity of the stress vector, this expression is transformed into
the following:
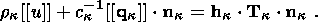 | (3.11) |
Equation (3.8) yields the normal component of the heat flux vector
substituting this expression into (3.11) and using the formula
y = u - qh and the
temperature continuity condition at the interface, I obtain
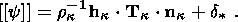 | (3.12) |
Equation (3.12) shows that the free energy density jump associated with the
phase transformation of a thermoelastic material is equal to the sum of the
dissipation
d and the work of the stress vector
rk-1
hk
and the work of the stress vector
rk-1
hk  Tk
Tk  nk on the strong discontinuity
considered. Scalar equality (3.12) is an analogue of the
equality condition of chemical potentials in the classical theory of the phase
equilibrium of a perfect liquid (gas)
[Gibbs, 1906;
Landau and Lifshits, 1964];
however, they basically differ from each other because (3.12) is a continuity
condition imposed on the normal components of the chemical potential tensor:
nk on the strong discontinuity
considered. Scalar equality (3.12) is an analogue of the
equality condition of chemical potentials in the classical theory of the phase
equilibrium of a perfect liquid (gas)
[Gibbs, 1906;
Landau and Lifshits, 1964];
however, they basically differ from each other because (3.12) is a continuity
condition imposed on the normal components of the chemical potential tensor:
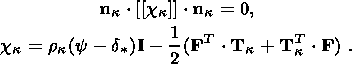 | (3.13) |
The equivalence of (3.12) and (3.13) can easily be shown taking into
account the formula
resulting from the definition of the
hk value and the relation
In relation to reversible phase transformations ( d = 0 ), the tensor
ck
was considered in works
[Bowen, 1964;
Grinfeld, 1990;
Kondaurov and Nikitin, 1983;
Mukhamediev, 1990;
Truskinovskii, 1983]
and is called the Lagrangian tensor of the chemical potential. The integral mass
balance relation
in the Eulerian variables has the form
= 0 ), the tensor
ck
was considered in works
[Bowen, 1964;
Grinfeld, 1990;
Kondaurov and Nikitin, 1983;
Mukhamediev, 1990;
Truskinovskii, 1983]
and is called the Lagrangian tensor of the chemical potential. The integral mass
balance relation
in the Eulerian variables has the form
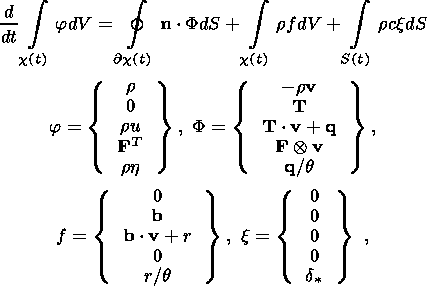 | (3.14) |
and includes integral continuity equation (2.10), the equilibrium
equation ensuing from equation of motion (2.11), energy
conservation law (2.12) in which the kinetic energy is ignored, strain-velocity
compatibility equation (2.13), and the entropy rate equation. Here
S(t) is the
interface moving at the velocity
c = D - v  n relative
to material
particles,
D is the velocity of
S(t) relative to the reference system and
n is the normal to the moving interface in a current configuration.
Equation
(3.14) yields the system of relations for jumps at a strong discontinuity surface
n relative
to material
particles,
D is the velocity of
S(t) relative to the reference system and
n is the normal to the moving interface in a current configuration.
Equation
(3.14) yields the system of relations for jumps at a strong discontinuity surface
In the developed form, this system is written as
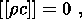 | (3.15) |
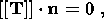 | (3.16) |
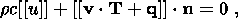 | (3.17) |
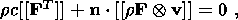 | (3.18) |
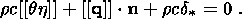 | (3.19) |
Relation (3.15) is a consequence of the continuity equation and represents
the continuity condition of the mass flux. Equality (3.16), resulting from the
equilibrium equation, is the continuity condition imposed on the stress vector
and written in terms of the symmetrical Cauchy stress tensor.
The Piola identity
[Lurye, 1980] yields
providing
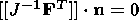 | (3.20) |
on the strong discontinuity surface. Equation (3.18) can be written in the
form
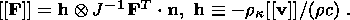 | (3.21) |
Taking into account the continuity of the stress vector and
expression (3.21) for the strain gradient jump, equality (3.17) is reduced to
the form
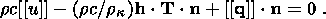 | (3.22) |
Expressing with the help of (3.19) the jump in the normal
component of the heat flux vector through the entropy jump and the dissipation
density
d and substituting the result into (3.22), one obtains equation the
equality equivalent to (3.12)
and substituting the result into (3.22), one obtains equation the
equality equivalent to (3.12)
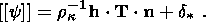 | (3.23) |
Equation (3.23) can also be written in
terms of the convolution of a second-rank tensor with the normals
n. To
demonstrate this, I multiply (3.23) by the scalar
which is, due to (3.20), continuous at the strong discontinuity surface. As a result,
I obtain
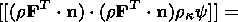 |
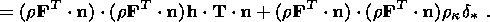 |
Taking into account the definition of the vector
h in (3.21) implying that
the equality
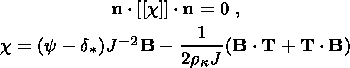 | (3.24) |
is obtained for normal components of the tensor
c, which may be called the tensor
of Eulerian chemical potential. Using formula (2.17) it is easy to obtain the
relation between the tensors
c and
ck
demonstrating the equivalence of the spatial (Eulerian) and substantial
(Lagrangian) descriptions of phase transitions in nonlinear elastic media.
Note that the dissipation
d entering in conditions (3.12) and (3.23) and
accounting for the effect of a singular entropy source on the interface provides
a means for a natural description of the hysteresis phenomenon associated with
the difference between thermodynamic conditions at which direct and reverse
phase transitions of the first order take place in solids. Relation (3.12)
yields
entering in conditions (3.12) and (3.23) and
accounting for the effect of a singular entropy source on the interface provides
a means for a natural description of the hysteresis phenomenon associated with
the difference between thermodynamic conditions at which direct and reverse
phase transitions of the first order take place in solids. Relation (3.12)
yields
where
qd and
qr are the temperatures of direct
and reverse phase transitions,
and
y(1) and
y(2) are free energies of the first
and second phases. Adding these
two equalities shows that
qd>qr
if
y(2) (q)
in the temperature interval
considered increases more rapidly than
y(1) (q).
A recrystallization process plays a particular role among phase transitions in
solids. This phenomenon relates to anisotropic solids and is a particular case
of a phase transition when the initial and newly formed phases consist of the
same material whose particles, when crossing the interface, undergo a finite
deformation and a finite rotation changing the spatial orientation of anisotropy
axes. Some authors
[Grinfeld, 1990]
define recrystallization as "a process
changing all of the nearest neighbors of material particles," implying that the
mapping of the reference configuration onto the actual configuration is no
longer a one-to-one mapping. As before, in this case attempts to analyze
incoherent phase transitions in terms of the quasi-thermostatic model of a
thermodynamic body encounter the problem of high tangential accelerations of a
material particle arising when it crosses a moving interface on which slip
motions changing neighbors take place. In my opinion. such a definition is
hardly suitable for the formulation and analysis of problems involving movable
phase boundaries.
I should note that the requirement of a finite deformation accompanying a finite
rotation of particles is essential for the recrystallization definition used
here. Actually, let rotations of particles be finite and let deformations be
small, i.e. the tensor
F has the form
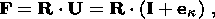 |
where
ek is a tensor of small strain
of the order of
O(d) with a small
parameter
d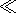 1, and
R is an orthogonal tensor of finite rotation. Then,
accurate to the terms
O(d2), the value
B is determined by the expression
1, and
R is an orthogonal tensor of finite rotation. Then,
accurate to the terms
O(d2), the value
B is determined by the expression
where
e = R  ek
ek
 RT is the strain tensor
of the
order
O(d). Using relation (3.21) for the strain
gradient jump and the formula
[[ab]] = a [[b]] + [[a]] b + [[a]] [[b]],
I obtain
RT is the strain tensor
of the
order
O(d). Using relation (3.21) for the strain
gradient jump and the formula
[[ab]] = a [[b]] + [[a]] b + [[a]] [[b]],
I obtain
Taking into account that
J = det F = 1 + I1 ( e) + O (d2),
F  FT =
I + 2 e this relation can be reduced to
the form
FT =
I + 2 e this relation can be reduced to
the form
Since the left-hand side and two terms on the right of this equation are of the
order
O(d), the third term on the right must have
the same order:
This gives the relations
The second equation has the solutions
( h  n) = O (d)
and
( h
n) = O (d)
and
( h  n) = -2 + O (d). Substituting
the solution
h
n) = -2 + O (d). Substituting
the solution
h  n = O (d)
into the first equation gives the value
h = O(d) corresponding to a small
jump in the rotation of a material element
at the phase boundary. The solution
( h
n = O (d)
into the first equation gives the value
h = O(d) corresponding to a small
jump in the rotation of a material element
at the phase boundary. The solution
( h  n) = -2 + O (d) describes
a finite rotation jump, but this
solution is unacceptable because formula (3.20), which is a consequence of the
Piola identity, yields
[[ FT]]
n) = -2 + O (d) describes
a finite rotation jump, but this
solution is unacceptable because formula (3.20), which is a consequence of the
Piola identity, yields
[[ FT]]  n =
O(d) if the relation
F = R
n =
O(d) if the relation
F = R  U = R
U = R  ( I + ek)
is taken into account. Hence, I obtain
( I + ek)
is taken into account. Hence, I obtain
The vector
FT  n is not
identically zero, because otherwise a nontrivial
solution of the homogeneous nondegenerate linear system
FT
n is not
identically zero, because otherwise a nontrivial
solution of the homogeneous nondegenerate linear system
FT  n = 0,
det F 0, should exist, implying that
( h
n = 0,
det F 0, should exist, implying that
( h  n) = O(d);
i.e. the theory of recrystallization is necessarily a finite strain theory.
n) = O(d);
i.e. the theory of recrystallization is necessarily a finite strain theory.
4. Clapeyron-Clausius Equations
I consider the system of equations consisting of the condition of stress vector
continuity (3.5) and free energy jump condition (3.12):
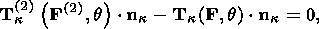 |
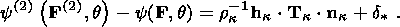 |
The superscript "2" indicates here values characterizing the second phase, and
the first phase is not indexed for brevity. With regard for dyadic form (3.9) of
the jump
[[ F]] and temperature ( q ) continuity condition (3.1), this system
can be written in the form
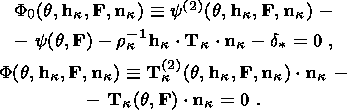 | (4.1) |
With given values of
F and
nk, relation (4.1) can be regarded
as a system of
scalar and vector equations determining the temperature
q and the vector
hk.
Using relation (2.6), which connects the stress tensor and entropy density with
the free energy function, and the formula
 F(2)ij/
F(2)ij/ hka
= diankj
resulting from (3.9), the necessary condition of the solvability of such a system
can be written as
hka
= diankj
resulting from (3.9), the necessary condition of the solvability of such a system
can be written as
This condition holds true if strong ellipticity condition (2.14) is valid for the
newly formed phase and if
M 0. System (4.1) implies that the temperature
q of
a quasi-static phase transition in a thermoelastic material is a function of the
deformation of the initial phase and orientation of the interface:
This circumstance determines the basic distinction of phase transitions in a solid
from those in an ideal liquid, in which the melting (evaporation) temperature
depends on the pressure alone and is determined by the Clapeyron-Clausius equation
[Landau and Lifshits, 1964]:
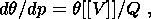 | (4.2) |
where
Q = q [[h]]
is the phase transition heat and
[[V]] the jump of the specific volume
V = 1/r. An analogue of (4.2) in a thermoelastic
body is the equation
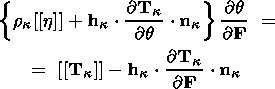 | (4.3) |
describing the differential
dependence of the phase transition temperature on the initial phase strain F
with a fixed normal
nk to the interface.
To derive this equation, I differentiate the first equation in (4.1) with
respect to F at
nk = const. Since
hk = hk
( F, nk),
q = q ( F,
nk),
I obtain
Formulas (2.6) and (2.17), stress vector continuity condition (3.5) and the formula
resulting from (3.9) provide the sought-for equation (4.3).
Another equation, representing a new relation in the theory of phase transformations
in continua
and determining the differential dependence of the phase transition temperature
on the interface orientation at a fixed strain of the initial phase F, has
the
form
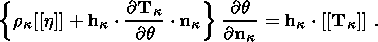 | (4.4) |
Relation (4.4) is obtained by differentiating the first equation in
system (4.1) with respect to the vector
nk at a fixed value of the
tensor
F.
Taking into account (2.6) and (2.17), this yields
Using condition (3.5) and the equality
 F(2)ij/
F(2)ij/ nka
= hkidaj
+ nka
nka
= hkidaj
+ nka hki/
hki/ nka
resulting
from (3.9). The equation in question is obtained.
nka
resulting
from (3.9). The equation in question is obtained.
Equations (4.3) and (4.4) hold in a
thermoelastic material with an arbitrary type of symmetry. Now I address a
thermoelastic material both phases of which are initially isotropic. The
kinematic characteristic of a phase transition
U0 in such a material is an
isotropic tensor determined by the ratio of phase densities in natural
configurations at a temperature
q0. In this case, symmetry groups of
the
initial and newly formed phases in the natural initial state coincide with the
proper orthogonal group. The reference configurations
k are undistorted for both
phases; these are the natural configuration for the first phase and a
configuration characterized by an initial isotropic stress tensor for the second
phase. The constitutive equations can be written as relations (2.7).
Equation (4.3) containing nine independent components
 q/
q/ F is reduced in the medium under consideration to a symmetrical
tensor equation for the derivative
F is reduced in the medium under consideration to a symmetrical
tensor equation for the derivative
 q/
q/ B, and relation (4.4) is transformed into an equation for the
derivative
B, and relation (4.4) is transformed into an equation for the
derivative
 q/
q/ n.
This statement becomes evident if one considers, rather than system (4.1),
stress vector continuity condition (3.16) and energy jump relation (3.23) in the
Eulerian variables:
n.
This statement becomes evident if one considers, rather than system (4.1),
stress vector continuity condition (3.16) and energy jump relation (3.23) in the
Eulerian variables:
This immediately implies that the phase transition
temperature is
q = q ( B,
n).
In order to write equations (4.3) and (4.4) in the Eulerian
variables, the following relations resulting from formulas (3.9) and (3.21) are
utilized:
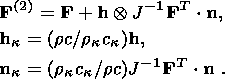 | (4.5) |
Using (4.5) and relations (2.17) between the Cauchy and Piola-Kirchhoff
stress tensors, equation (4.4) can be written in the form
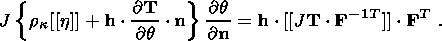 |
Taking into account
formula (3.21) for a jump in the tensor
F and the continuity of the stress
vector, the right-hand side of this equation can be transformed as follows:
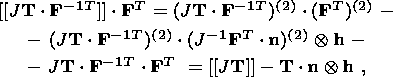 | (4.6) |
which finally yields
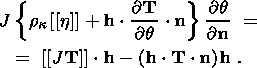 | (4.7) |
In the classical case of the phase equilibrium of an ideal liquid with the
stress tensor
T = -p (V, q) I,
V = J/rk
= 1/r,
the derivative
 q/
q/ n is identically zero.
Actually, due to the continuity of pressure at the interface, the right-hand
side of equation (4.7) is written in this case as
p( h
n is identically zero.
Actually, due to the continuity of pressure at the interface, the right-hand
side of equation (4.7) is written in this case as
p( h  n - [[J]])
h.
This value vanishes because condition of the mass flux continuity (3.15) implies
that
n - [[J]])
h.
This value vanishes because condition of the mass flux continuity (3.15) implies
that
Taking into account the second formula in (3.21), I obtain
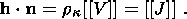 | (4.8) |
This immediately proves the above statement.
If both phases of an initially isotropic thermoelastic
material are solid, an interface orientation providing an extremum of the phase
transformation temperature exists at a fixed strain state of the initial phase.
This extreme value is attained if one of the principal axes of the finite strain
tensor
B (or any other tensor coaxial with
B ) coincides with the normal
n to the interface. Actually, let
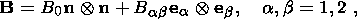 | (4.9) |
where
ea are unit vectors of the
principal
axes of the tensor
B that lie in the plane tangent to the interface. On the
strength of polynomial representation (2.7), the Cauchy stress tensor of an
initially isotropic medium has the same structure:
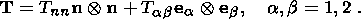 | (4.10) |
As follows from the continuity of the stress vector
[[ T]]  n = 0,
the Cauchy stress tensor has the same
structure in the second phase as well:
n = 0,
the Cauchy stress tensor has the same
structure in the second phase as well:
In materials with a one-to-one
correspondence between the tensors
T(2) and
B(2), this yields
Hence,
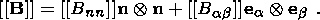 | (4.11) |
For the strain state under consideration, the first relation in (4.5)
yields
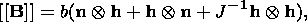 |
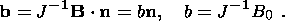 |
Representing the vector
h as the sum of normal and tangential
components,
and substituting it into the preceding relation, I find
Comparison of this formula with (4.11) shows that
h = h n, where
h = rk
[[V]] = [[J]] due to (4.8). This also yields
[[Bab]]
= 0,
i.e. all components of the tensor B, except
for the normal component
Bnn, are continuous at the interface. I emphasize
that the continuity of the components
Bab
is valid for the state (4.9)
considered, but they are discontinuous in the general case.
The substitution of the vector
h= h n into (4.7) makes the derivative
 q/
q/ n equal to zero, which
corresponds to a phase transition temperature extremum in deformed state (4.9).
n equal to zero, which
corresponds to a phase transition temperature extremum in deformed state (4.9).
If the phase is a thermoelastic liquid, its constitutive equations are
invariant under unimodular (not changing the density) transformations of the
reference configuration. I.e. in considering a solid-liquid phase transition,
one may always assume, without loss of generality, that
h = h n, which makes
the derivative
 q/
q/ n equal to zero. In other words, if one of the phases of
an
initially isotropic nonlinear elastic material is a liquid, the phase transition
temperature does not depend on the orientation of the interface. This statement
justifies, to an extent, the applicability of the classical theory to the
description of melting in solids and shows that solid effects affect only
slightly the pattern of this process.
n equal to zero. In other words, if one of the phases of
an
initially isotropic nonlinear elastic material is a liquid, the phase transition
temperature does not depend on the orientation of the interface. This statement
justifies, to an extent, the applicability of the classical theory to the
description of melting in solids and shows that solid effects affect only
slightly the pattern of this process.
The equation determining the phase transformation temperature as a function of the
extension of the initial phase
has the form
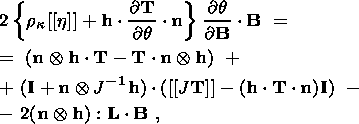 | (4.12) |
where
L =  T/
T/ B is the fourth-rank tensor of elastic
moduli.
B is the fourth-rank tensor of elastic
moduli.
Equation (4.12) is derived as follows. Using (4.5) and substituting the
relation
Tk = J T  F-1T between the stress
tensors into (4.3), I obtain
F-1T between the stress
tensors into (4.3), I obtain
The derivative of the phase transition temperature with respect to the tensor
F
at
nk = const is
In deriving this equation, I used the formula
 F-1Tis/
F-1Tis/ Fab = - F-1Tib
F-1Tas obtained by differentiating the
identity
F-1si Fik = dsk
with respect to
Fab.
Substituting this expression into the preceding relation gives the
equation
Fab = - F-1Tib
F-1Tas obtained by differentiating the
identity
F-1si Fik = dsk
with respect to
Fab.
Substituting this expression into the preceding relation gives the
equation
Writing out the derivative in the last term, taking into account the
formulas
and scalarly multiplying the equation to the right by the tensor
FT,
I obtain
Using formula (4.6) and collecting similar terms yield the desired
equation (4.12).
In the case of deformed state (4.9) with the shear strain and stress vanishing
on the interface, equation (4.12) is reduced to the two simpler relations
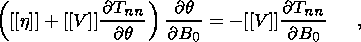 | (4.13) |
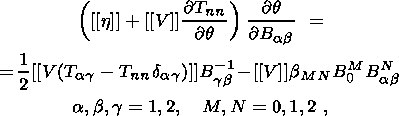 | (4.14) |
where
In order to demonstrate this, I note that formulas (4.10)
and (4.11) yield
Since
h = [[J]] n for the strain under consideration, I obtain
h  T
T  n = [[J]] Tnn. Hence,
the first term on the right-hand side of (4.12) is equal to
[[J (Tab
- dab Tnn)]] ea
n = [[J]] Tnn. Hence,
the first term on the right-hand side of (4.12) is equal to
[[J (Tab
- dab Tnn)]] ea 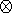 eb,
and the second term vanishes due to (4.9) and collinearity of the vectors h
and n.
The last term is equal to
eb,
and the second term vanishes due to (4.9) and collinearity of the vectors h
and n.
The last term is equal to
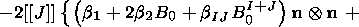 |
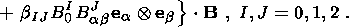 |
These expressions can be obtained by differentiating polynomial representation
(2.7) of the Cauchy stress tensor with due regard for definition (2.8) of the
principal invariants
Ik ( B),
k = 1, 2, 3, and the Hamilton-Cayley theorem
[Lurye, 1980]:
Since in the case of deformation (4.9) the value
(b1 + 2 b2
B0 + bIJ BI+J0)
is equal to
 Tnn/
Tnn/ B0, relations (4.13) and (4.14) are proven.
B0, relations (4.13) and (4.14) are proven.
5. Linear, Initially Isotropic Thermoelastic Material
As an example, also interesting on its own, I address the first-order phase
transition in an initially isotropic thermoelastic solid with small deformations
and small deviations of temperature from its initial value. Let
k be the
undistorted reference configuration of a material element in the initial phase
state. As a reference configuration of this element in the other phase state,
the same configuration
k, which will also be undistorted due to the isotropy
of
the medium, is used. The temperature of the material in
k is set equal to
q0 and its mass density is denoted as
rk.
The initial state of the first phase is
regarded as a natural (unstressed) one, and the second phase in the
configuration
k is characterized by an isotropic initial stress
state
T0 = - p0 I.
Deformations of each phase measured from the configuration
k and temperature
variations are set to be small. A constant singular source of entropy is
assumed. The free energy density is smooth in the vicinity of the initial state
of each phase and can then be written accurate to second-order terms in the form
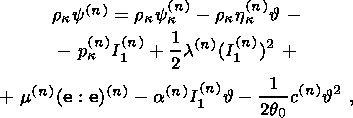 | (5.1) |
where
n = 1, 2, is the number of phase;
e is the small strain tensor;
I1 = I: e,
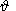 = q - q0,
= q - q0,
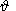 /q0
/q0
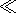 1; and the
coefficients
y(n)k,
p(n)k,
h(n)k,
c(n),
a(n),
l(n) and
m(n) are functions of the
temperature
q0. The entropy density and stress tensor
in such
a material are written in the form of linear relations:
1; and the
coefficients
y(n)k,
p(n)k,
h(n)k,
c(n),
a(n),
l(n) and
m(n) are functions of the
temperature
q0. The entropy density and stress tensor
in such
a material are written in the form of linear relations:
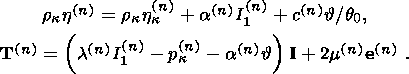 | (5.2) |
They suggest that
l(n) and
m(n) are the Lame coefficients,
a(n) is the thermal expansion
coefficient,
c(n) is the heat capacity,
and the values
y(n)k,
h(n)k
and
p(n)k characterize
the free energy, entropy and pressure in the initial states. I
assume
p(2)k = p0,
y(2)k
= y0,
h(2)k
= h0 and
p(1)k = y(1)k = h(1)k = 0. Relations (5.2) show that the
approximation of small deformations is valid if the initial pressure is small
compared to the elastic moduli.
As follows from second relation in (5.2), the jump in the stress tensor at the
interface has the form
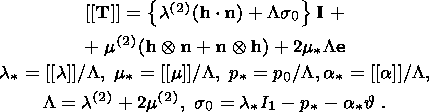 | (5.3) |
Using the stress vector continuity condition
[[ T]]  n = 0, I obtain
n = 0, I obtain
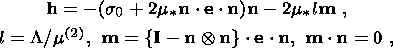 | (5.4) |
where
m is the component of the vector
e  n tangent to the interface.
n tangent to the interface.
Now I address relation (3.23) determining the jump in the free energy density;
for the subsequent analysis, (3.23) is convenient to use in the form
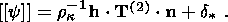 | (5.5) |
Taking into account the relations
and formula (5.4), equality is reduced to the form
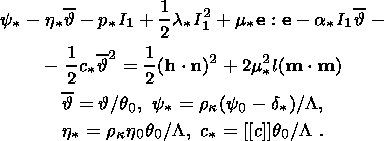 | (5.6) |
Taking into account expression (5.4) for the vector h, equation (5.6) implies
that, if the dimensionless entropy jump is
h = O(1), the phase transition
temperature is
= O(1), the phase transition
temperature is
i.e. it is only determined by the
y and
h
and
h values and by the dissipation
d
values and by the dissipation
d .
The incorporation of terms on the order of
O(d2) is unreasonable in
the approximation considered, because equations (5.2) are written accurate to
the terms of the second order of smallness.
.
The incorporation of terms on the order of
O(d2) is unreasonable in
the approximation considered, because equations (5.2) are written accurate to
the terms of the second order of smallness.
In the case
h = O(d) the phase transition temperature
appreciably depends on
the strain tensor of the initial phase and the orientation of the normal to the
interface relative to the principal axes of the tensor
e. Before examining this
dependence, note that the difference between thermoelastic coefficients of the
phases can be, generally speaking, rather large
[Babichev et al., 1991].
Therefore, I consider the following case:
= O(d) the phase transition temperature
appreciably depends on
the strain tensor of the initial phase and the orientation of the normal to the
interface relative to the principal axes of the tensor
e. Before examining this
dependence, note that the difference between thermoelastic coefficients of the
phases can be, generally speaking, rather large
[Babichev et al., 1991].
Therefore, I consider the following case:
In accordance with (5.3) and (5.5), the equation for the phase transition
temperature derivative with respect to the vector normal is written in this
approximation as
This implies, according to the general theory, that the phase transition
temperature at a fixed strain of the initial phase assumes an extreme value if
the normal to the interface coincides with a principal axis of the strain
tensor,
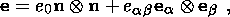 | (5.7) |
because
m = 0 at such a strain and therefore

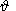 /
/ n = 0.
The type of the extremum is determined by the matrix
n = 0.
The type of the extremum is determined by the matrix
 2
2 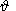 /
/ n
n 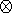
 n at strain (5.7).
n at strain (5.7).
The equation for the phase transition temperature derivative with respect to the
strain tensor is written as
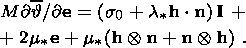 | (5.8) |
Equation (5.8) leads to an important general statement concerning the phase
transition pattern in the material considered: an increase in the volume strain
changes the type of the phase transformation in a linear thermoelastic solid, i.e.
a normal phase transition changes to an anomalous transformation and vice versa.
Of course, this refers to materials in which the phase transition is
accompanied by a change in the elastic moduli comparable with their values, and
the difference between the initial entropies is on the order of
h = O(d).
The aforementioned effect is solely due to the solid-state properties of the
material (the presence of a stress deviator and its effect on the equilibrium
state energy of the medium).
= O(d).
The aforementioned effect is solely due to the solid-state properties of the
material (the presence of a stress deviator and its effect on the equilibrium
state energy of the medium).
Actually, at a fixed normal and a constant intensity of shear strain,
I2 = ( e :
e
:
e )1/2 = const,
where
e
)1/2 = const,
where
e = e - 1/3
I1 I is the strain tensor deviator,
the phase transition temperature derivative with respect to the first invariant is
= e - 1/3
I1 I is the strain tensor deviator,
the phase transition temperature derivative with respect to the first invariant is
The right-hand side of this equation vanishes if the strain tensor component
normal to the phase boundary is connected with the two other diagonal components
through the relation
Such a strain tensor provides a phase transition temperature extremum with
respect to
I1. If the thermal expansion coefficients
a = O(d) differ only
slightly, this relation can be written, accurate to the first-order terms, in
the explicit form
= O(d) differ only
slightly, this relation can be written, accurate to the first-order terms, in
the explicit form
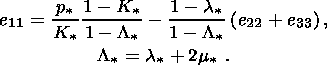 | (5.9) |
In the case of uniform extension (compression), when
the deviator
e vanishes, this relation
has a particularly simple form:
vanishes, this relation
has a particularly simple form:
In the general case, deformations providing an extremum of the phase transition
temperature are determined by the solution of the system consisting of equation
(5.9) and the condition
e : e
: e = const (a constant shear intensity).
= const (a constant shear intensity).
6. Effects of Stress Relaxation
Now I analyze, following the work
[Kondaurov and Nikitin, 1986],
some characteristics of phase transformations accompanied by stress relaxation in
the
solid phase. The solid phase is described in terms of the model of a
viscoelastic medium of the relaxation type. In this case, the state of a
material particle is determined by its deformation, temperature, temperature
gradient and viscous deformation, and the system of relations governing the
material response includes a viscous law in addition to expressions for the
thermodynamic potential, stress tensor and heat flux. Below I restrict myself to
the simplest case of an initially isotropic viscoelastic material of the solid
phase. Moreover, the medium is supposed to be a perfect, plastically
incompressible material. Such a model has the following implications. The
gradient
F of the transformation mapping a neighborhood of a material element
X from the initial configuration
k into the actual configuration
c(t) can be
represented as the composition
[Kondaurov and Nikitin, 1990;
Lee, 1969]
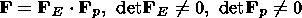 | (6.1) |
of the gradients of the nondegenerate transformations
k kp
( X, t) and
kp ( X, t)
kp
( X, t) and
kp ( X, t)  c (t) mapping
the
reference configuration
k into an intermediate (instantly unloaded)
configuration
kp ( X, t) which
in turn is mapped into
c (t).
The inelastic volume strain is
det Fp = 1. Rheological relations constituting a system
of equations
of state and kinetic equation of viscous deformations can be written in the form
c (t) mapping
the
reference configuration
k into an intermediate (instantly unloaded)
configuration
kp ( X, t) which
in turn is mapped into
c (t).
The inelastic volume strain is
det Fp = 1. Rheological relations constituting a system
of equations
of state and kinetic equation of viscous deformations can be written in the form
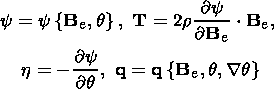 | (6.2) |
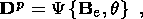 | (6.3) |
where
y { Be, q}
and
q { Be, q, 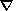 q} are isotropic
functions of the free energy
and heat flux vector;
q} are isotropic
functions of the free energy
and heat flux vector;
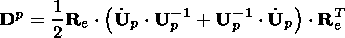 | (6.4) |
is the symmetrical tensor of viscous strain rate,
Be = V2e is the symmetrical,
positively definite tensor of elastic strain;
Ik ( Be),
k = 1, 2, 3, are the
principal invariants of the tensor
Be;
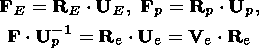 | (6.5) |
are the polar decompositions into orthogonal and symmetrical, positively
definite tensors, from which the following relations are derived using
composition (6.1):
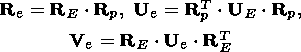 | (6.6) |
Constitutive equations (6.2)-(6.3) are necessary and sufficient in order that
(i) the Clausius-Duhem inequality hold true in all smooth processes of
deformation and temperature variation;
(ii) the equations be independent of the choice of the reference system;
(iii) the equations be invariant under orthogonal transformations of the
unloaded configuration
kp ( X, t) of
an infinitely small material element
X;
(iv) the equations be invariant under arbitrary unimodular transformations of
the initial configuration.
Since
Up is a symmetrical, positively definite tensor, relations
(6.3)-(6.4)
can be resolved with respect to
Up. This means that the flow law can be written
in the form
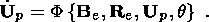 | (6.7) |
Relation (6.7) is the divergent equation describing the elastic strain variation
rate in the Lagrangian (material) variables
X. The divergent form of equation
(6.7) in the Eulerian (spatial) variables is
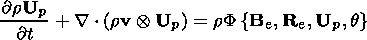 | (6.8) |
This equation is readily obtained by adding relation (6.7) multiplied by mass
density
r and continuity equation (2.10) multiplied by
the tensor
Up. Relation
(6.7) or (6.8) implies that
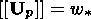 | (6.9) |
at the interface, which is a strong discontinuity surface; here
w is the
intensity of a singular source of inelastic deformations on the interface. This
value determines the jump in the viscous strain of a material particle crossing
the interface and is one of the factors controlling the stress drop associated
with the formation of a new phase and the value of the singular dissipation
source in equation (3.12). The value
w
is the
intensity of a singular source of inelastic deformations on the interface. This
value determines the jump in the viscous strain of a material particle crossing
the interface and is one of the factors controlling the stress drop associated
with the formation of a new phase and the value of the singular dissipation
source in equation (3.12). The value
w is one of rheological characteristics
that are preset in the model of the quasi-static phase transition in solids.
is one of rheological characteristics
that are preset in the model of the quasi-static phase transition in solids.
To illustrate the properties inherent in phase transformations during stress
relaxation in the solid phase, I consider the problem of melting of a
viscoelastic solid layer. Let an unstressed layer of a constant thickness
b occupy the region
0 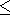 x
x 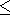 b
in the initial state (the axis
x = x1 is
perpendicular to the layer boundaries, and the axes
x2 and
x3 lie in the
boundary plane
x1 = 0 ). The temperature of the material
q0 is below the
melting temperature in the absence of stresses. The boundary
x = 0 is fixed and
its temperature is maintained constant and equal to
q0 at
t
b
in the initial state (the axis
x = x1 is
perpendicular to the layer boundaries, and the axes
x2 and
x3 lie in the
boundary plane
x1 = 0 ). The temperature of the material
q0 is below the
melting temperature in the absence of stresses. The boundary
x = 0 is fixed and
its temperature is maintained constant and equal to
q0 at
t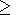 0. A constant
normal compressive stress
- s0,
s>0, is applied to the boundary
x = b at the time
t = 0, and the temperature of the medium increases to a value
q1 = const>0 at which a part of the
layer adjacent to the boundary
x = b melts.
The boundary of the melting region is found from the solution of the problem.
Mass forces and distributed heat sources are neglected.
0. A constant
normal compressive stress
- s0,
s>0, is applied to the boundary
x = b at the time
t = 0, and the temperature of the medium increases to a value
q1 = const>0 at which a part of the
layer adjacent to the boundary
x = b melts.
The boundary of the melting region is found from the solution of the problem.
Mass forces and distributed heat sources are neglected.
The temperature distribution in the solid phase and melt is assumed to be linear
across the layer:
This assumption implies that the heat conductivity of the material is so high
that the characteristic time of the temperature buildup is negligibly small
compared to the stress relaxation time.
I assume that deformations due to compression, heating and melting are small.
The solid phase is modeled by a homogeneous isotropic perfect viscoelastic
material with the density
rs and temperature
q0 in the natural initial
state
ks. The free energy density of
the solid phase occupying the region
0 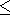 x
x 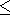 a(t)
can be written as
a(t)
can be written as
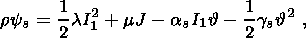 | (6.10) |
where
I1 = e(e)kk and
J = e(e)ij e(e)ij
are the first and second invariants of the elastic
strain tensor
e(e),
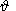 = q - q0,
= q - q0,
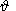 /q0
/q0
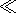 1, is the temperature variation,
l (q0)
and
m (q0)
are elastic moduli,
as (q0)
is the coefficient of thermal expansion, and
gs (q0)
is the heat capacity (accurate to the multiplier
q0 ). The difference between
the densities in the reference and actual configurations is ignored due to the
smallness of deformations. As follows from (6.10), the stress tensor and entropy
density in the solid phase have the form
1, is the temperature variation,
l (q0)
and
m (q0)
are elastic moduli,
as (q0)
is the coefficient of thermal expansion, and
gs (q0)
is the heat capacity (accurate to the multiplier
q0 ). The difference between
the densities in the reference and actual configurations is ignored due to the
smallness of deformations. As follows from (6.10), the stress tensor and entropy
density in the solid phase have the form
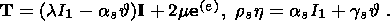 | (6.11) |
The complete strain tensor
e is the sum of the elastic ( e(e) )
and viscous ( e(p) ) strain tensors:
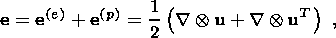 | (6.12) |
where
u is the vector of displacement from the initial state to the current
state.
The variation rate of the viscous strain
e(p) is determined by viscous flow law
(6.3); within the framework of the assumptions adopted, the latter reduces to
the relation
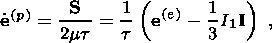 | (6.13) |
where
S = T - 1/3 ( T: I) I
is the stress tensor deviator
and
t (q0)
> 0 is the relaxation time.
The natural (unstressed) reference configuration
kf of the body in the liquid
state with the temperature
q0 is represented by a plane layer
of the density
rf. The phase density difference
is set to be small:
(rs - rf)/rs 1.
Due to the similarity between
rs and
rf, the melted layer thickness
bf = b (rs/rf)1/3 differs only slightly
from
b. Using the configuration
ks of the layer in the solid
state as
a reference configuration with initial stresses for the melt, the free energy
density of the liquid occupying the region
a (t)
1.
Due to the similarity between
rs and
rf, the melted layer thickness
bf = b (rs/rf)1/3 differs only slightly
from
b. Using the configuration
ks of the layer in the solid
state as
a reference configuration with initial stresses for the melt, the free energy
density of the liquid occupying the region
a (t)  x
x  b can be written as
b can be written as
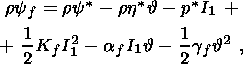 | (6.14) |
where
gf, af
and
Kf are functions of
q0, and the value
I1 = 1 - r/rs
determines the volume strain in the melt measured from the
configuration
ks. The value
y is the difference between the phase
potentials in the configuration
ks, and
T
is the difference between the phase
potentials in the configuration
ks, and
T = - p
= - p I is the tensor of "initial" stresses in the melt occupying
the region
ks.
If the initial density of the solid phase exceeds the melt density ( rs > rf),
we have
p
I is the tensor of "initial" stresses in the melt occupying
the region
ks.
If the initial density of the solid phase exceeds the melt density ( rs > rf),
we have
p > 0, i.e. the melt should be
compressed in order to make the solid
and liquid phase densities equal to each other, and vice versa,
p
> 0, i.e. the melt should be
compressed in order to make the solid
and liquid phase densities equal to each other, and vice versa,
p < 0 if
rs < rf.
The dependences of pressure and entropy density on mass density and
temperature of the melt as determined by (6.14) have the form
< 0 if
rs < rf.
The dependences of pressure and entropy density on mass density and
temperature of the melt as determined by (6.14) have the form
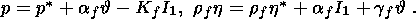 | (6.15) |
This implies that
Kf is the bulk modulus,
af is the thermal expansion
coefficient and
gf is the heat capacity of the
liquid phase (accurate to
the multiplier
q0 ).
Let
u(x, t) be the material particle displacement along the
x axis. All other
components of the displacement vector in both phases are set equal to zero.
Then, the nonzero component of the complete strain tensor is
The equilibrium equation
 p/
p/ x = 0 and the boundary condition
p (b, t) = s0
yield
x = 0 and the boundary condition
p (b, t) = s0
yield
Substituting this expression into the first formula in (6.15) and integrating in
x, I obtain
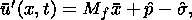 | (6.16) |
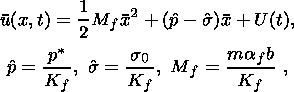 | (6.17) |
where
x = x/b and
u = u/b are the dimensionless coordinate and displacement,
and
U (t) is an unknown function of time determined from the solution
of the
problem. The free energy density of the melt is then reduced to the form
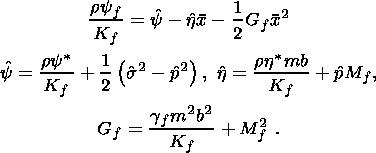 | (6.18) |
Now I consider the equations for the solid phase under conditions of the
uniaxial strain
where
e1 is the basis vector of the Cartesian coordinates
xi. Taking into
account the symmetry of the problem about the
x axis and the zero value of the
inelastic volume strain, the viscous strain tensor can be written as
and the elastic strain tensor, as
this yields
I1 = u and
J = (u
and
J = (u - 2p)2
+ 2p2. Given a uniaxial strain, free
energy density
(6.10) reduces to the form
- 2p)2
+ 2p2. Given a uniaxial strain, free
energy density
(6.10) reduces to the form
 | (6.19) |
The stress tensor at a uniaxial strain is
T = s11 e1
 e1 + s22(
e2
e1 + s22(
e2  e2 +
e3
e2 +
e3 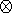 e3), and
the system of equilibrium equations is reduced to the single equation
e3), and
the system of equilibrium equations is reduced to the single equation
Hence, the normal stress
s11 in the solid phase is constant:
In the uniaxial strain case, the first formula in (6.11) relating the elastic
strain and temperature to the stress tensor yields
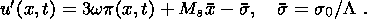 | (6.20) |
The evolutionary equation of plastic strain (6.13) in the uniaxial case has the
form
and its general solution is
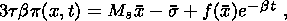 | (6.21) |
where
f(x) is an unknown function of the spatial coordinate
x to be determined.
In order to find
f(x), note that "instantaneous" (over a time
t  t )
melting of the part of the layer in the region
a(0)
t )
melting of the part of the layer in the region
a(0)  x
x 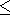 b takes place as
soon as the temperature at the boundary
x = b increases to the value
b takes place as
soon as the temperature at the boundary
x = b increases to the value
 =
=  1
>
1
>  0 at the time
t = 0, and the stress becomes equal to
s11 = - s0.
The
solid phase occupying the region
a(0)
0 at the time
t = 0, and the stress becomes equal to
s11 = - s0.
The
solid phase occupying the region
a(0) 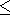 x
x  b at this time moment remains in
the elastic state because the viscous strain does not change over this time
interval. Further development of the process is controlled by the accumulation
of viscous strain and can be accompanied by an interface motion due to the
effect of the viscous strain on the stress state and energy of the solid phase.
Therefore, the function
f(x) is determined from the condition that the viscous
strain vanishes at
t = 0. Using (6.21), I find
b at this time moment remains in
the elastic state because the viscous strain does not change over this time
interval. Further development of the process is controlled by the accumulation
of viscous strain and can be accompanied by an interface motion due to the
effect of the viscous strain on the stress state and energy of the solid phase.
Therefore, the function
f(x) is determined from the condition that the viscous
strain vanishes at
t = 0. Using (6.21), I find
The expression for the plastic strain can then be written as
 | (6.22) |
Relation (6.22) specifies, in a comprehensive manner, the viscous strain field,
provided that the region occupied by the melt monotonically increases with time
due to the stress relaxation, i.e.
a (t)  a (0),
a (t)
a (0),
a (t)  0. Then, the solid phase
region
0
0. Then, the solid phase
region
0  x
x  a
(t) decreases with the time
t, and the solution is completely
determined by the initial data specified at
t = 0 in the interval
0
a
(t) decreases with the time
t, and the solution is completely
determined by the initial data specified at
t = 0 in the interval
0  x
x 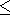 a
(0).
In this case, formulas (6.20) and (6.22) yield
a
(0).
In this case, formulas (6.20) and (6.22) yield
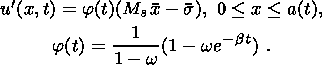 | (6.23) |
Hence, using the boundary condition
u(0, t) = 0, I obtain the expression for the
displacement
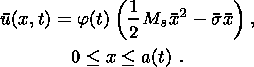 | (6.24) |
The unknown function
U(t) in (6.17) and the dimensionless coordinate of the phase
boundary
Z(t) = a(t)/b are determined by the coupling
conditions at the interface.
These are continuity conditions for the normal component of chemical potential
(3.23) and displacement (3.2):
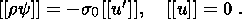 | (6.25) |
It is supposed here that the dissipation vanishes,
d = 0. The continuity
condition for the temperature and stress
s11 holds identically, and condition
(6.9) for inelastic deformations is not used because the new phase is an ideal
liquid.
= 0. The continuity
condition for the temperature and stress
s11 holds identically, and condition
(6.9) for inelastic deformations is not used because the new phase is an ideal
liquid.
Using (6.16), (6.18), (6.19), (6.23) and (6.24), coupling conditions (6.25) are
written in the form
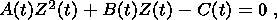 | (6.26) |
where
In what follows, I assume for simplicity that the differences of the bulk
modulus, thermal expansion coefficient and heat capacity in the solid phase
differ only slightly from the respective values in the liquid phase, i.e.
where
|d|  1 is a small
parameter characterizing the strain value of the
material. Let the rheological characteristics of the phase transition be
y = O(d2)
and
h = O (d2)
and let the initial stress in the
melt be
p = O(d). In this case, the following
estimates are valid accurate to the terms
O(d2):
1 is a small
parameter characterizing the strain value of the
material. Let the rheological characteristics of the phase transition be
y = O(d2)
and
h = O (d2)
and let the initial stress in the
melt be
p = O(d). In this case, the following
estimates are valid accurate to the terms
O(d2):
At the initial time moment
t = 0 the coefficients of system (6.26) are
Substituting the resulting expressions into (6.26) and taking into account
definitions (6.18) of the values
y and
h, the following equation is obtained:
 | (6.27) |
Hence, the melting onset corresponding to
Z0  Z(0) = 1 is controlled
by the
value
Mf = M0f ( s, w, y0,
h0, p) equal to the minimal
positive solution of equation (6.27) and
depends on characteristics of the phase transition
y0, h0
and
p, parameter
0
Z(0) = 1 is controlled
by the
value
Mf = M0f ( s, w, y0,
h0, p) equal to the minimal
positive solution of equation (6.27) and
depends on characteristics of the phase transition
y0, h0
and
p, parameter
0  w
w 1 - Ks/L
1 - Ks/L 1 and applied load
s.
1 and applied load
s.
|
|
Figure 1
|
If the temperature gradient is
M0f < Mf <  , a part of the layer melts. The
coordinate
0 < Z0 < 1 is determined by the expression
, a part of the layer melts. The
coordinate
0 < Z0 < 1 is determined by the expression
where
Y is, as before, the minimal positive solution of equation (6.27). The
dependence of the initial position of the interface on the stress
s applied to
the layer is shown in Figure 1 for the values
w = 0.1, 0.3, 0.6, 0.75 and 0.9
(respective curves 1-5). Figure 1a shows the dependence
Z0( s) for
p = 0.5 s ,
i.e. for the "normal" phase transition, with the density of the solid phase
exceeding the melt density. The value
s
,
i.e. for the "normal" phase transition, with the density of the solid phase
exceeding the melt density. The value
s is a characteristic stress such that
s
is a characteristic stress such that
s /L = O(d).
Figure 1b
shows similar curves, with the same values of
w, for
p = - 0.5 s
/L = O(d).
Figure 1b
shows similar curves, with the same values of
w, for
p = - 0.5 s ("anomalous" phase transition).
("anomalous" phase transition).
A characteristic feature of these curves is a monotonic variation
(a decrease or
increase in the respective cases of normal or anomalous transition) in the
initial thickness of the melt layer
1 - Z0 with increasing compressive
s at
small
w (curves 1 and 2 in Figure 1a). The behavior of curves 1 and 2
is consistent with traditional notions of the classical theory of phase
transitions: the applied pressure increases the temperature during the normal
phase transition and decreases it during the anomalous one. However, as
w increases,
the dependence of the initial melt thickness on the applied pressure
becomes nonmonotonic. The function
Z0( s) (curves 3-5) has
a maximum that
shifts, with increasing
w, toward smaller applied pressures for both normal
and
anomalous phase transitions. This feature is related to the effect of solid-state
properties on the phase transformation pattern noted in section 5. In the
vicinity of stress states, where
d Z0/d s
 , this can lead to instability of the
phase boundary and, in particular, to dynamic phenomena with slowly varying
boundary conditions.
, this can lead to instability of the
phase boundary and, in particular, to dynamic phenomena with slowly varying
boundary conditions.
Examination of the function
Z(t) at
t > 0 shows that the derivative
d Z(t)/dt is
positive at all of the considered values of the phase material parameters,
applied load and temperature gradient. This contradicts the initial assumption
on sign of the derivative
Z(t).
The problem considered excludes the case of a phase boundary retreating after a
part of the material had instantly melted ( Z(t) > Z(0) ). Actually, suppose
that
Z(t) > 0. Then the viscous strain of a solid phase particle forming
from the
melt at the interface vanishes. Using the first coupling condition in (6.25) at
the interface (the continuity of the normal component of the chemical potential
tensor) and taking into account formulas (6.16) and (6.18)-(6.20), it is readily
seen that this equation gives a constant value of the interface coordinate,
because the values in the relations considered are time independent.
Consequently, a retreating motion of the phase boundary is impossible in the
problem with boundary conditions considered. This means that the melt boundary
coordinate remains constant at
t > 0, and the surface
x = Z(0) is a contact
discontinuity. In accordance with (6.22) and (6.23), the total and viscous
strains change in solid phase material particles adjacent to this surface. Since
the viscous strain vanishes in a melt particle at the contact boundary, the
following relation holds:
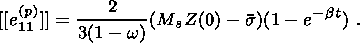 |
The evolution of the viscous strain at the contact discontinuity under
consideration leads at
t > 0 to a jump in the normal component of the chemical
potential:
In accordance with (6.26), the value of this jump can be written as
To sum up, the following features of phase transitions in solids associated with
the presence of stress relaxation are noteworthy.
An abrupt change in the boundary conditions that occurs over a time small
compared to the characteristic time of stress relaxation is accompanied by a
rapid movement of the phase boundary and complies with an instantaneous elastic
response of the material.
The evolution of plastic deformations at constant boundary conditions can either
increase or decrease the volume of the new phase, i.e. the interface can retreat
[Kondaurov and Nikitin, 1986].
The interface motion pattern depends on the
geometry of the region, boundary conditions and material parameters.
As the boundary conditions attain a stationary regime, the phase boundary can be
transformed into a contact discontinuity immobile relative to material
particles. Jumps in the tangential component of the displacement vector, viscous
strain and normal component of the chemical potential can arise at this
discontinuity surface.
Solid-state properties of the material can result in unstable behavior of the
phase boundary, including dynamic phenomena at slowly varying boundary
conditions.
References
Babichev, A. P., N. A. Babushkina, A. M. Bratkovskii, et al., A Handbook
of Physical Quantities (in Russian), Energoatomizdat, Moscow, 1991.
Bowen, R. M., Toward thermodynamics and mechanics of mixtures, Arch. Rat. Mech.
Anal., 24, (4), 370-403, 1967.
Bushman, A. V., I. V. Lomonosov, and V. E. Fortov, Equations of State
of Metals at High Energy Densities (in Russian), IKhFCh RAN, Chernogolovka, 1992.
Christian, J., Theory of Transformations in Metals and Alloys (in Russian),
vol. 1, Mir,
Moscow, 1978.
Coe, R. S., The thermodynamic effect of shear stress on the orthoclinoinversion
in enstatite and other coherent phase transition, characterized by finite simple
shear, Contribs. Mineral and Petrol., 26, 247, 1970.
Gibbs, J. W., The scientific papers, Thermodynamics, vol. 1, Longmans,
Green and
Co, New York, 1906.
Grinfeld, M. A., Methods of Continuum Mechanics in the Theory of Phase Transformations
(in Russian), Nauka, Moscow, 1990.
Khachaturyan, A. G., Theory of Phase Transformations and the Structure of Solid
Solutions (in Russian), Nauka, Moscow, 1974.
Knyazeva, A. G., Generalizations of the Clapeyron-Clausius equation in a self-consistent
thermomechanical model (in Russian), PMTF, 40, (6), 103-111, 1999.
Kondaurov, V. I., On conservation laws and symmetrization of nonlinear
thermoelastic equations (in Russian), DAN SSSR, 256, (4), 819-823, 1981.
Kondaurov, V. I., and L. V. Nikitin, Study of first-order phase transitions in
nonlinear elastic media (in Russian), Izv. AN SSSR, MTT, (6), 49-55, 1983.
Kondaurov, V. I., and L. V. Nikitin, First-order phase transitions in an elastic-
viscoplastic Medium (in Russian), Izv. AN SSSR, MTT, (4), 130-139, 1986.
Kondaurov, V. I., and L. V. Nikitin, Theoretical Foundations of Rheology of Geomaterials
(in Russian), Nauka, Moscow, 1990.
Kulikovskii, A. G., and E. I. Sveshnikova, Nonlinear Waves in Inelastic Media
(in Russian),
Nauka, Moscow, 1998.
Landau, L. D., and E. M. Lifshits, Statistical Physics (in Russian), Nauka,
Moscow, 1964.
Landau, L. D., and E. M. Lifshits, Hydrodynamics (in Russian), Nauka, Moscow,
1988.
Lee, E. H., Elastic-plastic deformation at finite strain, Trans. ASME. J. Appl.
Mech., 36, (1), 1-6, 1969.
Lurye, A. I., Nonlinear Theory of Elasticity (in Russian), Nauka, Moscow,
1980.
Mukhamediev, Sh. A., Fracture Processes in the Earth's Lithosphere (in Russian),
IFZ RAN,
Moscow, 1990.
Melosh, H. G., Impact Cratering: A Geological Process, Oxford Univ. Press,
New
York, 1989.
Ostapenko, G. T., Thermodynamics of Nonhydrostatic Systems and its Applications
in the Theory of Metamorphism (in Russian), Naukova dumka, Kiev, 1977.
Ovsyannikov, L. V., Lectures on Fundamentals of Gas Dynamics (in Russian),
Nauka, Moscow, 1981.
Robin, P. Y. F., Thermodynamic equilibrium across a coherent interface in a
stressed crystal, Amer. Miner., 59, (11-12), 1286, 1974.
Roitburd, A. L., Theory of the heterogeneous structure formation due to phase
transformations in solids (in Russian), UFN, 113, (1), 69-104, 1974.
Rozhdestvenskii, B. L., and N. N. Yanenko, Systems of Quasi-Linear Equations
and Their Applications in Gas Dynamics (in Russian), Nauka, Moscow, 1978.
Sadovskii, V. M., Discontinuous Solutions in Dynamic Problems of Elastic-Plastic
Media (in Russian), Nauka, Moscow, 1997.
Sedov, L. I., Continuum Mechanics (in Russian), vols. 1 and 2, Nauka,
Moscow, 1970.
Truesdell, C., A First Course in Rational Continuum Mechanics, Johns Hopkins
Univ., Baltimore, Maryland, 1972.
Truskinovskii, L. M., On the chemical potential tensor (in Russian), Geokhimiya,
(12),
1730-1744, 1983.
Turcott, D. L. and G. Schubert, Geodynamics: Applications of Continuum Physics
to Geological Problems, John Wiley, New York, 1982.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on May 3, 2002.
 q
q q0/l0 and
an Euler number
r0v20/s0
q0/l0 and
an Euler number
r0v20/s0 1,
where
q0, l0, r0,
v0 and
s0 are the characteristic temperature,
linear size of the body, density, velocity and pressure, respectively. It is additionally
assumed that the velocity of the interface is small compared to the velocity of sound,
and no
singular sources of mass, momentum, energy and entropy are present on the
interface.
1,
where
q0, l0, r0,
v0 and
s0 are the characteristic temperature,
linear size of the body, density, velocity and pressure, respectively. It is additionally
assumed that the velocity of the interface is small compared to the velocity of sound,
and no
singular sources of mass, momentum, energy and entropy are present on the
interface.
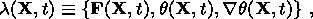
 c(t)
of the reference configuration
of the body
k into the current configuration
c(t). The nonsymmetric
second-rank tensor F connects the radius-vectors differentials of two
neighboring material points:
c(t)
of the reference configuration
of the body
k into the current configuration
c(t). The nonsymmetric
second-rank tensor F connects the radius-vectors differentials of two
neighboring material points:
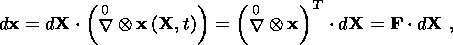
 k.
The following polar decomposition holds for the nonsingular tensor F:
k.
The following polar decomposition holds for the nonsingular tensor F:
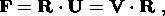
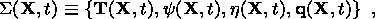

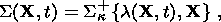
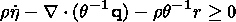
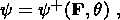
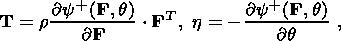
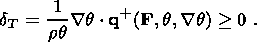
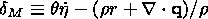
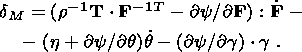
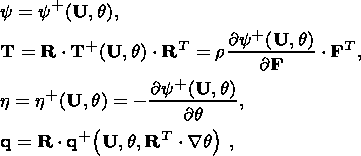

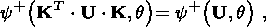
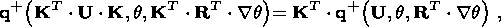
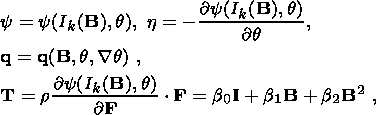
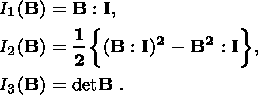
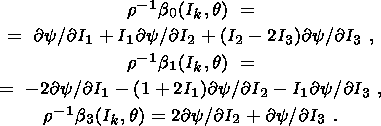
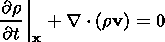
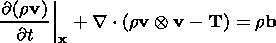
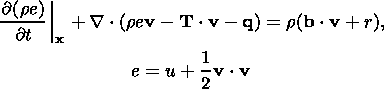
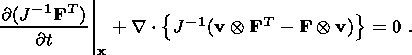
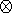 means the tensor product,
u is the
internal energy density,
e = u + 1/2 v
means the tensor product,
u is the
internal energy density,
e = u + 1/2 v 
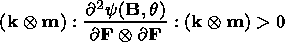
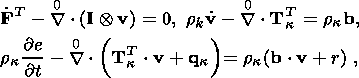

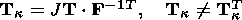
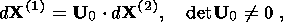
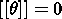
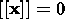
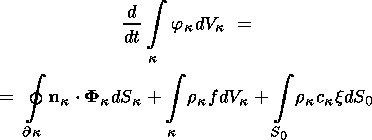
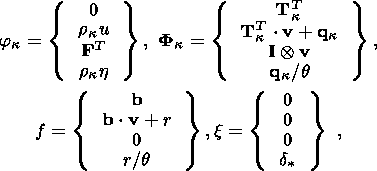
 ,
the
case
d
,
the
case
d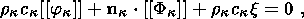
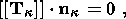
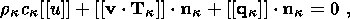
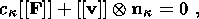
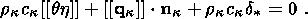
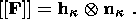
 X/
X/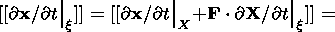

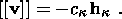
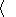 a
a 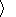 [[b]] + [[a]]
[[b]] + [[a]] 
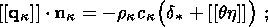
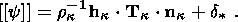
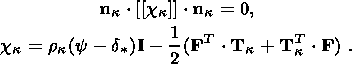
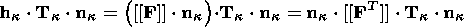
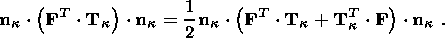
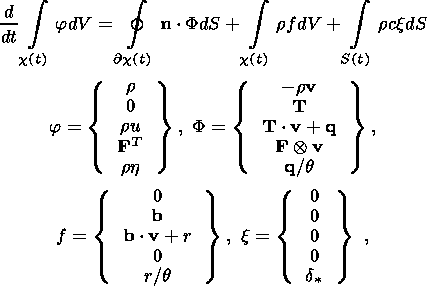
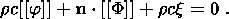
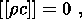
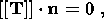
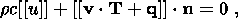
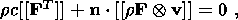
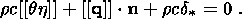
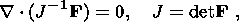
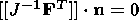
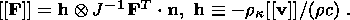
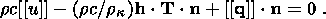
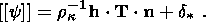
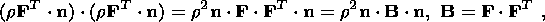
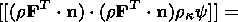
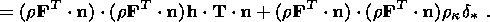
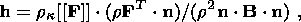
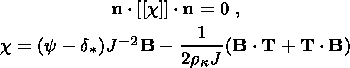

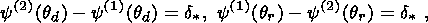
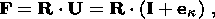
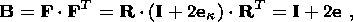
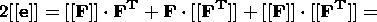
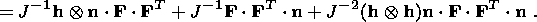
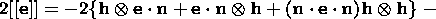
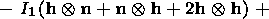
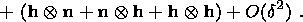
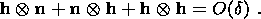
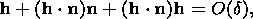
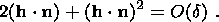
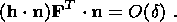
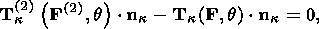
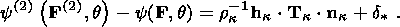
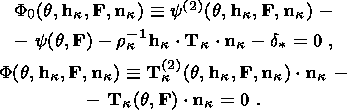
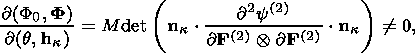
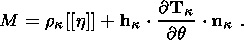
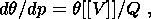
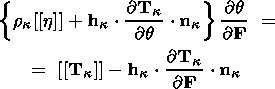
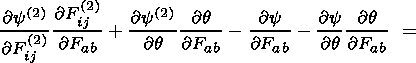
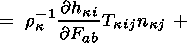
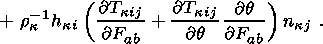
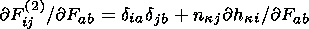
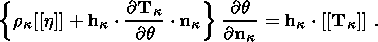
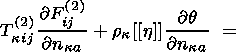
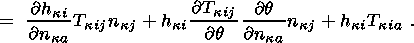
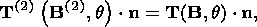
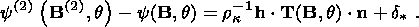
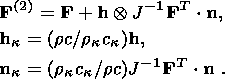
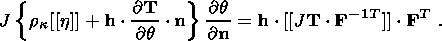
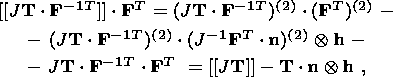
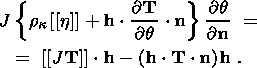
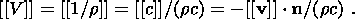
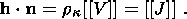
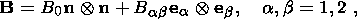
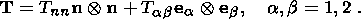
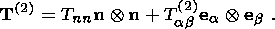
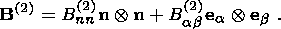
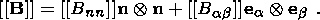
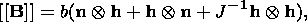
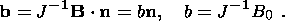
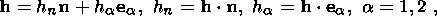
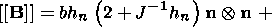
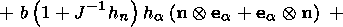
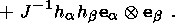
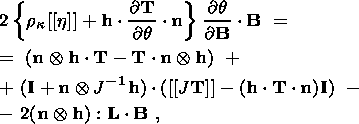
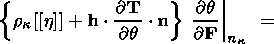
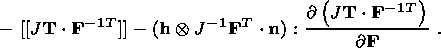
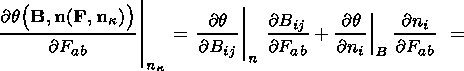
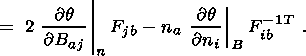
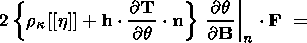
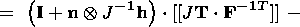
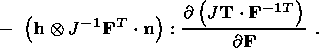
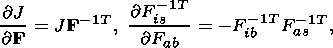
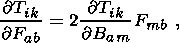
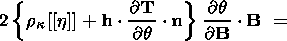
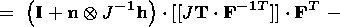
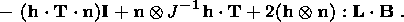
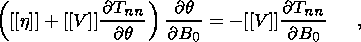
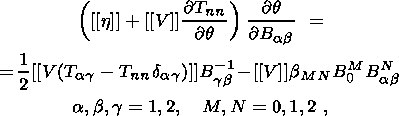
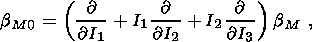
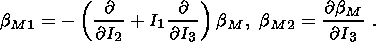
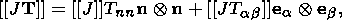
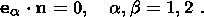
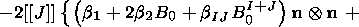
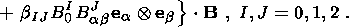
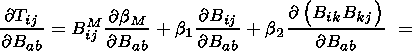
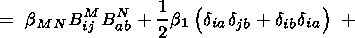
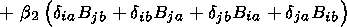
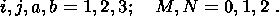
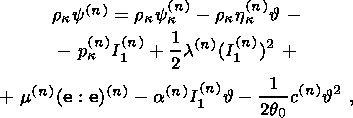
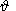 = q - q0,
= q - q0,
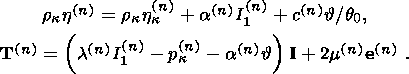
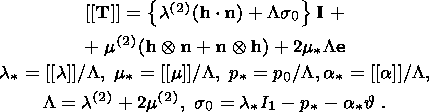
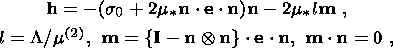
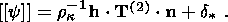
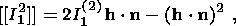
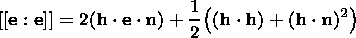
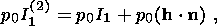
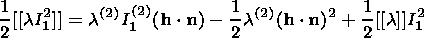
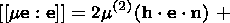
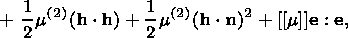
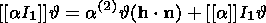
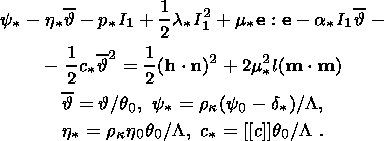
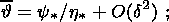
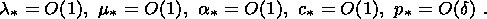
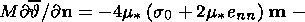
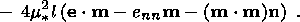
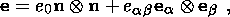
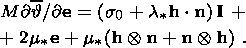
 :
e
:
e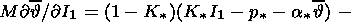
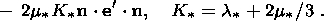
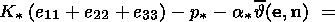
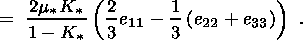
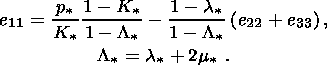
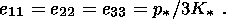
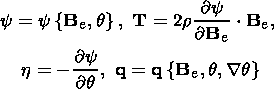
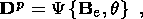
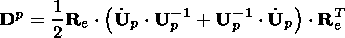
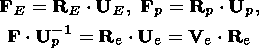
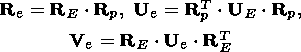
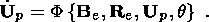
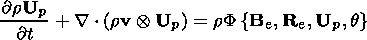
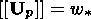
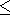 x
x 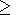 0. A constant
normal compressive stress
- s0,
s>0, is applied to the boundary
x = b at the time
t = 0, and the temperature of the medium increases to a value
q1 = const>0 at which a part of the
layer adjacent to the boundary
x = b melts.
The boundary of the melting region is found from the solution of the problem.
Mass forces and distributed heat sources are neglected.
0. A constant
normal compressive stress
- s0,
s>0, is applied to the boundary
x = b at the time
t = 0, and the temperature of the medium increases to a value
q1 = const>0 at which a part of the
layer adjacent to the boundary
x = b melts.
The boundary of the melting region is found from the solution of the problem.
Mass forces and distributed heat sources are neglected.
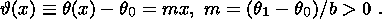
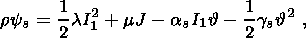
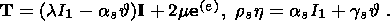
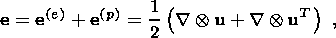
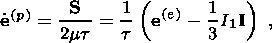
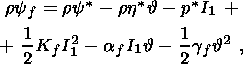
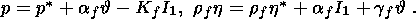
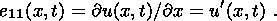
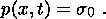
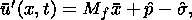
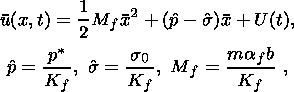
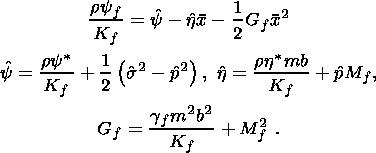
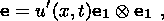
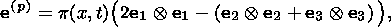
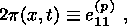
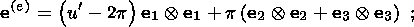
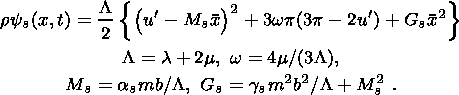
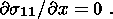
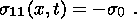
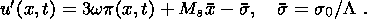
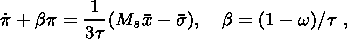
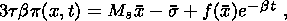

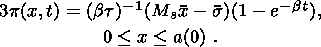
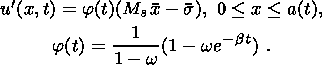
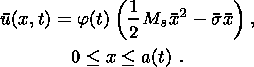
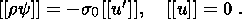
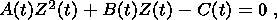
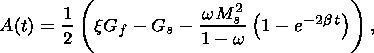
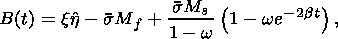
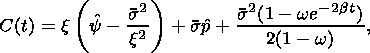
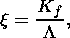
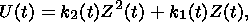
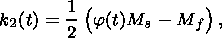
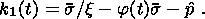
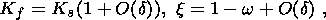
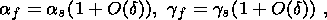
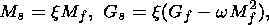
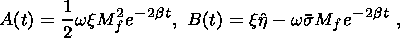
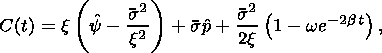
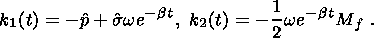
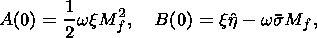
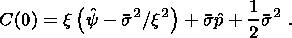
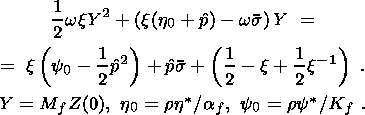

 , a part of the layer melts. The
coordinate
0 < Z0 < 1 is determined by the expression
, a part of the layer melts. The
coordinate
0 < Z0 < 1 is determined by the expression