Russian Journal of Earth Sciences
Vol. 4, No. 1, February 2002
Global stresses in the Western Europe lithosphere
and the collision forces in the Africa-Eurasia convergence zone
Sh. A. Mukhamediev
Schmidt United Institute of Physics of the Earth, Russian Academy
of Sciences
Contents
Abstract
The experimentally determined directions of the maximum
horizontal compressive
stress
SH, max in the western European stress province
(WESP) of the West European
platform are mostly oriented northwest with an average azimuth of 325o
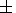 26o. The
traditional approach to the mathematical modeling of the stress field in the
Western Europe lithosphere (as well as in other stable lithospheric blocks) is
based on an elastic model of the medium and boundary conditions that specify
stresses and/or displacements at the entire perimeter of the region studied. In
the particular case of Western Europe, poorly constrained boundary conditions
should be set at the southern (in the collision zone of the African and Eurasian
plates) and eastern boundaries of the region. For this purpose, experimental
directions of
SH, max are used as constraints on the sought-for
solution. However,
even if the experimental directions of
SH, max agree well with their theoretical
estimates, model stress magnitudes are still sensitive to the choice of model
boundary conditions.A basically different approach proposed and implemented in this
work for determining the field of tectonic stresses uses the
experimental directions of
SH, max as input
information rather than constraints on the sought-for solution.
The spatially persisting strike of the
SH, max axis
makes it possible to construct the field of straight trajectories
of principal stresses on the WESP territory. The problem of stress
determination is then reduced to the hyperbolic-type problem of
integrating the equilibrium equations that does not require
postulating constitutive relations, and the boundary conditions
are only specified on some part of the boundary of the model
region. The lithosphere material can be mechanically anisotropic
and inhomogeneous. Stresses
tR produced by the
ridge push were specified in this work on a segment of the
Mid-Atlantic Ridge, and stresses
tC due to the
Africa-Europe collision were specified in the convergence zone. No
boundary conditions are required at the eastern boundary of the
region studied. Supposedly, straight trajectories of stresses can
be extended into oceanic lithosphere areas adjacent to the
continent. The formulation of the problem presented in the paper
provides substantial constraints on the collision stresses
tC. These constraints directly result from the equilibrium conditions
of the Western Europe lithosphere rather than from the plate
convergence kinematics in the collision zone. A simple analytical
expression obtained for the tensor of global tectonic stresses in
the study region indicates that the
SH, max magnitude
decreases in the NW direction. The minimum horizontal stress in
the WESP region is shown to be sensitive to the direction of the
collision stresses
tC. This stress whose modulus
increases in the SE direction is compressive, zero or tensile
depending on whether the vector of collision stresses
tC deviates westward from the
SH, max direction, coincide with it or deviates eastward
from it. The
modification of the inferred solution incorporating stresses
applied at the base of the lithospheric plate is discussed.
26o. The
traditional approach to the mathematical modeling of the stress field in the
Western Europe lithosphere (as well as in other stable lithospheric blocks) is
based on an elastic model of the medium and boundary conditions that specify
stresses and/or displacements at the entire perimeter of the region studied. In
the particular case of Western Europe, poorly constrained boundary conditions
should be set at the southern (in the collision zone of the African and Eurasian
plates) and eastern boundaries of the region. For this purpose, experimental
directions of
SH, max are used as constraints on the sought-for
solution. However,
even if the experimental directions of
SH, max agree well with their theoretical
estimates, model stress magnitudes are still sensitive to the choice of model
boundary conditions.A basically different approach proposed and implemented in this
work for determining the field of tectonic stresses uses the
experimental directions of
SH, max as input
information rather than constraints on the sought-for solution.
The spatially persisting strike of the
SH, max axis
makes it possible to construct the field of straight trajectories
of principal stresses on the WESP territory. The problem of stress
determination is then reduced to the hyperbolic-type problem of
integrating the equilibrium equations that does not require
postulating constitutive relations, and the boundary conditions
are only specified on some part of the boundary of the model
region. The lithosphere material can be mechanically anisotropic
and inhomogeneous. Stresses
tR produced by the
ridge push were specified in this work on a segment of the
Mid-Atlantic Ridge, and stresses
tC due to the
Africa-Europe collision were specified in the convergence zone. No
boundary conditions are required at the eastern boundary of the
region studied. Supposedly, straight trajectories of stresses can
be extended into oceanic lithosphere areas adjacent to the
continent. The formulation of the problem presented in the paper
provides substantial constraints on the collision stresses
tC. These constraints directly result from the equilibrium conditions
of the Western Europe lithosphere rather than from the plate
convergence kinematics in the collision zone. A simple analytical
expression obtained for the tensor of global tectonic stresses in
the study region indicates that the
SH, max magnitude
decreases in the NW direction. The minimum horizontal stress in
the WESP region is shown to be sensitive to the direction of the
collision stresses
tC. This stress whose modulus
increases in the SE direction is compressive, zero or tensile
depending on whether the vector of collision stresses
tC deviates westward from the
SH, max direction, coincide with it or deviates eastward
from it. The
modification of the inferred solution incorporating stresses
applied at the base of the lithospheric plate is discussed.
Introduction
A large amount of experimental data on in situ stresses has been gathered
over
a nearly half-century period of studying the stress state of the Western Europe
lithosphere. The experimental data on the present tectonic stresses were
obtained from both instrumental measurements and the analysis of seismological
observations. Even the early measurements of stresses made in the 1960s and
early 1970s (e.g. see
[Ahorner, 1975;
Greiner, 1975])
revealed a uniform NW orientation of the axis of the maximum horizontal compressive
stress
SH, max and provided some constraints on the tectonics
and seismicity of large geological
structures such as the Rhine system of grabens
[Ahorner, 1975;
Illies and Greiner, 1979; and others].
Later, new constraints on stresses were gained and
the existing data were generalized as a result of investigations within the
framework of the World Stress Map (WSM) Project
[Grünthal and Stromeyer, 1992;
Müller et al., 1992;
Zoback, 1992;
Zoback et al., 1989].
In particular, these studies confirmed that the
SH, max axis distribution is homogeneous
over large areas in Western Europe, demonstrated that the
SH, max direction is virtually
independent of depth and determined the variation of the
SH, max orientation pattern
in the direction toward the East European platform. Large geological structures in
Western Europe such as the Alps were shown to disturb the homogeneity of the
global stress orientation on regional and local scales. (note 1)
Later studies were focused on the verification and improvement of stress data
and on gaining new results for Western Europe regions and structures. New
measurements of present stresses were made in Northern Europe (Barents and North
seas)
[Gölke and Brudy, 1996;
Wirput and Zoback, 2000],
on the Iberian Peninsula (where paleostresses were also analyzed)
[Andeweg et al., 1999;
De Vicente et al., 1996],
in British Isles
[Becker and Davenport, 2001],
in the Apennines
[Frepoli and Amato, 2000;
Montone et al., 1999],
and in France, Germany and Austria
[Cornet and Yin, 1995;
Delouis et al., 1993;
Plenefisch and Bonjer, 1997;
Reinecker and Lenhardt, 1999;
Scotti and Cornet, 1994;
Yin and Cornet, 1994].
Tectonic stresses of second order were studied and their
geodynamic interpretations were proposed for the Alps
[Delouis et al., 1993;
Eva and Solarino, 1998;
Eva et al., 1998;
Regenauer-Lieb, 1996],
Apennines
[Boncio and Lavecchia, 2000;
Collettini et al., 2000],
and Rhinegraben
[Delouis et al., 1993;
Plenefisch and Bonjer, 1997].
It is assumed that the global stress field in Western Europe is mainly
controlled by the push from the central and northern segments of the Mid-Atlantic
Ridge (MAR) and by the collision forces arising due to convergence of
Africa and Europe
[Grünthal and Stromeyer, 1992;
Müller et al., 1992].
As distinct from the push force, both the modulus and direction of collision
forces have been poorly studied
[Albarello et al., 1995;
Gölke and Coblenz, 1996;
Richardson, 1992].
Also ambiguous are geological-geophysical kinematic models
[Albarello et al., 1995;
Argus et al., 1989;
Savostin et al., 1986]
and satellite geodesy data on movements and deformations in the collision zone
[Campbell and Nothnagel, 2000;
Noomen et al., 1996].
In this context, results of numerical modeling of the stress field in Western
Europe based on the traditional approach that requires the specification of
boundary conditions on the entire boundary of the study region (e.g. see
[Gölke and Coblenz, 1996])
are very sensitive to the assumptions on the characteristics
of collision forces and on the poorly constrained stresses (or displacements) at
the eastern boundary. The coincidence of theoretical and experimental directions
of
SH, max at the stress measurement points within
the study area by no means remove
the ambiguity of resulting solutions
[Mukhamediev, 2000;
Mukhamediev and Galybin, 2001].
The approach applied in this work to the mathematical modeling of the tectonic
stress field was proposed in
[Mukhamediev, 1991].
The problem is reduced to the
construction of the field of principal stress trajectories and the subsequent
integration of equilibrium equations, with boundary conditions specified only on
part of the Western Europe boundary. In principle, this approach allows one to
impose significant constraints on the distribution pattern of forces arising due
to the Africa-Europe convergence.
1. Experimental Data on the Tectonic Stresses in the
Western Europe
Lithosphere and Convergence Kinematics of Africa and Eurasia
1.1. Methods of Stress Measurements
The following methods were used for local instrumental measurements of stresses
in Western Europe:
- various overcoring methods applied to unload samples taken during drilling
operations in mines, tunnels and quarries
[Becker and Davenport, 2001;
Greiner, 1975;
Greiner and Illies, 1977;
Illies and Greiner, 1979; and others];
- jacking methods according to which a plane or circular slot is cut in a rock
mass, and a loading device (jack) inserted into the slot raises pressure until
the strain developed during the creation of the slot vanishes
[Froidevaux et al., 1980];
- borehole slotting methods for measuring the strain release near slots cut in borehole
walls
[Amadei and Stephanson, 1997;
Becker, 1999];
- methods of hydraulic fracturing which determine both the direction of extreme
horizontal stresses and the minor principal stress magnitude
[Amadei and Stephanson, 1997;
Zoback et al., 1993];
- borehole caliper measurements for detecting ellipticity caused by borehole breakouts
[Gölke and Brudy, 1996;
Wirput and Zoback, 2000;
Zoback et al., 1989].
Methods of reconstructing the present stress state of the Western Europe
lithosphere from seismological data have recently become widespread
[De Vicente et al., 1996;
Frepoli and Amato, 2000;
Eva and Solarino, 1998;
Eva et al., 1998;
Montone et al., 1999;
Plenefisch and Bonjer, 1997;
Scotti and Cornet, 1994].
Some authors associate the directions of extreme stresses with the axes
P and
T of focal mechanisms (e.g. see
[Ahorner, 1975;
Montone et al., 1999]).
Presently, the principal axis orientations of the stress tensor
T are mostly
determined from a certain set of focal mechanisms of earthquakes using methods
developed in
[Gephart and Forthsyth, 1984;
Rivera and Cisternas, 1990; and
others].
These methods are based on the assumption that the slip direction and
the direction of the maximum resolved shear stress coincide on the fault slip
planes and, in the opinion of their authors, allow the reconstruction of the
principal axis directions and the parameter
R characterizing the relative
differences of principal stresses. (note 2)
Theoretical substantiation of some of the aforementioned methods is based on
several restrictive assumptions on rock properties and the stress distribution
patterns in rock masses where stresses were measured. The presence of large
stress gradients, local heterogeneities in samples and rocks masses, departures
of rocks from linear-elastic behavior and other factors can be sources of
significant errors in interpretation of the measurements
[Grob et al., 1975;
Harper and Szymanski, 1991;
Ranalli, 1975;
Rutqvist et al., 2000].
Some authors combine various methods in order to more reliably determine local stress
state
elements. Thus, an algorithm of joint inversion of seismological and hydraulic
fracturing data was applied to the stress determination in central France
[Cornet and Yin, 1995;
Yin and Cornet, 1994],
and constraints on the stress state in the overdeep KTB borehole area (southern Germany)
were gained from both hydraulic fracturing results and caliper measurements
[Zoback et al., 1993].
Various methods differ in the amount of information on stress state elements
that they can provide. The overcoring methods alone can, in principle, provide
constraints on all components of the local stress tensor
T. Other methods can
be helpful for determining the principal axis orientations of the tensor
T and,
perhaps, for gaining additional constraints on the local stress state. However,
the overcoring methods are affective only at small depths because, similar to
the jacking methods, they are applied near the Earth's surface. The hydraulic
fracturing methods and borehole caliper measurements are sources of data on
stresses at depths of up to a few kilometers and fill the gap between near-surface
indicators on the one hand and seismological data on the other
[Amadei and Stephanson, 1997].
Focal mechanisms of earthquakes are actually the only
source of information about stresses in Western Europe at depths greater than 5 km
[Müller et al., 1992].
Experimental measurements usually indicate that two of the three principal axes
of the stress tensor
T are subhorizontal
[Müller et al., 1997;
Zoback, 1992;
Zoback et al., 1989; and others]. (note 3)
This observation makes
it possible to introduce the notion of the stress regime. The stress regimes can
be classified as those of compression ( SH, max>SH, min>S
V ),
shear ( SH, max>SV>SH, min )
and
extension ( SV>SH, max>SH, min )
[Zoback et al., 1989].
Henceforward, compressive stresses are positive;
SH, max and
SH, min are, respectively, maximum and minimum
normal horizontal stresses; and
SV is the principal vertical stress due to the
weight of rocks. After to
Anderson [1951],
the aforementioned regimes are often interpreted in terms of faulting deformations
and are referred to as, respectively, regimes of thrust or reverse faulting,
strike-slip faulting and normal faulting
[Amadei and Stephanson, 1997;
Zoback et al., 1989].
In addition to the present-day in situ stresses, paleostresses were determined
in various regions of Western Europe. These determinations are based on such
methods as the analysis of tectonic stilolites
[Illies, 1975;
Letouzev, 1986],
inversion of striation data from variously oriented planes of joints in rocks
[Letouzev, 1986]
and faulting data from variously oriented faults
[De Vicente et al., 1996],
and examination of the attitude, strike and deformation of geological bodies
[Andeweg et al., 1999].
The difficulties of dating the activity periods of paleostresses were in part
compensated for by the fact that their kinematic indicators were studied in
relatively young rocks (usually not older than the Late Cretaceous).
1.2. Stress Orientations and Deformation Regimes in the
Western Europe
Lithosphere
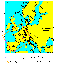
|
|
Figure 1
|
Experimental data indicate that, similar to some other regions
of the Earth, the
Western Europe lithosphere is commonly subjected to the action of the stress
SH, max uniformly oriented northwest and north-northwest
(Figure 1).
These results
obtained in the 1960s and early 1970s (e.g. see
[Ahorner, 1975;
Greiner, 1975])
were generalized within the framework of the WSM Project
[Grünthal and Stromeyer, 1992;
Müller et al., 1992;
Zoback, 1992;
Zoback et al., 1989; and others].
The NW orientation of
SH, max cease to be predominant east of
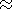 14o E
[Grünthal and Stromeyer, 1992;
Müller et al., 1992].
The
SH, max direction is virtually independent of depth
and is not affected by short-wavelength
variations in the thickness of the lithosphere, its structural features and topography
[Müller et al., 1992;
Richardson, 1992].
Large geological structures (e.g. the Alps) superimpose
regional signatures on the global orientation of the stresses
[Müller et al., 1992].
14o E
[Grünthal and Stromeyer, 1992;
Müller et al., 1992].
The
SH, max direction is virtually independent of depth
and is not affected by short-wavelength
variations in the thickness of the lithosphere, its structural features and topography
[Müller et al., 1992;
Richardson, 1992].
Large geological structures (e.g. the Alps) superimpose
regional signatures on the global orientation of the stresses
[Müller et al., 1992].
Figure 1 shows generalized directions of
SH, max inferred in
[Balling and Bauda, 1992;
Müller et al., 1992].
The data generalization allows one to exclude from the
analysis local disturbances in the stress orientation and to analyze the
averaged regional field of the
SH, max directions as a function of driving forces
applied at plate boundaries. Three large provinces of stresses have been
distinguished in the spatial distribution of the
SH, max orientation in Western Europe
[Müller et al., 1992,
1997]:
(1) western European stress province (WESP) north of the Alps and Pyrenees,
with
the
SH, max axis consistently striking 325o
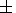 26o
[Ahorner, 1975;
Grünthal and Stromeyer, 1992;
Illies and Greiner, 1979;
Müller et al., 1992,
1997;
Zoback, 1992;
Zoback et al., 1989];
26o
[Ahorner, 1975;
Grünthal and Stromeyer, 1992;
Illies and Greiner, 1979;
Müller et al., 1992,
1997;
Zoback, 1992;
Zoback et al., 1989];
(2) northern European stress province north of
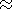 55o N including Fennoscandia and
characterized by a wide scatter in the azimuths of the
SH, max axis strike (300o
55o N including Fennoscandia and
characterized by a wide scatter in the azimuths of the
SH, max axis strike (300o
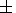 45o)
[Gölke and Brudy, 1996;
Müller et al., 1992;
Wirput and Zoback, 2000; and others];
45o)
[Gölke and Brudy, 1996;
Müller et al., 1992;
Wirput and Zoback, 2000; and others];
(3) Aegean-Anatolian stress province approximately defined by the coordinates
(27o-37o E, 34o-42o N) and characterized
by an E-W orientation of the
SH, max axis
(265o
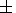 27o), with the normal and strike-slip
faulting regimes prevailing west and
east of
27o), with the normal and strike-slip
faulting regimes prevailing west and
east of
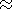 30o E, respectively
[Gölke and Coblenz, 1996;
Müller et al., 1992,
1997;
Zoback et al., 1989].
30o E, respectively
[Gölke and Coblenz, 1996;
Müller et al., 1992,
1997;
Zoback et al., 1989].

|
|
Figure 2
|
The aforementioned generalized properties of the stress field in various regions
and large geological structures of Western Europe were confirmed and, in some
cases, significantly revised by later investigations. In the context of this
work, most interesting is the WESP region distinguished by the most uniform
distribution of principal stresses. The WESP territory is dominated by the
strike-slip faulting regime with nearly vertical orientation of the intermediate
principal stress, although WESP also includes regions dominated
by extension and
compression regimes
[Müller et al., 1992,
1997].
The boundaries between the large provinces of stresses mentioned above can be
delineated only tentatively; therefore, the WESP territory adopted here (the
rectangle
BB D
D D in Figures 1 and 2) is somewhat larger than the territory considered in
[Müller et al., 1992,
1997].
I discuss in more detail the spatial distribution of the stress state
characteristics in WESP and adjacent regions.
D in Figures 1 and 2) is somewhat larger than the territory considered in
[Müller et al., 1992,
1997].
I discuss in more detail the spatial distribution of the stress state
characteristics in WESP and adjacent regions.
The uniform NW orientation of the maximum horizontal compressive stress of first
order is well expressed on the most territory of France, as is indicated by
instrumental and seismological observations
[Cornet and Yin, 1995;
Delouis et al., 1993;
Froidevaux et al., 1980;
Scotti and Cornet, 1994;
Yin and Cornet, 1994].
The same orientation is typical of British Isles (e.g. see
[Becker and Davenport, 2001]).
The NW orientation of the
SH, max axis in Germany and Belgium is
supported by both instrumental measurements
[Greiner, 1975]
and seismicity pattern in linear weakened zones; focal mechanisms indicate the strike-slip
faulting regime in such of these zones that strike in the NNE and WNW directions
(the Upper Rhinegraben, Belgian zone, and others), i.e. roughly along the
direction of the maximum horizontal shear stress
tmax, whereas the
extension regime characterizes, for example, the Lower Rhinegraben striking NW
(i.e. along the
SH, max direction), as is evident from normal motions
on fault
planes parallel to the graben strike
[Ahorner, 1975;
Delouis et al., 1993;
Illies and Greiner, 1979;
Plenefisch and Bonjer, 1997].
Reliable fault plane solutions for earthquakes in the western Pyrenees also indicate
the NNW and NW orientations of the
SH, max axis
[Delouis et al., 1993].
The convergence of Africa and Europe gave rise to the formation of sedimentary basins
in central Spain,
which advantageous for the reconstruction of the neotectonic paleostress evolution
[Andeweg et al., 1999;
De Vicente et al., 1996].
Paleostress studies and the analysis of focal mechanisms showed that, from the Middle
Miocene to the present time,
SH, max axis azimuths have remained within a 310o-340o
interval
[De Vicente et al., 1996].
The present pattern of stress orientations is most distorted in seismically
active regions of the Apennines and Alps. Strong variations in stress
orientations over comparatively small distances superimposed on the global field
in the Apennines are due to the underthrusting of the Adriatic microplate
beneath the southern Alps and other complex geodynamic processes developing in
the immediate vicinity of this region
[Frepoli and Amato, 2000;
Montone et al., 1999].
However, the extension regime prevailing over the most territory of
northern and central Italy, the orientations of principal stress axes retain the
same properties as in the WESP province, namely: the
SH, min axis has the NE
orientation (orthogonal to the Apennines strike)
[Frepoli and Amato, 2000;
Montone et al., 1999].
Tensile deformations result in thinning of the crust (20-25 km) and higher heat
flow values
[Collettini et al., 2000].
Structural features associated with the NE orientation of the
SH, min axis are large, NW-NNW striking
active normal faults accounting for the main seismicity and Pliocene-Quaternary
sedimentary basins elongated in the same direction
[Boncio and Lavecchia, 2000;
Collettini et al., 2000].
The compression regime with the NE striking
SH, max axis exists only in a small
area in the east of northern Apennines (near the Adriatic coast)
[Collettini et al., 2000;
Frepoli and Amato, 2000;
Montone et al., 1999].
The compression axes in the Alps, as constrained by focal mechanisms of
earthquakes, are on a first approximation close to the directions of horizontal
shortening of the crust reconstructed from the kinematic analysis of neotectonic
structures
[Balling and Bauda, 1992;
Müller et al., 1992].
The maximum horizontal stress axis trends nearly N-S in the Swiss Alps, as is
also established from data of instrumental measurements
[Becker, 1999].
The properties of the stress field mentioned above are evidence that the deformation
pattern in this region has not changed over a few last millions of years. Later
and more detailed studies of seismicity discovered an inhomogeneous fine
structure of the stress axes distribution
[Eva and Solarino, 1998;
Eva et al., 1998].
Thus, the observed spatial variations in the stress regime yield evidence
of a near-surface extension regime superimposed on the regional compression
regime. This effect is accounted for by gravitational spreading at ridge crests
[Eva and Solarino, 1998].
Significant lateral inhomogeneity of the stress field in
the southwestern Alps is related to an arcuate geometry of the ridges
[Delouis et al., 1993].
Other interpretations of the stress field pattern in the Alps in
terms of regional geodynamic models are also known. Thus,
Regenauer-Lieb [1996]
interprets the stress-strain state in the region within the framework of a model
in which a relatively rigid "Italian-Adriatic die" is indented in the NW
direction into the Western Europe lithosphere.
The overview of experimental data on the stress orientations suggests a nearly
uniform global NW orientation of the
SH, max axis in the Western Europe lithosphere.
Regional disturbances in the field of trajectories mainly arise as a response of
structural and mechanical inhomogeneities of the lithosphere to the
aforementioned global compression direction. The majority of researchers
associate the global NW orientation of the compression axis with driving forces:
the push produced by MAR and the collision force due to the convergence of
Africa and Europe. However, there is no agreement with regard to the relative
contributions of these forces. It is generally supposed that the both forces are
equally responsible for the observed features of the global stress field (e.g. see
[Ahorner, 1975;
Grünthal and Stromeyer, 1992;
Müller et al., 1992,
1997]).
However, some authors believe that the WESP stress field can be accounted for by
the push alone, without invoking the collision forces
[Gölke and Coblenz, 1996;
Richardson, 1992],
whereas others apply only the collision forces
[Letouzev, 1986].
1.3. Kinematics of the Africa-Europe Convergence
The kinematics of the Africa-Europe convergence was analyzed by reconstructing
the motions of these plates relative to North America from magnetic lineations
in northern and central Atlantic, transform fault strikes and other geological
and geophysical evidence (e.g. see
[Argus et al., 1989;
DeMets et al., 1990;
Savostin et al., 1986]).
The paleoreconstructions showed that, in the central Mediterranean, Africa and
Eurasia converged in the NW-SE or N-S directions over the last 9-10 Myr
[Savostin et al., 1986].
The geological-geophysical reconstruction of recent movements of lithospheric plates
is
consistent with such a direction of convergence. The convergence occurs at a rate
of 4-7 mm/yr
and is accompanied by a counterclockwise rotation of Africa relative to Eurasia
around a (21o N, 21o W) pole
[Argus et al., 1989;
DeMets et al., 1990;
Gripp and Gordon, 1990].
However, these results cannot be acknowledged being unambiguous
because they are based on some restrictive assumptions. In particular, plate
deformations in the collision zone are neglected (whereas Africa and Eurasia
converge within a fairly wide zone of active deformations), and the entire
Eurasian plate is supposed to move as a rigid block. Removal of some of these
assumptions can dramatically change the results of kinematic reconstructions.
Thus, if the western end of Eurasia (the so-called Iberian block) is let to move
independently of the rest of the Eurasian plate, the analysis of kinematic
indicators in North Atlantic admits alternative solutions, namely: an NNE-SSW or
NE-SW direction of the Africa-Eurasia convergence is consistent with kinematic
evidence within experimental uncertainties
[Albarello et al., 1995].
Direct measurement of velocities in the collision zone of the African and
Eurasian plates is presently based on satellite geodesy data. Very long-base
interferometry (VLBI) methods
[Campbell and Nothnagel, 2000],
GPS measurements and satellite laser ranging (SLR)
[Kahle et al., 1998;
Noomen et al., 1996]
are used. Unfortunately, GPS stations and SLR measurements are few in the western
and central Mediterranean regions, which are of interest here, and the results
of velocity measurements are much less liable to interpretation than, for
example, similar measurements in the eastern Mediterranean
[Kahle et al., 1998;
Noomen et al., 1996].
The velocity vectors supporting the geological-geophysical NUVEL-1 model of plate
motion
[DeMets et al., 1990;
Gripp and Gordon, 1990]
are obtained only at two stations in North Africa and at one station in southern
Italy. Results inconsistent with NUVEL-1 are interpreted in terms of either
their statistical insignificance or local deformation processes
[Noomen et al., 1996].
VLBI measurements of velocity with the use of radio telescopes are also
too few for their reliable interpretation. Three sites in Italy are established
to move approximately in northward and northeastward directions at a rate of 3-5 mm/yr,
which is treated as a response to the subduction of the African plate,
whereas measurements at one site in Spain are treated as evidence for virtual
immobility of the Iberian Peninsula relative to central Europe (as distinct from
movements in the geological past)
[Campbell and Nothnagel, 2000].
Velocity vectors obtained from GPS and SLR measurements poorly agree with VLBI constraints.
Note that, even if the Africa-Europe convergence kinematics is reliably
reconstructed, this does not eliminate ambiguity in the determination of
collision forces, which requires the knowledge of friction characteristics at
the edges of interacting plates, rheological properties of rocks in the
collision zone, etc. In this context, the existing conclusions concerning the
amount of collision force effect on the stress state of the Western Europe
lithosphere appear to be insufficiently substantiated and any steps decreasing
the arbitrariness in estimates of these forces are beneficial. Without a more
accurate determination of collision forces, the discussion about relative
contributions of driving forces to the development of the stress field in
Western Europe (see paragraph 1.2) remains, in essence, pointless. This work
provides significant constraints on collision forces without invoking kinematic
characteristics of the Africa-Europe convergence. Provided that the
SH, max stress
direction is known in the region, these constraints are obtained from the
equilibrium conditions of the Western Europe lithosphere.
2. Formulation of the Problem
The nearly horizontal orientation of two from the three principal axes of the
stress tensor
T, mentioned in paragraph 1.1, admits the formulation of a 2-D
problem for modeling the tectonic stresses in Western Europe. I propose a
basically new approach to the solution of the problem in which experimentally
determined directions of
SH, max are used as input information rather than
restraints on the sought-for solution.
The region 0ABC in which the problem is stated includes the WESP province
(Figure 2)
and is bounded by MAR (its smoothed segment is shown as the curve 0
A in Figure 2)
to the west and by a boundary segment between the African and
Eurasian plates (curve 0C in Figure 2) to the south. The southern boundary 0
C coincides with that used in
[Gölke and Coblenz, 1996].
Like some other authors
[Ahorner, 1975;
Grünthal and Stromeyer, 1992;
Müller et al., 1992,
1997],
I assume that the sought-for 2-D field of tectonic stresses
in Western Europe is due to two forces: the push from MAR and the collision
force applied at the southern boundary and produced by the convergence of Africa
and Europe.
These forces are modeled as stress vectors
tR and
tC distributed, respectively, on the curves 0
A and 0C (Figure 2). (note 4)
It is reasonable to assume
that the modulus
| tR|=pR is constant along the MAR axis
[Parsons and Richter, 1980;
Richardson, 1992].
Let
kR and
kC be the directing unit vectors of
tR and
tC, and let
pC be the value of the collision stresses; then
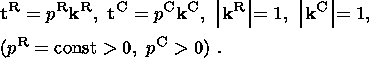 | (1) |
The horizontal vectors
tR and
tC are directed inside the study region,
producing normal stresses at the western and southern boundaries,
so that
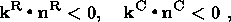 | (2) |
where
nR and
nC are unit vectors of the outer normal to the respective
boundaries of the region (Figure 2) and the symbol " " means the scalar product of
vectors. The mass forces due to lateral density inhomogeneities in the
lithosphere are neglected in this work.
" means the scalar product of
vectors. The mass forces due to lateral density inhomogeneities in the
lithosphere are neglected in this work.
In view of the aforesaid concerning the uniform orientation
of the maximum
compressive stress in the study region, a homogeneous field of straight
trajectories of
SH, max striking at an azimuth of
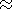 325o (Figure 2) is constructed;
this value is the average strike azimuth of experimentally determined maximum
compression axes (see Section 1.2). It is assumed that this field of
trajectories can be extended into the western and northwestern oceanic areas of
the study region 0ABC. The Cartesian coordinate system associated with the
constructed field of principal stress trajectories has its origin at the
intersection point of the bounding curves 0A and 0B; the
x1 axis coincides
in direction with the
SH, max trajectories, and the
x2 axis is directed along
trajectories of the minimum compression
SH, min (Figure 2). Evidently, the unit
vectors
m1 and
m2 of the principal axes of the sought-for tensor
T are
spatially invariable and are directed along
x1 and
x2, respectively. Given
the field of trajectories of a 2-D stress tensor, the latter can be determined
by integrating equilibrium equations without invoking information on rheological
properties of the lithosphere; the equilibrium equations form a closed system of
hyperbolic-type differential equations with characteristics coinciding with the
trajectories of principal stresses
[Mukhamediev, 1991].
325o (Figure 2) is constructed;
this value is the average strike azimuth of experimentally determined maximum
compression axes (see Section 1.2). It is assumed that this field of
trajectories can be extended into the western and northwestern oceanic areas of
the study region 0ABC. The Cartesian coordinate system associated with the
constructed field of principal stress trajectories has its origin at the
intersection point of the bounding curves 0A and 0B; the
x1 axis coincides
in direction with the
SH, max trajectories, and the
x2 axis is directed along
trajectories of the minimum compression
SH, min (Figure 2). Evidently, the unit
vectors
m1 and
m2 of the principal axes of the sought-for tensor
T are
spatially invariable and are directed along
x1 and
x2, respectively. Given
the field of trajectories of a 2-D stress tensor, the latter can be determined
by integrating equilibrium equations without invoking information on rheological
properties of the lithosphere; the equilibrium equations form a closed system of
hyperbolic-type differential equations with characteristics coinciding with the
trajectories of principal stresses
[Mukhamediev, 1991].
In the case of a homogeneous field of straight trajectories and vanishing
horizontal mass forces, the general solution providing extreme horizontal
tectonic stresses has the form
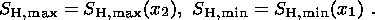 | (3) |
As seen from (3),
SH, max does not depend on
x1, and
SH, min does not depend on
x2. General solution (3) needs some comments. The integration of
3-D
equilibrium equations of the medium gives
[Mukhamediev, 1991]
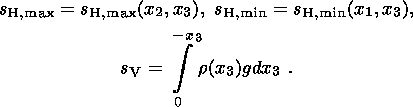 | (4) |
Here,
sH, max and
sH, min are, respectively, maximum and minimum local
horizontal
stresses,
sV(x3) is the vertical local principal stress,
x3 is the
vertical coordinate measured upward from the Earth's surface,
r is the
density of lithosphere, and
g is gravity. Formulas (4) were derived under the
assumption that no lateral anomalies of density are present and with due regard
to the fact that two principal stresses are nearly horizontal and their
directions are virtually independent of depth in the Western Europe lithosphere
(see Sections 1.1 and 1.2). Taking into account the conclusions made in
[McGarr, 1988]
concerning a hydrostatic stress state of the lithosphere in the
absence of applied tectonic forces, the local stresses
sH, max and
sH, min can be represented as the superpositions
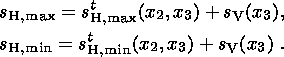 | (5) |
Here,
sH,maxt and
stH, min are maximum and minimum
horizontal tectonic stresses.
Integrating the complete local stresses over the lithosphere thickness
H yields
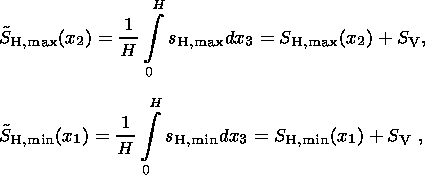 | (6) |
where
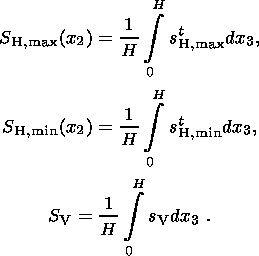 | (7) |
Solution (3) and subsequent analysis deal with exactly tectonic stresses
SH,max(x2) and
SH,min(x1) averaged over the lithosphere
thickness, satisfying 2-D equilibrium
equations and determined by relations (7). These stresses arise in response to
the action of horizontal tectonic forces and characterize the deviation of the
stress state from the hydrostatic state. The above representation of stresses is
possible due to the specific spatial pattern of the stress distribution in the
Western Europe lithosphere, and the averaging is necessary because the boundary
conditions of the problem are set just in terms of averaged tectonic stresses
(see Section 5 below).
To determine the unique solution from general solution (3), one should use the
boundary conditions at the western and southern boundaries of the study region,
which are not characteristics (and are nowhere tangent to the latter). On
specifying the distribution of the stress vector (and thereby the distribution
of principal stresses) on one of these boundaries (curve 0A or 0C ), a solution
of the Cauchy problem can be obtained in the curvilinear triangle 0AB or
0BC, respectively. Then one should solve a mixed problem in the remaining
triangle, with one condition (namely, the
SH, max distribution) specified on the
characteristic 0B from the solution of the preceding Cauchy problem and with
the second condition specified on the curvilinear boundary. Note that, since the
curves 0A and 0C are monotonic in the coordinate system ( x1, x2 ),
functions and vectors defined on the boundaries 0A and 0C can be represented
as a function of only one coordinate ( x1 or
x2 ). As required, one or another
representation will be used without changing the notation of pertinent functions
and vectors.
3. Solution of the Problem
I start with the solution of the Cauchy problem in 0AB because the push
forces, unlike the collision ones, are determined more reliably (e.g. see
[Parsons and Richter, 1980;
Richardson, 1992]).
Then, the following relation holds on 0A in accordance with (1):
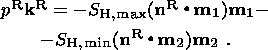 | (8) |
Defining on 0A the directing unit vector of stresses
kR as a function of
x2 (and therefore as a function of
x1 ) from condition (8) and using the
orthogonality of the unit vectors
m1 and
m2, the solution of the Cauchy
problem in the curvilinear triangle 0AB can be easily constructed. With
SH, max being independent of
x1, and
SH, min, of
x2, this solution has the form
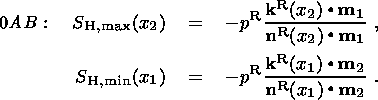 | (9) |
Now I find the solution in the curvilinear triangle 0BC. The solution obtained
in 0
AB is also valid on the characteristic 0B directed along the
x2 axis
(Figure 2).
The function
SH, max(x2) defined on the straight
line 0
B provides the
first boundary condition for the solution of the mixed problem in 0BC. The
second condition must be set on the southern boundary, i.e. on the
noncharacteristic line 0C. Note that, before doing this, continuity of the
stress vector on the characteristic 0B should be ensured by continuing, without
any changes, the function
SH, max(x2) defined in (9) into
the region 0BC. Thus,
the magnitude of the maximum compressive stress in the entire region 0ABC is
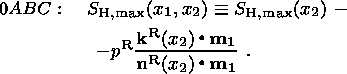 | (10) |
this value depends solely on the MAR axis geometry and push distribution pattern
along this axis and is independent of collision forces.
Based on solution (10), the stress vector on the southern boundary 0C can be
written as
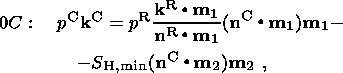 | (11) |
hence
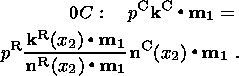 | (12) |
Relation (12) implies that, if the vector of boundary stresses
tR is specified
on the western boundary of the region, the projection of the collision stress
vector
tC m1 onto the axis of the maximum
compressive stress is fully
determined on the southern boundary. Consequently, in order to determine
SH, min in
the curvilinear triangle 0BC, it is sufficient to specify on 0C either the
direction
kC of the stress vector
tC or its modulus
pC.
m1 onto the axis of the maximum
compressive stress is fully
determined on the southern boundary. Consequently, in order to determine
SH, min in
the curvilinear triangle 0BC, it is sufficient to specify on 0C either the
direction
kC of the stress vector
tC or its modulus
pC.
1
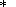 . Let the vector function
kC(x2) be given on 0C. Then, the modulus of the stress
produced by the Africa-Europe convergence is determined on the southern boundary
from (12):
. Let the vector function
kC(x2) be given on 0C. Then, the modulus of the stress
produced by the Africa-Europe convergence is determined on the southern boundary
from (12):
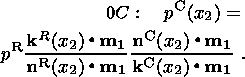 | (13) |
In this case, the distribution of the minimum compressive stress in the region
0
BC is found from (11):
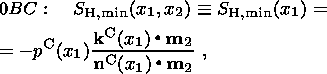 | (14) |
where the function
pC(x1) is calculated from the function
pC(x2) given by (12).
Formulas (10) and (14) provide the solution of the mixed problem in the region
0
BC. To make the solution continuous in the entire region 0ABC, the
following condition must be satisfied:
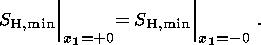 | (15) |
Based on (9) and (14), condition (15) takes the form
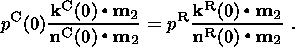 | (16) |
Using (13), this equality can be written as the condition
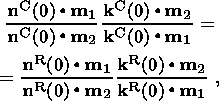 | (17) |
which must be satisfied at the origin of coordinates ( x1=0,
x2 = 0 ).
The complete solution in the study region is given by formulas (9), (10) and
(14) provided that condition (16) or (17) is satisfied.
2
 . Let the function
pC(x1) be specified on 0C. Then (12) defines the
directing vector of collision stresses on the boundary 0C:
. Let the function
pC(x1) be specified on 0C. Then (12) defines the
directing vector of collision stresses on the boundary 0C:
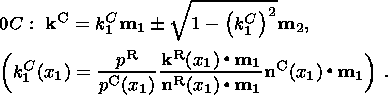 | (18) |
The solution of the mixed problem in 0BC, as before, is determined by formulas
(10) and (14), and the projection
kC(x1) m2 of
the directing unit vector of
stresses onto the
SH, min axis in (14) is calculated from (18). As
in the previous
case, the complete solution in 0ABC is given by formulas (9), (10) and (14),
complemented with the stress continuity condition (16) or (17).
m2 of
the directing unit vector of
stresses onto the
SH, min axis in (14) is calculated from (18). As
in the previous
case, the complete solution in 0ABC is given by formulas (9), (10) and (14),
complemented with the stress continuity condition (16) or (17).
4. Results of the Solution
Specifying the push force, actually distributed over a zone around MAR, on the
MAR segment 0
A allows one to choose, within certain limits, its direction
kR.
For example, supposing that a linear push is orthogonal to the ridge axis (i.e.
kR=- nR ), (9) implies that the hydrostatic
stress field in the region 0
AB is
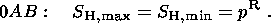 | (19) |
Below, I address the case of a ridge push coinciding in direction with the
maximum compressive stress:
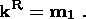 | (20) |
Then, as follows from (10), the magnitude of the maximum compressive stress in
the entire region 0
ABC is determined, irrespective of the collision forces, by
the expression
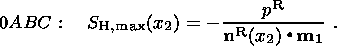 | (21) |
In this case, the region 0
AB is subjected to the uniaxial compression:
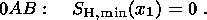 | (22) |
The function
SH, min(x1) in 0BC is determined by formula (14). In accordance
with (14) and (22), the continuity of solution (15) takes the form
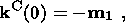 | (23) |
and the value of collision stresses is determined from (13) and (20):
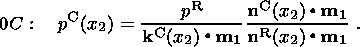 | (24) |

|
|
Figure 3
|
The function
SH, max(x2) in the WESP region
(the rectangle
BB D
D D in Figures 1 and
2) is plotted in Figure 3. After
Gölke and Coblenz [1996],
I set the modulus of the stress vector on the boundary 0A to be
pR = 25 MPa. This
value is based on model push estimates (e.g. see
[Parsons and Richter, 1980]).
D in Figures 1 and
2) is plotted in Figure 3. After
Gölke and Coblenz [1996],
I set the modulus of the stress vector on the boundary 0A to be
pR = 25 MPa. This
value is based on model push estimates (e.g. see
[Parsons and Richter, 1980]).

|
|
Figure 4
|
The direction of the stress vector
tC in the collision zone is defined as
follows. Let
b be the angle measured counterclockwise from
the positive
direction of the
x2 axis to the collision force direction
kC at the southern
boundary 0
C (Figures 4a,
4b,
4c).
I consider the case when the angle
b is a
linear function of
x2:
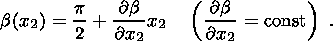 | (25) |
Relation (25) meets stress continuity condition (23). If
the gradient
 b/
b/ x2 is
negative (positive), the collision force vector
tC rotates clockwise
(counterclockwise), as a point on 0C moves from 0 to
C (Figures 4a,
4c).
The
case
x2 is
negative (positive), the collision force vector
tC rotates clockwise
(counterclockwise), as a point on 0C moves from 0 to
C (Figures 4a,
4c).
The
case
 b/
b/ x2 = 0 means that the vector
tC is directed along the axis of the
maximum compressive stress
SH, max everywhere on 0C.
x2 = 0 means that the vector
tC is directed along the axis of the
maximum compressive stress
SH, max everywhere on 0C.
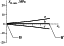
|
|
Figure 5
|
Concrete calculations were conducted for the following three gradients of the
angle
b along the
x2 axis:
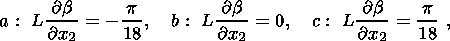 | (26) |
here
L is the length of 0B. The magnitude of the collision stresses
pC on the
segment
D C of the southern
boundary (Figure 2)
calculated from (24) is plotted
as a function of
x2 in Figure 4d. The difference between the functions
pC(x2) calculated at different values of the
gradient
C of the southern
boundary (Figure 2)
calculated from (24) is plotted
as a function of
x2 in Figure 4d. The difference between the functions
pC(x2) calculated at different values of the
gradient
 b/
b/ x2 from (26) is too small to be
reflected in Figure 4d. By contrast the stress
SH, min is much more sensitive to
small variations in
x2 from (26) is too small to be
reflected in Figure 4d. By contrast the stress
SH, min is much more sensitive to
small variations in
 b/
b/ x2 around zero. Figure 5 plots WESP values of the function
SH, min(x1) calculated from (14)
for three
x2 around zero. Figure 5 plots WESP values of the function
SH, min(x1) calculated from (14)
for three
 b/
b/ x2 values (26). Negative values of
x2 values (26). Negative values of
 b/
b/ x2 result in positive stresses
SH, min, whereas positive values of
x2 result in positive stresses
SH, min, whereas positive values of
 b/
b/ x2 give rise
to tensile stresses in the WESP region ( SH, min<0 ). The absolute value of
SH, min increases in the SE direction. If the collision
forces coincide in direction
with
SH, max (case (b) in (26)), a uniaxial compression
state ( SH, min = 0 )
independent of the
pC value arises in WESP, as well as in the entire region
0
ABC
x2 give rise
to tensile stresses in the WESP region ( SH, min<0 ). The absolute value of
SH, min increases in the SE direction. If the collision
forces coincide in direction
with
SH, max (case (b) in (26)), a uniaxial compression
state ( SH, min = 0 )
independent of the
pC value arises in WESP, as well as in the entire region
0
ABC

|
|
Figure 6
|
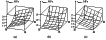
. Figure 6
(a, b, c) presents the WESP stress fields corresponding to the
spatial variations in
SH, max and
SH, min shown in Figures 3 and 5. The stresses
SH,max and
SH, min are shown as arrows whose length is proportional
to the modulus of the
respective stress. The stresses shown in Figures 6a, 6b and 6c were calculated at
positive, zero and negative values of
 b/
b/ x2, respectively.
x2, respectively.
|
|
Figure 7
|
Figure 7 presents the WESP ( BB D
D D in Figures 1 and 2) fields of the maximum
shear stress
tmax(x1, x2)
= (SH, max - SH, min)/2
for three
D in Figures 1 and 2) fields of the maximum
shear stress
tmax(x1, x2)
= (SH, max - SH, min)/2
for three
 b/
b/ x2 value (26).
x2 value (26).
The above results will change only insignificantly if the magnitude of collision
stresses
pC(x2) is given on the southern boundary 0
C, and their direction
kC is sought for when solving the problem. In conclusion, note
the replacement
of the real MAR trajectory (western boundary of the study region) by the
smoothed curve 0
A (Figure 2)
has also a weak effect on the model results.
5. Discussion of the Problem Statement and Solution
Results

|
|
Figure 8
|
Now I compare the approach to the determination of tectonic stress fields
proposed in this work with the approach based on traditional methods of
mathematical modeling. The stress field in Western Europe was numerically
modeled by
Gölke and Coblenz
[1996],
who solved a plane problem of the elasticity theory with various sets of boundary
conditions. The inferred solution was considered successful if model directions of
SH, max were consistent with their experimental
determinations. In all of the models,
displacements on the eastern boundary (which was not considered in the present work)
were set at zero. In two models, zero displacements were also specified on the southern
boundary (Figure 8).
Collision forces were applied at the southern boundary in the
other models.
Gölke and Coblenz [1996]
state that the choice of boundary conditions on the
eastern and southern boundaries affects only slightly the orientation and
magnitude of the modeled stress
SH, max. The authors themselves believe that the
choice of zero displacements on the eastern boundary is unrealistic but is
nevertheless justified by the fact that the model directions of
SH, max are
reasonably consistent with the general tendencies of the measured stress
directions. The stress state of the WESP lithosphere obtained by
Gölke and Coblenz [1996]
is close to a uniaxial one, and their resulting stress has a
value of about 25 MPa and a direction close to the global NW axis of maximum
compression observed in the WESP region. Thus, the results
of
Gölke and Coblenz [1996]
are similar to those obtained in my work for the case of coinciding
directions of the collision force
tC and
SH, max axis (Figures 3, 4b, 5 (curve b) and 6b).
However, basic distinctions exist between the approaches compared:
- Gölke and Coblenz are compelled to model
the eastern boundary of the region as
a rigid inset, whereas my approach does not require setting boundary conditions
at this boundary segment;
- in terms of the approach developed in this paper, the distribution of the
collision stress vector is constrained within narrow limits by the model
solution itself rather than specified on the basis of certain model
considerations as is done by
Gölke and Coblenz [1996];
- unlike the approach of these authors, in which an elastic, isotropic and
mechanically homogeneous model is adopted, the present work does not use any
constitutive relations at all.
These distinctions need additional comments. The classical formulation of the
problem used by
Gölke and Coblenz [1996]
implies that integral constraints can
only be imposed on the stresses acting along the eastern and southern boundaries
of the region studied. If the push is known, the resultant vector and moment of
these stresses are determined solely by the equilibrium conditions of the plate
as a whole. On the contrary, the approach developed here allows one to specify
the collision forces differentially, i.e. at each point of the southern boundary
0
C. Moreover, if the field of
SH, max trajectories is known throughout the region
0
ABC (Figure 2), the constraints imposed on the collision forces
tC(x2) by
equilibrium conditions, the continuity condition of solution (15), the condition
SH, minH, max and data
on the spatial pattern of the stress regime are much more
stringent than can seem at first glance. In particular, the vector
tC can
deviate only insignificantly from the
SH, max direction: if the angle
b in
(25) becomes much smaller than
p/2, the condition
SH, minH, max is violated.
Given a
linear dependence of
b on
x2 chosen in (26), this condition is violated
(in the southeastern part of the region 0ABC ) if
 b/
b/ x2<-p/9L.
x2<-p/9L.
The choice of the elastic model of lithosphere allows the application of a
nontraditional approach in which experimental data on the orientations of
principal horizontal stresses are used as input information rather than
constraints on the sought-for solution as is done in
[Gölke and Coblenz, 1996].
Data on the
SH, max orientation in the WESP region are used
for constructing the
field of straight trajectories, and the fields of
SH, max(x1, x2)
and
SH, min(x1, x2)
are determined by solving equations of the elasticity theory
without invoking any evidence on boundary stresses
[Mukhamediev, 2000;
Mukhamediev and Galybin, 2001].
The solution for the stress field is obtained up to five
arbitrary constants whose values can be defined from several instrumental
measurements of stresses.
The above property of the elastic problem solution indicates that stress
orientations provide relatively weak constraints on the sought-for solution.
Actually, by varying the arbitrary constants and leaving the stress orientation
unchanged at any point, fields of
SH, max and
SH, min significantly differing both
quantitatively and qualitatively can be obtained everywhere, including the
boundaries of the study region
[Mukhamediev and Galybin, 2001].
Therefore, stress fields with the same stress trajectories can be obtained with markedly
different sets of boundary conditions. This property may account for the
aforementioned weak dependence of the solution obtained in
[Gölke and Coblenz, 1996]
on the conditions set at the southern and eastern boundaries of Western
Europe. Moreover, this by no means guarantees that at least one of the sets of
boundary conditions employed in
[Gölke and Coblenz, 1996]
adequately approximates reality.
The necessity of an a priori choice of constitutive relations for the
lithosphere material can also be regarded as a limitation of the traditional
approach to the theoretical modeling of stress fields. Although an elastic model
appears quite adequate for stable blocks of the lithosphere, it is not free from
some internal contradictions. Using the determination of the stress state of the
Western Europe as an example, these contradictions can be characterized as
follows.
- First, experimental information on stress orientations is mostly gained by
using seismological data on focal mechanisms, i.e. irreversible fault motions in
the crust. In other words, although the lithosphere is assumed to be elastic,
data on its inelastic deformations are largely invoked.

|
|
Figure 9
|
- Second, there exist spatial distributions of principal
stress orientations that
are inconsistent with an elastic lithosphere. Thus, if stresses of second order
are taken into account, the Western Europe stress state is characterized by a
homogeneous field of straight trajectories overprinted by regional disturbances
due to the presence of large geological structures such as the Alps (see
Section 1.2). However, such a field of trajectories is inconsistent with a
plane problem of the elasticity theory. Actually, surrounding a disturbed area
by an arbitrary smooth contour
G lying completely within the homogeneity
region of the trajectories (Figure 9), one can show that the uniqueness of the
solution of the elastic problem within the contour requires linearity of the
trajectories
[Galybin and Mukhamediev, 1999].
This is at variance with the assumption on the presence of a local inhomogeneity
embedded in the field of straight trajectories.
The second comment implies that characteristic features of
the Western Europe
stress field on a regional scale cannot be obtained in terms of elastic problems
irrespective of boundary conditions. In particular, no regional disturbances in
the
SH, max directions are present in the solution presented
by
Gölke and Coblenz [1996]
(see Figure 8).
The present paper also presents a solution of the global
stress field with no regional disturbances. However, as distinct from the work
[Gölke and Coblenz, 1996],
the approach developed here is basically applicable
to arbitrarily structured fields of trajectories. If regional disturbances in
stress trajectories are taken into account, the algorithm of solving the problem
is significantly complicated as compared with that used above and should involve
the solution of several hyperbolic-type boundary problems with continuity
conditions imposed to link the solutions. Note also that, unlike the work
[Gölke and Coblenz, 1996],
the lithosphere can be anisotropic and mechanically
inhomogeneous within the framework of the approach proposed here.
The results of the present work demonstrate the potential of this approach in
determining the tectonic stress fields and reducing the arbitrariness in
estimates of forces driving lithospheric plates. These results should be
regarded as a first approximation to the reconstruction of real stress fields in
Western Europe. Actually, they depend, to an extent, on the assumption that the
field of straight trajectories of principal stresses can be extrapolated into
oceanic parts of the study region 0ABC. This simplifying assumption is not the
best one because it leads to the appearance of shear stresses on the MAR
trajectory. The subject of my future studies is the analysis of a model that
includes, among other improvements, a weaker assumption on the pattern of
trajectories in oceanic parts of the lithosphere and the examination of the
stress field variation with depth. However, the main results of the present
work, primarily those concerning the
SH, max field, will not change
substantially.
The
SH, max magnitudes are transmitted from the ridge
along
characteristics ( SH, max trajectories) without any significant changes,
if the
field of curvilinear characteristics in oceanic parts does not contain areas of
their condensation and rarefaction. (note 5)
Likewise, the model changes will not affect the validity of such a basic result as
the change in
sign of the
SH, min value associated with a westward or eastward
deviation of the
collision stress vector
tC from the direction of
SH, max. However, it is
possible that
SH, min will not change its sign simultaneously
throughout the WESP
territory.
The solution presented in this paper was obtained for tectonic stresses averaged
over the lithosphere thickness
H 100 km. This is mainly due to
the fact that
the boundary stresses
pR refer to exactly this thickness of lithosphere.
Because of the averaging of stresses, the inferred model solution cannot be
directly compared with the observed depth variations of stress magnitudes and
stress regime types. However, the comparison between lateral variations in the
model stress field and experimental data leads to quite definite conclusions
about the collision force orientation pattern and magnitudes of the related
tectonic stresses. Instrumental measurements of near-surface stresses indicate
that the magnitude of the minimum horizontal stress in the northern and central
WESP parts is often close to zero or negative (on the order of
- 1 to
- 3 MPa)
[Becker and Davenport, 2001;
Froidevaux et al., 1980].
These results indicate
the tectonic stress
SH, min to be tensile, and therefore the solution
presented
in Figure 6c
is most consistent with experimental data. It is likewise consistent
with data on the spatial pattern of the stress regime, according to which the
strike-slip faulting regime prevails in the WESP territory (see Section 1.2).
The solution shown in Figure 6a complies with a compression regime in the WESP
region. Note also that a decrease in
SH, max in the NE direction and a decrease
in the negative value of
SH, min in the SE direction make the stress regime
close
to a tensile one in the northern Apennines region. Focal mechanisms of
earthquakes in this region provide the most reliable evidence of an extension
regime here (see Section 1.2). The model values of the maximum shear stress
tmax in this
region also reach a local extremum (Figure 7c). Thus, experimental
data on the magnitude and regime of stresses indicate that the direction of the
collision stresses
tC is close to that of
SH, max and rotates counterclockwise
when moving along the southern boundary in the eastward direction (Figure 4c).
100 km. This is mainly due to
the fact that
the boundary stresses
pR refer to exactly this thickness of lithosphere.
Because of the averaging of stresses, the inferred model solution cannot be
directly compared with the observed depth variations of stress magnitudes and
stress regime types. However, the comparison between lateral variations in the
model stress field and experimental data leads to quite definite conclusions
about the collision force orientation pattern and magnitudes of the related
tectonic stresses. Instrumental measurements of near-surface stresses indicate
that the magnitude of the minimum horizontal stress in the northern and central
WESP parts is often close to zero or negative (on the order of
- 1 to
- 3 MPa)
[Becker and Davenport, 2001;
Froidevaux et al., 1980].
These results indicate
the tectonic stress
SH, min to be tensile, and therefore the solution
presented
in Figure 6c
is most consistent with experimental data. It is likewise consistent
with data on the spatial pattern of the stress regime, according to which the
strike-slip faulting regime prevails in the WESP territory (see Section 1.2).
The solution shown in Figure 6a complies with a compression regime in the WESP
region. Note also that a decrease in
SH, max in the NE direction and a decrease
in the negative value of
SH, min in the SE direction make the stress regime
close
to a tensile one in the northern Apennines region. Focal mechanisms of
earthquakes in this region provide the most reliable evidence of an extension
regime here (see Section 1.2). The model values of the maximum shear stress
tmax in this
region also reach a local extremum (Figure 7c). Thus, experimental
data on the magnitude and regime of stresses indicate that the direction of the
collision stresses
tC is close to that of
SH, max and rotates counterclockwise
when moving along the southern boundary in the eastward direction (Figure 4c).
In light of the results of this work, the discussion on the
relative
contributions of driving forces to the tectonic stresses in the Western Europe
lithosphere (see Section 1.2) can be complemented by specific considerations.
Let a homogeneous system of stress orientations be known from observations, as
is the case in this study.
The stress magnitudes are then fully determined by
the MAR push in northwestern Europe (0AB in
Figure 2) and by the Africa-Europe
collision forces in southwestern Europe (0BC in Figure 2). (note 6)
However, the continuity of the stress field (on the line 0
B, see Figure 2) implies
that the push and collision forces are coupled. Therefore, both forces equally
contribute to the formation of the tectonic stress field, although the method of
solving the problem described in Section 3 might induce one to believe that
the
push force prevails.
Both the above conclusion and the solution presented in this paper were derived
under the assumption of smallness of the resultant force
Tb produced by shear
stresses
tb at the base of lithosphere.
There is not agreement concerning
the origin of the stresses
tb. Some researchers believe
that these stresses are
due to active mantle flows generally inducing the motion of continents (e.g. see
[Trubitsyn and Rykov, 1998]).
Under special assumptions on properties of the
tb distribution over the base
of lithosphere, the force
Tb can
significantly exceed the push
[Karakin, 1998].
According to other concepts based
on the analysis of in situ stress indicators, the force
Tb is, on the
contrary, a resistance force exerted by the underlying mantle on the
lithospheric plate
[Richardson, 1992;
Zoback, 1992;
Zoback et al., 1989].
The related stresses
tb are estimated to be small
(  10-2 MPa)
[Richardson, 1992].
When solving mathematical modeling problems of intraplate stresses,
the force
Tb is either neglected
(e.g. see [Gölke and Coblenz, 1996]) or its value and
direction are found from mechanical balance of forces applied to the plate under
the simplifying assumption of invariability of the stress
tb along the
base of lithosphere
[Cloetingh and Wortel, 1985;
Coblentz et al., 1998].
10-2 MPa)
[Richardson, 1992].
When solving mathematical modeling problems of intraplate stresses,
the force
Tb is either neglected
(e.g. see [Gölke and Coblenz, 1996]) or its value and
direction are found from mechanical balance of forces applied to the plate under
the simplifying assumption of invariability of the stress
tb along the
base of lithosphere
[Cloetingh and Wortel, 1985;
Coblentz et al., 1998].
The solution obtained in Sections 3 and 4 of this paper is readily generalized
to incorporate the stresses
tb. Really, let constant shear
stresses
tb be
uniformly distributed over the base of lithosphere and let they be oriented
parallel to the
SH, max axis. (note 7)
Then, given active convective flows in the mantle with the stresses
tb directed from MAR to the
collision zone, expression (10) for the stress
SH, max will contain an additional term accounting
for a linear increase in
SH, max with
increasing
x1. The magnitude of the collision stresses
pC will accordingly
increase. On the contrary, if the underlying mantle offers a resistance to the
plate motion, the stress magnitudes
SH, max in (10) experience an additional
decrease that is linear in
x1 and is accompanied by a decrease in
pC. Note
however that absolute velocities of the Eurasian plate are much smaller compared
to any of the other lithospheric plates
[Gripp and Gordon, 1990;
Richardson, 1992].
Therefore, the approximation adopted here and consisting in vanishing
stresses
tb at the base of lithosphere
is most suitable for the study of
tectonic stresses in the Eurasian plate.
Conclusion
1. As is evident from experimental data, the direction of the maximum
compressive stress
SH, max over the most territory of Western Europe
is invariable
both laterally and in depth. A uniform global NW orientation of the
SH, max axis is
reflected in general characteristics of seismicity and jointing patterns of
sedimentary rocks and accounts for specific features of the development of some
neotectonic structures in the Western Europe lithosphere.
2. A widely accepted assumption consists in that tectonic stresses of first
order in the lithosphere of the region are controlled by the push from MAR and
by the collision forces in the Africa-Europe convergence zone. This assumption
cannot be rigorously substantiated because data on the value and direction of
the collision force are controversial. Estimation of collision forces is usually
based on the Africa-Europe convergence kinematics which cannot be reliably
reconstructed at present both by direct methods of satellite geodesy (due to
inadequate density of the measurement network in the western and central
Mediterranean) and on the basis of geological-geophysical models (due to
restrictive assumptions involved in the reconstructions). However, even if a
reliable kinematic reconstruction is available, the transition from movements
and deformations in the collision zone to the related active forces requires
additional assumptions on constitutive relations.
3. The application of traditional methods to the mathematical modeling of the
stress state requires the knowledge of constitutive relations for the
lithosphere material. Determination of stresses in Western Europe (as well as in
other stable blocks of lithosphere) is usually based on relations of the linear
elasticity theory. However, the model of a linear elastic body is basically
ineffective in modeling local disturbances of the local uniform orientation of
SH, max that are produced by large geological structures
such as the Alps and are
typical of the stress state of the Western Europe lithosphere. This statement is
based on the fact that a 2-D deformation of a homogeneous isotropic elastic body
precludes local disturbances in the field of straight trajectories of principal
stresses, which was proven in this work.
4. Apart from the knowledge of rheological properties of lithosphere, the
traditional approach requires boundary conditions to be set on the entire
perimeter of the region. In particular, this necessitates adopting hypotheses on
the behavior of stresses and/or displacements on a conventional line bounding
Western Europe to the east that is not an interplate boundary. Moreover, poorly
constrained stresses should be specified on the southern boundary (in the
collision zone). All of the aforementioned boundary conditions are chosen so as
to bring into agreement the model and experimentally constrained directions of
SH, max at points where the latter have been determined.
However, even the
coincidence of theoretical and experimental directions of
SH, max does not guarantee
the uniqueness and validity of the inferred stress field because it is still
fairly sensitive to the choice of boundary stress magnitudes.
5. The direct approach developed in this paper for the determination of the
field of the tectonic stress tensor uses experimental data on the
SH, max orientation as input information. These data
are employed for constructing the
global field of straight trajectories of
SH, max which is extrapolated into oceanic
lithosphere zones adjacent to the continental Western Europe and for solving a
hyperbolic-type problem of integrating the equilibrium equations. Such a
formulation of the problem does not require postulating rheological properties
of the lithosphere (in particular, the lithosphere can be anisotropic and
mechanically inhomogeneous). Moreover, it is not necessary to set boundary
conditions on the entire perimeter of the study region: the distribution of
stress vectors is only preset on a MAR axis segment ( tR ) and in the collision
zone ( tC ).
6. The solution of the problem on tectonic stresses in Western Europe made it
possible to determine the distribution of the projection of the collision stress
vector
tC onto the
SH, max direction at the southern boundary of the
region.
Certain additional conditions imposed on the solution lead to the important
conclusion on the similarity between the directions of
SH, max and
tC (in a long-wavelength approximation). Importantly, the restraint
imposed on the collision
stresses is derived directly from equilibrium conditions rather than from the
kinematic analysis of the Africa-Europe convergence.
7. The model stress field in the WESP region shows that the
SH, max value
decreases in the NE direction, whereas the
SH, min modulus increases in the SE
direction. The spatial distribution pattern of the
SH, min value is fairly
sensitive to the
tC direction: the
SH, min stress is compressive, zero or
tensile depending on whether the collision stress vector
tC deviates westward
from, coincides with or deviates eastward from the
SH, max direction. Apparently
this conclusion is not critically contingent on the assumption of linearity of
the principal stress trajectories in oceanic areas adjacent to Western Europe.
8. The choice of the actual direction of
tC should be based on the comparison
between theoretically and experimentally determined stress regimes of the
Western Europe lithosphere, including instrumental measurements of stresses that
provide reliable constraints on
SH, max and
SH, min. Such a comparison showed that
the stresses
tC are close in direction to the
SH, max axis and experience a
counterclockwise rotation on the southern boundary in the eastward direction. It
is exactly this pattern of the collision stresses that accounts for the presence
of the observed tensile stresses
SH, min and strike-slip faulting regime in most
of the WESP territory.
9. The solution obtained in this work shows that the push and collision forces
contribute equally to the formation of the tectonic stress field in Western
Europe. The stresses at the base of lithosphere accommodating the convective
flows in the mantle do not appear to have a significant effect on this field.
10. As distinct from traditional methods, the approach developed in this work
is
potentially promising for the modeling of second-order stresses responsible for
local disturbances in the global stress field.
Acknowledgments
This work was supported in part by the Russian Foundation for Basic
Research, project no. 01-05-64158.
References
Ahorner, L., Present-day stress field and seismotectonics block movements along
major fault zones in western Europe, Tectonophysics, 29, 223-249, 1975.
Albarello, D., E. Mantovani, D. Babucci, and C. Tamburelli, Africa-Eurasia
kinematics: main constraints and uncertainties, Tectonophysics, 243, 25-36,
1995.
Amadei, B., and O. Stephanson, Rock stress and its measurement, London:
Chapman & Hall, 1997.
Anderson, E. M., The dynamics of faulting and dyke formation with applications
to Britain, Edinburgh: Oliver and Boyd, 1951.
Andeweg, B., G. De Vicente, S. Cloetingh, J. Giner, and A. Mu
n oz Martin, Local
stress fields and intraplate deformation of Iberia: variations in spatial and
temporal interplay of regional stress sources, Tectonophysics, 305, 153-164,
1999.
Argus, D. F., R. G. Gordon, C. DeMets, and S. Stein, Closure of the Africa
- Eurasia-North
America plate motion circuit and tectonics of the Gloria fault,
J. Geophys. Res., 94, (B), 5585-5602, 1989.
Balling, N., and E. Bauda, Europe's lithosphere - recent activity, in A continent
revealed, The European geotraverse, p. 111-137, Cambridge University
Press, 1992.
Becker, A., "In situ" stress data from the Jura Mountains - new results and
interpretation, Terra Nova, 11, 9-15, 1999.
Becker, A., and C. A. Davenport, Contemporary in situ stress determination at
three sites in Scotland and northern England, J. Struct. Geol., 23, 407-419,
2001.
Boncio, P., and G. Lavecchia, A structural model for active extension in Central
Italy, J. Geodynamics, 29, 233-244, 2000.
Campbell, J., and A. Nothnagel, European VLBI for crustal dynamics, J. Geodynamics,
30, 321-326, 2000.
Cloetingh, S., and R. Wortel, Regional stress field of the Indian plate,
Geophys. Res. Lett., 12, 77-80, 1985.
Coblentz, D. D., S. Zhou, R. R. Hillis, R. M. Richardson, and
M. Sandiford,
Topography, boundary forces, and the Indo-Australian intraplate stress field,
J. Geophys. Res., 103, (B), 919-931, 1998.
Collettini, C., M. Barchi, C. Pauselli, C. Federico, and G. Pialli,
Seismic
expression of active extensional faults in northern Umbria (Central Italy),
J. Geodynamics, 29, 309-321, 2000.
Cornet, F. H., and J. Yin, Analysis of induced seismicity for stress field
determination and pore pressure mapping, Pure Appl. Geophys., 145, 677-699,
1995.
Delouis, B., H. Haessler, A. Cisternas, and L. Rivera, Stress tensor
determination in France and neighbouring regions, Tectonophysics, 221, 413-438,
1993.
DeMets, C., R. G. Gordon, D. F. Argus, and S. Stein, Current plate
motions,
Geophys. J. Int., 101, 425-478, 1990.
De Vicente, G., G. L. Giner, A. Mu
n oz-Martin, J. M. Gonz
a les-Casado, and
R. Lindo, Determination of present-day stress tensor and neotectonic interval
in
the Spanish Central System and Madrid Basin, central Spain, Tectonophysics, 266,
405-424, 1996.
Eva, E., and S. Solarino, Variations of stress directions in the western Alpine
arc, Geophys. J. Int., 135, 438-448, 1998.
Eva, E., S. Pastore, and N. Deichmann, Evidence for ongoing extensional
deformation in the western Swiss Alps and thrust-faulting in the southwestern
Alpine foreland, J. Geodynamics, 26, 27-47, 1998.
Frepoli, A., and A. Amato, Spatial variation in stresses in peninsular Italy and
Sicily from background seismicity, Tectonophysics, 317, 109-124, 2000.
Froidevaux, C., C. Paquin, and M. Souriau, Tectonic stresses in France: in-situ
measurements with a flat jack, J. Geophys. Res., 85, (B), 6349-6346, 1980.
Galybin, A. N., and Sh. A. Mukhamediev, Plane elastic boundary value problem posed
on orientation of principal stresses, J. Mech. Phys. Solids, 47, 2381-2409,
1999.
Gapais, D., P. R. Cobbold, O. Bourgeois, D. Rouby, and M. Urreiztieta,
Tectonic
significance of fault slip data, J. Struct. Geology, 22, 881-888, 2000.
Gephart, J. W., and D. W. Forthsyth, An improved method for determining the
regional stress tensor using focal mechanisms data: applications to the San
Fernando earthquake sequence, J. Geophys. Res., 89, (B), 9305-9320, 1984.
Gölke, M., and M. Brudy, Orientation of
crustal stresses in the North Sea and
Barents Sea inferred from borehole breakouts, Tectonophysics, 266, 25-32,
1996.
Gölke, M., and D. Coblenz, Origins of the
European regional stress field,
Tectonophysics, 266, 11-24, 1996.
Gripp, A. E., and R. G. Gordon, Current plate velocities relative to hotspots
incorporating the Nuvel-1 global plate motion model, Geophys. Res. Lett., 17,
1109-1112, 1990.
Greiner, G., In situ stress measurements in South West Germany, Tectonophysics,
29, 265-274, 1975.
Greiner, G., and J. H. Illies, Central Europe: active or residual stresses, Pure
Appl. Geophys., 115, 11-26, 1977.
Grob, H., K. Kovari, and C. Amstad, Sources of error in the determination of
in-situ
stresses by measurements, Tectonophysics, 29, 29-39, 1975.
Grünthal, G., and D. Stromeyer, The recent
crustal stress field in central
Europe: trajectories and finite element modeling, J. Geophys. Res., 97,
(B), 11,805-11,820, 1992.
Harper, T. R., and J. S. Szymanski, The nature and determination of stress in the
accessible lithosphere, Phil. Trans. R. Soc. London. Ser. A, 337, 5-24, 1991.
Illies, J. H., Recent and paleo-intraplate tectonics in stable Europe and the
Rhinegraben system, Tectonophysics, 29, 251-264, 1975.
Illies, H., and G. Greiner, Holocene movements and state of stress in the
Rhinegraben rift system, Tectonophysics, 52, 349-359, 1979.
Kahle, H.-G., C. Straub, R. Reilinger, S. McClusky, R. King, K. Hurst,
G. Veis,
K. Kastens, and P. Cross, The strain rate field in the eastern Mediterranean
region, estimated by repeated GPS measurements, Tectonophysics, 294, 237-252,
1998.
Karakin, A. V., An asymptotic decomposition technique as applied to geodynamic
models of the crust and lithosphere (in Russian), Geoinformatika, 34, 3-6,
1998.
Letouzev J., Cenozoic paleo-stress pattern in the Alpine Foreland and structural
interpretation in a platform basin, Tectonophysics, 132, 215-231, 1986.
McGarr, A., On the state of lithospheric stress in the absence of applied
tectonic forces, J. Geophys. Res., 93, (B), 13,609-13,617, 1988.
Montone, P., A. Amato, and S. Pondrelli, Active stress map of Italy,
J. Geophys. Res., 104, (B), 25,595-25,610, 1999.
Mukhamediev, Sh. A., Retrieving field of stress tensor in crustal blocks,
Izvestiya, Earth Physics, 27, (5), 370-377, 1991.
Mukhamediev, Sh. A., Reconstruction of tectonic stresses from fault slip motions:
Mathematical and physical constraints (in Russian), Dokl. RAN, 331, (4),
500-503, 1993.
Mukhamediev, Sh. A., Nonclassical boundary-value problems of the continuum
mechanics for geodynamics, Doklady, Earth Sciences, 373, (5), 918-922, 2000.
Mukhamediev, Sh. A. and A. N. Galybin, A direct approach to the determination of
regional stress fields: A case study of the West European, North American and
Australian platforms, Izvestia, Phys. Solid Earth, 37, 636-652, 2001.
Müller, B., M. L. Zoback, K. Fuchs,
L. Mastin, S. Gregersen, N. Pavoni,
O. Stefansson, and C. Ljunggren, Regional patterns of tectonic stress in
Europe,
J. Geophys. Res., 97, (B), 11,783-11,803, 1992.
Müller, B., V. Wehrle, H. Zeyen, and
K. Fuchs, Short-scale variations of
tectonic regimes in the western European stress province north of the Alps and
Pyrenees, Tectonophysics, 275, 199-219, 1997.
Noomen, R., T. A. Springer, B. A. C. Anbrosius, K. Herzberger,
D. C. Kuijper,
G. J. Mets, B. Overgaauw, and K. F. Wakker, Crustal deformations
in the Mediterranean
area computed from SLR and GPS observations, J. Geodynamics, 21, 73-96, 1996.
Parsons, B., and F. M. Richter, A relation between driving force and geoid
anomaly associated with the mid-ocean ridges, Earth Planet. Sci. Lett., 51,
445-450, 1980.
Plenefisch, T., and K. P. Bonjer, The stress field in the Rhine Graben area
inferred from earthquake focal mechanisms and estimation of frictional
parameters, Tectonophysics, 275, 71-97, 1997.
Ranalli, G., Geotectonic relevance of rock-stress determinations,
Tectonophysics, 29, 49-58, 1975.
Regenauer-Lieb, K., Plastic velocity vector diagrams applied to indentation and
transpression in the Alps, J. Geodynamics, 21, 339-353, 1996.
Reinecker, J., and W. A. Lenhardt, Present-day stress field and deformation in
eastern Austria, Int. J. Earth Sciences, 88, 532-550, 1999.
Richardson, R. M., Ridge forces, absolute plate motions, and the intraplate
stress field, J. Geophys. Res., 97, (B), 11,739-11,749, 1992.
Richardson, R. M., S. C. Solomon, and N. H. Sleep, Tectonic stress in the
plates,
Rev. Geophys., 17, 981-1019, 1979.
Rivera, L., and A. Cisternas, Stress tensor and fault plane solutions for a
population of earthquakes, Bull. Seismol. Soc. Am., 80, 600-614, 1990.
Rutqvist, J., C.-F. Tsang, and O. Stephansson, Uncertainty in the maximum
principal stress estimated from hydraulic fracturing measurements due to the
presence of the induced fracture, Int. J. Rock Mech. Min. Sci., 37, 107-120,
2000.
Savostin, L. A., J. C. Sibuet, L. P. Zonenshain, X. Le Pichon,
and M. J. Roulet,
Kinematic evolution of the Tethys belt from the Atlantic ocean to the Pamirs
since the Triassic, Tectonophysics, 123, 1-35, 1986.
Scotti, O., and F. H. Cornet, In-situ stress fields and focal mechanism solutions
in central France, Geophys. Res. Lett., 21, 2345-2348, 1994.
Trubitsyn, V. P., and V. V. Rykov, A self-consistent 2-D model of mantle
convection with a floating continent, Russian Journal of Earth Sciences, 1,
(1), 1-11,
1998.
Twiss, R. J., and J. F. Unrun, Analysis of fault slip inversions: do they
constrain stress or strain rate? J. Geophys Res. 103, (B), 12,209-12,222,
1998.
Wirput, D., and M. Zoback, Constraining the stress tensor in the Visund field,
Norwegian North Sea: Application to wellbore stability and sand production,
Int. J. Rock Mech. Min. Sci., 37, 317-336, 2000.
Yin, J. M, and F. H. Cornet, Integrated stress determination by joint inversion of
hydraulic tests and focal mechanisms, Geophys. Res. Lett., 21, 2645-2648,
1994.
Zoback, M. D., R. Apel, J. Baumgartner, et al., Upper-crustal strength inferred
from stress measurements to 6 km depth in the KTB borehole, Nature, 365,
633-635, 1993.
Zoback, M. L., First- and second-order patterns of stress in the lithosphere: the
world stress map project, J. Geophys. Res., 97, (B), 11,703-11,728, 1992.
Zoback, M. L., M. D. Zoback, J. Adams, et al., Global patterns of tectonic stress,
Nature, 341, 291-298, 1989.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on March 26, 2002.

 14o E
[Grünthal and Stromeyer, 1992;
Müller et al., 1992].
The
SH, max direction is virtually independent of depth
and is not affected by short-wavelength
variations in the thickness of the lithosphere, its structural features and topography
[Müller et al., 1992;
Richardson, 1992].
Large geological structures (e.g. the Alps) superimpose
regional signatures on the global orientation of the stresses
[Müller et al., 1992].
14o E
[Grünthal and Stromeyer, 1992;
Müller et al., 1992].
The
SH, max direction is virtually independent of depth
and is not affected by short-wavelength
variations in the thickness of the lithosphere, its structural features and topography
[Müller et al., 1992;
Richardson, 1992].
Large geological structures (e.g. the Alps) superimpose
regional signatures on the global orientation of the stresses
[Müller et al., 1992].
 26o
[Ahorner, 1975;
Grünthal and Stromeyer, 1992;
Illies and Greiner, 1979;
Müller et al., 1992,
1997;
Zoback, 1992;
Zoback et al., 1989];
26o
[Ahorner, 1975;
Grünthal and Stromeyer, 1992;
Illies and Greiner, 1979;
Müller et al., 1992,
1997;
Zoback, 1992;
Zoback et al., 1989];
 55o N including Fennoscandia and
characterized by a wide scatter in the azimuths of the
SH, max axis strike (300o
55o N including Fennoscandia and
characterized by a wide scatter in the azimuths of the
SH, max axis strike (300o
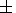 45o)
[Gölke and Brudy, 1996;
Müller et al., 1992;
Wirput and Zoback, 2000; and others];
45o)
[Gölke and Brudy, 1996;
Müller et al., 1992;
Wirput and Zoback, 2000; and others];
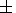 27o), with the normal and strike-slip
faulting regimes prevailing west and
east of
27o), with the normal and strike-slip
faulting regimes prevailing west and
east of
 30o E, respectively
[Gölke and Coblenz, 1996;
Müller et al., 1992,
1997;
Zoback et al., 1989].
30o E, respectively
[Gölke and Coblenz, 1996;
Müller et al., 1992,
1997;
Zoback et al., 1989].

 D
D D in Figures 1 and 2) is somewhat larger than the territory considered in
[Müller et al., 1992,
1997].
I discuss in more detail the spatial distribution of the stress state
characteristics in WESP and adjacent regions.
D in Figures 1 and 2) is somewhat larger than the territory considered in
[Müller et al., 1992,
1997].
I discuss in more detail the spatial distribution of the stress state
characteristics in WESP and adjacent regions.
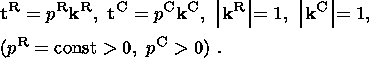
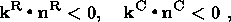
 " means the scalar product of
vectors. The mass forces due to lateral density inhomogeneities in the
lithosphere are neglected in this work.
" means the scalar product of
vectors. The mass forces due to lateral density inhomogeneities in the
lithosphere are neglected in this work.
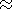 325o (Figure 2) is constructed;
this value is the average strike azimuth of experimentally determined maximum
compression axes (see Section 1.2). It is assumed that this field of
trajectories can be extended into the western and northwestern oceanic areas of
the study region 0ABC. The Cartesian coordinate system associated with the
constructed field of principal stress trajectories has its origin at the
intersection point of the bounding curves 0A and 0B; the
x1 axis coincides
in direction with the
SH, max trajectories, and the
x2 axis is directed along
trajectories of the minimum compression
SH, min (Figure 2). Evidently, the unit
vectors
m1 and
m2 of the principal axes of the sought-for tensor
325o (Figure 2) is constructed;
this value is the average strike azimuth of experimentally determined maximum
compression axes (see Section 1.2). It is assumed that this field of
trajectories can be extended into the western and northwestern oceanic areas of
the study region 0ABC. The Cartesian coordinate system associated with the
constructed field of principal stress trajectories has its origin at the
intersection point of the bounding curves 0A and 0B; the
x1 axis coincides
in direction with the
SH, max trajectories, and the
x2 axis is directed along
trajectories of the minimum compression
SH, min (Figure 2). Evidently, the unit
vectors
m1 and
m2 of the principal axes of the sought-for tensor
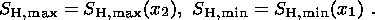
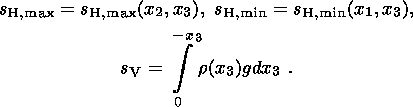
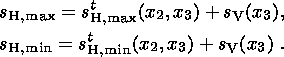
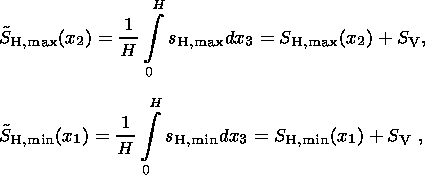
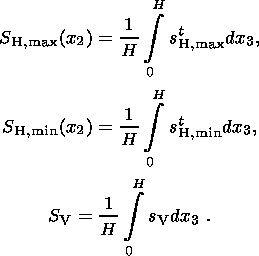
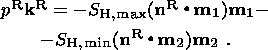
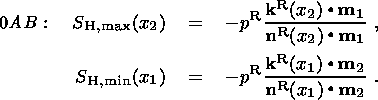
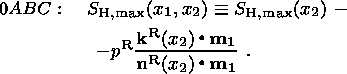
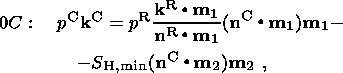
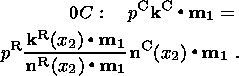
 m1 onto the axis of the maximum
compressive stress is fully
determined on the southern boundary. Consequently, in order to determine
SH, min in
the curvilinear triangle 0BC, it is sufficient to specify on 0C either the
direction
kC of the stress vector
tC or its modulus
pC.
m1 onto the axis of the maximum
compressive stress is fully
determined on the southern boundary. Consequently, in order to determine
SH, min in
the curvilinear triangle 0BC, it is sufficient to specify on 0C either the
direction
kC of the stress vector
tC or its modulus
pC. 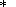 . Let the vector function
kC(x2) be given on 0C. Then, the modulus of the stress
produced by the Africa-Europe convergence is determined on the southern boundary
from (12):
. Let the vector function
kC(x2) be given on 0C. Then, the modulus of the stress
produced by the Africa-Europe convergence is determined on the southern boundary
from (12):
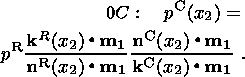
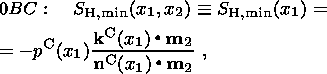
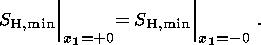
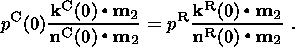
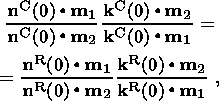
 . Let the function
pC(x1) be specified on 0C. Then (12) defines the
directing vector of collision stresses on the boundary 0C:
. Let the function
pC(x1) be specified on 0C. Then (12) defines the
directing vector of collision stresses on the boundary 0C: 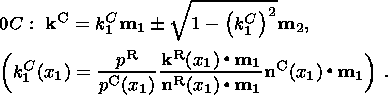
 m2 of
the directing unit vector of
stresses onto the
SH, min axis in (14) is calculated from (18). As
in the previous
case, the complete solution in 0ABC is given by formulas (9), (10) and (14),
complemented with the stress continuity condition (16) or (17).
m2 of
the directing unit vector of
stresses onto the
SH, min axis in (14) is calculated from (18). As
in the previous
case, the complete solution in 0ABC is given by formulas (9), (10) and (14),
complemented with the stress continuity condition (16) or (17).
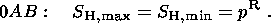
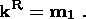
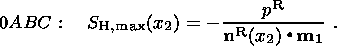
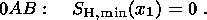
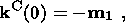
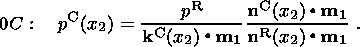

 D
D D in Figures 1 and
2) is plotted in Figure 3. After
Gölke and Coblenz [1996],
I set the modulus of the stress vector on the boundary 0A to be
pR = 25 MPa. This
value is based on model push estimates (e.g. see
[Parsons and Richter, 1980]).
D in Figures 1 and
2) is plotted in Figure 3. After
Gölke and Coblenz [1996],
I set the modulus of the stress vector on the boundary 0A to be
pR = 25 MPa. This
value is based on model push estimates (e.g. see
[Parsons and Richter, 1980]).

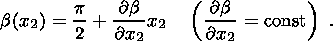
 b/
b/ x2 is
negative (positive), the collision force vector
tC rotates clockwise
(counterclockwise), as a point on 0C moves from 0 to
C (Figures 4a,
4c).
The
case
x2 is
negative (positive), the collision force vector
tC rotates clockwise
(counterclockwise), as a point on 0C moves from 0 to
C (Figures 4a,
4c).
The
case
 b/
b/ x2 = 0 means that the vector
tC is directed along the axis of the
maximum compressive stress
SH, max everywhere on 0C.
x2 = 0 means that the vector
tC is directed along the axis of the
maximum compressive stress
SH, max everywhere on 0C. 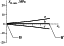
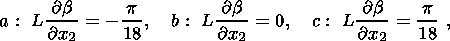
 C of the southern
boundary (Figure 2)
calculated from (24) is plotted
as a function of
x2 in Figure 4d. The difference between the functions
pC(x2) calculated at different values of the
gradient
C of the southern
boundary (Figure 2)
calculated from (24) is plotted
as a function of
x2 in Figure 4d. The difference between the functions
pC(x2) calculated at different values of the
gradient
 b/
b/ x2 from (26) is too small to be
reflected in Figure 4d. By contrast the stress
SH, min is much more sensitive to
small variations in
x2 from (26) is too small to be
reflected in Figure 4d. By contrast the stress
SH, min is much more sensitive to
small variations in
 b/
b/ x2 around zero. Figure 5 plots WESP values of the function
SH, min(x1) calculated from (14)
for three
x2 around zero. Figure 5 plots WESP values of the function
SH, min(x1) calculated from (14)
for three
 b/
b/ x2 values (26). Negative values of
x2 values (26). Negative values of
 b/
b/ x2 result in positive stresses
SH, min, whereas positive values of
x2 result in positive stresses
SH, min, whereas positive values of
 b/
b/ x2 give rise
to tensile stresses in the WESP region ( SH, min<0 ). The absolute value of
SH, min increases in the SE direction. If the collision
forces coincide in direction
with
SH, max (case (b) in (26)), a uniaxial compression
state ( SH, min = 0 )
independent of the
pC value arises in WESP, as well as in the entire region
0
ABC
x2 give rise
to tensile stresses in the WESP region ( SH, min<0 ). The absolute value of
SH, min increases in the SE direction. If the collision
forces coincide in direction
with
SH, max (case (b) in (26)), a uniaxial compression
state ( SH, min = 0 )
independent of the
pC value arises in WESP, as well as in the entire region
0
ABC

 b/
b/ x2, respectively.
x2, respectively.

 D
D D in Figures 1 and 2) fields of the maximum
shear stress
tmax(x1, x2)
= (SH, max - SH, min)/2
for three
D in Figures 1 and 2) fields of the maximum
shear stress
tmax(x1, x2)
= (SH, max - SH, min)/2
for three
 b/
b/ x2 value (26).
x2 value (26).

 b/
b/ x2<-p/9L.
x2<-p/9L.

 100 km. This is mainly due to
the fact that
the boundary stresses
pR refer to exactly this thickness of lithosphere.
Because of the averaging of stresses, the inferred model solution cannot be
directly compared with the observed depth variations of stress magnitudes and
stress regime types. However, the comparison between lateral variations in the
model stress field and experimental data leads to quite definite conclusions
about the collision force orientation pattern and magnitudes of the related
tectonic stresses. Instrumental measurements of near-surface stresses indicate
that the magnitude of the minimum horizontal stress in the northern and central
WESP parts is often close to zero or negative (on the order of
- 1 to
- 3 MPa)
[Becker and Davenport, 2001;
Froidevaux et al., 1980].
These results indicate
the tectonic stress
SH, min to be tensile, and therefore the solution
presented
in Figure 6c
is most consistent with experimental data. It is likewise consistent
with data on the spatial pattern of the stress regime, according to which the
strike-slip faulting regime prevails in the WESP territory (see Section 1.2).
The solution shown in Figure 6a complies with a compression regime in the WESP
region. Note also that a decrease in
SH, max in the NE direction and a decrease
in the negative value of
SH, min in the SE direction make the stress regime
close
to a tensile one in the northern Apennines region. Focal mechanisms of
earthquakes in this region provide the most reliable evidence of an extension
regime here (see Section 1.2). The model values of the maximum shear stress
tmax in this
region also reach a local extremum (Figure 7c). Thus, experimental
data on the magnitude and regime of stresses indicate that the direction of the
collision stresses
tC is close to that of
SH, max and rotates counterclockwise
when moving along the southern boundary in the eastward direction (Figure 4c).
100 km. This is mainly due to
the fact that
the boundary stresses
pR refer to exactly this thickness of lithosphere.
Because of the averaging of stresses, the inferred model solution cannot be
directly compared with the observed depth variations of stress magnitudes and
stress regime types. However, the comparison between lateral variations in the
model stress field and experimental data leads to quite definite conclusions
about the collision force orientation pattern and magnitudes of the related
tectonic stresses. Instrumental measurements of near-surface stresses indicate
that the magnitude of the minimum horizontal stress in the northern and central
WESP parts is often close to zero or negative (on the order of
- 1 to
- 3 MPa)
[Becker and Davenport, 2001;
Froidevaux et al., 1980].
These results indicate
the tectonic stress
SH, min to be tensile, and therefore the solution
presented
in Figure 6c
is most consistent with experimental data. It is likewise consistent
with data on the spatial pattern of the stress regime, according to which the
strike-slip faulting regime prevails in the WESP territory (see Section 1.2).
The solution shown in Figure 6a complies with a compression regime in the WESP
region. Note also that a decrease in
SH, max in the NE direction and a decrease
in the negative value of
SH, min in the SE direction make the stress regime
close
to a tensile one in the northern Apennines region. Focal mechanisms of
earthquakes in this region provide the most reliable evidence of an extension
regime here (see Section 1.2). The model values of the maximum shear stress
tmax in this
region also reach a local extremum (Figure 7c). Thus, experimental
data on the magnitude and regime of stresses indicate that the direction of the
collision stresses
tC is close to that of
SH, max and rotates counterclockwise
when moving along the southern boundary in the eastward direction (Figure 4c).
 10-2 MPa)
[Richardson, 1992].
When solving mathematical modeling problems of intraplate stresses,
the force
Tb is either neglected
(e.g. see [Gölke and Coblenz, 1996]) or its value and
direction are found from mechanical balance of forces applied to the plate under
the simplifying assumption of invariability of the stress
tb along the
base of lithosphere
[Cloetingh and Wortel, 1985;
Coblentz et al., 1998].
10-2 MPa)
[Richardson, 1992].
When solving mathematical modeling problems of intraplate stresses,
the force
Tb is either neglected
(e.g. see [Gölke and Coblenz, 1996]) or its value and
direction are found from mechanical balance of forces applied to the plate under
the simplifying assumption of invariability of the stress
tb along the
base of lithosphere
[Cloetingh and Wortel, 1985;
Coblentz et al., 1998].