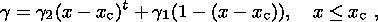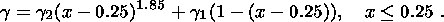Russian Journal of Earth
Sciences
Vol. 3, No. 4,
October 2001
Temperature benchmarks in the lithosphere,
marking the phase transformations of the matter, and the
possibilities of estimating their depths
V.
S. Yakupov and S. V. Yakupov
Mining
Research Institute for the Northern Territories, Siberian
Division, Russian Academy of Sciences, Yakutsk
Contents
Abstract
Extensive research into
temperature distribution in the lithosphere and upper mantle
revealed it to be highly ambiguous. Of great interest in this
context is the distribution of temperature benchmarks in the
lithosphere, which mark phase transitions in the individual
components of rocks and in the fluids filling their pores. As
follows from the percolation theory, the physical properties of
the rocks change jumpwise at the discontinuities produced by
their phase transformations. This simplifies the interpretation
of magnetotelluric and other electrical measurements, enhances
the reliability of its results, and facilitates the use of
radiolocation, especially in the case of relatively shallow
discontinuities. The discontinuities may not coincide in terms of
percolation and mechanical conpling, this explaining differences
in the results of electrical and seismic measurements.
There is extensive literature on the thermal state of the
deep-seated rocks of the Earth, including the papers reporting
activities in the frameworks of important international projects.
The ideas of temperature variation with depth, evaluated by some
geoscientists as highly ambiguous [e.g., Lyubimova and
Feldman, 1975], are based on the general
physical concepts and indirect data. The common approach is to
solve a thermal conductivity problem for a model of the crust and
upper mantle, which is believed by a particular researcher to be
most probable with various assumptions. A discrepancy between the
calculations based on different models of the lithosphere
averages 100% (of the least). Another approach is to use the
variation of the electrical conductivity of rocks with depth,
provided by the MTS, MVS, and other methods of electromagnetic
sounding with the controlled sources of an electromagnetic field
and compare it with the results of the experimental measurements
of the variation of electrical conductivity with temperature and
pressure. The most comprehensively developed models of a normal
(standard) resistivity section, based on MTS data [Van'yan and
Shilovskii, 1983; Zhamaletdinov,
1990], suggest a gradual growth of the
electrical conductivity of rocks with depth with the mere
variations of its gradient at the internal boundaries of the
section. In this case, too, the order of conductivity uncertainty
is great enough to produce differences between the models of
different authors, amounting to one or two orders of magnitude.
Another potential feasibility of estimating the temperature
distribution in the Earth's crust is to use geophysical methods
for locating temperature benchmarks - the boundaries at which a
phase transition, accompanied by a change of some physical
property of rocks, takes place, as some of the rock components or
the interstitial solution (generally fluid) attains a
phase-change temperature. Examples of these temperature
benchmarks are the transformation of water to ice or to some
supercritical state, the partial melting of rocks (basalt) in the
asthenosphere, the transformation of ferromagnetic substances to
paramagnetics as the temperature attains the Curie point, the
transition of olivine to spinel, etc. The difficulty is that, for
example, the temperatures of water transition to ice, or to a
supercritical state [Smith, 1968],
depend on the composition and concentration of substances,
dissolved in it, and on pressure. Uncertainty of the same kind is
encountered, for a number of reasons, in the cases of a partial
melting zone in the asthenosphere and in the zone of olivine
transition to spinel. In accordance with the hypothesis of the
pyrolite composition of the Earth's mantle, and with the
assumption of Fe/(Fe + Mg) 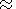 0.1, the temperature of this phase transition under pressure of
135 kb must be 1600o
0.1, the temperature of this phase transition under pressure of
135 kb must be 1600o 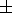 50o C [Zharkov, 1978]. This temperature will be different in the
case of any deviations of the olivine composition from the
composition mentioned above. Akimoto and Fujisava [1965] found the temperature of the phase
transition of olivine to spinel at 43.8 kb to be
~1170o C. It follows that in the general case we are
dealing with the temperature estimation of a particular phase
transition from above or from below. Another important condition
is the character of a change in the studied property of the rock
during its phase transition: jumpwise, as follows from the
general phase transformation theory, or the variation gradient of
a given property changes with depth, as it is assumed for the
upper boundary of the asthenosphere [Van'yan and
Shilovskii, 1983].
50o C [Zharkov, 1978]. This temperature will be different in the
case of any deviations of the olivine composition from the
composition mentioned above. Akimoto and Fujisava [1965] found the temperature of the phase
transition of olivine to spinel at 43.8 kb to be
~1170o C. It follows that in the general case we are
dealing with the temperature estimation of a particular phase
transition from above or from below. Another important condition
is the character of a change in the studied property of the rock
during its phase transition: jumpwise, as follows from the
general phase transformation theory, or the variation gradient of
a given property changes with depth, as it is assumed for the
upper boundary of the asthenosphere [Van'yan and
Shilovskii, 1983].
The most
widely used temperature benchmark is the zero isotherm based on
the thickness of frozen rocks [Kalinin and Yakupov, 1989; Yakupov, 2000] and the isotherm of the Curie point of
magnetite based on the depth of the bottoms of the magnetized
bodies [Bulina, 1970; Volk et
al., 1977a, 1977b]. A
contact between thawed and frozen rocks is generally marked by
the abrupt changes of electrical conductivity, dielectric
constant, and, in the case of coarse-grained loose deposits and
coarse-clastic hard rocks, of seismic velocity, or, in the
general case, of electrical and acoustic impedances. The regions
with fresh and salt subpermafrost water can be distinguished by
the absence or presence of a stochastic correlation between the
thickness of the permafrost rocks and the conductivity of a
subpermafrost layer [Kalinin and Yakupov, 1989]. Therefore, in the regions of the
coexistence of frozen rocks and fresh subpermafrost water, the
position of the first of the above mentioned temperature
benchmarks - t = 0o C - can be located
reliably by the methods of electrical prospecting under favorable
conditions with a mean relative error of ~10%. We succeeded to
solve this problem for one of the largest water-bearing
structures with salt subpermafrost water, the Olenek artesian
water basin. We derived a temperature regression equation for the
lower contact of the frozen rocks as a function of their
thickness [Kalinin and Yakupov, 1989].

|
| Figure 1 |
Another difficulty is the fact that the
character of the variation of a particular physical property of
the rocks during their phase transformation is not clear at first
glance. One can assume the following variants for the behavior of
electrical resistivity with depth in the vicinity of or at the
boundary produced by a phase transition in any constituent of the
rock (Figure 1). The
simplest case
(Figure 1a)
is, for example, a change of resistivity at the lower boundary of a lithologically
homogeneous frozen rock sequence with subpermafrost fresh water, that is, at a zero
temperature
[Yakupov, 2000],
or a change of the magnetic permeability of ferromagnetics at a Curie
temperature. The electrical conductivity of rocks increases at depth with a temperature
growth. It is
believed that with the formation of a partial melting zone in the asthenosphere,
its conductivity
grows with depth more rapidly, so that its upper surface is marked by an abrupt (jumpwise)
growth
of a conductivity gradient
[Van'yan and Shilovskii, 1983],
this being the most complex case (Figure 1d). In view of its generality, we will consider
this case
using the theory of phase transitions and the idea of a percolation theory. A zone
of partial melting arises in the top of the asthenosphere
because of basalt melting. The melt portion (2 to 30% of the volume after Ringwood
[1975])
is believed to grow with temperature, that is, with depth. It is known, however,
that with all other
factors being equal, any phase transition of a particular material from one state
to another takes
place at a constant temperature. In the case of a high heat flow, that is, in the
case of fairly rapid
heating or cooling, a transition zone can arise, where both a solid and a liquid
phase coexist.
Excluding the cases of the origin of magma chambers in the regions of volcanic activity,
this
phenomenon does not take place in the deep lithosphere, and the thermal state of
the latter can be
taken to be quasistationary. Therefore a partial melting zone in the asthenosphere
is bound to have
a distinct interface, where some of its physical properties change jumpwise. This
interface shows
pressure and temperature variations, and hence changes in resistivity, but not in
the melt content, at
least in the case of a two-component material.
It is of interest to consider electrical resistivity at the boundary of a partial
melting zone and
in both of its sides in terms of a percolation theory. The rocks of the lower lithosphere
and
asthenosphere are polycrystalline formations. The arrangement of individual components
in them is
the compact packing of their chaotically distributed particles of different size
and form. In this case
the electrical conductivity of such a fairly large 3-D system can be described by
the formula
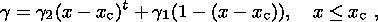 | (1) |
where
g1 is the conductivity of the asthenosphere
above the partial melting zone,
g2 is the
conductivity of the melt,
x is the relative melt content from 0 to 1,
x c is the melt critical value, at
which melt percolation takes place, this value being 0.25 in our case, and
t is the critical index of
electrical conductivity. Formula (1) is valid, as a first approximation, with an
accuracy of a factor
for
g1 and
g2 (we are interested in the behavior
of the electrical conductivity of rocks in the
vicinity of or at the melt percolation). Taking into account the sinuosity of the
framework of an
infinite melt cluster, proved for 3-D media,
t = 1 + n, where
n is the index of the correlation
radius, equal to 0.8-0.9. It should be added that the formation of an infinite cluster
is marked by
g tending to be equal to
g1. Hence, we arrive at
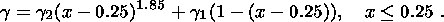 | (2) |
|
|
Figure 2
|
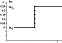
Figure 2 shows a logarithmic curve of the variation of the systems'
electric conductivity as a
function of temperature, where the dots show the
logg = f(x) values in accordance
with formula
(2). It should be emphasized that electric conductivity varies further with depth,
following pressure
and temperature variations: the melt portion in the resulting
two-phase system remains constant and
can change (jumpwise!) only when another component of the asthenospheric material
begins to
melt. To sum up, the interfaces produced by the phase changes of the material, when
the
percolation threshold is achieved, are marked by the jumpwise changes of at least
some of the
physical properties of the material, and by the
g = j(z)
function having the form displayed in
Figure 1c,
in the case of electric conductivity. This distribution of the electric conductivity
of
lithospheric rocks with depth simplifies the interpretation of magnetotelluric and
magnetic variation
measurements and also of the measurements made using the controlled sources of the
electromagnetic field. Moreover, this facilitates the use of radiolocation where
the appropriate
equipment is available. The main trends of research here are the use of high-power
MHD
generators [Velikhov and Volkov, 1982] to generate pulsed
electromagnetic fields; the use of the strength of the magnetic field as
the parameter of interest, and the use of high-precision magnetometers based on the
Josephson
effect as receivers to record the arrival times of reflected waves. This will enhance
highly the accuracy of determining the
depths of the discontinuities in question.

|
|
Figure 3
|
The main contribution to error in plotting the temperature
t variation with depth
t = f(z) will be made by the determination of the temperature
of a particular
phase transition, which depends on the contents of other rock
components and pressure. This
temperature is known for the freezing of fresh water in the pores of the rocks and
for the
second-order phase transitions accompanied by the transformation of ferromagnetic
minerals to
paramagnetic ones, magnetite and pyrrhotite. Other cases will deal with the estimation
of the
phase-transition temperature from below or from above depending
on the contents of volatiles and other
components in the rocks. All of these estimates will be refined with time. The hypothetic
function
t = f(z) will have the form similar to that shown in Figure 3, on the
assumption that all interfaces
produced by the phase transitions of the material were located in one region or under
similar
conditions. The dotted lines in Figure 3 show the positions of the interfaces with
the known phase
transition temperatures (water - ice; pyrrhotite, magnetite – paramagnetics). The
horizontal line
segments in Figure 3
are conventionally equal to the range of the potential temperature variation for
a
particular phase transition: of water to its above-critical state, of olivine to
spinel, of basalt melting;
the dashed lines depict the
t = f(z) estimates from below, the
dotted lines, from above. In the
general case, after the formation of melt from one of the rock components, its segregation
and
changes in the contents of or in the ratio between some other rock components, e.g.
water, or in
pressure, may involve the melting of another rock component, then of another, and
so on. Each
time during a next phase transition in the rock components (meaning their melting),
the total
volume of the melt will increase jumpwise, while the temperature of the rock as a
whole will remain
constant till the end of the next phase transition. Melt percolation may take place
at one of these
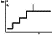
|
|
Figure 4
|
phase transitions, and not necessarily at the first one, as depicted conventionally
in Figure 4.
The
lower boundary of the partial melt zone will obviously be controlled by the depletion
of the
relatively low-melting components of the asthenospheric substance.
The threshold of percolation, as a constant of transportation processes, and the
threshold of
mechanical coherence in the system arising as a result of a phase transition may
not coincide, and in
this case the positions of the interfaces determined by electrometric and seismometric
methods will
be different (see, for example,
[Yakupov, 2000]).
Where the content of a new phase is small, the
mechanical coherence of the initial rock remains intact, as does its homogeneity
in terms of the
related parameters.
Conclusion
1. The positions of the interfaces produced in the lithosphere by phase transitions
in the
individual components of the rocks, or in their interstitial fluids, control the
positions of its
temperature benchmarks. The temperatures of some phase transitions are known. In
the case of the
others it is controlled by the ratio or contents of the other rock components and
pressure.
2. Some of the physical properties change jumpwise at
the interfaces produced by the
above mentioned phase transitions. Three models are proposed for their distribution
in depth:
models a, b, and c in Figure 1. These models can be used to determine the positions
of these
interfaces, in the case of their sufficient contrasts, using magnetotelluric sounding,
magnetic
variation measurements, and soundings using controlled field sources. This simplifies
the
interpretation of the results and makes them more reliable. Theoretically, this problem
can be solved
using radiolocation. Some technical means, though limited in their performance, are
available.
3. Where the content of a new phase is sufficient, the interfaces may coincide
in terms of
percolation and mechanical coherence, and in this case its position can be located
by electrometric
and seismic methods. Where these thresholds differ, but have been achieved, the positions
of the
interfaces indicated by electrometry and seismic methods are different: the interface
determined by
electrometry must lie higher. Where the threshold of mechanical coherence is not
attained, the
physical properties of rocks remain intact.
4. The materialization of the ideas advanced in this
paper will hopefully enhance our
knowledge of the temperature distribution in the lithosphere, for instance, in the
form presented in
Figure 3.
References
Akimoto, S., and Y. Fujisawa, Demonstration of electrical conductivity produced by
an
olivine-spinel transition, J. Geophys. Res., 70, (2), 443-450, 1965.
Bogorodskii, B., Ch. Bentley, and P. Gumandson, Radio Glaciology, 312 pp.,
Hydrometeoizdat, Leningrad, 1983.
Bulina, L. V., The use of airborne magnetic data for the study of the deep crustal
structure
of the Siberian craton, Sov. Geologiya, (5), 134-138, 1961.
Bulina, L. V., Patterns of the spatial distribution of the bottoms of magnetized
bodies in the
Earth's consolidated crust, Izv. Akad. Nauk SSSR, Ser. Geol., (5), 40-47,
1970.
Kalinin, V. M., and V. S. Yakupov, Regional Patterns in the Behavior of Permafrost
Rocks,
142 pp., Yakutsk, 1989.
Lyubimova, E. A., and I. S. Feldman, The heat flow, temperature and electric conductivity
of the Earth's crust and upper mantle, in The Earth's Crust and Upper Mantle,
pp. 144-190,
Moscow, 1975.
Petrova, G. N., D. M. Pecherskii, and A. V. Lykov, Magnetic minerals and
magnetic
anomalies, in Magnetic Anomalies of the Earth, pp. 55-63, Naukova Dumka,
Kiev, 1976.
Ringwood, A. E., Composition and Petrology of the Earth's Mantle, McGraw-Hill,
New
York, 1975.
Smith, F. G., Physical Geochemistry, 475 pp., (Russian translation),
Nedra, Moscow, 1968.
Strakhov, V. N., and M. I. Lapina, Inverse magnetic problem: Umbiguity of solution,
in
Magnetic Anomalies of the Deep Earth, pp. 185-199, Naukova Dumka, Kiev,
1976.
Van'yan, L. L., and P. P. Shilovskii, Electric Conductivity of Rocks in the Deep
Crust of the Oceans and Continents, Nauka, Moscow, 1983.
Velikhov, E. P., and Yu. M. Volkov, Prospects of using MHD generators in geology
and
geophysics, in The Use of Impulse MHD Generators in Deep Electromagnetic Sounding,
pp. 5-25,
Apatity, 1982.
Volk, V. E., V. A. Osipov, and V. N. Shimaraev, The use of magnetic data
in the study of
the Earth's crust under the USSR Arctic shelf, in The Crustal Structure of Continents
and Oceans, LOE Transections, iss. 2, pp. 93-99, Leningrad, 1977a.
Volk, V. E., G. I. Gaponenko, E. N. Zatsepin, et al., The study of the
Earth's crust below
the shelf of the Arctic and Far-East seas of the USSR using airborne magnetic data,
in Problems of Geophysical Investigations in the Polar Regions of the Earth,
pp. 53-67, NIIGP, Leningrad, 1977b.
Yakupov, V. S., Permafrost Investigation by Geophysical Methods, 316 pp.,
Yakutian Branch, Ross. Akad. Nauk Publ. House, Yakutsk, 2000.
Zhamaletdinov, A. A., Electric Conductivity of the Lithosphere: A Model Based
on Controlled Field Source Measurements, 159 pp., Nauka, Leningrad, 1990.
Zharkov, V. N., Internal Structure of the Earth and Planets, 191 pp.,
Nauka, leningrad, 1978.
Zhdanov, M. S., Electrical Prospecting, 316 pp., Nedra, Noscow, 1986.
Load files for printing and local use.
This document was generated by TeXWeb
(Win32, v.1.3) on November 10, 2000.
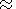 0.1, the temperature of this phase transition under pressure of
135 kb must be 1600o
0.1, the temperature of this phase transition under pressure of
135 kb must be 1600o 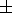 50o C [Zharkov, 1978]. This temperature will be different in the
case of any deviations of the olivine composition from the
composition mentioned above. Akimoto and Fujisava [1965] found the temperature of the phase
transition of olivine to spinel at 43.8 kb to be
~1170o C. It follows that in the general case we are
dealing with the temperature estimation of a particular phase
transition from above or from below. Another important condition
is the character of a change in the studied property of the rock
during its phase transition: jumpwise, as follows from the
general phase transformation theory, or the variation gradient of
a given property changes with depth, as it is assumed for the
upper boundary of the asthenosphere [Van'yan and
Shilovskii, 1983].
50o C [Zharkov, 1978]. This temperature will be different in the
case of any deviations of the olivine composition from the
composition mentioned above. Akimoto and Fujisava [1965] found the temperature of the phase
transition of olivine to spinel at 43.8 kb to be
~1170o C. It follows that in the general case we are
dealing with the temperature estimation of a particular phase
transition from above or from below. Another important condition
is the character of a change in the studied property of the rock
during its phase transition: jumpwise, as follows from the
general phase transformation theory, or the variation gradient of
a given property changes with depth, as it is assumed for the
upper boundary of the asthenosphere [Van'yan and
Shilovskii, 1983].