Modeling of seismo-electromagnetic phenomena
N. Gershenzon and G. Bambakidis
6. Discussion and Conclusions
A. Major seismo-electromagnetic phenomena can be described by the following
model. The final phase of
the pre-earthquake process is accompanied by the formation of multiple cracks. Cracks
appear not only in
the focal area but also in a neighborhood. This occurs because regional geodynamic
processes are connected
by the global shear stress. The appearance of a crack creates, in its neighborhood,
a mechanical disturbance
over a broad frequency range. In general, the spectral density of the disturbance
consists of two parts: a
zero-frequency spike related to a change in the residual strain, and a broad region
from zero up to the MHz
range, related to an impulse-like process. In a crust saturated with water (the usual
case), a crack will also
cause a change in the pore water pressure, and the spectral density of this response
is much less broad,
extending from zero up to the range of kHz. Localized mechanical or pore pressure
changes give rise to
electromagnetic emission by a variety of mechano-electromagnetic transducer mechanisms.
The emission
will have a spectral density which spans the same range as its source.
B. The major known mechano-electromagnetic mechanisms
which may be applied to the earth's crust,
namely piezomagnetic, piezoelectric, electrokinetic and induction, have been considered
and are
compared in Table 1. From this table one can see that a piezomagnetic source
has strength comparable to
that of a pure quartz piezoelectric source. In the case of high conductivity in
the earth's crust, the strength
of an electrokinetic source and a piezomagnetic source are also comparable. The
magnitude of the
induction effect is usually very small compared to the other three, but it could
be comparable to them for a
source of size 1 km or more.
C. Since the dimensions of the EM source are, in most real cases, much smaller
than the distance from
source to detector, all sources are represented by a magnetic or electric dipole.
Formulas 21 and 22 and
Table 2
express the magnitude of the electric and magnetic dipoles in terms of the parameters
of both the
earth's crust and the mechanical disturbances. The mechanical parameters important
in calculations, namely
strain spectral densities
e(w, r)
and
q(w, r),
pore water pressure spectral
density
P (w, r), crack density
n, and average shear and volume strain changes
e and
q, are given in equations 1c, 3a, 4, 5 and
5a. The relation between volume strain and pore water pressure is
given by equation A9.
Expressions 18(a-d) can be used for calculating the magnetic and electric fields
in the so-called static zone
and expressions B1-B32 in the near, intermediate and far zones for
s/we>1.
When
s/we<1,
expressions 19(a-d) and 20(a-d) can be used in the
near and far zones, respectively. In order to connect the "detected''
(filtered and averaged) EM field to the real field one uses expressions 26, 28 and
27, 29.
Collectively, all the above formulas represent the necessary relationships for estimating
the measured EM
field, at the detector, for a wide range of frequencies and at various distances
from the source. Through
them, the physical parameters of both the earth's crust and of a localized disturbance
are connected to the
measured EM field.
D. The magnitude and morphological features of major SEM phenomena have been
interpreted on the basis
of the model developed here.
1. Tectonomagnetic anomalies can be described either by the piezomagnetic or
electrokinetic effect. In
rocks containing titano-magnetite, residual strain as a result of the cumulative
action of crack formation in a
localized area can produce magnetic field variations of the order of nT. The same
order of magnetic
variation can be produced in water-saturated rocks of high electrical conductivity
(s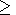 10-2/W-m) by changes in pore water pressure. These
two mechanisms can be distinguished by the temporal behavior of the
magnetic variation (step-function behavior corresponding to the piezomagnetic mechanism
and unipolar
behavior corresponding to the electrokinetic mechanism).
10-2/W-m) by changes in pore water pressure. These
two mechanisms can be distinguished by the temporal behavior of the
magnetic variation (step-function behavior corresponding to the piezomagnetic mechanism
and unipolar
behavior corresponding to the electrokinetic mechanism).
2. Of the mechanisms considered in this paper, only the electrokinetic mechanism
can explain the main
features of electrotelluric field anomalies, namely duration, magnitude, and high
degree of selectivity.
3. Geomagnetic variation in the ULF range may be explained on the basis of the
electrokinetic effect,
when the detector is located about a water-saturated layer which has a comparatively
high conductivity.
While the piezomagnetic effect could also contribute to the variation, the electrokinetic
effect is a more
likely mechanism. The main reason for this is the difference in the spectral density
of the mechanical
disturbances associated with each. The energy of a piezomagnetic source is distributed
widely from zero up
to radio frequencies. The electrokinetic source is usually much narrower, with correspondingly
much more
energy in the ULF range.
4. The most powerful source of EME in the RF range is the piezoelectric effect
due to the presence of
quartz grains in the crust. The magnitude of the piezomagnetic effect in the RF
range is 2-3 orders of
magnitude less.
E. Calculations based on the model presented here show that the source of all
types of EM anomalies
considered here should be local, i.e. close to the detector but not necessarily
in the focal region, in order to
be observed. The maximum distance from source to detector depends on the type of
anomaly and on the
detector, and can range from several hundred meters to several kilometers. One of
the best experimental
confirmations of this statement is the fact that there are no SEMS during earthquakes
(excluding co-seismic
signals accompanying seismic waves). An earthquake itself is a huge mechanical disturbance,
much bigger
than the disturbances we expect during the pre-seismic time. So it should, and probably
does, produce large
SEMS from all the mechanisms we have discussed. But the magnitude of these signals
decreases as an
inverse power of the distance and at 10 km or more from the focal region it
should be negligible in most
cases. That is why "global'' models, which suppose that the source of SEM anomalies
is at the earthquake
origin, have to introduce some additional (and sometimes unrealistic) suppositions
to explain how the signal
can still be detected at several hundred kilometers from the focus. Even with these
suppositions, the
experimental fact is that no SEMS are observed during a quake.
F. Some general recommendations for field experiments can be made based on the
model described here.
Since all sources should be close to the detector to be observed, the placement of
detectors is critical and
depends on the frequency range and on whether an electric or magnetic measurement
will be made. For
example, the nearby presence of rock containing titano-magnetite is required for
monitoring tectono-magnetic
variation. The existence of a nearby water-saturated layer provides a necessary condition
for
electrotelluric anomalies as well as geomagnetic variation in the ULF and quasi-static
ranges. The best
condition for the appearance of anomalies in the RF range is the nearby presence
of quartzite or granitic rock
and, for their detection, a low crustal conductivity about the detector is also necessary.
Because all sources
become active only under a mechanical disturbance, the presence of an active geophysical
structure such as a
fault is necessary.
Since magnetic variation from an electrokinetic source can apear only in the presence
of a vertical
inhomogeneity, the detector should be placed close to it. For monitoring an electrotelluric
anomaly the best
setting of the electrodes is across the vertical plane defining the inhomogeneity.
The anomaly is enhanced if
the water table is close to the surface, provided the electrode separation is not
much less than the depth of the
table. An electrotelluric anomaly can also be observed without a vertical inhomogeneity
if the electrodes are
displaced vertically, with one above the water table and the other below it.
Since ULF and RF anomalies are expected to have a pulse-like character, “impulse
averaging” is
the best technique for monitoring them. This technique avoids the “dead time” between
impulses, and
requires a small acquisition time. On the other hand, the acquisition time should
be large enough to record
the entire impulse (or a cluster of multiple impulses). The choice of optimal threshold
value is also
important for this type of averaging, since it should be low enough to record small
impulses but high enough
for a good signal-to-noise ratio. Following the above recommendations would involve
investigating, at the
detector location, both the composition of the crust and the noise level in the frequency
range of interest.
G. Since our results indicate that SEMS arise from a local source, the usual
triangulation technique cannot be
used to locate a distant seismic focus. At the heart of our model, however, earthquakes
and SEMS are
connected by a global stress field. This connectedness means that the possibility
still exists for locating a
seismic focus using SES. One way is by statistical analysis of these two types of
events (SES and
earthquakes) using a detector network
[Varotsos et al., 1996a, 1996b].
Such an analysis may allow one to establish a connection between a group of SES measurement
points and a group of seismic areas.
H. EM emission is a secondary effect of local changes in the stress field of
the crust. The question arises,
why not measure the stress changes directly? After all, it is known that the latter
can be measured with more
accuracy. There is at least a twofold answer to why measurements of EME can be useful
and can give
additional (and sometimes the only) information about stress changes. First, EME
measurements can give
information about remote stress field changes, while direct stress field measurement
give information only at
the immediate vicinity of the detector. Second, the latter type of measurement is
usually more expensive than
EME detection.
Acknowledgments
The authors would like to thank their colleagues Paul J. Wolfe, Kostas Eftaxias
and Nikos Bogris
for several helpful conversations. Special thanks go to Ms. Barbara O'Brien for typing
the manuscript. This
research was supported in part by NATO Grant CRG970028.
This document was generated by TeXWeb
(Win32, v.1.3) on October 28, 2000.
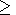 10-2/W-m) by changes in pore water pressure. These
two mechanisms can be distinguished by the temporal behavior of the
magnetic variation (step-function behavior corresponding to the piezomagnetic mechanism
and unipolar
behavior corresponding to the electrokinetic mechanism).
10-2/W-m) by changes in pore water pressure. These
two mechanisms can be distinguished by the temporal behavior of the
magnetic variation (step-function behavior corresponding to the piezomagnetic mechanism
and unipolar
behavior corresponding to the electrokinetic mechanism).