
During the past century a wealth of SEM data has accumulated which has been interpreted as having some relation to pre-seismic processes. We want now to apply our model to the interpretation of some of this data. The search for SEM anomalies has spanned a wide frequency range from quasi-static (periods of weeks or months) up to radio frequencies ( < 50 MHz). Both magnetic and electric fields have been measured, using detectors below ground as well as above ground. A partial list of the types of anomaly which have been reported includes
We will estimate and compare with reported data the magnitude of the various types of SEM anomaly.
This type of field experiment has a very long history. Occurrences of very large anomalies were observed centuries ago [Rikitake, 1976a, 1976b]. These early effects were reported to be comparable in magnitude to the geomagnetic field. However, as Rikitake has jokingly commented, the magnitude of reported anomalies seems to have fallen off exponentially with time, so the present day anomalies are some four orders of magnitude smaller, i.e. of order 1-10 nanotesla (nT). The typical duration time, T, varies from days to month, but there have been reports of T as small as minutes [Johnston, 1989; Moore, 1964; Mueller and Johnston, 1998; Shapiro and Abdullabekov, 1982; Shapiro et al., 1994; Skovorodkin et al., 1978]. In those cases where tectonomagnetic anomalies are followed by quakes, the elapsed time before the quake is comparable to T. Anomalies have been detected at distances up to 30 times the size of their origin. The general hypotheses put forth to explain these anomalies are based either on the piezomagnetic effect [Sasai, 1980, 1991; Stacey, 1964; Stacey and Johnston, 1972; Zlotnicki and Cornet, 1986] or the electrokinetic effect [Fitterman, 1978, 1979a; Mizutani and Ishido, 1976; Mizutani et al., 1976].
First, let's estimate the size of the anomalous magnetic field assuming it originates from piezo-magnetism. Suppose we have some region of the crust, of linear extent r, located at distance R from the point of measurement, and that this region has piezomagnetic properties. Suppose further that during the duration time T of the anomaly a number N of cracks form in this region, with N given approximately by (see equation 5)
 | (30) |
The residual strain field around an isolated crack extends out to about three times the crack length (see equation 1b). This leads to the appearance of a magnetic dipole, for the ith crack, of moment
 | (31) |
where ti is the time of appearance of the ith crack (measured from when the anomaly begins) and the components of M0 are given by equation 10. From equations 18a and 31 the cumulative effect is to create a magnetic field B whose magnitude is given approximately by
 |
For simplicity we assume that all cracks have the same length and orientation and have the same value of R. Then from equations 4, 10 and 30 the magnetic field, after all N cracks have formed, becomes approximately
 | (32) |
From this we see that the size of the magnetic anomaly is independent of crack size
but
proportional to the coefficient
a or the average shear strain
e,
and strongly dependent on the ratio ( r/R ). The latter dependence means
that
the anomaly is stronger when it arises in a region close to the observation
point. It also means that sources close to the observation point ( r/R 1 )
have a
higher probability of being observed compared to distant sources ( r/R ranging
from 1/10 to 1/30). We expect this statement to be valid
even when the density of cracks in nearby regions is low (small
a or
e )
compared, for example, to the high crack density near the focal point of a distant
quake. Estimating the strain
e to be 10
-4 to 10
-5 ,
setting
r/R=1, and using values of
ms, c||
and
I from Tables A1
and 1, equation 32 gives
B
1 )
have a
higher probability of being observed compared to distant sources ( r/R ranging
from 1/10 to 1/30). We expect this statement to be valid
even when the density of cracks in nearby regions is low (small
a or
e )
compared, for example, to the high crack density near the focal point of a distant
quake. Estimating the strain
e to be 10
-4 to 10
-5 ,
setting
r/R=1, and using values of
ms, c||
and
I from Tables A1
and 1, equation 32 gives
B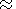 0.3-3 nT, which is comparable
to the observed data.
0.3-3 nT, which is comparable
to the observed data.
The model based on the electrokinetic effect was first proposed by Mizutani and Ishido [1976]. These authors noted the relation between local geomagnetic anomalies and the level of the water table during the Matsushiro earthquake swarm. Fitterman developed this model further [Fitterman, 1978, 1979a, 1981].
The magnetic field associated with a system of currents generated by an electrokinetic source has some characteristic features. It is known [Fitterman, 1978] that in any homogeneous medium with an arbitrary distribution of pressure variations due to pore water, the geomagnetic effect is zero. That is, the electric current due to the motion of the pore water is exactly cancelled by the current arising from the electric field which is created. A non-zero effect occurs only in an inhomogeneous medium, and its magnitude depends only on the degree of inhomogeneity. However, not all types of inhomogeneity will produce a geomagnetic effect on the earth's surface. For example, it can be shown that when the inhomogeneity is only in the vertical direction, i.e. in a horizontally stratified crust, there is no above-ground geomagnetic effect [Fitterman, 1978; Gershenzon, 1992]. But there will be an effect below the surface, and it will be greatest at the boundary between strata. So geomagnetic effects of an electrokinetic nature arising from geodynamic processes would be observed on the earth's surface only if there were inhomogeneities in the horizontal direction (e.g. faults or inclusions).
For the estimation of the magnitude of magnetic field disturbances, therefore, it makes sense to consider, as the simplest model, two media (medium 1 and medium 2) separated by a vertical boundary. In this case the magnitude of the magnetic field disturbance at the intersection of the boundary with the surface can be estimated by the simple formula [Fitterman, 1979a, 1979b]
 | (33) |
where f is a dimensionless geometrical factor weakly dependent on the size of the boundary. For realistic cases f does not exceed 20 [Gershenzon and Gokhberg, 1992]. We shall use f =10. The pressure variation P arises from the appearance of multiple cracks in some regions. Expressing P in terms of q , the change in the volume strain, via equation A9, we obtain B for various values of q, s1, s2 and C1-C2 (Table 4). This table shows that the magnetic disturbance becomes significant (~ 1 nT) only for changes in volume strain greater than 10-6 and conductivities greater than 10-2/W-m.
We have not considered changes in water permeability or changes in the streaming potential, C, accompanying a pre-seismic process. These changes could affect the size of the geomagnetic anomaly. Changes in C are difficult to calculate because they are related to changes in the composition of the pore water. Changes in water permeability likewise are difficult to calculate but might be significant when the porosity is small and q is large. The seasonal runoff of ground water in mountainous areas has been observed to give rise to a large electrokinetic current and magnetic field. For example, a pore pressure difference of 10 6 Pa over a horizontal distance DL of 100 m gives a pressure gradient dP/dx of 104 Pa/m, which results in a magnetic field B = CmsDLdP/dx ranging from 10 to 100 nT for s=10-1/W-m and C = 10-7 to 10-6 V/Pa. A change of 10% in this field due to a pre-seismic process would give rise to an easily observable anomaly of 1 to 10 nT.
So both mechanisms, under appropriate conditions, can produce fields strong enough to be comparable to observed anomalies. However we emphasize that one of these conditions is that the distance from the point of measurement to the source be comparable to the size of the source.
We also note that there is a simple way of distinguishing which of these two types of sources, piezomagnetic or electrokinetic, is responsible for an observed magnetic anomaly, based on the temporal behavior of the latter. If the anomaly behaves approximately like a step function, i.e. shows a residual field, then it is piezomagnetic in origin. If it behaves approximately as a unipolar pulse with no residual field, it is electrokinetic in origin.
The search for earthquake precursors in the electrotelluric field extends back about eighty years. This search has been conducted in many areas of high seismic activity worldwide (Japan [Fukutomi, 1934; Miyakoshi, 1986; Noto, 1933; Ozima et al., 1989; Shiratori, 1925; Uyeda, et al., 2000], the former Soviet Union [Sobolev et al., 1981], Greece [Lighthill, 1996; Varotsos and Alexopoulos, 1984a, 1984b, 1987; Varotsos et al., 1993], China [Qian et al., 1990; Raleigh et al., 1977], Bulgaria [Ralchovsky and Komarov, 1987], USA [Sornette and Sornette, 1990]). Several hundred cases have been reported which relate such anomalies to strong nearby quakes. In general, the morphological features of these anomalies are defined by the region of occurrence and method of detection. The magnitude of the disturbances ranges from a fraction of a millivolt to a few tens of millivolts; it depends on the quake magnitude and distance from the epicenter but in many cases the magnitude is independent of the measurement line length. The duration of an anomaly can range from minutes to weeks and is only weakly dependent on quake magnitude and distance from epicenter.
The nature of these anomalies is not well known. There exist models based on the classical and non-classical piezoelectric effects discussed in Section 3B [Gokhberg et al., 1985; Slifkin, 1996; Sobolev and Demin, 1980; Varotsos and Alexopoulos, 1986], and the electrokinetic effect (Section 3C) [Bernard, 1992; Dobrovolsky et al., 1989; Fitterman, 1979b; Gershenzon and Gokhberg, 1989, 1993]. Sometimes the occurrence of anomalies has been ascribed to changes in the conductivity of the crust [Meyer and Pirjola, 1986]. In some cases they have been explained in terms of changes in the chemical composition of pore water around one or both of the measurement electrodes, giving rise to an apparent electrotelluric signal [Miyakoshi, 1986]. Such chemical changes could alter the z -potential of the double electric layer at the electrode-water interface.
We ask how pre-seismic processes relate to the appearance of an electrotelluric field at distances of tens to hundreds of kilometers from the epicenter. There are at least two alternative explanations.
The first one, preferred by most experimenters, supposes that somehow a large current is generated in the focal area and is distributed over a great distance to the detector. This explanation has not been confirmed in most cases. For example, Yoshimatsu [1957] used two parallel lines 100 m and 1500 m in length and the signal appeared only in the shorter line, whereas we would expect it to appear in both lines if the above explanation were true. Noto [1933] used two lines perpendicular to each other and the anomalous signals appeared in only one of them, which is again difficult to explain in terms of a large-scale current distribution, even in the presence of inhomogeneities in the conductivity. Miyakoshi [1986] described anomalies as close as 3 km from the epicenter of a 5.2 magnitude quake. He used three short lines, each 30 m long, in a geophysical tunnel, and two perpendicular lines on the ground, each 600 m long. He saw anomalous signals only in one of the short lines. They clearly exceeded normal levels and lasted about two months. If these signals were electrotelluric in origin, they certainly could not be explained in terms of a large-scale current system. The so-called DV/L test has been introduced to eliminate noise for short lines on VAN and similar networks. But there are examples where this test does not work on such networks [Gershenzon and Gokhberg, 1993; Uyeda, et al., 2000].
In order to explain the appearance of SES generated by pre-seismic processes in the focal area but located hundreds of km from this area, Varotsos et al. [1998] proposed the existence of a special pencil-like region of high conductivity in the crust, extending from the dipole and terminating at the field point. Although regions of strong inhomogeneity are not unusual in the crust, we think the existence of this special pencil-like form extending for several hundreds of km and terminating very close to the detector is unrealistic. Calculations by Bernard [1992] also support this conclusion.
The inadequacy of the explanation in terms of a large-scale current system originating in the focal area leads us to the second alternative, namely, a large-scale mechanical stress field which can, under certain condition, produce electrotelluric anomalies locally. Then the morphological features of the anomalies represented by the several examples cited in the previous paragraph can be explained in terms of the electrokinetic effect [Bernard, 1992; Dobrovolsky et al., 1989; Gershenzon and Gokhberg, 1989, 1993]. As mentioned before, the current distribution created by an electrokinetic source in a homogeneous medium is zero on a scale larger than the individual grains. Non-zero currents will appear only on the boundary separating two homogeneous components of an inhomogeneous medium. Across this boundary, the electric potential will be discontinuous, and two electrodes placed on opposite sides of the boundary will show a voltage practically independent of the distance between the electrodes. This voltage will depend on the strength of the electrokinetic source and the electrical characteristics of the two components. This would explain why the anomalous signals are selective and why the strength of an anomalous signal is sometimes independent of the length of its measurement line.
The typical pore pressure relaxation time depends on the size and shape of the disturbed region and can range from minutes to hours, days or weeks, which coincides with the time range over which electrotelluric anomalies are observed to occur. No single mechano-electromagnetic mechanism involving the crystal matrix of the rocks, e.g. piezomagnetic or piezoelectric (classical and non-classical), could act over such large time scales, because the formation time for such disturbances is only 1 second or less, i.e. of the order of the linear extent l of the region divided by the elastic wave velocity. Once formed, such disturbances dissipate with a time constant msl2 which is even smaller.
Let's calculate the magnitude of the electrotelluric field from an electrokinetic source. The maximum effect occurs when the two electrodes span an inhomogeneity. In this case the potential difference Df can be expressed by
 | (34) |
In Table 5 we tabulate Df for a range of q and C1-C2.
Table 5 shows that strains exceeding the tidal value (10 -8 ) can be detected, but only under the following conditions:
In spite of the fact that no macroscopic electric current will exist in a homogeneous medium, an electric field can exist and is measurable. In a homogeneous medium the potential between points 1 and 2 is Df=C(P1-P2). Normally, if the electrodes are at the same depth the difference between P1 and P2, and hence Df, is negligibly small. But if the electrodes are at different depths (for example, one above and one below the water table) a significant potential can arise.
Consider a simple example. Suppose at t =0 a step-function change in volume strain (and resulting pore pressure) occurs in the vicinity of two electrodes placed in a homogeneous medium. If P1=P2 after the change, then Df remains zero. But if the environment around the two electrodes is slightly different, leading, for example, to different water permeabilities or different distances between the electrode and the water table level, the pressures P1 and P2 will relax back to their equilibrium values at different rates, leading to a spike in P1 and P2 at some time t>0. In such a case the duration of the anomaly does not depend on the source but on the local environmental differences between the electrodes. The theoretical shape of the spike coincides with the shape usually observed, in the SES reported by the VAN group. In addition, when several signals are observed their duration is usually the same, in agreement with this simple model.
The above example indicates that if, instead of offsetting the electrodes horizontally, they are offset vertically above and below the water table, the electrotelluric anomaly in a homogeneous medium might be maximized. In such an experiment it was shown that a good correlation existed between the electrotelluric field and tidal deformation [Gershenzon et al., 1990]. So under some conditions this method of measuring the electrotelluric field can be extremely sensitive. The use of a short vertical baseline also serves to reduce background noise. This method does have the disadvantage that it cannot detect an electrotelluric disturbance unless the electrodes are in a region where the volume strain is changing.
We have shown how placing the electrodes within a source
of mechanical disturbances can yield
detectable electrotelluric fields, even when the source is as weak as tidal deformation.
Now we consider the
situation where the electrodes are placed outside the source. For purposes of estimating
the effect we use
equation 18b, which gives the electric field associated with a static electric
dipole.
Setting
h =0 and
y =0 for simplicity, and using
PKV from Table 2 (with
q in place of
q ) for the dipole moment
P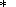 associated
with an
electrokinetic source, we have
associated
with an
electrokinetic source, we have

|
| Figure 6 |
 | (35) |
The field varies as l2, the area of the vertical inhomogeneity, and inversely as the cube of the distance R between source and detector. In Figure 6 we show how E varies with R (logarithmic scale) for q equal to 10-4 and for a range of l (10 m to 10 km), based on the above formula.
The range of applicability of the dipole approximation limits
R to values larger than about
3l, so the graphs
in Figure 6
do not extend down to values of
R which are below this limit. Even for a source comparable in size
to the origin of a large earthquake (1 km
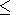 10 km), equation 35 gives a field at
a distance of 100 km from the
source which is three to five orders of magnitude less than the reported anomalies.
Incorporating the effects
of inhomogeneities in the conductivity in the crust could increase the field by several
times, but it is highly
unlikely to increase it by three to five orders of magnitude.
10 km), equation 35 gives a field at
a distance of 100 km from the
source which is three to five orders of magnitude less than the reported anomalies.
Incorporating the effects
of inhomogeneities in the conductivity in the crust could increase the field by several
times, but it is highly
unlikely to increase it by three to five orders of magnitude.
For a small source ( l =10 and 100 m) the field is detectable at distances close to the source, as seen in Figure 6. The graphs for l =1 km and l =10 km correspond to co-seismic effects. These are negligibly small, which is consistent with their absence in electrotelluric field measurements far from the epicenter. Here the term "co-seismic'' refers to EM signals generated at the focal area during the main shock, and not to seismic waves.
Consideration of the possible physical mechanisms for electrotelluric anomalies leads to the conclusion that the electrokinetic effect is the most appropriate candidate.
A few observations of anomalous electromagnetic emission in the ultra-low frequency (ULF) range (10-2 -10 Hz) have been reported. In 1964 two articles appeared dealing with the detection of anomalous magnetic impulses before an earthquake [Breiner, 1964; Moore, 1964]. The duration of these impulses indicated the disturbance was in the ULF range. The report by Fraezer-Smith et al., [1990] stimulated more interest in this field. This article reported ULF disturbances in the geomagnetic field before and after the magnitude 7.1 Loma Prieta earthquake. These disturbances appeared more than one month before the quake and were detected over several frequency channels. The most intense disturbance, in the range 0.1 to 0.2 Hz, began approximately three hours before the quake and exceeded background by two orders of magnitude. Analysis of the data indicated that it was not due to magnetic fluctuations in the earth's upper atmosphere nor to quake-induced detector motion. The authors concluded that the intense ULF disturbance was probably a magnetic precursor. Anomalies in the ULF range have also been reported in other seismically active regions [Fujinawa and Takahashi, 1998; Hayakawa et al., 1996; Kopytenko et al., 1993].
Several models have been developed to explain the geomagnetic phenomena associated with the Loma Prieta quake. The first was based on the induction effect [Draganov et al., 1991]. However, it was shown by others that this model requires unrealistic conditions, such as very large changes in the volume strain and a pore water pressure exceeding lithostatic values [Fenoglio et al., 1995; Gershenzon and Gokhberg, 1994]. On the other hand, using the same parameters as in the induction model, the electrokinetic effect has been shown in Section 3 and in the paper by Gershenzon and Gokhberg [1994] to give a magnetic disturbance three to five orders of magnitude greater than the induction effect.
The model using the electrokinetic effect was developed by Gershenzon and Gokhberg [1994]. It was shown that multiple cracks appearing in a sub-surface layer could account for the observed effect. This model was able to explain the frequency dependence as well as the magnitude. Fenoglio et al., [1995] presented a model, also based on the electrokinetic effect, with a more developed mechanical component, i.e. they showed that the source of the pore pressure gradient could be "failure of faults containing sealed compartments with pore pressures ranging from hydrostatic to lithostatic levels''. A similar idea was proposed earlier by Bernard [1992]. The pressure gradient in this case would be much larger than for the changes in the volume strain considered by Gershenzon and Gokhberg [1994]. The model of Fenoglio et al. [1995] could account for the observed effects at great distances from the mechanical source. Merzer and Klemperer [1997] proposed a model based on local conductivity changes in the earth's crust. In the presence of normal external geomagnetic variation, conductivity changes in the crust could lead to local changes in the magnitude of the geomagnetic variation. However, the proposed geometry of the region necessary to account for the effect, i.e. an infinite horizontal elliptic cylinder of diameter several kilometers and instantaneous changes in the conductivity of several orders of magnitude, extending throughout this region, seems to us to be unrealistic. If the region of high conductivity were not infinite, the electric field arising in this region, and the resulting geomagnetic disturbance, would be much less. Molchanov and Hayakawa [1998] developed a model based on the formation of multiple cracks in the focal area during the earthquake formation stage. Since crack formation is accompanied by electric charge separation (due to various mechanisms) an EM field will appear. The low frequency part of this field could reach the surface. We find that the energy associated with charge separation during crack formation is distributed over a broad frequency range and only a small part occurs in the ULF region. Our model also considers the formation of multiple cracks (not necessarily restricted to the focal area), and we find that the electrokinetic effect is a mechanism which provides considerably more energy in the ULF range, because it is controlled by the diffusion of water with a diffusion time comparable to the period of ULF emissions.

|
| Figure 7 |
 |
where the active region during the acquisition time DT is assumed to be a sphere of radius r. Figure 7 shows the variation of Bm with distance R from the source, for four different combinations of crack size and frequency. It is known that the crack size defines the spectral density of the signal through the diffusion relaxation time DTD and seismic impulse life time t. From Figure 7 we see that a 1m crack could account for the disturbance in the 5 to 10 Hz channel associated with the Loma Prieta quake, and a 20 m crack could account for the 0.01 to 0.02 Hz channel (see Gershenzon and Gokhberg [1994] for a more extensive discussion). In summary, Figure 7 shows that the Loma Prieta data could be accounted for by a local source lying within a water saturated layer and located within 1 km of the detector.
Over thirty years ago, Vorobyev proposed that earthquakes are the result of an electromagnetic storm within the crust. Although this hypothesis must be rejected on theoretical grounds, since the electrical conductivity in the crust is too high for charge separation to occur over the large distances required, experiments to detect RF emission at the surface before and during a quake have been performed for several years in Uzbekhistan by Vorobyev and collaborators [Mavlyanov et al., 1979; Vorobyev et al., 1975, 1976]. The same type of experiments were also conducted in Carpathia [Sadovsky et al., 1979] and the Caucasus [Gokhberg et al., 1979].
A Russo-Japanese collaboration resulted in further experiments in Japan [Gokhberg et al., 1982]. The authors reported intense electromagnetic emission (EME) at 81 kHz beginning 1.5 hours before a major quake (magnitude 6.1). The EME activity increased steadily with time until the main shock occurred, when it decreased abruptly. Twenty minutes later a large aftershock occurred and the EME activity decreased abruptly again, falling to the background level. This experiment initiated similar experiments in the RF range by several groups in various countries. One group in Japan reported twenty such occurrences over a two-year period [Oike and Yamada, 1994; Oike and Ogawa, 1986]. This group used a frequency of 163 kHz because of the low background activity at this frequency at their location. The associated quakes were all centered in Japan, had magnitudes greater than 6.0, and the EME was from four to twelve times background. Some evidence of EM emission relating to earthquakes in America also have been reported [Tate and Daily, 1989; Warwick et al., 1982]. Anomalies at 3 and 10 kHz and 41 and 54 MHz were observed before several earthquakes in Greece [Eftaxias et al., 2000, 2001; Varotsos et al., 1996b]. Further references to field experiments in the RF range may be found in Gokhberg et al. [1995].
It is difficult to compare the results of the several groups working in this area because of differences in detectors, frequency ranges, and discrimination techniques. Nevertheless there are some common morphological features of the phenomenon:
EME noise in the RF range can have several sources, some natural (e.g. atmospheric lightning) and some man-made (e.g. commercial radio broadcasting, industrial activities). These sources are all hard to eliminate, because multiple reflections from the ground and the ionosphere can cause a signal to propagate over large distances.
We now discuss possible models for EME anomalies. The simplest model identifies the EME source with the origin of the quake, and requires a mechano-electromagnetic transducer of some kind which is active only during the precursor period. A serious flaw in this model is that it requires an attenuation length for RF signals which is on the order of the typical depths at which quakes originate. It is easy to show that the attenuation length in the crust is much less than this.
Another model was developed by Gokhberg et al. [1985]. It involves the creation of a large-scale electrical current, of very low frequency, which extends to the earth's surface. The electric field associated with this current loop, though weak, could extend into the atmosphere and produce a lightning discharge at high altitude, where the ionization potential becomes small. The lightning discharge could be a source of secondary emission in the RF range. The idea that atmospheric processes could be a source of EME has also been considered by Fujinawa et al. [1997].
Sadovsky et al. [1979] suggested that electromagnetic anomalies were related to changes in the electrical characteristics of the environment about the measurement point. These changes could be related to pre-seismic processes, while the source of the electromagnetic fields could simply be background noise.
Malyshkov et al. [1998] proposed a model in which the earth's crust constantly emits EM signals associated with background elastic waves. These signals would normally be part of the background EM noise, but a change in these signals, i.e. an EME anomaly, could occur when an elastic wave propagates through the altered mechanical state of an earthquake preparation region (i.e. an altered stress state or an altered density of microcracks). However this model is based on laboratory experiments in the ultrasound range (kHz to MHz). It is difficult to see how an EM signal in the RF range could be produced by the low-frequency seismic waves (10-2 to 10 Hz) observed in field experiments.
From our viewpoint, the model developed here provides a natural framework for discussing the above RF phenomena. We will calculate the magnitude of the anomalies and discuss the circumstances under which they can be detected. But first we consider two different techniques which are applied in field experiments for monitoring SEM anomalies in the RF range. The first technique (simple averaging) is the usual one, in which all signals received during the acquisition window DT are averaged, and leads to equations (26) and (28). The second technique (which we shall call impulse averaging) is based on the supposition that the useful signals (as opposed to noise) are pulsed rather than continuous. In this technique only filtered signals above a present threshold are considered. In this case, the time between impulses (the "dead time'') does not influence the measurement. This technique corresponds to equations (27) and (29) when DT is large enough to count one pulse or a cluster of closely spaced pulses but small enough to exclude the dead time. As we mentioned at the end of Section 4, the ratio of Em (or Bm ) calculated using pulse averaging to Em (or Bm ) using simple averaging is of order (DfDT)1/2, which can be very large for reasonable values of Df and DT (here DT is the acquisition time for simple averaging). This means that impulse averaging can be much more sensitive than simple averaging in detecting RF anomalies, in agreement with RF field experiments [Gokhberg et al., 1986]. In the remainder of this section we shall present results based on the impulse averaging technique.

|
| Figure 8 |

|
| Figure 9 |
By use of the equations and figures presented here, we see that our model can explain the appearance of RF anomalies of order 10-100 m V/m under the following conditions.
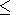 s0
s0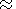 10-4(W
10-4(W m)-1 for
f =100 kHz).
m)-1 for
f =100 kHz).
This model cannot explain reported anomalies as large as 100 mV/m [Mavlyanov et al., 1979; Sadovsky et al., 1979; Vorobyev et al., 1975, 1976]. Such anomalies may be related to atmospheric phenomena (lighting activity) connected with pre-seismic processes [Fujinawa et al., 1997].

|
| Figure 10 |
This document was generated by TeXWeb (Win32, v.1.3) on October 28, 2000.