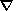 T) is strong even at Nu > 10(Ra > 105 ). For this reason, a regular circulation of the mantle material
is accompanied narrow jets, plumes, diapirs,
and floating-up thermals.
T) is strong even at Nu > 10(Ra > 105 ). For this reason, a regular circulation of the mantle material
is accompanied narrow jets, plumes, diapirs,
and floating-up thermals.
V. P. Trubitsyn and V. V. Rykov
Schmidt United Institute of Physics of the Earth, Russian Academy of Sciences, Bol'shaya Gruzinskaya ul. 10, Moscow, 123810 Russia
 40o. The initial state was modeled
by the present
mantle with a temperature distribution estimated from seismic tomography data. In
this state, the distributions of the
surface heat flux and mantle flow velocities are consistent with observations. The
continents in the initial state are
uniformly distributed over the mantle surface.
The long-term evolution of the mantle-continents system, lasting a few billions of
years, was calculated.
A numerical experiment conducted within the framework of this idealized model showed
that, for the most time, the
continents are located above mantle downwellings and move together with them. If
two mantle flows accidentally approach
one another, a zone arises that pulls adjacent continents in (along with underlying
mantle flows). As a result, mantle
downwellings and the related continents start joining. Our numerical experiment showed
that the continents first form
groups of four to five continents and a large supercontinent is then assembled from
these groups. The overheated mantle
under the supercontinent gives rise to new convective upwellings. As a result, the
supercontinent first divides into two
smaller supercontinents. Afterward, the latter also break up. One of the smaller
supercontinents (similar to Laurasia)
first breaks up into five continents, after which the second supercontinent (similar
to Gondwana) also divides. Afterward,
the continents scatter all over the mantle surface. The convergence and divergence
events repeatedly occur during the
evolution.
40o. The initial state was modeled
by the present
mantle with a temperature distribution estimated from seismic tomography data. In
this state, the distributions of the
surface heat flux and mantle flow velocities are consistent with observations. The
continents in the initial state are
uniformly distributed over the mantle surface.
The long-term evolution of the mantle-continents system, lasting a few billions of
years, was calculated.
A numerical experiment conducted within the framework of this idealized model showed
that, for the most time, the
continents are located above mantle downwellings and move together with them. If
two mantle flows accidentally approach
one another, a zone arises that pulls adjacent continents in (along with underlying
mantle flows). As a result, mantle
downwellings and the related continents start joining. Our numerical experiment showed
that the continents first form
groups of four to five continents and a large supercontinent is then assembled from
these groups. The overheated mantle
under the supercontinent gives rise to new convective upwellings. As a result, the
supercontinent first divides into two
smaller supercontinents. Afterward, the latter also break up. One of the smaller
supercontinents (similar to Laurasia)
first breaks up into five continents, after which the second supercontinent (similar
to Gondwana) also divides. Afterward,
the continents scatter all over the mantle surface. The convergence and divergence
events repeatedly occur during the
evolution.
Thermal convection is the driving force of global geodynamic processes in the Earth. A hot and lighter (due to thermal expansion) material ascends during the thermal convection; upon releasing its heat to the environment, this material becomes heavier and descends back into the mantle. This gives rise to a material circulation and heat flux maximums form above the mantle upwellings. The heat flux value is proportional to the convection velocity. The observed heat flux distribution over the Earth and variations in the thickness of the oceanic lithosphere are controlled by the thermal convection.
Thermal convection arises if the temperature increases downward with a superadiabatic gradient. The adiabatic gradient in the Earth is about 0.4 K/km, which gives a temperature drop through the mantle of about 1200 K (e.g. see [Trubitsyn, 2000]). An ascending material dilates and cools due to the decreasing pressure. If the real temperature in the Earth were lower than its adiabatic value, the ascending material would become colder and heavier than the surrounding medium just on the way, and its further ascent would become impossible. The temperature which an ascending material would have when reaching the surf ace is called a potential temperature. It is equal to the excess of the actual temperature of the material at a given point above the adiabatic temperature and therefore causes thermal convection in a nonviscous mantle. In order to induce thermal convection in a viscous mantle, the temperature should exceed this superadiabatic temperature by a value at which the buoyancy force of the material overcomes the viscous drag forces. The convection intensity characterized by the dimensionless Rayleigh number is proportional to this value of the superadiabatic temperature excess. Vigorous thermal convection in the mantle with a Rayleigh number of about 10 7 develops at a total superadiabatic temperature drop of about 2500 K. The onset of thermal convection in a Cartesian model with free-slip boundary conditions takes place at a critical Rayleigh number of 657. Given a superadiabatic temperature increment in the mantle as low as ~0.25 K, the mantle convection intensity corresponds to a Rayleigh number of about 103.
Compositional convection can develop in a multicomponent material. The process of chemical differentiation controlled the convection structure in the early period of the Earth's history, when the iron core was growing. Settling iron entrained silicates, and compositional convection occurred along with thermal convection. The gravitational energy converted into heat which continues to be released even presently, accounting for as much as 30% contemporary heat flux of the Earth. Geochemical evidence indicates that the growth of the core was largely accomplished over the first 60-100 Myr after the Earth's formation [McCulloch and Bennet, 1998]. According to the current ideas, the chemical differentiation contribution to the driving forces of the recent global geodynamics is much smaller than the contribution of thermal convection. However, the chemical differentiation and mineral transformations are essential to both the origin of the crust and anomalously low density and high strength of the continental lithosphere. Moreover, the study of the global repartitioning of isotopes gives constraints on their transport by mantle flows and on the evolution of the global convection structure. Since buoyancy of continents is due to the contrast of their mineralogical and chemical composition with respect to the mantle, the mantle convection with floating continents can be viewed as a special type of thermocompositional convection.
The thermal convection in the mantle is characterized by the following five major properties which control the contemporary geodynamics of the Earth.
(1) Although the mantle flow velocities are comparatively small (~1-10 cm/yr),
the mantle convection is nonstationary and
quasi-turbulent. The convective heat transfer contribution is characterized by the
Nusselt number Nu. The nonlinear
coupling between the heat and mass transfer processes (described by the term
V
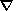 T) is strong even at Nu > 10(Ra > 105 ). For this reason, a regular circulation of the mantle material
is accompanied narrow jets, plumes, diapirs,
and floating-up thermals.
T) is strong even at Nu > 10(Ra > 105 ). For this reason, a regular circulation of the mantle material
is accompanied narrow jets, plumes, diapirs,
and floating-up thermals.
(2) The endothermal olivine-perovskite transition at a 660-km depth results in partial stratification of the mantle. Whereas the upper mantle became depleted at the expense of incompatible elements that escaped into the crust, the composition of the lower mantle material is close to the primordial composition. This gives rise to specific plumes generated in the primordial or recycled layer at the mantle base, crossing the phase transition boundary between the lower and upper mantle and appearing on the surface as hotspots. In the former, hotter mantle, the phase boundary effect was stronger, and the mixing of the upper and lower mantle material was episodic but fairly intense, entraining large volumes of the oceanic and partly continental crust toward the lower mantle bottom. As the mantle cooled, the phase boundary barrier weakened and hotspot plumes could develop into regular flows of the whole-mantle convection.
(3) The viscosity drastically drops with increasing temperature and increases with pressure. Under mantle conditions, the viscosity changes by more than 20 orders, from ~103 in basalt melts of magma chambers to ~1026 in cold lithosphere. Since during convection the average temperature abruptly increases in the upper and lower conductive boundary layers, asthenospheric low-viscosity layers arise at depths of 100 to 200 km and at the mantle base. Their thicknesses vary because the horizontal temperature variations associated with the thermal convection in mantle reach 300 K.
(4) The average temperature of lithosphere is much lower than the melting temperature. Therefore, the lithosphere material is more brittle compared to the rest of mantle, and sharp variations in stresses break up the lithosphere into plates that move, similar to a conveyer, over the Earth's surface. Rigid plates can move over and under one another only at small angles. The oceanic lithosphere can experience strong deformations and sink in subduction zones because, under the action of prolonged bending stresses, the lithosphere material acquires plasticity properties.
(5) Continents, occupying nearly one third of the Earth's surface, hinder the heat release from the mantle. With an average mantle flow of about 70 mW/m2 (without the radioactive heat of continental lithosphere), the oceanic heat flux is about 90 mW/m2 and its continental value is three times as small, about 30 mW/m2. Since continents restructure the heat released from the mantle, they should have a strong effect on the entire pattern of mantle convection. The mechanical and thermal coupling of mantle with continents is essential to the explanation of the continental lithosphere formation, the state of the mantle under continents, formation and breakup of supercontinents, and so on.
The first three properties of the mantle convection and their signatures in the global geodynamics have been studied over a few decades. In particular, these studies resulted in the creation of the kinematic theory of plate tectonics and the theory of mantle convection including phase transitions. Presently, comprehensive studies have been conducted on models of both layered convection [Allegre, 1982; Allegre et al., 1983; Anderson, 1981, 1982; DePaolo, 1980, 1981; DePaolo and Wasserburg, 1976, 1979; Dobretsov and Kirdyashkin, 1994; Jackson, 1998; Jacobsen and Wasserburg, 1979, 1981; Jeanloz and Knittle, 1989; O'Nions and Oxburg, 1983; O'Nions et al., 1979] and whole-mantle convection [Davies, 1974, 1979, 1984; Grand, 1987, 1994; Grand et al., 1997; Hoffmann and White, 1982; Jackson, 1998; Jordan, 1977; Van der Hilst, 1995; Van der Hilst et al., 1991, 1997]. Detailed numerical models of the present Earth have been constructed [Becker et al., 1999; Brunet and Machtel, 1998; Bunge et al., 1997; Kellogg et al. 1999; Machetel and Weber, 1991; Solheim and Peltier, 1994; Steinbach et al., 1993; Tackley, 1994, 1996]. Hypothetical geochemical models providing insights into the origin of various geochemical reservoirs have been analyzed [Tackley, 2000].
The recent successful development of the comprehensive theory of oceanic lithosphere have been mainly associated with works by Tackley[2000], Gurnis with coworkers [Zhong et al., 1998]. Since this theory includes rheological properties of the lithosphere in the equations of mantle convection, the bending and subduction of the oceanic lithosphere, as well as its breakup into rigid plates are not preset but are derived from the solution of a self-consistent set of equations.
Mantle convection including continents was first studied with immobile continents [Lowman and Jarvis, 1995, 1996; Nakanuki et al., 1997; Trubitsyn and Bobrov, 1994; Trubitsyn and Fradkov, 1985]. However, later it was understood that main significant features of global tectonics are controlled exactly by motions of continents nonlinearly coupled with mantle flows. Two approaches are applied to the modeling of the mantle convection interaction with mobile continents. Gurnis [1988] and Gurnis and Zhong [1991] calculated 2-D models which, rather than to use explicit equations describing motions of continents, represent continents as high-viscosity regions in the mantle whose motions are actually traced with the use of markers. One may state that this approach treats the mantle convection with floating continents in terms of thermocompositional convection. Trubitsyn and Rykov [1995, 1998a, 1998b, 2000; Trubitsyn et al., 1999] developed a different approach and laid down foundations of the theory of mantle convection with floating solid continents. The equations of mantle convection were complemented by the Euler equations describing the translatory motion and rotation of solid continents interacting with the mantle with one another. The theory of mantle convection with floating continents [Trubitsyn, 2000b; Trubitsyn and Rykov, 2000] treats the model of floating solid continents as a first approximation. This model determines the position and velocities of continents, temperature distributions within them, all mantle forces applied to the continents (to their surfaces submerged in the mantle), and forces involved in the collision of continents. Since the continent strain values are much smaller than the global displacements of continents, intracontinental strains and stresses can be calculated in the next approximation based on a different rheological model with external forces that are already found.
The theory of mantle convection with floating solid continents is based on numerical experiments, i.e. on the numerical solution of a system of equations describing the energy, mass, momentum and angular momentum transfer in the mantle-continents system. In their previous studies, these authors showed that continents are not passive bodies but can have a substantial effect on the evolution of mantle convection. Only within small intervals of the geological time scale may one consider them to be "frozen'' in the oceanic lithosphere. The continental lithosphere arises and exists a few billions of years solely because the floating continents are pulled toward cold mantle downwellings, which ensures the existence of a cold, highly viscous and strong continental lithosphere. Due to the thermal screening effect, the mantle under an immobile continent is inevitably heated (over time intervals of 200 to 500 Myr), giving rise to hot upwellings tending to melt and break up the continental lithosphere and crust.
This work presents results of a long numerical experiment with an idealized model including 12 contributions floating on a spherical mantle and accounting for their mechanical and thermal interaction with the mantle and between each other. The purpose of this work is to check whether continents floating on a spherical model can repeatedly assemble and diverge without invoking any additional controlling processes.
The thermal convection in a viscous mantle is described by distributions of the convective velocity vector Vi(x, y, z), temperature T(x, y, z) and pressure p(x, y, z). These unknown functions are found by solving a system of equations of the momentum, heat and mass transfer. In the Boussinesq approximation, these equations are written in the dimensionless form as
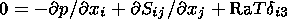 | (1) |
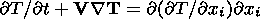 | (2) |
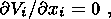 | (3) |
where Sij is the deviatoric tensor of viscous stresses
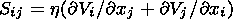 | (4) |
Ra is the Rayleigh number
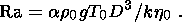 | (5) |
The following units were utilized for the reduction to the dimensionless form: mantle
thickness
D for length;
D/k for velocity;
D2/k for time;
T0 for temperature;
h0 for viscosity; and
h0k/D2 for
pressure and stresses. The pressure
p is measured from its hydrostatic distribution
p(z) determined from
the equation
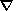 p0 = -r0g.
p0 = -r0g.
The continent is subjected to the gravitational force applied to its center and forces of coupling with the viscous mantle applied to surface elements of the submerged portion of the continent. Under the action of these forces, the continent floats in the mantle, moving over its surface and rotating about the vertical axis. Since the pressure and flow velocities in the mantle vary in time and space, both the vertical velocity of the continent center of gravity w0 and the angular velocities wx and wy of the continent rotation about the instantaneous horizontal axes x and y generally do not vanish.
Continents can descend (when above a downwelling) and ascend (above an upwelling) together with or relative to the mantle surface. Their downward or upward displacements can be different at different ends of a continent. In what follows, I consider only the horizontal displacements of the center of gravity of a continent and rotation of the continent about a local vertical axis, ignoring all of the remaining small effects, i.e. setting w0 = 0 and wx = wy = 0.
Since the gravity is in equilibrium with the buoyancy force, external forces applied to the continent reduce to the force of viscous coupling with the mantle, and the pressure p is measured from its hydrostatic distribution p0(z). Then, the Euler equations describing horizontal movements and rotations about an instantaneous vertical axis of a solid continent of an arbitrary shape reduce to a system of three dynamic equations and three kinematic equations [Trubitsyn, 2000; Trubitsyn and Rykov, 1998a, 1998b, 2000]:
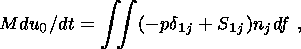 | (6) |
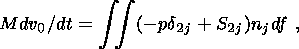 | (7) |
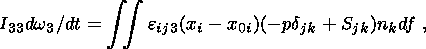 | (8) |
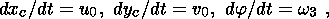 | (9) |
where M is the mass of the continent, I33 is its moment of inertia relative to the vertical axis, xc(t) and yc(t) are coordinates of its center of gravity, j is its angle of rotation, dij is the Kronecker delta equal to 1 at i=j and 0 at i j, and eijk is the Levi-Civita symbol equal to 0 for any two coinciding indexes, 1 for an even transposition of indexes from 1, 2, 3, and - 1 if such a transposition is uneven.
Since the dimension relationships imply that, similar to the equation of the momentum
transfer in a viscous liquid (1),
the inertial terms on the left-hand side of equations (6)-(8) have an order of magnitude
of
kr/m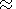 10-23,
these terms can be set at zero. Then, the Euler equations governing the motions of
continents give six relations
for six unknowns (coordinates of the continent center of gravity
xc(t) and
yc(t), rotation angle of the continent
j and its velocities
u0(t),
v0(t) and
w3(t) )
10-23,
these terms can be set at zero. Then, the Euler equations governing the motions of
continents give six relations
for six unknowns (coordinates of the continent center of gravity
xc(t) and
yc(t), rotation angle of the continent
j and its velocities
u0(t),
v0(t) and
w3(t) )
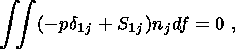 | (10) |
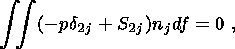 | (11) |
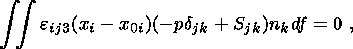 | (12) |
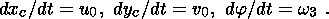 | (13) |
The equation describing the distribution of temperature Tc within a solid continent in an initial immobile system of coordinates reduces to the heat conduction equation with the advective heat transfer at a continent velocity u,
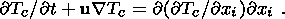 | (14) |
Equations of mantle convection (1)-(3), motion of a continent (6)-(8) and heat transfer within the continent (14) are coupled via boundary conditions.
As mentioned above, the impermeability and free-slip condition is adopted at the lower and lateral boundaries of the model region (the normal component of velocity and the tangential components of viscous forces vanish):
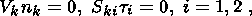 | (15) |
where nk is the unit vector normal to a given surface and ti are unit vectors tangential to the surface.
The impermeability and no-slip condition is adopted at the boundaries of moving solid continents, which means that the boundary velocities of the liquid mantle and a continent coincide,
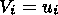 | (16) |
at the entire surface of the continental portion submerged in the mantle.
The temperature at the lower surface of the region is fixed at T = 1. The zero heat flux condition is adopted at the lateral boundaries (in the case of a finite region):
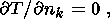 | (17) |
where nk is the unit vector normal to the lateral surface of the region.
The mantle temperature at the upper free surface is zero ( T = 0) only in the oceanic area outside the continent.
The continuity condition is adopted for the temperature and heat flux at the mantle-continent contact boundary:
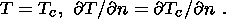 | (18) |
At the upper surface of the continent, the temperature is set at zero:
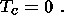 | (19) |
Thus, the mathematical problem is reduced to the following. There are three unknown functions describing the mantle convection (mantle flow velocity vector Vi(x, y, z, t), temperature distribution T(x, y, z, t) and pressure distribution p(x, y, z, t) and four unknown functions of time describing the motion of a continent as a whole (two instantaneous translatory velocity components of the center of gravity u0(t) and v0(t), one instantaneous angular velocity component of the continent rotating about its center of gravity w(t) and the temperature distribution within the continent Tc(x, y, z, t). They are found from a system of coupled equations: three differential equations of convection (1)-(3) and three integral equations (10)-(12), derived from the Euler equations, and the equation of heat transfer in the continent (14). If the position and velocities of the continent at a given time moment u0(t), v0(t) and w(t) are known, equation (9) provides its position at the next time moment. The constants of integration of the differential equations are found from boundary conditions (14)-(16).
The problem with a freely floating continent differs from the known problem with an immobile continent in that the boundary conditions for flow velocities and temperature at the mantle-continent boundary are specified for the position occupied by the floating continent at each given time moment. The current position and velocity of the continent are not known a priori but are found by solving the whole system of coupled differential equations.
In the case of a few continents, equations of motion (10)-(13) and temperature (14) are written out separately for each continent. Moreover, a collision of solid continents requires that the condition of their impenetrability into one another be fulfilled. For this purpose, at collision time moments the forces of viscous coupling with the mantle are complemented by a repulsive force applied at the contact area of the continents and acting in the direction opposite to their relative velocity. The magnitude of this force is found by fitting the condition of impenetrability of the contacting continents into one another at a given time moment.
The mantle is modelled by a spherical viscous shell. The free-slip condition is adopted at its lower (core-mantle) boundary and the temperature is fixed, T = T0. The continents are modelled by thick solid discs floating, like ships, in the mantle. The no-slip condition is adopted at the continent surface submerged in the mantle (at the base and lateral surface); i.e. the normal and tangential boundary velocity components of the mantle and continent coincide. The thickness of continental portions jutting out above the mantle is ignored. The temperature at the upper surface is set at zero. A zero temperature is also accepted for the upper surface of mantle unoccupied by continents.
The mantle viscosity is set constant, and phase transitions in mantle were not accounted
for. The Rayleigh number,
characterizing the mantle convection intensity, was set equal to Ra = 107. The thermal diffusivity was taken to be
the same in continents and mantle and equal to 2 10-6 m2/s. All continents had the same thickness, namely 250 km.
10-6 m2/s. All continents had the same thickness, namely 250 km.
At the initial moment, the continents were nearly uniformly distributed throughout the mantle surface. Their centers had latitudes q =36o, 90o and 154o and longitudes j =0o, 90o, 180o and 270o. The continents were specified as octagons differing in shape. For simplicity, their size and shape were taken from the condition that, at the initial moment, the coordinates of their angular points lie on q and j coordinate lines of the angular grid spaced (along great circles) at dq =36o and dj =40o.
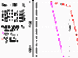
|
| Figure 1a |

|
| Figure 1b |
As the initial temperature distribution, we took the present mantle temperature distribution. In a first approximation, the laterally averaged temperature distribution is known [Solheim and Peltier, 1994; Tackley, 1996; Tackley et al., 1994; Trubitsyn and Rykov, 2000]. Figures 1a and 1b) presents simplified mantle distributions of the adiabatic temperature (rose), superadiabatic, or potential temperature characterizing the convection intensity (black) and total temperature (red). Since lateral variations in temperature are on the order of up to 300 K, they can be considered as corrections to the radial temperature distribution and can be found under the assumption that lateral density variations in the mantle are proportional to variations in seismic velocities [Anderson, 1989]. The seismic conversion factor dlnr/dlnVs is usually found from data of laboratory measurements and model calculations for minerals. Kaban and Schwintzer [2000] estimated it from the comparison of seismic tomography data with gravity anomalies. A density ( r ) distribution was first found from oceanic mantle gravity data. The comparison of this distribution with S wave velocities provided the dlnr/dlnVs estimates in the oceanic mantle. The seismic density conversion factor varies considerably with depth. However, since the kinematic evolution of continents was calculated at a constant viscosity, we assumed for simplicity that dlnr/dlnVs is equal to its average value which is about 0.1.
The mantle density depends on both temperature and chemical-mineralogical composition.
Thermal convection in the mantle
mixes the material, thereby attenuating variations in its composition, but gives
rise to lateral variations in temperature.
Assuming that density variations are mainly due temperature,
r = r0(1-aT) and setting the thermal expansion coefficient
a at 2 10-5,
we obtain that the coefficient of conversion of seismic
tomography data into temperature
is
dlnVs/dt =
-2
10-5,
we obtain that the coefficient of conversion of seismic
tomography data into temperature
is
dlnVs/dt =
-2 10-4 K-1. We took the
S wave velocity model distribution from
[Ekstrom and Dziewonski, 1998].
10-4 K-1. We took the
S wave velocity model distribution from
[Ekstrom and Dziewonski, 1998].
Note that the approximation of a chemically homogeneous mantle does not apply to the continental lithosphere. Since the continental lithosphere moves together with a continent and its material is not involved in the convective mixing process, chemical heterogeneities must have arisen in the continental lithosphere during a few billions of years. Volatiles could have transported iron (as well as other elements and compounds) from the continental lithosphere into the crust. According to Forte and Perry [2000], the iron deficit makes the anomalous cold continental lithosphere considerably lighter. Density changes caused by the iron deficit and by temperature are comparable. On the other hand, seismic velocities depend only slightly on chemical variations.
The initial temperature distribution and coordinates of continents were substituted into the equations of thermal convection with floating continents (1)-(18). The model results computed for the evolution of the mantle-continents system are presented in Frames 0000-4290. The numbers of the plates are chosen for convenience to coincide with time moments (in million of years) of the convection pattern and configuration of continents shown.
For the convenience of copying animated illustrations (of a few megabytes in volume), they are divided into five groups. Group 1 consists of frames 0000a and 0000b showing the initial conditions.
 |
| Group 2 |
 |
| Group 3 |
 |
| Group 4 |
 |
| Group 5 |
Figure 1a presents the initial (laterally averaged) temperature distribution (adiabat in rose, superadiabatic temperature in black and total temperature in red). Figure 1b shows the initial configuration of continents and the calculated heat flux distribution consistent with the initial 3-D temperature distribution. The outer surface is shown as a developed spherical surface centered at q =90o and j =0o. The continents are colored black. The heat flux from the mantle (in units of mW/m 2 ) is presented as a color plot with its scale shown in the left-hand part. Maximums (red) and elevated values (rose and yellow) of the heat flux coincide with mid-ocean ridges and volcanic zones. The system of equations of convection with floating continents was numerically solved in spherical coordinates using finite-difference iterations [Trubitsyn and Rykov, 1998b, 2000]. The continents were represented as spherical caps floating over the sphere. The initial temperature distribution within the disc continents considered can be arbitrarily taken because its further evolution is controlled solely by the solution of the equations. For simplicity, it was taken to coincide with the mantle temperature distribution derived from seismic tomography data in the area occupied by a given continent.
Given the initial temperature distribution and position of continents at t=t1=0, the temperature distribution in mantle and continents at the next time moment t2=t1+dt is found from equations (2) and (14). This new distribution is then substituted into (1), and mantle flow velocities are found. They are used for the determination of viscous forces applied to the continents and their velocities, after which the continents are rotated and moved in accordance with these velocities and time interval dt.
Frame 0006 shows the position of continents and distributions of heat flux and mantle flow velocities calculated at the time moment t=t2=6.6 Myr. The velocity scale is specified by the length of the arrow shown in the left. The time is measured in millions of years.
The next frames (0013 to 4290) present the complete model evolution of the "heated
viscous mantle-floating solid continents''
system. The model results show that the continents first move in the mantle flow
field consistent with the initial
temperature distribution and are drawn into downwelling areas by a time moment of
t 60 Myr (Frame 0065).
Note that the calculation of long-term evolution of a 3-D spherical model a very
fast computer. All results presented
in this paper were obtained on a Pentium-III PC, and we were compelled to use rather
rough computational meshes
( R
60 Myr (Frame 0065).
Note that the calculation of long-term evolution of a 3-D spherical model a very
fast computer. All results presented
in this paper were obtained on a Pentium-III PC, and we were compelled to use rather
rough computational meshes
( R q
q j=326
j=326 36
36 72 and
R
72 and
R q
q j=16
j=16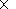 16
16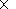 32 ). Both meshes
gave qualitatively similar results, but the finer mesh gave a somewhat smoother heat
flux distribution and somewhat
smaller velocities.
32 ). Both meshes
gave qualitatively similar results, but the finer mesh gave a somewhat smoother heat
flux distribution and somewhat
smaller velocities.
The continents tend to join into groups after about 100 Myr
(Group 2).
The possible mechanism of this process
consists in that each downwelling sucks in adjacent floating continents (like chips
of wood in a whirlpool).
However, each continent remains above its mantle downwelling and most time moves
together with it because the
continent-mantle viscous coupling is very strong at viscosity of about
1022 Pa s. For this reason,
not only the
continents but also cold mantle downwellings converge. The suction force of the resulting
group of downwellings
increases and pulls in even remote continents. By the time moment
t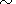 250-300 Myr (Frames 0253 and 0305)
two groups
of three and five continents form. At the time moments
t =351 and 409 Myr (Frames 0351 and 0409) only outlines of
the continents are shown to demonstrate that they occupy the coldest areas with minimum
heat fluxes.
250-300 Myr (Frames 0253 and 0305)
two groups
of three and five continents form. At the time moments
t =351 and 409 Myr (Frames 0351 and 0409) only outlines of
the continents are shown to demonstrate that they occupy the coldest areas with minimum
heat fluxes.
By the time
t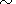 500 Myr (Frame 0500) both
groups of continents actually join to form an elongated supercontinent
including ten of twelve continents.
At the time
t =585 Myr (Frame 0585) the newly formed continent is most clearly
seen in a hemisphere centered at ( q =120o,
j =20o). The next frame (Frame 0585b)
shows only outlines of
the continents thereby displaying heat flux minimums. Frame 0585c presents,
for the same time, the temperature distribution in mantle
at a depth of 300 km, i.e. under the continents 250 km thick. This frame
demonstrates that the floating continents
invariably tend to occupy areas above mantle downwellings.
500 Myr (Frame 0500) both
groups of continents actually join to form an elongated supercontinent
including ten of twelve continents.
At the time
t =585 Myr (Frame 0585) the newly formed continent is most clearly
seen in a hemisphere centered at ( q =120o,
j =20o). The next frame (Frame 0585b)
shows only outlines of
the continents thereby displaying heat flux minimums. Frame 0585c presents,
for the same time, the temperature distribution in mantle
at a depth of 300 km, i.e. under the continents 250 km thick. This frame
demonstrates that the floating continents
invariably tend to occupy areas above mantle downwellings.
At the time moment
t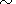 700 Myr (Frame 0689) the
supercontinent starts breaking up into two groups, each consisting
of five closely spaced continents. A band of hot mantle upwellings arises between
these groups, which diverge by 1000 km
over a period of 130 Myr (Frame 0721). As
seen from Frame 0786, each group of continents overlies contiguous downwellings.
However, beginning from the time
t
700 Myr (Frame 0689) the
supercontinent starts breaking up into two groups, each consisting
of five closely spaced continents. A band of hot mantle upwellings arises between
these groups, which diverge by 1000 km
over a period of 130 Myr (Frame 0721). As
seen from Frame 0786, each group of continents overlies contiguous downwellings.
However, beginning from the time
t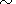 900 Myr (Frame 0916) a hot,
gradually strengthening mantle upwelling arises under
the middle area of the group shown in the upper parts of Frames 0916 to 1014.
Its lateral size reaches about 3000 km
at
t
900 Myr (Frame 0916) a hot,
gradually strengthening mantle upwelling arises under
the middle area of the group shown in the upper parts of Frames 0916 to 1014.
Its lateral size reaches about 3000 km
at
t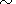 1200 Myr (Frame 1209). By
the time moment
t
1200 Myr (Frame 1209). By
the time moment
t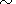 1400 Myr
(Frame 1404) the upper group divides into two sets of three and two
continents.
1400 Myr
(Frame 1404) the upper group divides into two sets of three and two
continents.
During the time period from 1600 to 2100 Myr (Frames 1631 to 2100) the continents are actually dispersed over the sphere, forming groups of two to four continents.
Afterward the process of repeated assemblage of continents starts. By the time moment
t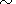 2400 Myr (Frame 2405) a
supercontinent incorporating four continents forms in the lower right-hand part of
the region. At
t
2400 Myr (Frame 2405) a
supercontinent incorporating four continents forms in the lower right-hand part of
the region. At
t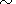 2600 Myr
(Frame 2632) a hot mantle upwelling arises, as previously, under its
middle part and detaches two upper continents
from the supercontinent.
2600 Myr
(Frame 2632) a hot mantle upwelling arises, as previously, under its
middle part and detaches two upper continents
from the supercontinent.
By the time
t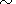 3000 Myr (Frame 3022) two
closely spaced groups of continents form near the south pole.
3000 Myr (Frame 3022) two
closely spaced groups of continents form near the south pole.
At the time moments
t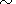 3388 Myr and
t
3388 Myr and
t 3445 Myr (Frames 3388a and 3445a)
a new supercontinent joining ten of twelve
continents is clearly seen to exist at the south pole. As seen from Frame 3388b,
no continents are present at the north
pole. Frame 3388c showing contours of the continents displays that the
continents overlie the coldest mantle regions,
as is evident from the heat flux and temperature fields. Frames 4290a to 4290c exhibit a similar pattern. This explains
the fact that, in spite of the heat screening effect of continents, the mantle at
depths of 200-300 km under the present
continents is colder than under oceans by 200o, which makes the continental
lithosphere thick, highly viscous and strong.
3445 Myr (Frames 3388a and 3445a)
a new supercontinent joining ten of twelve
continents is clearly seen to exist at the south pole. As seen from Frame 3388b,
no continents are present at the north
pole. Frame 3388c showing contours of the continents displays that the
continents overlie the coldest mantle regions,
as is evident from the heat flux and temperature fields. Frames 4290a to 4290c exhibit a similar pattern. This explains
the fact that, in spite of the heat screening effect of continents, the mantle at
depths of 200-300 km under the present
continents is colder than under oceans by 200o, which makes the continental
lithosphere thick, highly viscous and strong.
The goal of this work was to calculate the long-term evolution of the "mantle-floating
continents'' system in terms of a
3-D spherical model, to gain insights into the mechanism of the continental drift
and to demonstrate that continents
are capable of assembling and dispersing. The computation of the long-term evolution
of a 3-D model is time-consuming
and requires the use of a high-performance computer. Since personal computers only
were at our disposal, we chose the
simplest model with coarse computational meshes ( R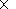 q
q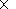 j =326
j =326
 36
36
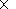 72 and even
R
72 and even
R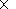 q
q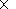 j =16
j =16
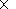 16
16
 32).
For this reason, the inferred results are mostly of qualitative value. Moreover,
dimensional velocities and times
depend on the chosen value of thermal diffusivity. A twofold decrease in this value
increases twice all computing
time intervals. The use of a model with variable parameters and a finer mesh can
change
the resulting values of the heat flux, temperature and velocities of mantle flows
and continents. However, as is
evident from computations of 2-D Cartesian models, basic evolutionary stages of the
mantle-continents system remain
the same even if the mesh step changes by a factor of 10 and more.
32).
For this reason, the inferred results are mostly of qualitative value. Moreover,
dimensional velocities and times
depend on the chosen value of thermal diffusivity. A twofold decrease in this value
increases twice all computing
time intervals. The use of a model with variable parameters and a finer mesh can
change
the resulting values of the heat flux, temperature and velocities of mantle flows
and continents. However, as is
evident from computations of 2-D Cartesian models, basic evolutionary stages of the
mantle-continents system remain
the same even if the mesh step changes by a factor of 10 and more.
The calculations showed that motions of continents are not chaotic and passive. They are governed by equations the mass, heat and momentum transfer in the mantle-continents system, and the structure of mantle flows is strongly affected the presence and movements of continents.
Since mantle downwellings attract the continents floating over the surface, the continents reside most of the time above these cold downwellings and move together with them. Since each mantle downwelling attracts all adjacent continents, continents tend to join. This process is favored by the fact that, due to viscous coupling between the continents and underlying downwellings, the latter also tend to assemble. This results in the formation of a joint system of downwellings capable of attracting even remote continents.
Due to the heat screening effect of continents, the mantle under a supercontinent is heated, its material becomes lighter, and cold mantle downwellings weaken and are replaced by hot mantle upwellings. Since the heat accumulation process is more intense under the middle part of the supercontinent, its breakup is more probably in the middle.
Evidently, other processes exist that affect the formation and breakup of supercontinents. Since continents hinder the heat release from the mantle, they decrease, to an extent, the intensity of convection make it less chaotic. In the interaction between the mantle convection and continents, the former introduces elements of chaos, whereas the continents have a regulating effect.
Allegre, C. J., Chemical geodynamics, Tectonophysics, 82, 109-132, 1982.
Allegre, C. J., S. R. Hart, and J. F. Minster, Chemical structure and the evolution of the mantle and continents determined by inversion of Nd and Sr isotopic data, Earth Planet. Sci. Lett., 66, 177-213, 1993.
Anderson, D. L., Hotspots, basalts and the evolution of the Earth, Science, 213, 82-89, 1981.
Anderson, D. L., Isotopic evolution of the mantle, Earth Planet. Sci. Lett., 57, 13-24, 1982.
Anderson, D. L., Theory of the Earth, Blackwell Scientific Publications, Boston, 1989.
Becker, T. W., J. B. Kellogg, and R. J. O'Connell, Earth. Planet. Sci Lett., 151, 351, 1999.
Brunet, D., and Ph. Machtel, Large-scale tectonic features induced by mantle avalanches with phase, temperature, and pressure lateral variations of viscosity, J. Geophys. Res., 103, 4920-4945, 1998.
Bunge, H. P., M. A. Richards, and J. R. Baumgardner, A sensitivity study of the three-dimensional spherical mantle convection at 108 Rayleigh number: Effects of depth-dependent viscosity, heating mode, and endothermic phase change, J. Geophys. Res., 102, 11,991-12,007, 1997.
Davies, G. F., Whole mantle convection and plate tectonics, Geophys. J. Roy. Astron. Soc., 49, 459-486, 1974.
Davies, G. F., Earth's neodymium budget and structure and evolution of the mantle, Nature, 290, 208-213, 1979.
Davies, G. F., Geophysical and isotopic constraints on mantle convection: an interim synthesis, J. Geophys. Res., 89, 6017-1040, 1984.
Davies, G. F., Penetration of plates and plumes through the mantle transition zone, Earth Planet. Sci. Lett., 136, 363-379, 1995.
Davies, G. F., and M. A. Richards, J. Geol., 100, 151, 1992.
DePaolo, D. J., Crustal growth and mantle evolution, Geochem. Cosmochem. Acta, 44, 1185-1196, 1980.
DePaolo, D. J., Nd isotopic studies: Some new perspectives on Earth structure and evolution, EOS, 52, 137-140, 1981.
DePaolo, D. J., and G. J. Wasserburg, Nd isotopic variations and petrogenic models, Geophys. Res. Lett., 3, 249-252, 1976.
DePaolo, D. J., and G. J. Wasserburg, Petrogenic mixing models and Nd-Sr isotopic patters, Geochem. Cosmochem. Acta, 43, 615-627, 1979.
Dobretsov, N. L., and A. G. Kirdyashkin, Deep Geodynamics, NITs OIGGM SO RAN, Novosibirsk, 1994 (in Russian).
Ekstrom, G., and A. M. Dziewonski, The unique anisotropy of the Pacific upper mantle, Nature, 394, 168-172, 1998.
Forte, A. M., and H. K. C. Perry, Geodynamic evidence for a chemically depleted continental tectonosphere, Nature, 290, 1940-1944, 2000.
Grand, S. P., Tomographic inversion for shear velocity beneath the north American plate, J. Geophys. Res., 92, 14,065-14,090, 1987.
Grand, S. P., Mantle shear structure beneath the Americas and surrounding oceans, J. Geophys. Res., 99, 11,591-11,621, 1994.
Grand, S. P., R. D. Van der Hilst, and S. Widiyantoro, Global seismic tomography: a snapshot of convection in the Earth, GSA Today, 7, 1-4, 1997.
Gurnis, M., Large-scale mantle convection and aggregation and dispersal of supercontinents, Nature, 332, 696-699, 1988.
Gurnis, M., and S. Zhong, Generation of long wavelengh heterogeneity in the mantle dynamics interaction between plates and convection, Geophys. Res. Lett., 18, 581-584, 1991.
Hoffmann, A. W., and W. M. White, Mantle plumes from ancient crust, Earth Planet. Sci. Lett., 57, 421-436, 1982.
Jackson, I., Elasticity, composition and temperature of the Earth's lower mantle, Geophys. J. Intern., 134, 291-311, 1998.
Jacobsen, S. V., and G. J. Wasserburg, The mean age of mantle and crustal reservoirs, J. Geophys. Res., 84, 7411-7427, 1979.
Jacobsen, S. V., and G. J. Wasserburg, Transport models for crust and mantle evolution, Tectonophysics, 75, 163-179, 1981.
Jeanloz, R., and E. Knittle, Density and composition of the lower mantle, Phil. Trans. Roy. Astr. Soc. L., A328, 337-389, 1989.
Jordan, T. H., Lithospheric slab penetration into the lower mantle beneath the Sea of Okhotsk, J. Geophys., 43, 473-496, 1977.
Kaban, M. K., and P. Schwintzer, Seismic tomography and implications for models of the Earth's mantle, Geoforschung Zentrum, Potsdam, Scientific Technical Report STR00/01, 2000.
Kellogg, L. H., B. H. Hager, and R. D. Van der Hilst, Science, 263, 1881, 1999.
Lowman, J. P., and J. T. Jarvis, Mantle convection models of continental collision and breakup incorporating finite thickness plates, Phys. Earth Planet. Inter., 88, 53-68, 1995.
Lowman, J. P., and J. T. Jarvis, Continental collisions in wide aspect ratio and high Rayleigh number two-dimensional mantle convection models, J. Geophys. Res., 101, 25,485-25,497, 1996.
Machetel, P., and P. Weber, Intermittent layered convection in a model mantle with an endothermic phase change at 670 km, Nature, 350, 55-57, 1991.
McCulloch, M. T., and V. C. Bennett, Early differentiation of the Earth: an isotopic perspective, Earth's mantle, I. Jackson, Ed., Cambridge Univ. Press, 1998.
Nakanuki, T., D. A. Yuen, and S. Honda, The interaction of plumes with transitions zone under continents and oceans, Earth and Planet. Sci. Lett., 146, 379-391, 1997.
O'Nions, R. K., and E. R. Oxburg, Heat and helium in the Earth, Nature, 306, 429-431, 1983.
O'Nions, R. K., N. M. Evensen, and P. J. Hamilton, Geochemical modeling of mantle differentiation and crustal growth, J. Geophys. Res., 84, 6091-6101, 1979.
Solheim, L. P., and W. R. Peltier, Phase boundary deflections at 660-km depth and episodically layered isochemical convection in the mantle, J. Geophys. Res., 99, 15,861-15,875, 1994.
Steinbach, V., D. A. Yuen, and W. Zhao, Instability from phase transitions and the timescales of mantle evolution, Geophys. Res. Lett., 20, 1119-1122, 1993.
Tackley, P. J., Effects of strongly variable viscosity on three-dimensional compressible convection in planetary mantles, J. Gephys. Res., 101, 3311-3332, 1996.
Tackley, P. J., Mantle convection and plate tectonics: Toward an integrated physical and chemical theory, Science Print, 2888, 2002-2007, 2000.
Tackley P. J., D. J. Stevenson, G. A. Glatzmaier, and G. Schubert, Effect of multiple phase transitions in three-dimensional spherical model of convection in Earth's mantle, J. Geophys. Res., 99, 15,877-15,901, 1994.
Trubitsyn, V. P., Phase transitions, compressibility, thermal expansion, and adiabatic temperature in the mantle, Izvestiya, Physics of the Solid Earth, 36, 101-113, 2000a.
Trubitsyn, V. P., Principles of the tectonics of floating continents, Izvestiya, Physics of the Solid Earth, 36, 101-113, 2000b.
Trubitsyn, V. P., and A. M. Bobrov, Evolution of the mantle convection after breakup of a supercontinent, Izvestia, Physics of the Solid Earth, 29, 768-778, 1994.
Trubitsyn, V. P., and A. S. Fradkov, Convection under continents and oceans, Izvestia, Physics of the Solid Earth, 21, 491-498, 1985.
Trubitsyn, V. P., and V. V. Rykov, A 3-D numerical model of the Wilson cycle, J. Geodyn., 20, 63-75, 1995.
Trubitsyn, V. P., and V. V. Rykov, A self-consistent 2-D model of mantle convection with a floating continent, Russian J. Earth Sci., 1, (1), 1998a, http://eos.wdcb.rssi.ru/tjes/TJE98001/TJE98001.htm
Trubitsyn, V. P., and V. V. Rykov, Three-dimensional spherical models for mantle convection, continental drift, and the formation and disintegration of supercontinents, Russian J. Earth Sci., 1, (2), 1998b, http://eos.wdcb.rssi.ru/tjes/TJE98005/TJE98005.htm
Trubitsyn, V. P., and V. V. Rykov, Three-dimensional spherical models of mantle convection with floating continents, U.S. Geological Survey Open File Report 00-218, 88, 2000.
Trubitsyn, V. P., V. V. Rykov, and W. Jacoby, A self-consistent 2-D model for the dip angle of mantle downflow beneath an overriding continent, J. Geodyn., 28, 215-224, 1999.
Turcott, D. L., and G. Schubert, Geodynamics: Applications of Continuum Physics to Geological Problems, Wiley, New York, 1982.
Van der Hilst, R. D., Complex morphology of subducted lithosphere in the mantle beneath Tonga trench, Nature, 374, 154-157, 1995.
Van der Hilst, R. D., E. R. Engdahl, W. Spakman, and G. Nolet, Tomographic imaging of subducted lithosphere below northwest Pacific island arc, Nature, 353, 37-43, 1991.
Van der Hilst, R. D., S. Widiyantoro, and E. R. Engdahl, Evidence for deep mantle circulation from global tomography, Nature, 386, 578-584, 1997.
Zhong, S. M., M. Gurnis, and L. Moresi, Role of foults, nonlinear rheology, and viscosity structure in generating plates from instaneous mantle flow models, J. Geophys. Res., 103, 15,225-15,268, 1998.