 Ktg by using a complex
of geological and
geophysical prognostic features both stationary
(or slightly changing during the observation period
and the time of strong earthquake preparation) and nonstationary.
Ktg by using a complex
of geological and
geophysical prognostic features both stationary
(or slightly changing during the observation period
and the time of strong earthquake preparation) and nonstationary.
G. A. Sobolev and A. D. Zavyalov
Institute of Physics of the Earth, Russian Academy of Sciences, Moscow
Yu. S. Tyupkin
National Geophysical Committee of Russian Federation
There are several methods of intermediate-term earthquake prediction based on the study of weak seismicity variations including the methods of formalized determination of the seismic quiescence [Wyss and Habermann, 1988; Zschau, 1995]. The combinations of seismological parameters are used in the methods of earthquake prediction proposed by Gabrielov et al. [1986]; Kosobokov and Keilis-Borok [1990]; Sobolev et al. [1991]. In the most of the mentioned papers, the significance of an anomaly of weak seismicity is proved by statistical approach.
The modeling in the laboratory likewise shows that in the process of deformation of rocks and artificial materials the successive stages of accumulation of cracks, their growth, and concentration of the cracking process at the place of the macrofailure are observed before the appearance of a macrofailure of the shear type [Sobolev and Koltsov, 1988]. The first stage occurs against the background of the growing load and increase of acoustic activity (the number of acoustic signals N per a unit of time). At the load maximum, as a result of the cracks stress fields interaction, the process of enlargement of cracks becomes intensive and results in lower acoustic activity (quiescence) because of cessation of the appearance of small cracks due to partial discharge of the medium and the change of stress tensor. The final stage shows localization and acceleration of deformations and the appearance of an echelon of cracks. This stage is characterized by the secondary (foreshock) activation confined to the place of the future macrofailure. This representation correlates, to a considerable extent, with the kinetic concept of solid bodies strength [Zhurkov, 1968] and forms the physical basis for the methods and algorithms of intermediate-term earthquake prediction. The intermediate-term prediction is understood as the place and magnitude prediction of an earthquake in the interval up to several years.
The Map of Expected Earthquakes (MEE) algorithm of the intermediate-term earthquake prediction was elaborated 15 years ago [Sobolev et al., 1991]; it received practical approval on the earthquake catalogs of different seismoactive regions of the world: the Caucasus, Kamchatka, Turkmenistan, Kyrgyzstan, Southern California, Northeastern and Southeastern China.
The MEE algorithm allows to calculate the maps of spatial distributions
of the conditional probability of earthquakes of the energy classes
K  Ktg by using a complex
of geological and
geophysical prognostic features both stationary
(or slightly changing during the observation period
and the time of strong earthquake preparation) and nonstationary.
Ktg by using a complex
of geological and
geophysical prognostic features both stationary
(or slightly changing during the observation period
and the time of strong earthquake preparation) and nonstationary.
The MEE algorithm is based on the principle of space-time scanning of the earthquakes catalog of the studied seismically active region and the subsequent determination of areas with a higher probability of expectation of a strong earthquake, calculated by the well-known Bayes formula for a set of parameters. In this study, all prognostic parameters are represented as space-time distributions of anomalous deviations from the corresponding long-term (background) level normalized by the value of the mean square error of its determination, and have retrospective statistic evaluations of the effectiveness of prediction for the chosen alarm level. If the data on the stationary prognostic features is available and sufficient (for example, tectonic faults or their crossing in the elementary spatial cell and the rate of vertical movements), the studied area is preliminarily differentiated by the level of stationary conditional probability of a strong earthquake occurrence. If such data are absent then instead of the stationary conditional probability based on seismostatistics only the unconditional probability is calculated, the values of which are identical at all points of the region.
The following seismological parameters are used in MEE algorithm at the present study:
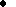 the density of seismogenic faults
Ksf;
the density of seismogenic faults
Ksf;
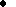 the slope of the recurrence plot
g;
the slope of the recurrence plot
g;
 the number of weak earthquakes occurring in
a unit of time
as an indicator of seismic quiescence and activation;
the number of weak earthquakes occurring in
a unit of time
as an indicator of seismic quiescence and activation;
 released seismic energy
E2/3 as an indicator of seismic
quiescence and activation.
released seismic energy
E2/3 as an indicator of seismic
quiescence and activation.
For the territory of Greece, we also used the presence of faults in the spatial scanning cell as a stationary feature. It allowed differentiating the studied area with respect to levels of stationary conditional probability.
The regional earthquake catalogs of Kamchatka and Greece were used without elimination of aftershocks for calculation of maps of expected earthquakes (Table 1). When selecting the range of depths, we stipulated that more than 90% of all earthquakes occurred at these depths. The scope of magnitudes of representative earthquakes was selected from the results of research carried out by Smirnov [1997].
The RTL parameter is the product of three functions: epicentral R, time T, and L accounting for the size of the earthquake source [Sobolev and Tyupkin, 1997]. The RTL values are calculated in the vicinity of the analyzed strong earthquake J characterized by coordinates of epicenter x, y, z, the time of occurrence t, and magnitude M (or the energetic class K ).
The epicentral function R is expressed by the formula
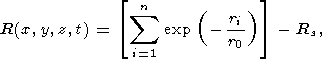 | (1) |
where ri is the epicentral distance from the seismic events, that occurred by the moment tj, to the epicenter of a strong earthquake. The number of these events n is restricted by the experimentally selected time interval Tmax and the radius of the circular area Rmax ; r0 is the coefficient characterizing the degree of attenuation of the influence of seismic events more distant from the epicenter of earthquake J. After calculation of the expression in square brackets, the correction Rs for the trend and periodic (seasonal) variations can be took into account.
The time function T is calculated in a similar way:
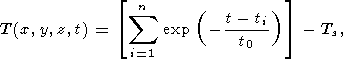 | (2) |
where ti are the times of n seismic events that occurred within Tmax and Rmax. Coefficient t0 characterizes the rate of reduction of the influence of preceding seismic events as they recede into the past from the moment of earthquake J.
The function of focus size L is expressed by
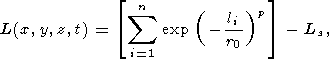 | (3) |
where li is the source size of the earthquakes that occurred before the moment of earthquake J ; these characteristic sizes are calculated by the empirical relation between the length of the rupture source and the energy class. In this paper we use the empirical relation between the length of the rupture and the energy class of the earthquake obtained by Riznichenko [1976]:
If p=1, then the contribution of each of the occurred earthquakes is proportional to the relation of the linear size of the rupture to the epicentral distance. If p=2 and p=3, then it is proportional to the relation of the corresponding areas and volumes respectively. At p =0, all occurred earthquakes produce equal contributions without regard for their size.
The functions R, T and L are dimensionless and are reduced to a single dispersion for their easier application in different combinations. The prognostic parameter RTL was calculated as the product of these three functions. In this case, the seismic quiescence corresponds to the reduced value of the RTL prognostic parameter, whereas the foreshock activation corresponds to its increase.
The earthquake catalogs were used for calculation of the RTL parameter with two essential differences in comparison with MEE method. Firstly, the catalogs were cleaned of aftershocks. Secondly, it was found [Sobolev and Tyupkin, 1997], that the regimes of the more shallow and deeper seismicity in the Pacific seismoactive zone near the coast of Kamchatka significantly differ, while the succession of the stages of seismic quiescence and foreshock activation before strong earthquakes is best manifested by taking account of the seismic events with depths more than 20-30 km. With due consideration of the errors in the determination of the depths, the upper boundary of the hypocenters was chosen equal to 20 km. The choice of the lower boundary had no effect on the results of calculations. It was restricted to 100 km depth for distinctness.
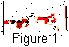 Figure 1 represents a map of expected earthquakes of Kamchatka,
which shows the zones of different levels of conditional probability
P(D1|K ) of occurrence of a strong earthquake
in the
period from 1992 to 1996. The earthquake catalog for 1962-1991 was used
for calculation of this map. The map indicates also the positions of epicenters
of strong earthquakes and of their
aftershocks with
K
Figure 1 represents a map of expected earthquakes of Kamchatka,
which shows the zones of different levels of conditional probability
P(D1|K ) of occurrence of a strong earthquake
in the
period from 1992 to 1996. The earthquake catalog for 1962-1991 was used
for calculation of this map. The map indicates also the positions of epicenters
of strong earthquakes and of their
aftershocks with
K  13.5 (ten events) that occurred in the
forecasting
time interval. Figure 1 implies that the epicenters of nine earthquakes
are located in the zones with conditional probability
P(D1|K)
13.5 (ten events) that occurred in the
forecasting
time interval. Figure 1 implies that the epicenters of nine earthquakes
are located in the zones with conditional probability
P(D1|K)  70%, and
only one earthquake occurred outside these zones.
It should be noted that the latter event that occurred on January 1, 1996,
coincides in place and time with the beginning of the
eruption of Akademiya Nauk Volcano and is probably characterized by
a process of earthquake preparation different from that of the other events.
70%, and
only one earthquake occurred outside these zones.
It should be noted that the latter event that occurred on January 1, 1996,
coincides in place and time with the beginning of the
eruption of Akademiya Nauk Volcano and is probably characterized by
a process of earthquake preparation different from that of the other events.
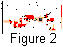 Figure 2 shows a map of expected earthquakes for 1997-2001.
On December 5, 1997, a strong earthquake ( M =7.7) occurred in the
southern part of Kamchatskii Bay. It was accompanied by a
large number of aftershocks, which propagated mainly south-west to
the distance of up to 150 km.
According to the data of different processing centers, the
coordinates
of the epicenter of this earthquake differ by 20-50 km.
For the sake of distinctness, the map in Figure 2 shows the epicenter of
the earthquake, with coordinates 54.8o N and 163.2o E,
and its most strong aftershocks with
M
Figure 2 shows a map of expected earthquakes for 1997-2001.
On December 5, 1997, a strong earthquake ( M =7.7) occurred in the
southern part of Kamchatskii Bay. It was accompanied by a
large number of aftershocks, which propagated mainly south-west to
the distance of up to 150 km.
According to the data of different processing centers, the
coordinates
of the epicenter of this earthquake differ by 20-50 km.
For the sake of distinctness, the map in Figure 2 shows the epicenter of
the earthquake, with coordinates 54.8o N and 163.2o E,
and its most strong aftershocks with
M  6.5.
The Figure 2
implies that the main shock and the area of its aftershocks
was located in the zones with
P(D1|K)
6.5.
The Figure 2
implies that the main shock and the area of its aftershocks
was located in the zones with
P(D1|K) 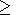 70%.
70%.
The following basic conclusions were formulated on the basis of the retrospective RTL analysis of Kamchatka seismicity [Sobolev and Tyupkin, 1997]. In the interval up to three years, in the area of the source, the stages of seismic quiescence and of foreshock activation consecutively succeed one another, which process is reflected by the RTL anomalies. The most likely period for the occurrence of the predicted earthquake is the time after the return of the RTL anomaly to its normal level, which follows a significant minimum. The linear size of the anomalous area for the earthquake with magnitude 7 is about 100 km, and the instrumental epicenter of the future strong earthquake is located on the edge of the anomalous region.
 As an example, we shall discuss the RTL plots before the three
strong
earthquakes of Kamchatka (Figure 3) of 1992-1993 period:
on March 2, 1992 (52.92o N; 159.89o E; depth of
hypocenter
H =41 km;
M =7.1); on June 8, 1993 (51.25o N; 157.77o E;
H =82 km;
M =7.4), and on November 13, 1993 (51.79o N; 158.83o
E;
H =40 km;
M =7.1). The value of the RTL parameter is
shown in units of the mean square deviation
s calculated from the data
for the whole observation period since 1962. The following values
of the parameters included in formulas (1-3) were used:
r0 =50 km,
t0 =1 year,
Rmax =100 km,
Tmax =2 years,
p=1. One can see from the Figure 3 that all three
earthquakes were preceded by deep minimums indicating the phases
of seismic quiescence. The minimal values were recorded about half
a year prior to the earthquake of March 2, 1992, eight
months before the earthquake of June 8, 1993, and 1.8 year before
the earthquake of November 13, 1993. All three earthquakes occurred
after the time period when the RTL re-established the normal
level of multiyear background (the stage of foreshock activation).
The occurrences of moderate-size
earthquakes ( M =5.0-5.5) in the area of analyzed large earthquakes
were recorded during the anomalous periods before these large events.
As an example, we shall discuss the RTL plots before the three
strong
earthquakes of Kamchatka (Figure 3) of 1992-1993 period:
on March 2, 1992 (52.92o N; 159.89o E; depth of
hypocenter
H =41 km;
M =7.1); on June 8, 1993 (51.25o N; 157.77o E;
H =82 km;
M =7.4), and on November 13, 1993 (51.79o N; 158.83o
E;
H =40 km;
M =7.1). The value of the RTL parameter is
shown in units of the mean square deviation
s calculated from the data
for the whole observation period since 1962. The following values
of the parameters included in formulas (1-3) were used:
r0 =50 km,
t0 =1 year,
Rmax =100 km,
Tmax =2 years,
p=1. One can see from the Figure 3 that all three
earthquakes were preceded by deep minimums indicating the phases
of seismic quiescence. The minimal values were recorded about half
a year prior to the earthquake of March 2, 1992, eight
months before the earthquake of June 8, 1993, and 1.8 year before
the earthquake of November 13, 1993. All three earthquakes occurred
after the time period when the RTL re-established the normal
level of multiyear background (the stage of foreshock activation).
The occurrences of moderate-size
earthquakes ( M =5.0-5.5) in the area of analyzed large earthquakes
were recorded during the anomalous periods before these large events.
In order to evaluate the spatial position of the quiescence zones before the earthquakes with M > 7, the maps of the RTL values were drawn with a net of 15 km range in latitude and longitude. A minimal RTL values that were observed for the period of one year counting back from the time of, correspondingly, the earthquake of March 2, 1992, June 8 and November 13, 1993, were ascribed to all points of the net. An analysis of the summed-up maps resulted in a conclusion that the seismic quiescence region before an earthquake with M > 7 covers an area of about 40 thousand sq. km, and the epicenters of the events are located on the marginal parts of the corresponding anomalies up to 100 km from their centers.
 Since 1996, the Institute of Physics of the Earth of the
Russian
Academy of Sciences receives by e-mail the operative data on the seismicity
of Kamchatka with a lag of a few days. This
information gave us the opportunity for prediction of future events.
In the first half of 1996, two anomalies of the prognostic RTL parameter
were revealed. Their centers were located at the sites
of the Pacific focal zone with coordinates 51.5o N and 158.5o
E
(the southern part of the Avachinskii
Bay) and 56o N, 162.5o E (the Kamchatka
Bay). The RTL plots for
these anomalies are shown in Figure 4 and the location of the seismic
Since 1996, the Institute of Physics of the Earth of the
Russian
Academy of Sciences receives by e-mail the operative data on the seismicity
of Kamchatka with a lag of a few days. This
information gave us the opportunity for prediction of future events.
In the first half of 1996, two anomalies of the prognostic RTL parameter
were revealed. Their centers were located at the sites
of the Pacific focal zone with coordinates 51.5o N and 158.5o
E
(the southern part of the Avachinskii
Bay) and 56o N, 162.5o E (the Kamchatka
Bay). The RTL plots for
these anomalies are shown in Figure 4 and the location of the seismic
 quiescence anomalies is shown in Figure 5. The map displays
minimal values of the RTL parameter in units
s in the 1.07.1995-1.07.1996
interval. Let us discuss the situation in the region of the seismic quiescence
anomaly in the south of Kamchatka (Figure 4a). A strong earthquake
in this area was a serious menace to Petropavlovsk-Kamchatskii. Therefore, on
May 23, 1996, a report was dispatched to the Expert Council for Earthquake
Prediction of the Ministry of Extreme Situations in Russia to the effect that,
in the southern part of Kamchatka, a
seismic quiescence anomaly was developing with the coordinates of the center
51.5o N and 158.5o E.
As a result of an analysis of the previous cases, it was presumed that
in the interval from one month to 1.5 years an earthquake with magnitude
more than 7 can be expected. During this period, a stage
of foreshock activation can develop including earthquakes of the energetic
class more than 11.5. It was also indicated that the instrumental epicenter
of the predicted earthquake usually does not
coincide with the center of the anomaly and is located several tens
of kilometers from it.
quiescence anomalies is shown in Figure 5. The map displays
minimal values of the RTL parameter in units
s in the 1.07.1995-1.07.1996
interval. Let us discuss the situation in the region of the seismic quiescence
anomaly in the south of Kamchatka (Figure 4a). A strong earthquake
in this area was a serious menace to Petropavlovsk-Kamchatskii. Therefore, on
May 23, 1996, a report was dispatched to the Expert Council for Earthquake
Prediction of the Ministry of Extreme Situations in Russia to the effect that,
in the southern part of Kamchatka, a
seismic quiescence anomaly was developing with the coordinates of the center
51.5o N and 158.5o E.
As a result of an analysis of the previous cases, it was presumed that
in the interval from one month to 1.5 years an earthquake with magnitude
more than 7 can be expected. During this period, a stage
of foreshock activation can develop including earthquakes of the energetic
class more than 11.5. It was also indicated that the instrumental epicenter
of the predicted earthquake usually does not
coincide with the center of the anomaly and is located several tens
of kilometers from it.
On June 21, 1996, an earthquake with M =7.1 occurred on the northeastern edge of the anomalous zone, about 80 km from its center (asterisk on the map of Figure 5). The arrows in Figure 4a show the time of the prognostic announcement and of this earthquake. After the earthquake, the RTL plot did not return to the level of the multiyear background. A brief analysis of the present state of seismicity in this region will be given at the end of the paper in the part Discussion.
Let us now to discuss the development of events in the region of the northern anomaly. The stage of seismic quiescence, according to the plot in Figure 4b, began in the middle of 1995 and reached its extreme value by the end of the year. After it, a stage of foreshock activation commenced, and on August 7, 1996, a communication was sent to the Expert Council on Earthquake Prediction of the Ministry for Extreme Situations in Russia to the effect that, in the north of Kamchatka, an anomaly of seismic quiescence appeared with the center at 56o N and 162.5o E, which apparently is the mid-term precursor of an earthquake with magnitude not more than 7. As can be seen in Figure 4b, the anomaly at the moment of the prognostic announcement of August 7, 1996 did not as yet reversed to its zero level, and a year and four months passed before the subsequent strong earthquake of December 5, 1997 occurred. Its magnitude of M =7.7 was higher than that expected from the data of August 7, 1996. The arrows in Figure 4b indicate the time of prognostic announcement and the moment of the earthquake. The position of the instrumental epicenter of the earthquake, shown by an asterisk on the map of Figure 5, is about 120 km from the center of the anomaly.
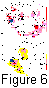 An analysis of the seismic situation in Greece was carried
out on the basis
of experience of joint application of the MEE and RTL algorithms on Kamchatka.
As a result of this joint analysis,
two zones with a higher probability of a strong earthquake occurrence
were suggested (Figure 6). One of these zones is situated east of
the Athens-Thessaloniki line, the other - 200 km to southwest of
the Athens. The maps shown in Figure 6 were handed over to the Greek
scientists at the 29
th General Assembly of the International
Association of Seismology and Physics of the Earth’s Interior
(IASPEI) in August 1997 (Thessaloniki, Greece). On November 18, 1997,
an earthquake of magnitude
M =6.7 (operative data of Geophysical Survey
of Russian Academy of Sciences) occurred in the second revealed zone.
An analysis of the seismic situation in Greece was carried
out on the basis
of experience of joint application of the MEE and RTL algorithms on Kamchatka.
As a result of this joint analysis,
two zones with a higher probability of a strong earthquake occurrence
were suggested (Figure 6). One of these zones is situated east of
the Athens-Thessaloniki line, the other - 200 km to southwest of
the Athens. The maps shown in Figure 6 were handed over to the Greek
scientists at the 29
th General Assembly of the International
Association of Seismology and Physics of the Earth’s Interior
(IASPEI) in August 1997 (Thessaloniki, Greece). On November 18, 1997,
an earthquake of magnitude
M =6.7 (operative data of Geophysical Survey
of Russian Academy of Sciences) occurred in the second revealed zone.
The results of application of the MEE algorithm for retrospective analysis of seismicity of Kamchatka and Greece for the 20-year period demonstrate that the efficiency of earthquakes prediction with magnitude more than M > 5.5 (energetic class K > 13.5) by this method is, on the average, four times greater than random guessing in supposition that the earthquakes obey the Poisson law. MEE algorithm identifies the summed up area of alarm that does not exceed 22% of the area on which at least one earthquake per year occurs. The actual parameters of forecasting of MEE algorithm that were obtained at the prognostic interval of five years for Kamchatka and seven years for Greece are presented in the Table 2.
The application of the RTL prognostic parameter, apparently, may reduce this interval. A restricted as yet experience of prediction of large earthquakes by applying this parameter to five earthquakes retrospectively (three earthquakes in Kamchatka, the Spitak earthquake of 1988 and Umbria earthquake that occurred in Central Italy on September 26, 1997 [Giovambattista and Tyupkin, 1998] and to three earthquakes in real time (two in Kamchatka and one in Greece) shows that the significant anomalies are revealed in the interval up to three years prior to the predicted large earthquake.
Let us briefly outline the present-day situation in the south of Kamchatka in the region of the anomalies, which is shown on the map on Figure 5 and on the plot of Figure 4a. After the earthquake of June 21, 1996 with M =7.1, the RTL plot did not reverse to the level of the multiyear background. The seismic quiescence stage in this region continued when the large earthquake with M =7.7 occurred in the North of Kamchatka on December 5, 1997. A certain analogy can be traced with the course of the process before the earthquakes of 1992-1993 (Figure 3); therefore, the earthquake of June 21, 1996 can be regarded as a foreshock, in a broad sense, of a stronger future earthquake. The development of this anomaly can be complicated by the last stage of preparation of the large earthquake of December 5, 1997. The latter process changed the stress state of the seismoactive zone of Kamchatka, and the earthquake preparation process in the south is either accelerated, or slowed down. It is necessary to continue observation of the anomaly development for intermediate-term prediction.
The strong earthquakes that occurred in Kamchatka on June 21, 1996, M =7.1 and on December 5, 1997, M =7.7, and in Greece on November 18, 1997, M =6.7, confirmed the possibility of prediction "in advance" of future events by using the MEE and RTL methods.
These earthquakes occurred in the 70% probability zones shown on the maps of expected earthquakes. In all cases the predicted earthquakes happened not in the center of the corresponding anomalous areas with characteristic linear size of about 100 km, but on their edges. The earthquake of June 21, 1996 occurred one month after the official prognostic announcement. The earthquake of December 5, 1997 took place 16 months after the official prognostic announcement. The prediction of the future earthquake magnitude by the described methods allows essential errors.
The basic results of the present paper with demonstration of the maps and plots were presented at the 29 th General Assembly of the International Association of Seismology and Physics of the Earth’s Interior (IASPEI) in August 1997 (Thessaloniki, Greece) [Sobolev et al., 1997]. In the present paper these results are supplemented by two strong earthquakes that occurred in 1997, after the Assembly, on November 18 with M =6.7 in Greece and on December 5 with M =7.7 in Kamchatka.
Fedotov, S. A., Energeticheskaya klassifikatciya zemletryasenii i problema magnitud, Nauka, Moscow, 1972 (in Russian).
Gabrielov, A. M., Dmitrieva, O. E., Keilis-Borok, V. I., Kosobokov, V. G., Kuznetsov, I. V., Levshina, T. A., Mirzoev, K. M., Molchan, G. M., Negmatullaev, S. Kh., Pisarenko, V. F., Prozorov, A. G., Reinkhart, Y., Rotvain, I. M., Shebalin, P. N., Shnirman, M. G. and Shreider, S. Yu., Dolgosrochnyi prognoz zemletryaseniy, IFZ AN SSSR, Moscow, 1986 (in Russian).
Giovambattista, R. Di., Tyupkin, Yu. S., RTL prognostic parameter: application to the study of seismicity of Italy, 23-rd General Assembly of European Geophysical Society, Nice, France, Annales Geophysica Part I, Society Symposia, Solid Earth Geophysics & Geodesy, Supplement I to Volume 16, p. C130, 1998.
Kosobokov, V. G., Keilis-Borok, V. I., Localization of intermediate-term earthquake prediction, J. Geophys. Res., 95 (12), 763-772, 1990.
Riznichenko, Yu. V., Razmeri ochaga korovogo zemletryseniya i seismicheskii moment, Riznichenko Yu. V. (Editor), Issledovaniya po fizike zemletryasenii, pp. 9-27, Nauka, Moscow, 1976 (in Russian).
Smirnov, V. B., Opit otcenki predstavitel'nosti dannikh katalogov zemletryasenii, Vulkanologiya i Seismologiya, 4, 93-105, 1997 (in Russian).
Sobolev, G. A. and Koltsov, A. V., Krupnomasshtabnoe modelirovanie podgotovki i predvestnikov zemletryasenii, Nauka, Moscow, 1988 (in Russian).
Sobolev, G. A. and Tyupkin, Yu. S., Low-seismicity precursors of large earthquakes in Kamchatka, Volcanology and seismology, 18, 433-446, 1997.
Sobolev, G. A. and Tyupkin, Yu. S., RTL Prognostic Parameter for Strong Earthquakes, Abstracts of the 29-th General Assembly of the International Association of Seismology and Physics of the Earth’s Interior, August 18-28, p. 143, Geophys. Laboratory of Aristotel Univ., Thessaloniki, Greece, 1997.
Sobolev, G. A., Tyupkin, Yu. S. and Zavyalov, A. D., Map of Expected Earthquakes algorithm and RTL Prognostic Parameter: Joint Application, Abstracts of the 29-th General Assembly of the International Association of Seismology and Physics of the Earth’s Interior, August 18-28, p. 77, Geophys. Laboratory of Aristotel Univ., Thessaloniki, Greece, 1997.
Sobolev, G. A., Chelidze, T. L., Zavyalov, A. D., Slavina, L. B. and Nikoladze, V. E., The maps of expected earthquakes based on a combination of parameters, Tectonophysics, 193, 255-265, 1991.
Wyss, M. and Habermann, R. E., Precursory seismic quiescence, Pure and Appl, Geophys., 126, (2/4), 319-332, 1988.
Zhurkov, S. N., Kineticheskaya konceociya prochnosti tverdikh tel, Vestnik AN SSSR, 3, 46-52, 1968 (in Russian).
Zschau, J., Seismolap: a quantification of seismic quiescence and clustering, Abstracts, Week A, IUGG XXI General Assembly, p. A389, University of Colorado, Boulder, USA, 1995.
 |