Conclusion

We have reviewed thermodynamic properties of geomaterials necessary to study the thermodynamics of the deep interior of the Earth.

(1) In sections 2-5, it was shown that the determination of all the second-order thermodynamic parameters requires knowledge of values of three such parameters. In relation to EOS's, all the thermodynamic parameters were lumped into thermal and caloric types. A summary to finding of EOS's from experimental data was presented. The approaches directly based on measured thermodynamic characteristics can be formulated in the form of partial differential equations. Of 16 third-order thermodynamic parameters, only four (appropriately chosen) are independent. Attention is given to the compilation of a self-consistent database for minerals, relying on input data for a, K_S (or K_T ), ( K_S/ P)_T, (a/ T)_P, ( C_P/ T)_P, and ( K_S/ T)_P.

(2) Each of the eight second-order parameters was analyzed separately, following the plan: the derivation of the identities between their P and T derivatives, the estimation of the intrinsic and extrinsic contributions to the temperature derivatives, useful simplifications of these relations and their consequences, and the explicit approximate dependences of the second-order parameters on pressure and temperature.

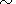(3) In the analysis of thermal expansivity (section 6), the Birch formula for a = a(P) at T (or S ) = constant is generalized. It was shown that a in the lower mantle, calculated by the generalized formula, is sensitive to assumed values of the mixed P-T derivative of the bulk modulus K_T, in the range of dK₀/dT (0-4) 10^-4 K ^-1. The assignment of a value about 2 10^-4 K ^-1 for this derivative gives a in the lower mantle to be close to those by the (exponential) laws of O. Anderson et al. [1993] and Chopelas and Boehler [1992]. Based on these estimates and our analysis, we conclude that the coefficient of thermal expansion decreases along the hot lower-mantle adiabat (from P = 0 to P = 1.35 Mbar) by a factor of 4-5. Considering the O. Anderson power law for a, we stated strict conditions for the consistency of various assumptions regarding the EOS and parameters d_T, K_T, K, and C_V and cleared up the consequencies of these assumptions. In many cases, these conditions are useful for a self-consistent thermodynamic analysis. For example, the power form of the Birch law, K_T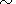 V^b leads to K = constant, K_T = K_T(V), d_T = K = constant, the Murnaghan EOS (41), and for C_V = constant, a = a(V). Various extrapolations of a to high temperatures at P = 0 show a great uncertainty in the resulting thermal expansivity (to 30-50% at T 1500-2000 K), which indicates that high-temperature measurements of a are very neeeded to improve the knowledge of a.

(4) The isobaric specific heat C_P under the lower-mantle conditions (section 7) decreases approximately 10% along the hot adiabat, from P = 0 to P = 1.35 Mbar. At low temperatures T < Q, the intrinsic anharmonicty competely prevails, but at T > Q, when ( C_P/ T)_P is small, its contribution is only 15-30%.

(5) The difference between the thermal pressure model of O. Anderson and the Mie-Grüneisen EOS is emphasized (section 8). This model has two specific features: in general, its thermal pressure is linear in temperature, but the volume dependence of thermal pressure depends on the kind of material. From our estimation, at T > Q, the nonlinear terms in P_th contribute no more than 1-3%. In total, we refer to the existence of, at least, four models of thermal EOS: the Mie-Grüneisen (or more general anharmonic lattice) EOS, a model with various forms of the reference isotherm P(V, T₀) and with a given a(P, T) dependence, the O. Anderson model mentioned above, and the formulation of type (28) with assumed temperature variations of the EOS parameters.

(6) In section 9, the Anderson-Grüneisen parameters d_S and d_T are analyzed in more detail. An explicit expression for d_T(V) at T (or S ) = constant was derived from the generalized formula of Birch. We find that, for dK₀/dT = 2.3 10^-4 K ^-1 (see the derivation of (3)), d_T at the base of the mantle is almost half the value at P = 0.

(7) The adiabatic-isothermal transformation of bulk moduli are discussed in section 10. In addition to the previous considerations, the useful formula (98) was derived for the mixed derivative dK₀/dT. Altogether, this parameter for various geomaterials is estimated by a value of the order of (1-3) 10^-4 K ^-1.

From the analyzed temperature behavior of bulk moduli, we infer that the d_V^T = K - d_T and d_V^S values at room temperature fall mostly between -4 and -1 and between -1 and 1, respectively. However, their high-temperature values are in the range from -1 to 1 for d_V^T and from 0 to 1.5 for d_V^S. The approximation d^T_V 0 ( d_T K and K_T = K_T(V) ) is justified for many but not all minerals.

In relation to the interpretation of seismic tomography data for the lower mantle, we found the following ranges of acceptible value for this largest layer of the Earth: d^T_V 0.2, q 0.8, g 1.1, d_T 3-3.3, and d_S 1.9-2.2 (provided that the thermal interpretation of these data is true).

The K_S values at high temperature, evaluated by the power law with d_S = constant and by the O. Anderson enthalpy method have errors of the order of 2-6 and 1-3%, respectively. Thus, it is confirmed that the O. Anderson [1995] method is quite efficient.

(8) A number of identities for the Grüneisen parameter g and its logarithmic derivative q = ( lng/ ln V)_T were given in section 11. They show that the conditions C_V = constant or C_V = C_V(T) lead to g = g(V) or g = f(V)/C_V(T), respectively. Both these cases are compatible to the O. Anderson thermal pressure model, with t = aK_T = constant or t = t(V). Any of the indicated conditions for C_V also gives q = q(V) or q = constant; moreover, from the inequality 0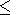 q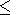 1, it follows that 0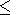 K - d_T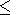 1 and vice versa. Thermodynamically estimated q values fall largely into the interval 0.5-2. This parameter generally decreases with pressure and temperature. In the derivative (g/ T)_P, the intrinsic anharmonicity prevails on the whole, suggesting a significant dependence of g on temperature. In addition to many known expressions for g(V), we derived a new one based on the parameter l 1 - ( ln gT/ ln V)_S 1. The l = 0 case is reduced to the Rice [1965] formula. Variation in l in the interval of 0-1 (accordingly, d_V^S l(1 + agT)^-1 ranges approximately over the same interval for agT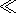 1 ) appreciably affects the g values at high compression.

(9) The identities and approximations for the adiabatic temperature gradient t_S ( T/ P)_S were systematized. Our thermodynamic estimates of the Boehler parameter n = ( lnt_S/ ln V)_T are close to his experimental results for olivine, quartz, and periclase. The uncertainty of the order of one in the estimated n is caused by errors in the used input thermodynamic data. In the derivative (t_S/ T)_P, the intrinsic anharmonic contribution was found to dominate. When determining the EOS from data for t_S, an important role is played by the relation of this parameter to specific heat.

Finally, in sections 6-8 and 10, we checked on the validity of the Mie-Grüneisen EOS used to evaluate a, C_P, t, and K_S. Qualitatively, this EOS model correctly describes the P-T behavior of the indicated parameters, but in general, it does not always provide a sufficiently high accuracy of the estimated values. For this reason (see also the inference (8) above), it is concluded that care must be exercised when applying this type of EOS in geophysics.

Acknowledgments

This document was generated by TeXWeb (Win32, v.1.0) on February 10, 1999.