3. Equations of State and Caloric Functions

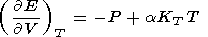
The fundamental equation (1) relates five variables two of which are independent. A simple system can therefore be completely described, given knowledge of its thermal P(V, T) and caloric E(V, T) EOS's. The thermal EOS relates the experimental P-T and theoretical V-T variables and is necessary for transforming these variables in analysis of any thermodynamic property [Zharkov and Kalinin, 1971]. The parameters determined by this EOS kind are termed thermal, whereas the quantities derived either from only the caloric EOS or from both thermal and caloric EOS's are thermed caloric. The latter, in particular, include K_S, g, C_P, and t_S.

The two EOS kinds are related by the equation

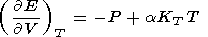(21)

whose integral form is

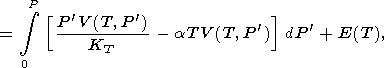where the transformation

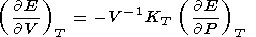is used, the integration constant is

and the integral is taken along an isotherm. In view of (21), the caloric EOS, E(V, T), is completely determined by the given thermal EOS and function E(T) or H(T) at P = 0. It is clear that any of the caloric functions H(T), S(T), G(T), and C_P(T) at P = 0 can used for the same purpose, since the following identities take place

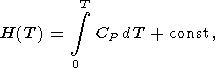(22)

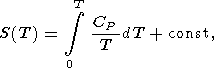(23)

The latter formula can be written in another useful form

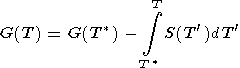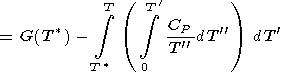(24)

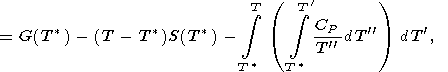where T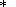 is a fixed temperature.

For a mineral whose composition can be expressed by a sum of oxides (component), the Gibbs energy is formulated in difference terms

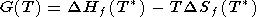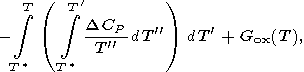(25)

where DH_f = H - H _ox, DS_f = S - S _ox, and DC_P = C_P - C_{P ox} are the differences of enthalpy, entropy and heat capacity between the mineral and oxide sum, respectively (with allowance for the stoichiometric coefficients). Expressions of type (25) are often used in calculating phase equilibria [e.g., Navrotsky and Akaogi, 1984; Kuskov and Galimzyanov, 1986; Kuskov et al., 1989; Fabrichnaya and Kuskov, 1991; Fei and Saxena, 1986; Fei et al., 1990; Sobolev and Babeiko, 1989]. Some authors use an approximation DC_P = 0 (or const 0 ; the functions DC_P(T) are sometimes found from empirical formulas of type (67)). In any case, the term DH_f(T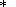) in (25) implicitly contains an arbitrary normalizing constant [Kalinin et al., 1991].

Integrating (3) gives

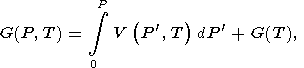(26)

where G(T) = G(T, 0) is defined by (24) or (25) and can be written in the reduced form

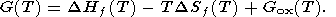(27)

Methods for determining EOS's in geophysics can be classified as follows.

(1) The macroscopic approach suggested by Murnaghan [1951] and Birch [1952] gives the volume dependence of pressure at T (or S ) = const in the form [Ullmann and Pankov, 1976]

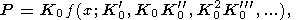(28)

Hereafter, the values with the subscript 0, unless otherwise specified, are taken at P = 0 and an arbitrary temperature, the moduli K₀ K_T0, K₀ = ( K_T/ P)_T0,... are material parameters, and x = V/V₀ = r₀/r is the compression ratio parameter. Most data for the material parameter values were obtained at room temperature [e.g., Sumino and O. Anderson, 1984]. Among the last experimental achievements are ultrasonic measurements at high pressures [e.g., Fujisawa, 1987; Webb, 1989; Yoneda, 1990; Liebermann et al., 1993], X -ray data of high pressures and high temperatures [e.g., Yagi et al., 1987; Mao et al., 1991; Fei et al., 1992a, 1992b; Boehler et al., 1989], spectoscopic observations of minerals [e.g., Chopelas, 1990a, 1990b, 1991a, 1991b, 1993; Hofmeister, 1987, 1991a], and high-temperature P=0 measurements of elastic constants by the rectangular parallelepiped technique [O. Anderson et al., 1992a; O. Anderson, 1995].

An explicit form of function f in (28) (the volume dependence of pressure) was considered by Murnaghan [1951], Birch [1952, 1968, 1978, 1986] and others [Thomsen, 1970, 1971; Ahrens and Thomsen, 1972; Davies, 1973; Ullmann and Pankov, 1976, 1980; Pankov and Ullmann, 1979a; Stacey, 1981; Aidun et al., 1984; Jeanloz, 1989; Bina and Helffrich, 1992; Isaak et al., 1992; Wall et al., 1993]. The most widely used equation of this type is the Birch-Murnaghan EOS.

Elastic moduli and sound velocities in minerals depends first of all on the composition, crystalline structure, pressure, and temperature. Data on these dependences are generalyzed and interpreted in terms of empirical laws such as the Birch's law, the seismic EOS, the law of corresponding states, and a universal EOS [Birch, 1961; O. Anderson and Nafe, 1965; D. Anderson, 1967, 1987; Chung, 1973; Davies, 1976; O. Anderson, 1973; D. Anderson and O. Anderson, 1970; Mao, 1974; Kalinin, 1972; Schankland and Chung, 1974; Campbell and Heinz, 1992]. These laws enable us to estimate the parameters K₀ and, to a lesser accuracy, K₀ for unmeasured minerals [D. Anderson, 1988; Duffy and D. Anderson, 1989].

(2) Statistical physics describing the vibrations of atoms in crystals provides the background for microscopic EOS theory including the Mie-Grüneisen EOS [Grüneisen, 1926; Born and Huang, 1954; Leibfried and Ludwig, 1961; Knopoff, 1963; Knopoff and Shapiro, 1969; Zharkov and Kalinin, 1971; Wallace, 1972; Mulargia, 1977; Mulargia and Boschi, 1980; Hardy, 1980; O. Andrrson, 1980; Gillet et al., 1989, 1990, 1991; Richet et al., 1992; Reynard et al., 1992]. This approach also uses the lattice or vibrational Grüneisen parameters, as well as either semiempirical potentials of atomic interactions or the reference (isothermal or adiabatic) P-V relations derived from continuum mechanics [e.g., Al'tshuler, 1965; Zharkov and Kalinin, 1971; Ahrens and Thomsen, 1972; McQueen, 1991]. The material parameters in these cases are determined using static and dynamic compression data, elastic constant measurements, caloric functions, and vibrational spectrums.

(3) Integrating (12) yields the pressure as a sum of two terms: a reference isotherm and the thermal pressure increment DP_th. This thermodynamic approach based on experimental data has been developed by O. Anderson [1979a, 1979b, 1979c, 1980, 1982, 1984, 1988, 1995] and was used to describe the X -ray and resonance data for a set of minerals [O. Anderson et al., 1982, 1992a; O. Anderson and Yamamoto, 1987; O. Anderson and Zou, 1989; Mao et al., 1991; Fei et al., 1992a, 1992b].

(4) More intricate theoretical EOS models are derived from ab initio calculation using the Hartree-Fock and Thomas-Fermi-Dirak methods, as well as pseudopotential theory, many-term contributions in semiempirical potentials, and molecular dynamics [Hemley et al., 1985, 1987; Isaak et al., 1990; Wolf and Bukowincki, 1987, 1988; Wall and Price, 1988; Wall et al., 1986; D'Arco et al., 1991; Price et al., 1989; Matsui et al., 1987; Matsui, 1988, 1989; Reynard and Price, 1990; Agnon and Bukowinski, 1990a; Walzer, 1992; Cohen, 1987a; Dovesi et al., 1987; Catlow and Price, 1990; Boisen and Gibbs, 1993; Silvi et al., 1993; Catti et al., 1993; Barton and Stacey, 1985].

As mentioned above, the complete description of a simple system requires knowledge of either any of its thermodynamic potentials or its thermal EOS and one of the caloric functions (at P = 0 ). Table 1 lists various approaches to the determination of EOS's, showing which functions must be found from theory or experiment so as to provide such a complete description. These approaches can also be formulated in the form of partial differential equations with appropriately chosen boundary conditions.

4. Thermodynamic Parameters of the Third and Higher Orders

The order of a thermodynamic parameter (characteristic of a matter) is defined by the maximum order of the thermodynamic potential derivative involved to define the thermodynamic parameter. To find all of the third-order parameters ( P, V, T, or S derivatives of the second-order parameters), whose total number for the potentials in (1)-(4) is 16, it is sufficient to know four independent and appropriately chosen third-order parameters, in addition to knowledge of the lower-order parameters. Specifically, experiments often provide information on the derivatives ( K_S/ P)_T (or

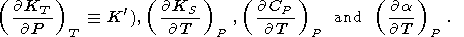The relationships of these derivatives to other parameters are further discussed in later sections.

To extrapolate data on thermodynamic properties to high pressures and temperatures, the power volume dependence is often applied stating that the logarithmic volume derivative of the parameter considered is a constant [Zharkov, 1986; D. Anderson, 1988, 1989]. The temperature derivative of any parameter A at P = const is represented in the dimensionless form

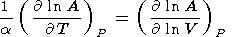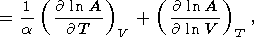(29)

where the first term characterizes the so-called intrinsic anharmonicity and the second is a parameter of the extrinsic anharmonicity related to thermal expansion [Jones, 1976; Smith and Cain, 1980]. Parameter A can be any physical property, such as the transport coefficients or mode Grüneisen parameters [Reynard et al., 1992; Gillet et al., 1989].

5. Thermodynamic Database

The database on properties of minerals, required for geophysical analysis and EOS construction, must include first of all their density and the second and third order thermodynamic parameters. An example of such database for three mantle minerals is given in Tables 2 and 3, and the database for 25 mantle minerals, including their high-pressure phases (and some fictive phases), is presented in Internet [Pankov et al., 1997]. The parameter values in these tables refer to the conditions P = 0, T = 300 K or P = 0 and the temperature indicated. Apart from the second-order thermodynamic parameters, Table 2 includes the molar mass M, mean atomic weight m, density r, the melting temperature T_m, the Debye temperatures Q ( Q_a is the acoustic temperature, Q_a is from fitting the Mie-Grüneisen EOS to data on a [Suzuki, 1975a, 1975b], and Q_th is our estimate from data on specific heat), the classical value C_V = 3R/_m ( R is the gas constant), the enthalpy DH_f and entropy DS_f of mineral formation from oxides, and the estimated thermal pressure P_th 0.5aK_T. It is important to have mutually consistent values of the second (and higher) order parameters: here, the calculations are based on the input values of K_S (or K_T ), a, and C_P. At high temperatures, T > 300 K, the a and C_P values were found by the empirical formulas from Fei and Saxena [1987] and Fei et al. [1990, 1991], and for K_S, we give either experimental values or our estimates through the Anderson-Grüneisen parameter d_S (at 300 K), which is assumed to be a constant (see Table 3 and sections 9 and 10). The values listed in Table 3 are based on the input values of the derivatives ( K_S/ P)_T, ( K_S/ T)_P (or d_S ), ( C_P/ T)_P, and a = a^-2 (a/ T)_P, as well as on the second-order parameter values given in Table 2. The high-temperature values of the third-order parameters were evaluated using the condition ( K_S/ P)_T const. Finally, in Table 2 are given the references to sources of thermodynamic data for each of the minerals.

This document was generated by TeXWeb (Win32, v.1.0) on February 10, 1999.