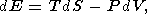
Thermodynamically, the Earth is a heat engine described by a variety of parameters that can be determined from equations of state (EOS) and models of condensed media. A great progress has been achieved in the development of such models [e.g., Jeanloz, 1983; Hemley et al., 1985, 1987; Wall et al., 1986; Catti, 1986; Cohen, 1987a, 1987b; Dovesi et al., 1987; Wolf and Bukowinski, 1987, 1988; Wall and Price, 1988; Matsui et al., 1987; Matsui, 1988, 1989; Price et al., 1989; Catlow and Price, 1990; Isaak et al., 1990; Reynard and Price, 1990; Agnon and Bukowinski, 1990a; Matsui and Price, 1991; D'Arco et al., 1991; Walzer, 1992; Silvi et al., 1993; Catti et al., 1993; Boison and Gibbs, 1993]. Nevertheless, practical studies in geophysics are based, to a large extent, on the use of semi-empirical EOS's [Birch, 1952, 1986; O. Anderson, 1966b, 1995; Pankov and Ullmann, 1979a, 1979b; D. Anderson, 1967, 1987, 1989; Stacey, 1981; Leliva-Kopystynski, 1991; Bina and Helffrich, 1992; Wall et al., 1993]. The properties of geomaterials directly determined from laboratory measurements at high pressures and temperatures are necessary for solving many geophysical problems and provide important constraints on the EOS structure.
Since the fundamental paper of Birch [1952], a great deal of information has been accumulated on the properties of geomaterials and their geophysical implication [e.g., Stacey, 1977a, 1977b, 1992, 1994; Jeanloz and Thompson, 1983; Brown and Shankland, 1981; Zharkov and Kalinin, 1971; Zharkov, 1986; Jeanloz and Knittle, 1989; O. Anderson et al., 1992a, 1992b; 1993; Kuskov and Panferov, 1991; D. Anderson, 1989; O. Anderson, 1988, 1995].
This paper is devoted to the review of relationships between the basic thermodynamic characteristics and of their variation with pressure and temperature. First, we deal with eight parameters of the second order. We emphasize their self-consistent determination and the relations to EOS's and give a summary of approaches used to find the empirically based EOS's. An example of the thermodynamically consistent database for mantle minerals is presented. Then, each of the second-order parameters is treated separately: the identities involving their P-T derivatives (third-order parameters) are established and practically useful approximations are analyzed, including some explicit P-T dependences of the second-order parameters. Some estimates for the fourth-order parameters are also given. The relations between various quantities are represented in the form convenient for practical use of experimental data and for theoretical analysis. Finally, a number of estimates are given for the low-mantle properties. Our analysis serves as an addition to the reviews of O. Anderson [1995] and Stacey [1994].
In classical thermodynamics, simple systems experiencing reversable changes of state are described by a variety of parameters including the hydrostatic pressure P, temperature T, volume V (or density r ), and entropy S. The starting point of thermodynamic analysis is the standard expresions for the total thermodynamic differentials [e.g., Callen, 1960; Morse, 1969; Kelly, 1973]
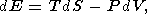 | (1) |
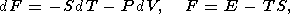 | (2) |
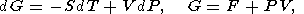 | (3) |
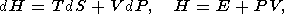 | (4) |
where E is the internal energy, F is the free energy (Helmholtz potential), G is the free enthalpy (Gibbs potential), and H is the enthalpy.
Eight second-order parameters are largely used in geophysics: the volume coefficient of thermal expansion a, the isobaric CP and isochoric CV heat capacities, the isothermal KT and adiabatic KS bulk moduli, the thermal pressure coefficient t, and the adiabatic pressure derivative of temperature (adiabatic temperature gradient in pressure) tS. The respective definitions of these parameters are
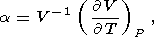 | (5) |
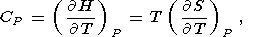 |
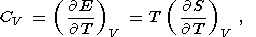 | (6) |
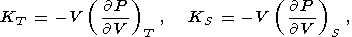 | (7) |
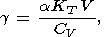 | (8) |
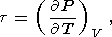 | (9) |
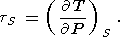 | (10) |
By equating the cross derivatives of the four thermodynamic potentials, we obtain the Maxwell relations [see, e.g., Stacey, 1977a]
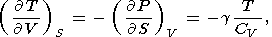 | (11) |
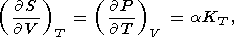 | (12) |
 | (13) |
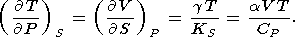 | (14) |
Moreover, it is easily shown that the second derivative of each of these potentials can be expressed in terms of the above parameters or coefficients; i.e., we may write the matrix
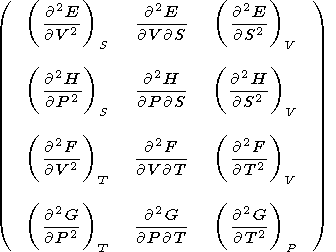 |
| (15) |
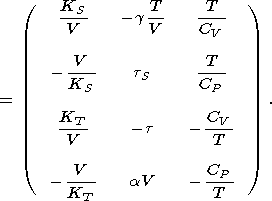 |
The number of independent second-order parameters is obviously three, and consequently, the eight second-order parameters introduced above must satisfy five relations. Four of them are (11)-(14), and the fifth can be derived by changing from one pair of characteristic variables to another; specifically,
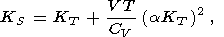 | (16) |
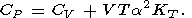 | (17) |
Thus, if the parameters a, CP, and KS (or KT ), as it usually is, are determined experimentally, then the remaining five parameters can be found from the identities
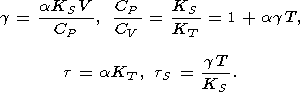 | (18) |
We recall two examples of using the thermodynamic relations in geophysics. The first concerns the Williamson-Adams-Birch equation for the density gradient within the Earth [Birch, 1952; D. Anderson, 1989]. We quote this equation in the form
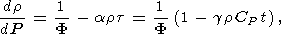 | (19) |
where r and P are the density and pressure in the Earth's interior, respectively, F = KS/r is the seismic parameter, and t = dT/dP - tS is the superadiabatic temperature gradient. Equation (19) is easily obtained from
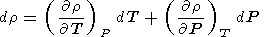 |
with reference to (5), (16) and (14) or (18).
Another example is the adiabatic temperature gradient in depth l within the Earth (see (14)) [e.g., Quareni and Mulargia, 1989]
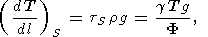 | (20) |
where g is the gravitational acceleration, and furthermore, the mechanical equalibrium equation dP/dl= rg is used.
According to the PREM model [D. Anderson, 1989], F = 50, 80, and 117 km 2 /s 2 at l = 400, 1071, and 2740 km, respectively. Assuming that g = 1-1.5 and T = 1700, 2200, and 3000 K sequently at the indicated depths [D. Anderson, 1989; Pankov, 1989], (20) yields (dT/dl)S = 0.3-0.5 K/km, the value usually cited in geophysical literature.