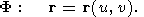
Свойства поверхностей изучаются в курсе дифференциальной геометрии (см., например, [Погорелов, 1969; Постников, 1979; Thorpe, 1979]). Поверхность - это образ двумерного открытого множества W, точками которого являются числа u и v, в трехмерное евклидово пространство E. Отображение задается векторнозначной функцией
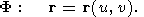 | (П1.1) |
Параметры u и v называют криволинейными координатами на поверхности. Отношение их приращений du/dv определяет некоторое направление на поверхности F.
В настоящей работе рассматриваются лишь гладкие отображения (П1.1). Поверхность F в (П1.1) называется регулярной поверхностью, если для любой точки (u, v) векторы
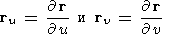 | (П1.2) |
являются линейно независимыми. Поверхность (П1.1) имеет в каждой точке
единственную касательную плоскость, определяемую единичным вектором
нормали
На основе дифференциала вектора (П1.1)
записывается первая квадратичная форма поверхности
I, определяемая как
скалярное произведение вектора
d r на себя
Форма
I задает метрику поверхности: через нее выражаются длины дуг на
поверхности, углы между кривыми на поверхности, площади на поверхности и т.д.
Вторая квадратичная форма поверхности
II зависит от изменения вектора
единичной нормали
и определяется как
Значения первой и второй квадратичных форм зависят в каждой точке от
выбранного направления
du/dv.
Важные свойства поверхности задаются характеристиками ее кривизны. В
конечном счете понятие кривизны поверхности восходит к понятию кривизны
кривой, которая определяется как предел отношения угла между касательными в
точках
А и
В кривой к длине отрезка дуги
АВ при стремлении длины отрезка к
нулю. Нормальная кривизна поверхности в данном направлении
du/dv с точностью
до знака равна кривизне кривой, которая получается в сечении поверхности с
плоскостью, перпендикулярной касательной плоскости и содержащей данное
направление
du/dv. В дифференциальной геометрии установлено, что нормальная
кривизна поверхности в некотором направлении
du/dv равна отношению
квадратичных форм
II/I, вычисленному для этого направления. Таким образом,
каждая точка поверхности характеризуется бесконечным множеством нормальных
кривизн.
В каждой точке поверхности существует два взаимно-перпендикулярных
направления (1) и (2), при дифференцировании по которым приращение
d n вектора нормали пропорционально приращению
d r
Эти направления называются главными, а соответствующие коэффициенты
пропорциональности
K1 и
K2 в (П1.7) называются главными кривизнами. В шаровой
точке ( K1=K2 ) и в точке уплощения ( K1=K2=0 ) любое направление является
главным. Главные кривизны совпадают с экстремальными значениями множества
нормальных кривизн поверхности в данной точке. Полусумма главных кривизн
называется главной кривизной поверхности, а их произведение
определяет гауссову (полную) кривизну. Модуль полуразности главных кривизн
мы называем интенсивностью кривизны. Существует следующая классификация
точек поверхности: точка является
Главные кривизны
K1 и
K2 являются корнями квадратного уравнения
коэффициенты которого выражаются через коэффициенты первой (П1.4) и второй
(П1.6) квадратичных форм. Если поверхность задана в декартовой системе
координат
x, y, z уравнением
то коэффициенты квадратичных форм вычисляются по формулам
В случае пологой поверхности, когда квадратами первых производных от функции
w(x, y) можно пренебречь по сравнению с единицей, приведенные
формулы для
расчета главных кривизн совпадают с формулами для нахождения собственных
значений тензора кривизны-кручения
Пусть
F1 и
F2 - регулярные поверхности. Топологическое
отображение
F1 на
F2 называется конформным, если оно
сохраняет
углы между кривыми в том смысле, что соответствующие кривые на этих поверхностях
пересекаются под одинаковыми углами. Для конформности отображения
F1 на
F2 необходимо и достаточно пропорциональности
их первых квадратичных
форм (при соответствующей параметризации и при сопоставлении точек с
одинаковыми координатами).
Поверхности
F1 и
F2 называются изометричными, если существует
взаимно-однозначное отображение
F1 на
F2, при котором
соответствующие кривые на этих поверхностях имеют одинаковые длины.
Если регулярные поверхности
F1 и
F2 можно параметризовать так,
что их первые квадратичные формы будут совпадать, то поверхности изометричны.
Обратно, если поверхности
F1 и
F2 изометричны, то
они могут быть параметризованы так, что их первые квадратичные формы будут
одинаковыми.
Отображение одной поверхности на другую называется эквиареальным, если
соответствующие при этом отображении области имеют одинаковую площадь.
При изометричном отображении сохраняются углы между кривыми и
площади (т.е. изометричное отображение является одновременно конформным и
эквиареальным). Обратное также верно: если отображение одной поверхности на
другую конформно и эквиареально, то оно изометрично. Представив поверхность
выполненной из гибкого, но нерастяжимого материала и произвольно изгибая ее,
мы не изменим длин лежащих на них кривых и, следовательно, получим
изометричную поверхность. Основываясь на этом, математики XIX века стали
называть изометрии изгибаниями.
Согласно теореме Гаусса (theorema egrerium) гауссова кривизна
H поверхности не меняется при изгибаниях (изометриях), т.е. изометричные
поверхности в соответствующих друг другу точках имеют одинаковую гауссову
кривизну. Отсюда, в частности, следует, что никакую сколь угодно малую часть
сферы нельзя изогнуть на плоскость. Изометрично изгибаемые (развертывающиеся)
на плоскость поверхности должны обладать нулевой, полной кривизной. Хорошо
известными примерами развертывающихся поверхностей являются цилиндр и
конус, принадлежащих к так называемому классу линейчатых поверхностей.
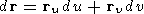
(П1.3) 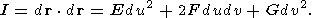
(П1.4) 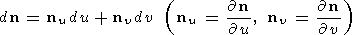
(П1.5) 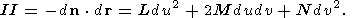
(П1.6) 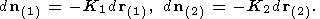
(П1.7) 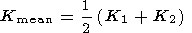
(П1.8) 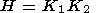
(П1.9) 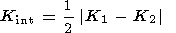
(П1.10)
Классификация основана на типе параболоида, соприкасающегося с поверхностью
в данной точке. Если все точки поверхности являются точками одного типа, то в
тексте настоящей работы иногда название типа точки переносится на поверхность,
т.е. поверхность может быть названа параболической, эллиптической или
гиперболической.
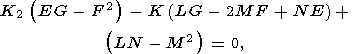
(П1.11) 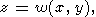
(П1.12) 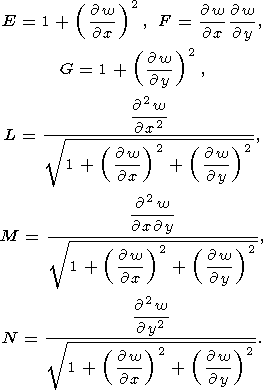
(П1.13) 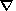
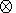
 w.
В тексте настоящей работы максимальная из главных кривизн обозначается через
Kmax, а минимальная - через
Kmin.
w.
В тексте настоящей работы максимальная из главных кривизн обозначается через
Kmax, а минимальная - через
Kmin. Приложение 2
Отображение поверхностей
This document was generated by TeXWeb
(Win32, v.1.0) on April 30, 2000.